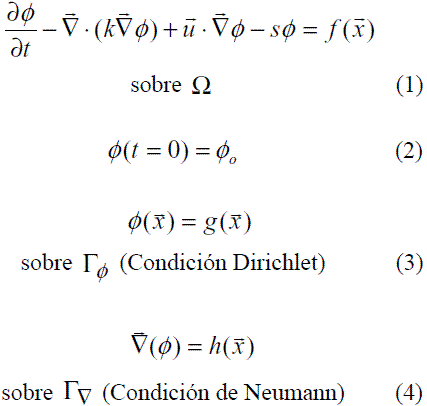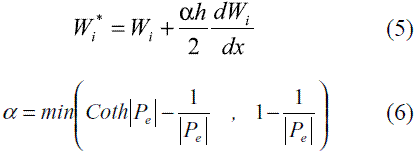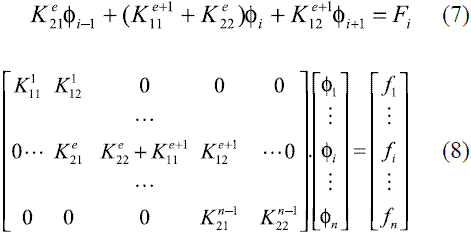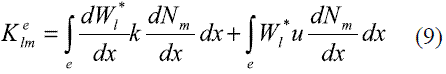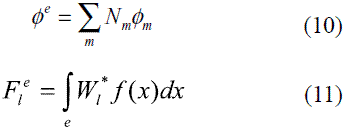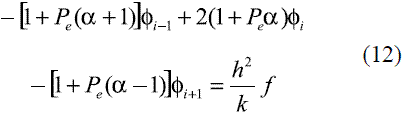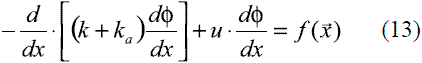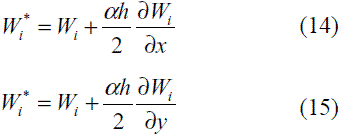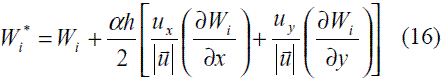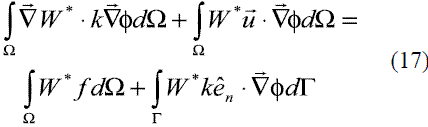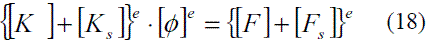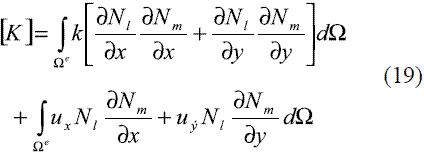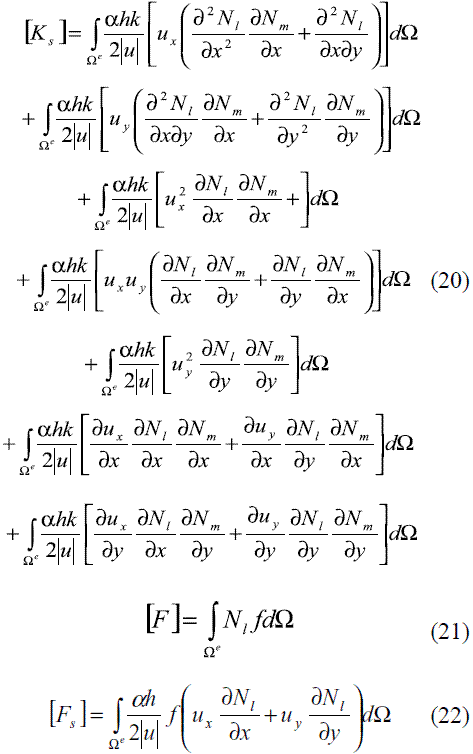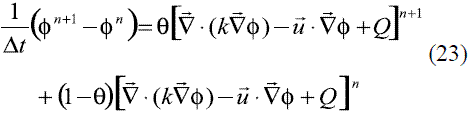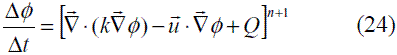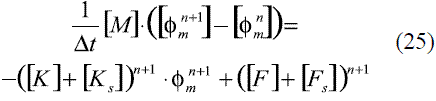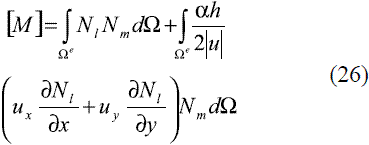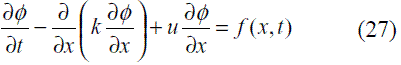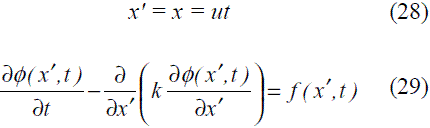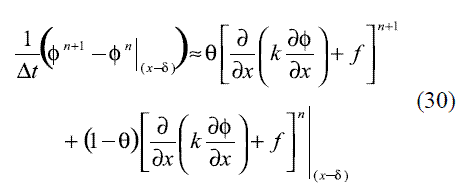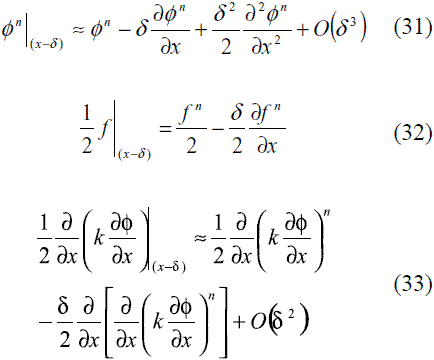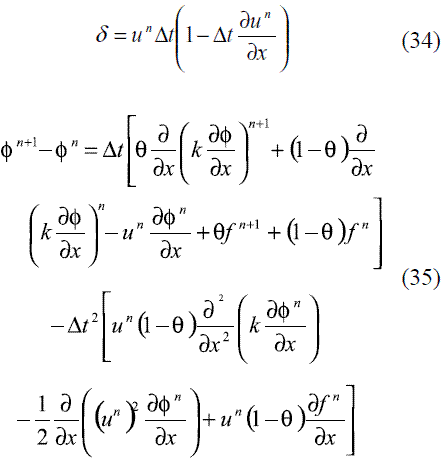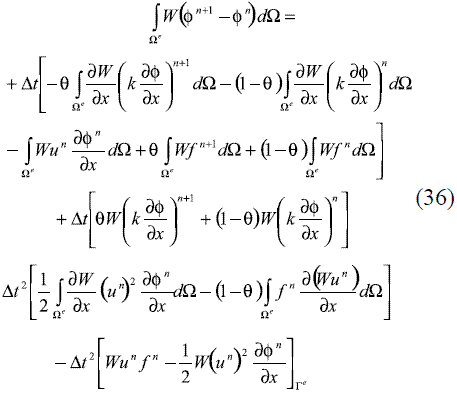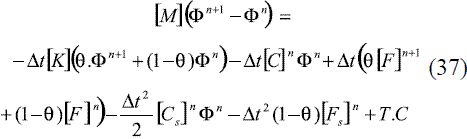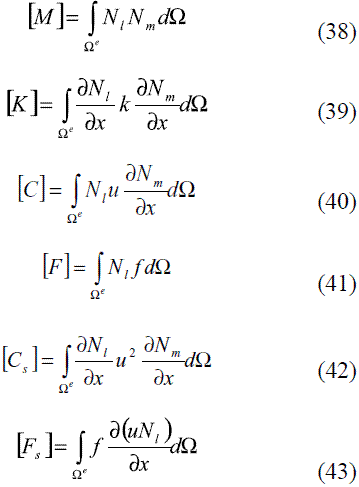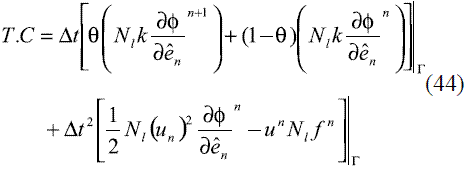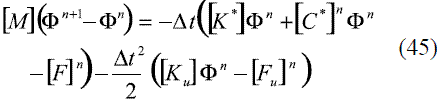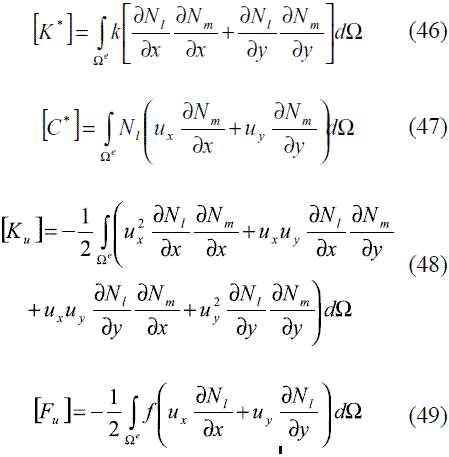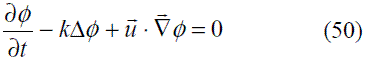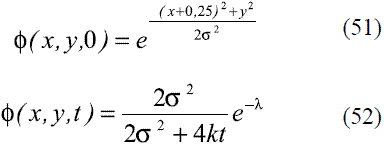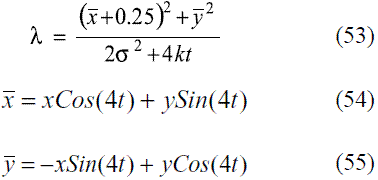Comparación del método de líneas características y el método Petrov Galerkin en contracorriente para problemas de advección dominante

A comparison between characteristic lines and streamline upwind Petrov-Galerkin method for advection dominated problems

Carlos Humberto Galeano, Diego Alexander Garzón^*, Juan Miguel Mantilla

Universidad Nacional de Colombia, Kr. 30 N^o 45-03, Edificio 453 Oficina 401, Bogotá, Colombia.

 

---

Resumen

El presente artículo desarrolla numéricamente el problema de la ecuación diferencial de difusión-advección, empleando el método de Galerkin sobre líneas características y el método de Petrov-Galerkin en contracorriente (SUPG). Las condiciones dominantemente advectivas en el problema solucionado, mostraron que para casos con números de Peclet muy elevados, el método de las líneas características no logra una estabilización de la solución, tal como lo hace el método SUPG. No obstante, para valores pequeños en el número de Peclet, el método de líneas alcaza aproximaciones estabilizadas y errores totales en norma de energía ligeramente menores a los del método SUPG. Las gráficas de convergencia trazadas mostraron que el comportamiento del error en norma L² de la solución convencional por elementos finitos o Bubnov-Galerkin, es muy similar al del error encontrado con el método de las líneas características.

Palabras clave: Petrov-Galerkin, líneas características, SUPG, advección, difusión

 

---

Abstract

This article develops numerically the advection-diffusion equation problem, using Galerkin on characteristic lines and Streamline Upwind Petrov- Galerkin (SUPG) methods. The dominated advective conditions in the solved problem showed that for cases where high Peclet numbers are encountered, characteristic lines don’t achieve a stable solution, as SUPG does. Nevertheless, for low Peclet numbers, characteristic lines achieve stabilized results and total energy norm errors slightly lower to SUPG’s. Convergence figures depicts that L² energy norm error in the solution by finite elements or Bubnov-Galerkin, is very similar to the error found with characteristic lines method.

Keywords: Petrov-Galerkin, characteristic lines, SUPG, advection, diffusion

 

---

Introducción

Muchos problemas de la física, la química, la economía, la biología, la bioingeniería, e incluso la ecología, entre otros campos, pueden ser modelados a través del balance de tres fenómenos: la difusión, la advección y la reacción. Dicho balance se plantea en la ecuación diferencial de difusión-advección-reacción (1) [1], junto con las condiciones iniciales y de contorno e descritas en (2), (3) y (4).

En las anteriores ecuaciones φ es la función escalar (o vectorial) a encontrar, k≥0 es el coeficiente difusivo, 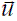es el campo de velocidad asociado al proceso advectivo, s es el coeficiente fuente (s>0) implica producción y (s<0) significa disipación), f (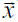) es la función de generación, g(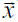) es la función que define el valor del campo escalar φ sobre la frontera 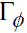y h(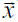) es la función que define el valor del flujo sobre la frontera 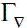[1].

Algunas de las ecuaciones específicas obtenidas a partir de la simplificación de la expresión (1) son:

Ecuación de Helmholtz: empleada en los problemas de acústica, electromagnetismo y sismología. Esta expresión se obtiene considerando un término de producción positivo (s>0) y eliminando el término advectivo ( 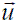= 0) [2].

Ecuación de Difusión-Reacción (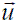 = 0 ): la cual tiene múltiples aplicaciones, como por ejemplo en problemas de morfogénesis [3], crecimiento de tumores [4, 5], formación de tejidos [6], bioquímica [7, 8, 9], dinámica de población [10], astrofísica [11], entre otras.

Ecuación de Difusión-Advección (s=0): utilizada ampliamente en problemas de dispersión de gases contaminantes (sin reacción, especialmente en dispersión de productos de la combustión altamente estables) [12].

Ecuación de Advección-Reacción (k=0): usada en el modelado de dispersión de contaminantes acuíferos en aguas con alta velocidad.

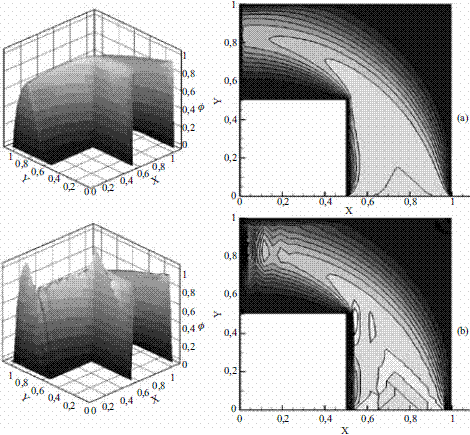
Además de la enorme utilidad de la expresión (1) para el estudio de fenómenos de tan diversa naturaleza, como la economía [13], la genética [14] y la propagación de incendios [15], solo por nombrar algunos campos, ciertas formas de esta ecuación se caracterizan por la dificultad en la implementación de soluciones numéricas y el requerimiento de técnicas especiales para construir una aproximación [16, 17]. En numerosos casos las soluciones numéricas que se han implementado para el desarrollo de este tipo de ecuaciones presentan oscilaciones falsas que no se ajustan al comportamiento real del fenómeno modelado [18] (Figura 1). En efecto, aunque la formulación convencional de elementos finitos, o método de Bubnov-Galerkin, resulta útil y adecuada para el tratamiento de muchos problemas de la ingeniería, especialmente en el campo de la mecánica de sólidos [19], presenta problemas de estabilidad cuando en la ecuación diferencial aparecen operadores no autoadjuntos, tal como el término advectivo en la ecuación (1) [18]. Este término advectivo, bajo la formulación convencional (Bubnov- Galerkin), tiene un efecto desestabilizador de la matriz de rigidez, introduciendo asimetría en la misma y produciendo oscilaciones falsas en la aproximación que se llega a alcanzar, tal como se muestra en la figura 1.

Figura 1 Solución numérica estabilizada (a) y no estabilizada (b) del problema de Brezzi [20]

La eliminación de estas oscilaciones o estabilización de la solución, se logra regresando el carácter simétrico a la matriz de rigidez, lo cual puede ser alcanzado empleando diversos métodos, entre los cuales se puede citar: el método de las líneas de características [21, 18], el método de cálculo finito [22], el método de paso fraccional θ [23], el método de mínimos cuadrados de Galerkin [24] y el método Petrov- Galerkin de contracorriente [25].

Este artículo presenta un estudio comparativo de dos técnicas numéricas empleadas para estabilizar la solución por elementos finitos de la ecuación de difusión-advección-reacción: el método Petrov-Galerkin en contracorriente o SUPG (del inglés Streamline Upwind Petrov-Galerkin) y el método de las líneas características de Galerkin (MLC). En la primera parte del texto se presenta el fundamento matemático de cada una de las técnicas a evaluar, mientras que en una segunda parte se presentan los resultados obtenidos, tanto con SUPG como con MLC, en el desarrollo de dos casos de estudio que involucran condiciones de advección dominante. Posteriormente se analizan los resultados y se presentan las conclusiones.

Metodología

El método de estabilización de Petrov- Galerkin en contracorriente (SUPG)

El SUPG se basa en la estabilización de la matriz de rigidez empleando funciones de ponderación modificadas, de modo que se otorgue un mayor peso a la información de los nodos ubicados aguas arriba [18]. Este método de estabilización, planteado por primera vez por Zienkiewicz [25], fue usado formalmente por Christie [26] y Zienkiewicz [27], y generalizado como técnica para problemas de advección dominante por Hughes [28]. A partir de este punto, han aparecido diversas variantes alrededor del método, como las planteadas por Hughes [29], Baiocchi [30], Harari [31], Russo [32], Cockburn [33] y Araya [34], entre muchos otros trabajos.

En problemas unidimensionales la estabilización con el método de Petov-Galerkin puede ser alcanzada adicionando un término perturbador a la función de peso estándar (W_i), tal como se muestra en (5) [18], en donde h es el tamaño característico del elemento y a es un parámetro de perturbación positivo calculado por medio de la expresión (6) [26].

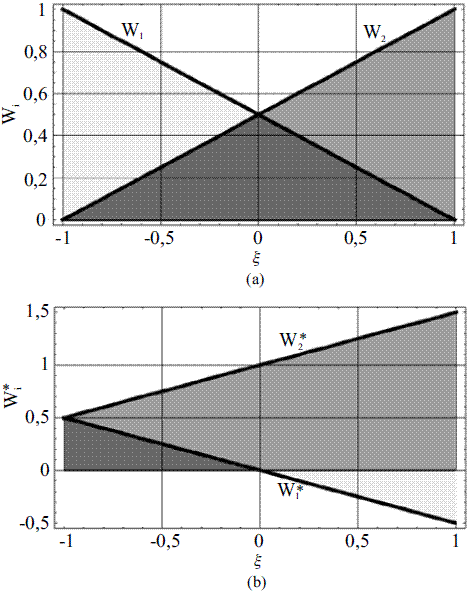
En esta última expresión, en la cual Pe es el número adimensional de Peclet definido como 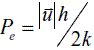, se observa que la función de peso solo debe ser perturbada si Pe>1. En otras palabras, para valores inferiores a la unidad en el número de Peclet, la formulación SUPG lleva al planteamiento convencional de Bubnov-Galerkin. El término adicionado a la función de peso original W_i en (5), modifica las funciones de ponderación W_i^*, tal como lo muestra la figura 2, reduciendo el área bajo la curva de la función de peso W_i, al mismo tiempo que se aumenta el valor de la integral de W₂ a lo largo del elemento. Esta modificación sobre wi logra sobrestimar el valor de los coeficientes K₂₁ por encima de los coeficientes K₁₂, en la ecuación de ensamble (7) de un nodo interno i, la cual es obtenida a partir del sistema de ecuaciones (8). Esta sobre estimación de los términos K₂₁ logra mejorar el carácter simétrico de la matriz de rigidez y dar una estabilidad al método.

Para una ecuación de difusión-advección, los términos de la matriz de rigidez [K] de un elemento e, calculados de acuerdo con el método SUPG unidimensional, están definidos por medio de la expresión (9) [18].

Figura 2 Funciones de peso originales (a) y perturbadas de acuerdo con el método SUPG (b)

En esta última expresión N_m son funciones de forma empleadas en una aproximación por tramos convencional, como la planteada en (10). De forma análoga, los términos del vector [F] para un elemento e se definen de acuerdo con (11) [18].

El uso de las expresiones (9) y (11), en la ecuación (7), permite llegar a la ecuación de ensamble estabilizada (12) [18].

Se puede verificar fácilmente como la ecuación de ensamble unidimensional (12), obtenida empleando la estabilización SUPG, puede ser construida de otra forma, partiendo de un planteamiento Bubnov-Galerkin y aumentando artificialmente el término difusivo, tal como se plantea en (13) [18].

donde k_a es el término de difusivo artificial incluido para estabilizar la solución y el cual se define como k_a =^1/2 auh. Esta interpretación del método SUPG, resulta especialmente útil para la generalización de la técnica a problemas en dos o tres dimensiones. De esta forma, así como en problemas unidimensionales la modificación de las funciones de peso es equivalente a adicionar un término difusivo adicional que actúa en la dirección del flujo, para problemas con una o dos dimensiones adicionales, se debe garantizar que el efecto de la difusión artificial actúe contrarrestando el efecto advectivo, el cual solo opera en la dirección de la velocidad 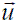. De acuerdo con este planteamiento, una perturbación sobre la función de forma, como la escrita en la ecuación (14), solo logra estabilizar el efecto advectivo en la dirección x. De forma análoga se podría perturbar la función de ponderación para estabilizar la advección en la dirección y, como se muestra en (15).

De esta forma, para lograr estabilizar la solución en la dirección de una velocidad bidimensional, se requiere ponderar las perturbaciones planteadas en (14) y (15), tal como se muestra en (16) [28].

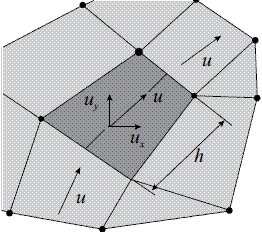
Donde u_x y u_y son las componentes de la velocidad en las direcciones globales x - y, en tanto que es el coeficiente de perturbación calculado de acuerdo con (6), y h es una dimensión característica como la mostrada en la figura 3.

Figura 3 Línea de corriente al interior de un elemento bidimensional

Implementación del método de los elementos finitos con SUPG

Al aplicar el método de los residuos ponderados a la parte estacionaria de la ecuación diferencial de difusión-advección, y después de debilitar el término difusivo, se obtiene la expresión (17).

donde ê_n es el vector normal al borde de flujo o borde de Neumann. Empleando ahora aproximaciones por tramos del tipo 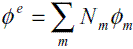, así como la función de peso modificada (16), se llega al sistema de ecuaciones mostrado en (18).

en donde [Φ]^e es el vector de valores nodales del elemento, en tanto que los demás términos se definen de acuerdo con (19), (20), (21) y (22).

En las expresiones (19) a (22), l=m=1,2,3,4 para un elemento cuadrilátero lineal.

Para incorporar la dimensión temporal al problema de la ecuación de difusión-advección planteado previamente, se emplea una discretización temporal como la mostrada en la ecuación (23):

de modo que con θ=1 se llega a un planteamiento totalmente implícito, denominado normalmente esquema Backward-Euler, el cual se define en la expresión (24).

Ahora, aplicando el método de los residuos ponderados a la ecuación (24), de forma similar como se aplicó al término estacionario en (17), se obtiene la expresión (25).

en donde la matriz [M] se define como se muestra en (26):

El método de las líneas características de Galerkin (MLC)

A diferencia del método de Petrov-Galerkin, el cual es planteado como una técnica de estabilización espacial que puede ser implementada en problemas transitorios, el método de las líneas características es aplicable únicamente a problemas con ecuaciones diferenciales de difusión-advección- reacción en donde se presenten términos temporales. Este método parte del hecho que un planteamiento Lagrangiano de la ecuación temporal de difusión-advección puede eliminar el término no autoadjunto, el cual es causante de la asimetría en la matriz de rigidez y por tanto de la inestabilidad en la solución [18].

Partiendo nuevamente de la ecuación diferencial de difusión-advección (27), se observa que empleando una formulación Lagrangiana, como la planteada con el cambio de variable definido en (28), se elimina el término advectivo, resultando la expresión (29). El cambio de variable (28) consiste en emplear una coordenada material x’, en lugar de una coordenada espacial x, lo cual permite que se eliminen los términos relacionados con las derivadas de posición en el tiempo.

Aplicando una discretización temporal a la expresión (29), se obtiene la ecuación (30), en donde δ es la distancia recorrida por una partícula que se mueve con velocidad media u durante un intervalo de tiempo 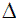t, en tanto que el valor de θ define si el método utiliza una implementación explícita θ = 0, semi-implícita θ = 1/2 o totalmente implícita θ = 1.

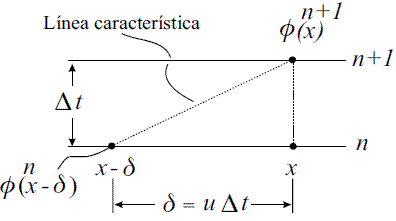
La expresión anterior muestra que lo términos evaluados en el tiempo n se relacionan con la variable x’, mientras que los términos evaluados en el tiempo n+1 se relacionan con la variable x (Figura 4). Es decir, el empleo de la formulación Lagrangiana planteada requiere del uso de técnicas de actualización de malla, lo cual en términos generales no resulta una tarea fácil, ni computacionalmente económica [35].

Figura 4 Movimiento del sistema coordenado y definición de una línea característica

Una forma sencilla de evitar la necesidad de una actualización en la malla, se trata de emplear una aproximación de los términos en tiempo n por medio de una serie de Taylor hacia atrás centrada en x, tal como se muestra en las expresiones (31), (32) y (33).

Incorporando los resultados de estas últimas tres expresiones en la ecuación (30), y teniendo en cuenta que el avance δ puede ser aproximado a través de la ecuación (34) [18], se llega a la ecuación (35), en la cual todos los términos está referidos a la coordenada x.

Aplicando ahora el método Bubnov-Galerkin de residuos ponderados a la ecuación (35), se llega a la expresión debilitada mostrada en (36):

Empleando aproximaciones del tipo 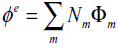, la ecuación de residuos ponderados toma la forma (37):

en donde Φⁿ⁺¹y Φⁿ son los vectores de valores nodales en el tiempo n+1 y n, respectivamente. Los demás términos involucrados en (37) se definen en las ecuaciones (38) a (44).

Expandiendo está técnica al caso bidimensional, y para un planteamiento semi-implícito Crank- Nicolson (θ = 1/2), se llega a la expresión (45).

en donde:

Resultados y discusión

Experimentación numérica

Con el fin de evaluar la precisión y eficiencia de los dos métodos presentados (SUPG-MLC), se analizó el siguiente problema dominantemente advectivo, cuya solución numérica se implementó en lenguaje FORTRAN para diferentes mallas, tal como se muestra a continuación.

Este ejemplo, desarrollado entre otros autores por Wang [36], esta definido por la ecuación diferencial (50), para un dominio Ω = (-0,5,0,5)x(-0,5,0,5).

con k=0,0001 y un campo de velocidad rotacional 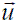= [- 4y,4x] r . Las condiciones de borde definidas para las cuatro fronteras del problema, son condiciones de Dirichlet homogéneas, en tanto que las condiciones iniciales están definidas por la expresión (51), con σ = 0,0477. La solución analítica del problema se plantea en la expresión (52).

en esta última expresión:

Este problema se caracteriza por tener dentro del dominio espacial tanto zonas de convección dominante, ubicadas cerca de los bordes del problema, como zonas de difusión dominante, ubicadas en la región cercana al centro del dominio. Estas zonas están definidas espacialmente y no cambian en el tiempo, dado que el coeficiente de difusión y el campo de velocidades no son función de esta variable. Por lo anterior, este caso resulta especialmente interesante para evaluar la capacidad de las técnicas numéricas para aproximar problemas con condiciones advectivas variables sobre todo el dominio.

Los resultados obtenidos en este ejemplo se muestran en las figuras 5, 6, 7 y 8, considerando tanto la formulación con MLC, como con el método SUPG. En ambos planteamientos se empleó una discretización temporal con pasos de tiempo 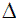t=0,0005 y un tiempo final t_f =0,5.

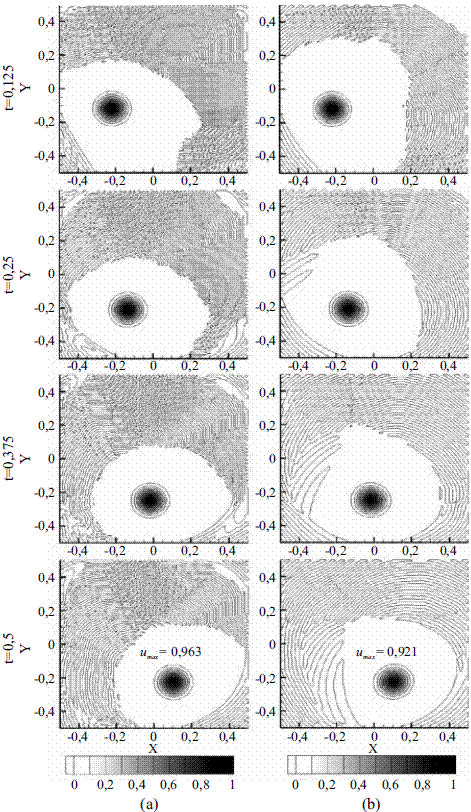
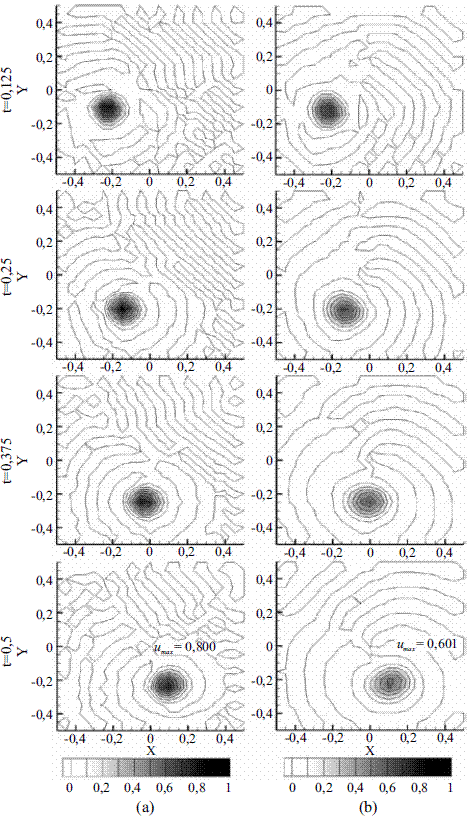
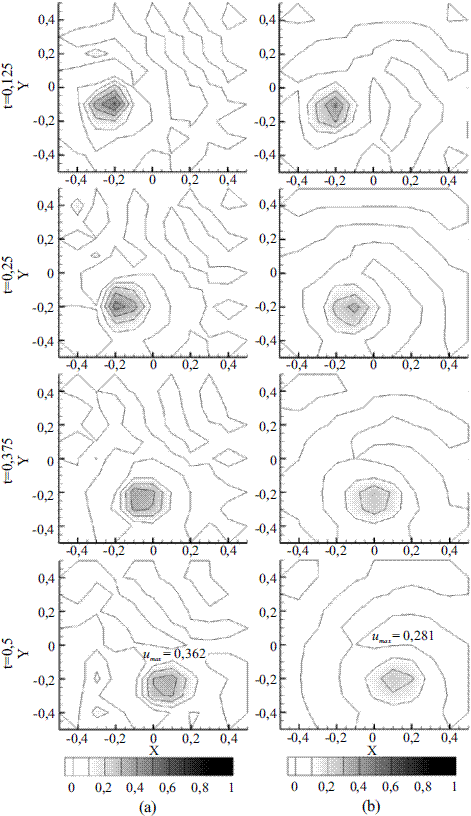
Para la primera malla, formada por 10.000 elementos (h=0,01, figura 5), se obtiene un número máximo de Peclet igual a 141, ubicado en los vértices del dominio, el cual decrece a medida que se está más cerca del centro del cuadrado, alcanzando un valor mínimo de cero en este punto. Se observa, en la figura 5, que las soluciones obtenidas por los dos métodos (MLC y SPUG) son similares en cuanto a magnitud y desplazamiento de la función gaussiana. Sin embargo, se presentan en la solución por líneas características, pequeñas inestabilidades que se evidencian en la irregularidad de las líneas de contorno. Dichas inestabilidades en la solución con MLC crecen conforme se aumenta el tamaño de los elementos y correspondientemente el número de Peclet, tal como se observa en la figura 6 (malla con 400 elementos, h=0,05), y especialmente en la figura 7 (malla con 100 elementos, h=0,1), en donde debido a los altos valores de P_e (máximo cercano a 1.400) las oscilaciones alcanzan valores comparables con la altura de la función gaussiana. Otro aspecto importante es la componente de difusión numérica que exhiben las dos soluciones (mayormente la alcanzada con SUPG), la cual se incrementa a medida que se aumenta el tamaño de los elementos en la malla.

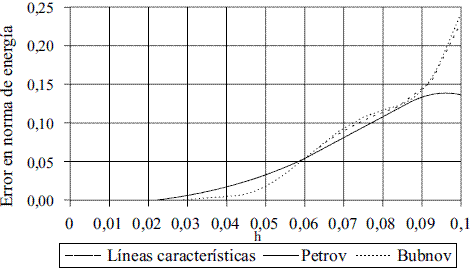
Por otro lado, la figura 8 muestra gráficas de convergencia del error en norma L² para tres planteamientos de elementos finitos: el método de líneas características, el método SUPG y el método convencional o Bubnov-Galerkin. Este error es calculado como la integral, sobre el tiempo y el espacio, del cuadrado de la diferencia entre la solución analítica y la aproximación lograda [37]. En las curvas de la figura 8 se observa como la gráfica de convergencia obtenida para MLC es muy similar a la gráfica del método convencional, cuya velocidad y forma de convergencia se diferencia claramente del comportamiento mostrado por la curva obtenida con SUPG.

Figura 5 Soluciones transitorias obtenidas para el caso de estudio 1 empleando h=0,01 y el MLC (a) y el método de SUPG (b)

Figura 6 Soluciones transitorias obtenidas para el caso de estudio 1 empleando h=0,05 y el MLC (a) y el método de SUPG (b)

Conclusiones

Se analizó un problema de difusión-advección empleando dos técnicas de solución numérica: el método de Petrov-Galerkin en contracorriente (SUPG) y el método de las líneas características de Galerkin (MLC). Para el caso analizado, las aproximaciones alcanzadas con el método SUPG muestran que aún para números de Peclet tan altos como 1.400, se logran soluciones libres de oscilaciones falsas. Por el contrario el MLC no muestra una buena capacidad de estabilizar la solución cuando los números de Peclet se elevan considerablemente, en este caso particular las oscilaciones comenzaron a ser notorias para mallas con tamaño promedio superior a h=0,05 y P_e=700. Por otro lado, se pudo establecer que el método SUPG exhibe una difusión numérica más elevada que la presentada por las soluciones con el método de las líneas características, aunque en ambos casos esta difusión creció rápidamente con el aumento en el tamaño de la malla. La gráfica de convergencia trazada (error en norma de energía vs. tamaño de elemento) muestra que para bajos números de Peclet (lo que equivale a mallas finas) el MLC es más exacto que el método SUPG, no obstante cuando la malla se hace más grande (lo que equivale a número de Peclet altos), el MLC no es capaz de corregir las inestabilidades, las cuales hacen crecer el error por encima del valor alcanzado con el método SUPG.

Figura 7 Soluciones transitorias obtenidas para el caso de estudio 1 empleando h = 0,1 y el MLC (a) y el método de SPUG (b)

No obstante la mayor exactitud del método MLC sobre el SUPG en los casos con bajos números de Peclet, se encontró que el comportamiento del MLC difiere muy poco de la técnica convencional o método de Bubnov-Galerkin, lo cual sumado a la mayor dificultad en la implementación computacional del mismo, hace que este sea poco competitiva frente al SUPG.

Figura 8 Gráfica de convergencia del error en norma de energía para las soluciones alcanzadas en el caso 1

Referencias

1. D. Garzón, C. Galeano, C. Duque. “Aplicación del método Petrov-galerkin como técnica de estabilización de la solución en problemas unidimensionales de convección-difusión -reacción”. Rev. Fac. Ing. Univ. Antioquia. Vol. 47. 2009. pp. 73-90.        [ Links ]

2. I. Babuska, F. Ihlenburg, E. Paik, S. Sauter. “A generalized finite element method for solving the Helmholtz equation in two dimensions with minimal pollution”. Computer Methods in Applied Mechanics and Enginnering. Vol. 128. 1995. pp. 325-359.        [ Links ]

3. D. Garzón Alvarado, J. García Aznar, M. Doblare. “Appearance and location of secondary ossification centres may be explained by a reaction-diffusion mechanism”. Computers in biology and medicine. Vol. 39. 2009. pp. 554-561.        [ Links ]

4. S. Ferreira, M. Martins, M. Vilela. “Reaction-diffusion model for the growth of avascular tumor”. Physical Review. Vol. 65. 2002. pp. 21-907.        [ Links ]

5. M. Chaplain, A. Ganesh, I. Graham. “Spatio-temporal pattern formation on spherical surfaces: Numerical simulation and application to solid tumor growth”. J. Math. Biol. Vol. 42. 2001. pp. 387-423.        [ Links ]

6. A. Madzvamuse. “A Numerical Approach to the Study of Spatial Pattern Formation in the Ligaments of Arcoid Bivalves”. Bulletin of Mathematical Biology, Vol 64. 2002. pp. 501-530.        [ Links ]

7. S. Kondo, R. Asai. “A reaction-diffusion wave on the skin of the marine anglefish, Pomacanthus”. Nature. Vol. 376. 1995. pp. 765-768.        [ Links ]

8. F. Crauste, M. Lhassan, A. Kacha. “A delay reactiondiffusion model of the dynamics of botulinum in fish”. Mathematical Biosciences. Vol. 216. 2008. pp. 17-29.        [ Links ]

9. F. Rossi, S. Ristori, M. Rustici, N. Marchettini, E. Tiezzi. “Dynamics of pattern formation in biomimetic systems”. Journal of Theoretical Biology. Vol. 255. 2008. pp. 404-412.        [ Links ]

10. B. Rothschild, J. Ault. “Population-dynamic instability as a cause of patch structure”. Ecological Modelling. Vol. 93. 1996. pp. 237-239.        [ Links ]

11. T. Nozakura, S. Ikeuchi. “Formation of dissipative structures in galaxies”. Astrophys. J. Vol. 279. 1984. pp. 40-52.        [ Links ]

12. C. Costa, M. Vilhena, D. Moreira, T. Tirabassi. “Semianalytical solution of the steady three-dimensional advection-diffusion equation in the planetary boundary layer”. Atmospheric Environment. Vol. 40. 2006. pp. 5659-5669.        [ Links ]

13. R. Smith. “Optimal and near-optimal advectiondiffusion finite-difference schemes iii. Black-Scholes equation”. Proceedings: Mathematical, Physical and Engineering Sciences. Vol. 456. 2000. pp. 1019-1028.        [ Links ]

14. O. Richter. “Modelling dispersal of populations and genetic information by finite element methods”. Environmental Modelling & Software. Vol. 23. 2008. pp. 206-214.        [ Links ]

15. L. Ferragut, M. Asensio, S. Monedero. “A numerical method for solving convection-reaction-diffusion multivalued equations in fire spread modelling”. Advances in Engineering Software. Vol. 38. 2007. pp. 366-371.        [ Links ]

16. A. Rubio, A. Zalts, C. El Hasi. “Numerical solution of the advection-reaction-diffusion equation at different scales”. Environmental Modelling & Software. Vol. 23. 2008. pp. 90-95.        [ Links ]

17. W. Hundsdorfer, J. Verwer. Numerical Solution of timedependent Advection-Diffusion-Reaction Equations. Ed. Springer. Berlin. 2007. pp 10-20.        [ Links ]

18. O. Zienkiewicz, R. Taylor. “Convection dominated problems -Finite element approximations to convection-diffusion equation”. Finite Element Method. Ed. Butterworth-Heinemann College. Barcelona. Vol. 3. 2000. pp. 13-90.        [ Links ]

19. O. Zienkiewicz, R. Taylor. “Generalization of finite element concepts. Galerkin weighted residual and variational approaches”. Finite Element Method. Ed. Butterworth-Heinemann College. Barcelona. Vol. 1. 2000. pp. 39-86.        [ Links ]

20. F. Brezzi, D. Marini, A. Russo. “Applications of the pseudo residual-free bubbles to the stabilization of convection-diffusion problems”. Computer Methods in Applied Mechanics and Engineering. Vol. 166. 1998. pp. 51-63.        [ Links ]

21. O. Zienkiewicz, R. Löhner, K. Morgan, S. Nakazawa. “Finite Elements in Fluid mechanics- a decade of progrgess”. Finite Elements in Fluids. Vol. 5. 1984. pp. 1-26.        [ Links ]

22. E. Oñate. “Derivation of stabilized equations for numerical solution of advective diffusive transport and fluid flow problems”. Computer Methods in Applied Mechanics and Enginnering. Vol. 151. 1998. pp. 233- 265.        [ Links ]

23. J. Chrispell, V. Ervin, E. Jenkins. “A fractional step ?-method for convection-diffusion problems”. Journal of Mathematical Analysis and Applications. Vol. 333. 2007. pp. 204-218.        [ Links ]

24. T. Hughes, L. Franca, G. Hulbert, Z. Johan, F. Sakhib. “The Galerkin least square method for advective diffusion equations”. Recent Developments in Computational Fluid Mechanics. AMD 94-ASME. 1988. pp. 1-20.        [ Links ]

25. O. Zienkiewicz, R. Gallagher, P. Hood. “Newtonian and non-Newtonian viscous impompressible flow. Temperature inducedflows and finite elements solutions”. The Mathematics of Finite Elements and Applications. Ed. Academic Press. London. 1975. pp. 1-650.        [ Links ]

26. I. Christie, D. Griffiths, O. Zienkiewicz. “Finite element methods for second order differential equations with significant first derivatives”. International Journal for Numerical Methods in Engineering. Vol. 10. 1976. pp. 1389-1396.        [ Links ]

27. O. Zienkiewicz, J. Heinrich, P. Huyakorn, A. Mitchel. “An upwind finite element scheme for two dimensional convective transport equations”. International Journal for Numerical Methods in Engineering. Vol. 11. 1977. pp. 131-144.        [ Links ]

28. T. Hughes, A. Brooks. “A multidimensional upwind scheme with no crosswind diffusion”. Finite Element Method for Convection Dominated Flows (ASME). Vol. 34. 1979. pp. 19-35.        [ Links ]

29. T. Hughes, L. Franca, G. Hulbert. “A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective diffusive equations”. Computer Methods in Applied Mechanics and Enginnering. Vol. 73. 1989. pp. 173- 189.        [ Links ]

30. C. Baiocchi, F. Brezzi, L. Franca. “Virtual bubbles and Galerkin/least-square type methods”. Computer Methods in Applied Mechanics and Enginnering. Vol. 105. 1993. pp. 125-141.        [ Links ]

31. I. Harari, T. Hughes. “Stabilized finite element methods for steady advection-diffusion with production”. Computer Methods in Applied Mechanics and Enginnering. Vol. 115. 1994. pp. 165-191.        [ Links ]

32. A. Russo. “Bubble stabilization of the finite element method for the linearized incompressible Navier- Stokes equation”. Computer Methods in Applied Mechanics and Enginnering. Vol. 132. 1996. pp. 335- 343.        [ Links ]

33. B. Cockburn, G. Karniadakis, C. Shu. Discontinuous Galerkin Methods, Theory, Computational and Application. Ed. Springer. Berlin. 2000. pp.1-470.        [ Links ]

34. R. Araya, E. Behrens, R. Rodríguez. “An adaptive stabilized finite element scheme for the advection- reaction-diffusion equation”. Applied Numerical Mathematics. Vol. 54. 2005. pp. 491-503.        [ Links ]

35. W. Shyy, H. Udaykumar, M. Rao, R. Smith. “Numerical techniques for fluid flows with moving boundaries”. Computational Fluid Dynamics with Moving Boundaries. Ed. Dover Publications. Philadelphia. 2007. pp. 1-19.        [ Links ]

36. H. Wang, H. Dahle, R. Ewing, M. Espedal, R. Sharpley, S. Man. “An ELLAM scheme for advection-diffusion equations in two dimensions”. SIAM J. Sci. Comput. Vol. 20. 1979. pp. 2160-2194.        [ Links ]

37. E. Kreyszig. “Inner product spaces. Hilbert Spaces”. Introductory Functional Analysis with Applications. Ed. wiley. New York. 1989. pp. 127-208.        [ Links ]

(Recibido el 7 de abril de 2009. Aceptado el 23 de septiembre de 2009)

^*Autor de correspondencia: teléfono: + 57 +1 + 316 50 00, correo electrónico: dagarzona@unal.edu.co (D. Garzón)