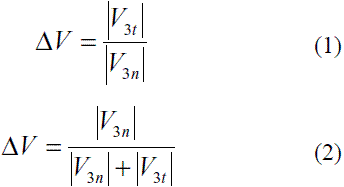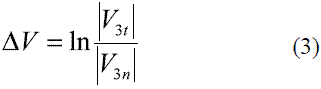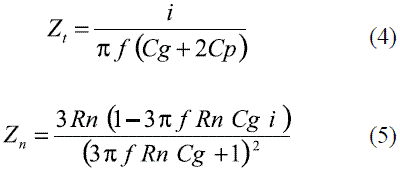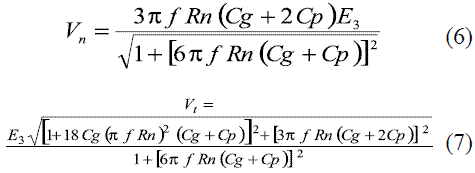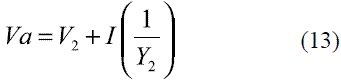Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230versão On-line ISSN 2422-2844
Rev.fac.ing.univ. Antioquia n.52 Medellín abr./jun. 2010
Improvement of the third harmonic based stator ground fault protection for high resistance grounded synchronous generators
Mejoramiento de la protección basada en el tercer armónico contra fallas a tierra del estator de generadores síncronos aterrizados mediante alta impedancia
Byron Ruíz-Mondragón*, Juan Mora-Flórez , Sandra Pérez-Londoño
Grupo de Investigación en Calidad de Energía Eléctrica y Estabilidad (ICE3) Pereira, La Julita, Universidad Tecnológica de Pereira, Programa de Ingeniería Eléctrica, Pereira, Colombia
Abstract
This paper shows a comparison and a proposed improvement of three different approaches based on the measurements of the third harmonic of voltage which are aimed to obtain a 100% protection of the stator winding in the case of ground faults in high resistance grounded synchronous generators. These three different methods are based in voltage measurements at the neutral and terminal connections, and also in the ratio of these measurements. From the results obtained in a real synchronous generator there are advantages of the scheme based on the ratio of the voltages measured at terminals and neutral, in the case of using the voltage threshold strategy. However, by using the proposed alarm-trip logic, remarkable improvements could be obtained in the case of detecting high impedance ground faults. Finally, this work may help to develop useful protective devices which detect ground faults at the synchronous generator stator windings. Although a first fault normally does not cause any problem, this have to be removed before the occurrence of a second ground fault which could cause severe machine damages and the consequent outage.
Keywords: 100 % stator ground fault protection, synchronous generator, third harmonic, phase-ground fault
Resumen
En éste artículo se presenta una comparación y una propuesta de mejoramiento de tres diferentes métodos de protección del 100% del estator en el caso de fallas a tierra, aplicados a generadores síncronos aterrizados mediante una alta resistencia. Los tres métodos están basados en las mediciones de tercer armónico de tensión en el neutro, en los terminales de la máquina y en la relación de las dos medidas anteriores. De los resultados obtenidos en generador síncrono real, se puede apreciar que el esquema basado en la relación de las tensiones de tercer armónico medido en los terminales y en el neutro es la mejor alternativa, en el caso de utilizar la estrategia de umbrales de tensión. Sin embargo, mediante la utilización de una estrategia propuesta basada en una lógica para alarma y disparo, se pueden apreciar notables mejoras en la capacidad de detección de fallas a tierra de alta impedancia. Finalmente, este trabajo puede contribuir al desarrollo de elementos de protección útiles para detectar fallas a tierra en los devanados del estator de un generador síncrono. Aunque una primera falla normalmente no causa ningún problema, ésta tiene que ser atendida prontamente antes que una segunda falla pueda causar graves daños en la máquina y su consiguiente salida del servicio.
Palabras clave: Protección del 100% del estator ante falla a tierra, generador síncrono, tercer armónico, falla fase tierra
Introduction
Ground faults at the synchronous machine stator are common and these cause current flows through the neutral conductor. The current magnitude depends of the grounding type (high, medium and low impedance). The high impedance method is frequently used because in the case of faults the current magnitude is relatively low [1, 2]. The most commonly used protective scheme in the case of high impedance grounding consists on an overvoltage relay (59), used to protect the 90% or 95% of the stator winding. The 5% or 10% of the remaining stator part is not protected in the case of ground faults, because the voltage generated in the faulted winding decreases as close is the fault point from the neutral connection and it is not enough to drive the protection (In fact, a fault at the neutral node would produce voltage and current of zero magnitude) [3].
A stator ground fault close to the neutral point is not immediately catastrophic because: 1) it will not drive high current due to the small magnitude of the short circuited voltage and 2) the grounding impedance restricts the fault current. However an undetected stator ground fault near the neutral could develop into a phase to phase fault or turn to turn fault. Moreover, if a stator ground fault close to the neutral point remains undetected, it bypass the grounding resistor and the conventional protection, and then a second ground fault toward the terminal could lead to catastrophic consequences. Therefore, 100% stator ground fault is needed for large synchronous machines, where the most commonly used methods consider a subharmonic injection and the measurement of the third harmonic [4, 5, 6].
This paper focuses on the application of the third harmonic principle and is devoted to present a comparative analysis and an improvement of three different approaches. First, the basic aspects of the analyzed methods are presented. Next, the theoretical evaluation of the faulted and nonfaulted systems is given as a fundamental part of the proposed improvements for the 100% stator ground fault protection methods. Then, the main results and a comparative analysis are presented, and finally the main conclusions are presented.
Methodology
Method of third harmonic
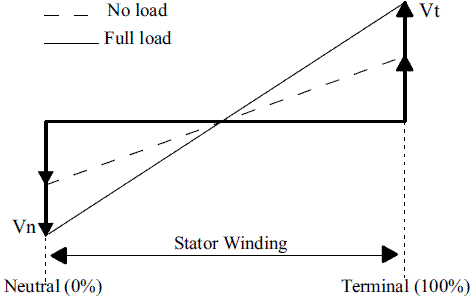
This method uses a comparison of the third order component of the voltage measured at the synchronous generator terminal (Vt) or at the neutral (Vn) connections. This harmonic magnitude varies according to the load level, the measurement point and the fault location along the winding. Its normal values are between 1 and 6 % of the nominal generator voltage, in the case of non faulted windings [7]. Figure 1 shows the third harmonic voltage distribution generated along the stator windings during normal operating conditions, considering variations in the machine load [4, 5].
Figure 1 Magnitude of the third harmonic at the stator winding considering non fault situations
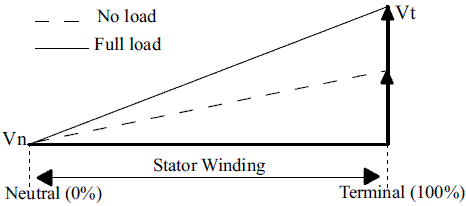
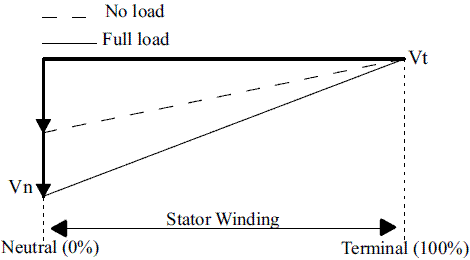
Considering a ground fault at the neutral connection, the third harmonic at this node decreases to zero. However, the value of the third harmonic at terminal is different from zero as it is shown in figure 2. Finally and considering a ground fault at the generator terminals, the effect is the opposite of the previously described. The magnitude of the third harmonic voltage at the neutral connection becomes maximum while in terminals it decreases to zero, as it is presented in figure 3 [4, 8].
Considering the third harmonic magnitude variations between neutral and terminal nodes of the synchronous generator, three types of 100 % stator protection schemes are proposed: the first one is considering the undervoltage of the third harmonic; the second is considering the overvoltage of the third harmonic; and the third scheme is based on the comparison of the two previous schemes [9, 10, 11].
Figure 2 Magnitude of the third harmonic at the stator winding considering a ground fault in the neutral
Figure 3 Magnitude of the third harmonic at the stator winding considering a ground fault in terminals
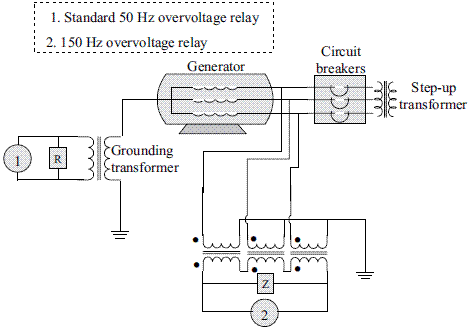
Undervoltage of the third harmonic component (Scheme 1)
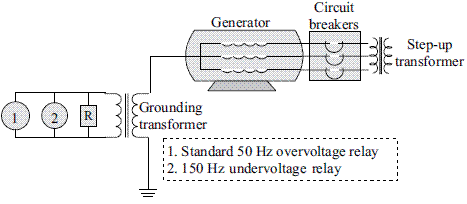
This scheme is based on the measurement of the third harmonic component of voltage at the neutral connection of the synchronous generator, as presented in figure 4. In this method, the third harmonic voltage is measured at the neutral. There is a 150 Hz relay tuned to detect third harmonic voltage and a standard 50Hz relay tuned to the fundamental frequency.
Overvoltage of the third harmonic component (Scheme 2)
This scheme is based on the measurement of the third harmonic of voltage at the terminal connection of the generator, see figure 5.
The two previous schemes normally use a relay 27H able to determine frequencies from 150 to 180 Hz. This relay detects variations at the magnitude of the third harmonic causing alarm or trip.
Figure 4 Protective scheme used to detect under voltage of the third harmonic
Figure 5 Protective scheme using over voltage of the third harmonic
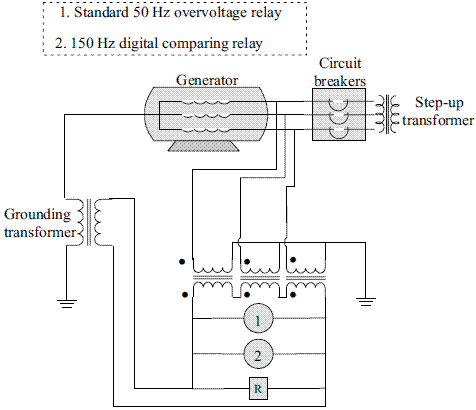
Ratio of the third harmonic components (Scheme 3)
This method is based on the comparison of third harmonic voltages using several mathematic relations which should make the protective device more susceptible to the variation of these voltages. In this paper, three different relations as the presented from (1) to (3) are analyzed.
In the above equations, V3n corresponds to the third harmonic voltage at the generator neutral and V3t is the third harmonic voltage at the generator terminals. In figure 6 the ratio scheme is presented [7, 11, 12].
Figure 6 Protective scheme of third harmonic voltage using the ratio method
Theoretical evaluation of the non-faulted and faulted models
The three previously described protective schemes are here analyzed according to two models, previously developed to represent the stator winding equivalent circuit [7]. The first model is the equivalent scheme of the system under normal condition operation while the second one is equivalent to the system working under fault conditions.
Theoretical analysis for the non fault model
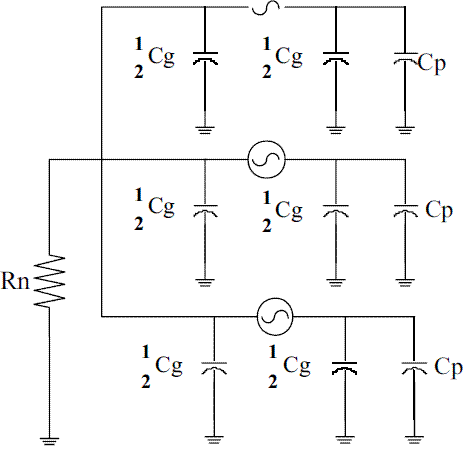
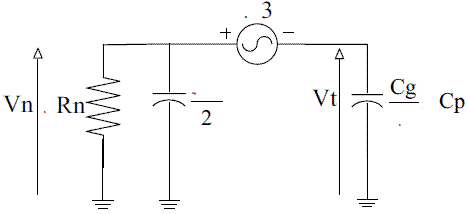
The equivalent circuit developed for non fault conditions is presented in figure 7. As is mentioned before, the third harmonic voltage appears as zero-sequence quantities. Then the third harmonic voltage produced by the synchronous generator is distributed between the terminal and the neutral shunt impedances governing the zero-sequence. In figure 8 it is possible to see this zero-sequence circuit obtained from figure 7, where Rn is the grounding resistor, Cg is the phase capacitance to ground of the generator stator winding, Cp is the total external phase capacitance of the system as seen from the generator, and E3 is the generated third harmonic voltage. Finally, figure 9 is obtained as a simplification of figure 8.
Figure 7 Equivalent synchronous generator model considering non fault conditions
Following, from figure 9 and using the proposed equations presented in (4) and (5) it is possible to obtain the impedances at the terminal and neutral nodes, respectively.
Where i indicates the imaginary operator and f is the power frequency.
Figure 8 Zero-sequence circuit
Figure 9 Simplified zero-sequence circuit
Solving circuit proposed in figure 9, equations (6) and (7) are then obtained for the voltage at the neutral and terminals, respectively.
Theoretical analysis of the faulted model
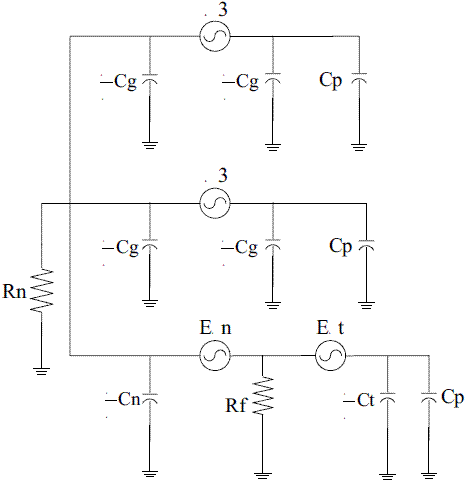
The equivalent circuit developed to consider under faulted conditions is presented in figure 10. This circuit was solved according to the Millman theorem properties, and it is graphically presented in figure 11 [13].
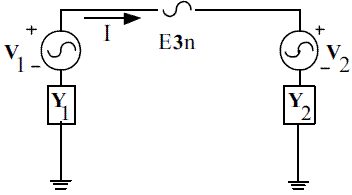
From figure 11, V1 and V2 are the equivalent voltages as seen from the left and the right sides of E3n at the faulted winding. Similarly, the admittances Y1 and Y2 have the same meaning. Additionally, E3n corresponds to kE3 and E3t is associated to (1-k)E3, where both are the third harmonic voltages produced by the stator winding between the generator neutral and the ground-fault location k, and between the generator terminal and the ground fault location k, respectively. k is given as a per unit value of the stator length and it is measured from the neutral to the ground fault location. Cg is the phase capacitance of the generator stator winding to ground; Cp is the total external phase capacitance of the system as seen from the generator.
Figure 10 Equivalent synchronous generator model considering fault conditions
Figure 11 Simplified circuit using Millman theorem
Finally, Cn corresponds to Cg, while Ct is equivalent to (1-k)Cg. Both are the phase capacitances to ground of the generator stator winding between the ground-fault location k and the generator neutral, and between the generator terminal and the ground-fault location k, respectively. Rn is the ground resistor.
As described before, equations from (8) to (11) are obtained by applying the Millman theorem to the system presented in figure 10.
The flowing current (I) is then obtained as it is presented in (12).
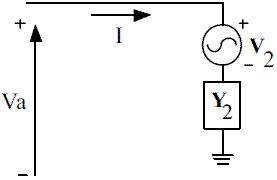
Figure 12 shows an equivalent circuit obtained from figure 11, where Va is the equivalent voltage obtained at the right side of the source E3n.
Voltage Va is obtained as it is presented in (13).
From the proposed equivalent, voltages at the neutral (Vn) and terminal (Vt) under fault conditions are obtained as it is presented in (14) and (15).
Figure 12 Equivalent circuit used to find Vt and Vn
Alarm-trip logic proposed for the 100% ground fault protection
The detectable values of the fault resistance, in the case of all of the proposed 100% ground fault protection alternatives which use the third harmonic method, were obtained by considering the criteria presented in this section. This corresponds to a proposed improvement of the classical voltage threshold alternatives.
In the case of all of the schemes proposed for the 100% ground protection, the ranges were no alarm or trip signal should be presented are obtained. All of the possible variations of the third harmonic voltage due to changes on the connected load and errors in the meters are considered for this analysis.
The logic used to determine the presence of trip or alarm for both, under and overvoltage of the third harmonic component (schemes 1 and 2, respectively), is presented in figure 13, and it is based on the comparison of the values of the third harmonic of the voltage measured (denoted with the additional subindex m) and those normal values as the present in figure 14.
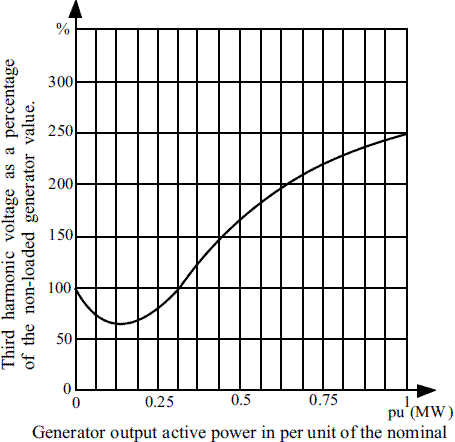
The behavior of the third harmonic voltage is described by curves as shown in figure 14 [7, 10]. These variations are particular for each one of the generator machines and are due small imperfections in the winding distribution during the fabrication process, which cause small voltage unbalances [9].
Finally, the alarm-trip logic used in the case of scheme 3 is based on the definition of the maximum non trip voltages at the neutral and the terminals defined by the schemes 1 and 2, and by using one of the equations presented form (1) to (3).
Figure 13 Alarm-trip logic used for the undervoltage (scheme 1) or overvoltage (scheme 2) of the third harmonic component
Figure 14 Third harmonic voltage typical variations caused by changes in the output active power
Results
This section is aimed to present the tests of the different alternatives of the 100% stator winding protective methods. The proposed protection is designed to cover the first 10% of the stator windings, estimated from the neutral to terminals.
Test system
To obtain the proposed comparison, a real generator machine is used in tests and these parameters are the presented in table 1. In addition and considering the influence of the load, the third harmonic voltages at the machine used in tests experience changes from the 1% to the 6% of the machine nominal voltage.
Table 1 Typical values for a unit-connected generator
Validation of the proposed third harmonic generator models
The synchronous generator models proposed in figures 7 and 10 for steady state and fault conditions respectively were simulated using Matlab-Simulink®. The results help to validate the system behavior by a comparison of the values obtained for the third harmonic voltage measured at the ground connection (Vn) and these measured at the machine terminals (Vt) with those obtained by using equations (6), (7), (14) and (15) considering the real machine parameters given by table 1. Errors in the estimation are lower than 3% were obtained.
Fault resistance estimation using the voltage thresholds
The first strategy is based on the determination of the normal values of the third harmonic of voltage at the terminals and the neutral of the synchronous generator. Considering that the third harmonic voltages are strongly related to the generator load as it is graphically presented in figure 14, it is important to determine how this dependence affects the detectable values of the fault resistance in all of the analyzed protection schemes.
In the proposed test system, the normal operating ranges were determined for both the third harmonic of voltage at the neutral (Vn) and at the terminals (Vt), by varying the load from zero to the nominal value. The normal operating intervals for the third harmonic voltage measured at the neutral is [39.1 - 234.5 volts], while in the case of the terminal voltage is [31.2 - 186.6 volts].
Using the classical thresholds strategy to determine the maximum fault resistance to be detected in the case of the undervoltage scheme, different fault situations were analyzed using the circuit presented in figure 10. In all of the situations, the voltage at the neutral (Vn) was measured and these values which are lower than minimum voltage normal operating conditions correspond to faults which could be detected in the case of scheme 1. A similar strategy is used to determine those faults that could be detected using the overvoltage scheme, but considering values of terminal voltage (Vt) which are higher than the maximum voltage during normal operating conditions. In the case of the ratio scheme, the values of the third harmonic measured during faults are compared with those obtained in the case of non fault situations, and as a consequence the dependence on the load is greatly reduced considering the division of the voltages at the neutral and the terminals as proposed from equation (1) to (3).
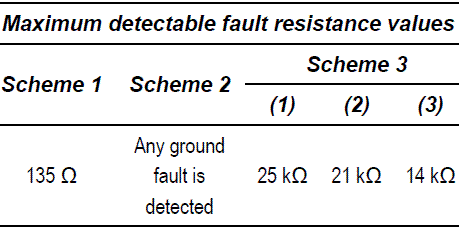
According to preliminary test performed in the proposed real synchronous generator, the obtained values for the maximum fault resistances which are detectable by using each one of the three proposed schemes are presented in table 2. According to this table, the undervoltage of the third harmonic (scheme 1) is capable to detect fault resistances lower than 135 Ω, causing the inoperability of this alternative to detect medium and high resistant faults. In the case of the overvoltage of the third harmonic (scheme 2), there is not possible to detect any ground fault because the overlapping of the normal operation range values of the third harmonic and those values measured in case of faults. Finally, the alternative which uses the ratio of the third harmonic components (scheme 3) as it is presented from equation (1) to (3), due its high sensibility to the voltage variations could detect high resistance faults.
Table 2 Maximum fault resistance values detectable by the analyzed protective methods using the voltage thresholds (Undervoltage, overvoltage and ratio of the third harmonic of voltage)
Fault resistance estimation using the alarmtrip logic
As proposed improvement of the protection method, the alarm-trip logic previously explained is considered to determine the maximum values of fault resistance which could be detected in the case of ground faults. These values are estimated by assuming a generator operational situation given by an equivalent load which causes the percentage of the third harmonic from 1 to 6% on the nominal voltage, as it is presented on horizontal axis of figure 15.
Figure 15 Maximum fault resistance values detectable by the protective methods using the alarmtrip logic (Undervoltage, overvoltage and ratio of the third harmonic of voltage)
For each load condition, a tolerance value of 5% is applied to determine if the generator would be or not under fault condition. These results are presented in the case of the three 100% protection schemes and using measurements of the third harmonic of voltage from the test system.
In the case of the scheme 3 (ratio of the third harmonic), the relation presented in equations (1), (2) and (3) were tested, as it is present in figure 15 as scheme 3(1), scheme 3(2) and Scheme 3(3), respectively.
Finally, the different schemes were tested in the case of nine values of third harmonic voltage (nine different load conditions) to cover all variation range. The obtained results shows small variations in the maximum fault resistance detected, showing the reduced dependence of the proposed protection strategy and the synchronous generator load condition.
Analysis
Considering the first protection strategy which uses the voltage thresholds (Table 2), all of the variations in the magnitude of the third harmonic voltages caused by load changes from zero to nominal load, the maximum fault resistance detected using the Scheme 1 (undervoltage) is nearly 135 Ω. Considering the Scheme 2 (overvoltage) it is not possible to use this method to detect faults for any load condition, while using the Scheme 3 (comparison) the maximum fault resistance detected is 25 kΩ.
As a proposed improvement using the alarm-trip logic presented, it is notice how the capability to detect high impedance faults using the analyzed methods is increased (Figure 15). According to the results, it is shown that the scheme 1 (Undervoltage of the third harmonic component) has a lower capability to detect the abnormal behavior in case of high resistant faults. Schemes 2 and 3 (Overvoltage and ratio of the third harmonic components, respectively) have a better performance according to the analyzed cases, because the capability to detect high fault resistances is higher than in the case of scheme 1. This characteristic is desirable because it is useful to detect possible problems in the insulation level of the synchronous generator.
Finally, the alarm-trip logic proposed helps to deal with the variation in the magnitude of the third harmonic of voltage caused by load changes as it is presented in figures 2, 3 and 14. This seems to be an adequate and straightforward strategy to overcome the main disadvantage of the three methods for protecting 100% stator winding in presence of ground faults, which is related to the variation of the third harmonic voltages.
Conclusions
All of the alternatives of the third harmonic of voltage previously analyzed and tested show an interesting way to develop a 100% protective scheme for the synchronous generator stator winding in the case of ground faults.
In such cases where the curve which relates the normal value of the third harmonic voltages and the generator load is not available, the voltage threshold based strategy helps to implement a very constrained application using the undervoltage scheme. The use of the overvoltage strategy in not useful due the restrictions associated to the overlapping of several values of the third harmonic voltages in normal operating conditions with such values in case of stator ground faults. Finally, the use of the ratio scheme shows an interesting behavior making possible the detection of high impedance faults.
The use of the proposed alarm-trip logic is an interesting alternative which helps to improve the protection performance, making possible the detection of high impedance faults in all of the three third harmonic based schemes. However, the ratio based scheme helps to obtain the best performance in high impedance fault determination.
Despite to the previously explained, the under voltage scheme is the cheapest alternative to the 100% protection of the synchronous generator, due the reduced requirements in associated equipment as potential transformers and complex relays.
Finally, the analyzed strategies were adjusted for protecting the last 10% of the stator winding in the case of ground faults. Such devices have to be installed together to the classical ground fault protection for covering all of the stator winding.
References
1. IEEE Standards Board. IEEE Guide for AC generator protection. Power System Relaying Committee of the IEEE Power Engineering Society. 1995. pp. 1-120. [ Links ]
2. IEEE C62-92. Guide for the Application of Neutral Grounding in Electrical Utility Systems Part Il- Grounding of Synchronous Generator Systems. Power System Relaying Committee. 1989. pp. 7-18. [ Links ]
3. J. Blackburn. Protective relaying - principles and application. 2nd. ed. Ed. Marcell Dekker. New York. 1994. pp. 215-316 [ Links ]
4. D. Reimert. Protective Relaying for Power Generation Systems. Ed. CRC Press Taylor and Francis Group. Boca Raton, Florida, USA. 2006. pp. 132-155. [ Links ]
5. J. Mora Flórez, G. Olguín, L. Giraldo. Evaluación de la protección del estator de un generador ante fallas a tierra usando el método de inyección subarmónica. Rev. Ingeniería y Competitividad. Vol.10. 2008. pp. 21-30. [ Links ]
6. L. Giraldo, J. Mora Flórez, G. Olguín. Análisis sensitividad del método de inyección subarmónica para la protección del 100% del estator del generador síncrono ante fallos fase tierra. Revista Tecnura - U. Distrital. Vol. 20. 2007. pp. 52-60. [ Links ]
7. R. Alcántara, F. García. 100% Stator ground fault protection a comparison of two protection methods. Department of Industrial Electrical Engineering and Automation. Lund Institute of Technology. MSc. Thesis. 2005. pp. 20-46. [ Links ]
8. J. Pope. A comparison of 100% stator ground fault protection schemes for generator stator windings. IEEE Trans on Power Apparatus and Systems. Vol. 103. 1984. pp. 832-840. [ Links ]
9. M. Fulczyk. Zero-sequence voltages in unit-connected generator for different methods of grounding generator neutral. ABB Corporate Research. Krakow. Poland Developments in Power System Protection. Conference Publication No.479 0 IEE. 2001. pp. 499-502. [ Links ]
10. T Nenglin, Y. XiangGen, C. DeShu. Analysis of stator ground protection schemes for hydro-generator of three gorges power plant based on zero sequence voltages. IEEE Power Engineering Society Winter Meeting. Singapore. Vol. 3. 2000. pp. 1888-1893. [ Links ]
11. W. Weijian, X. Xiaoping, Z. Xiling. New Development of third harmonic ground fault protection schemes for turbine-generator stator windings. Tsinghua University. Xuchang Relay Institute. 2003. pp. 250- 253. [ Links ]
12. S. Shiwen, S. Binhua. Analysis of ground protection of unit connected generators using third harmonics. Fourth International Conference on Developments in Power Protection. UK. 1989. pp. 254-258. [ Links ]
13. D. Johnson, J. Hilburn, J. Johnson. Electric Circuit Analysis. Ed. John Wiley and Sons.Inc. New York. 1997. pp. 25-102. [ Links ]
(Recibido el 28 de abril de 2009. Aceptado el 8 de enero de 2010)
*Autor de correspondencia: teléfono: +57 + 6 +321 58 82, correo electrónico: jjmora@utp.edu.co (J. Mora-Flórez)