Formación de patrones de turing para sistemas de reacción-convección-difusión en dominios fijos sometidos a campos de velocidad toroidal

Turing pattern formation for reaction- convection-diffusion in fixed domains submitted to toroidal velocity fields

Carlos Humberto Galeano* , Diego Alexander Garzón, Juan Miguel Mantilla

Grupo de Modelado y Métodos Numéricos en Ingeniería GNUM. Universidad Nacional de Colombia, Kr. 30 No. 45-03, Edificio 453 Oficina 401, Bogotá, Colombia

---

Resumen

El presente artículo estudia el efecto de la incorporación del término de transporte en las ecuaciones de reacción-difusión de dominio fijo, a través de campos de velocidad toroidal. Se estudia específicamente la formación de patrones de Turing en problemas de difusión-advección-reacción, considerando los modelos de cinética de reacción de Schnackenberg y de glucólisis. Se analizan tres casos, los cuales se solucionan numéricamente empleando elementos finitos. Se encuentra que, para los modelos de glucólisis, el efecto advectivo modifica totalmente la forma de los patrones de Turing obtenidos con difusión-reacción; mientras que para los problemas de Schnackenberg, los patrones originales se distorsionan levemente, haciéndolos rotar en el sentido del campo de velocidades. También se logró determinar, como para valores altos de velocidad, el efecto advectivo supera el difusivo y se elimina la inestabilidad por difusión. Por otro lado para valores muy bajos en el campo de velocidad, el efecto advectivo no es considerable y no hay modificación en los patrones de Turing originales.

Palabras clave: Patrones de Turing, inestabilidad por difusión, Schnackenberg, glucólisis

---

Abstract

This article studies the effect of the inclusion of the transport term in the reaction-diffusion equations, through toroidal velocity fields. The formation of Turing patterns in diffusion-advection-reaction problems is studied specifically, considering the Schnackenberg reaction kinetics and glycolysis models. Three cases are analyzed and solved numerically using finite elements. It is found that, for the glycolysis models, the advective effect totally modifies the form of the obtained Turing patterns with diffusion-reaction; whereas for the problems of Schnackenberg, the original patterns distort themselves slightly, making them to rotate in the direction of the velocity field. Also, this work was able to determine that for high values of velocity the advective effect surpasses the diffusive one and the instability by diffusion is eliminated. On the other hand, for very low values in the velocity field, the advective effect is not considerable and there is no modification of the original Turing pattern.

Keywords: Turing patterns, diffusion instability, Schnackenberg, glycolysis

---

Introducción

Muchos problemas físicos pueden ser modelados analizando el balance de tres fenómenos: la difusión, la advección y la reacción [1]. El primero se define como la dispersión de las especies involucradas en el proceso a lo largo del dominio físico del problema. La advección se relaciona con el transporte de especies debido a la presencia de campos de velocidad. Y por último, la reacción es el proceso de interacción mediante la cual se generan o se consumen las especies involucradas en el fenómeno. La ecuación diferencial de difusión-advección-reacción involucra estos términos, tal como se expresa en (1) para un fenómeno con una sola especie.

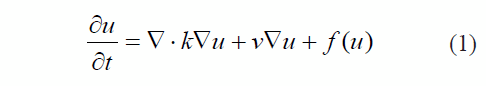
En ésta última ecuación u es la concentración de la especie estudiada, v es la velocidad asociada al fenómeno advectivo y f(u) la función que define el proceso de reacción. Esta ecuación, y más comúnmente sistemas de ecuaciones diferenciales, han sido empleados para el estudio de problemas en campos como la dinámica de fluidos [2], transferencia de calor [3-5], física de semiconductores [6], ingeniería de materiales [7], química [8], biología [9-12], dinámica de poblaciones [13-15], astrofísica [16], ingeniería biomédica [17] y matemáticas financieras entre otros.

Un fenómeno regido por los procesos de reacción y difusión, se caracteriza por la presencia de distribuciones espacio-temporales de las especies involucradas, esta distribución se denomina comúnmente patrón. Turing [18] define las condiciones para las cuales un proceso reactivo en equilibrio, puede ser inestabilizado por la presencia de un término difusivo, generándose así unos patrones espaciales heterogéneos, denominados inestabilidades por difusión o inestabilidades de Turing. De acuerdo con Turing [18], un sistema regido por la reacción-difusión de dos especies, como el definido en (2),

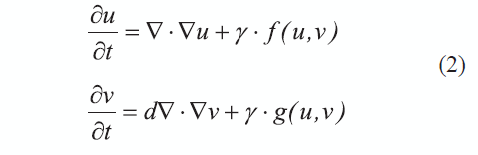
presentará inestabilidad espacial en los patrones de concentración de las especies u y v, si se cumplen cada una de las condiciones enunciadas en (3) [18-20].

En las expresiones (2) y (3), D^u y D^v son los coeficientes de los que depende la velocidad de difusión de cada sustancia en el dominio, 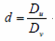es la relación entre los coeficientes de difusión de las dos especies, en tanto que γ es un coeficiente asociado con los procesos reactivos f y g. Obsérvese que se está empleando una nomenclatura con subíndices para definir las derivadas parciales.

El trabajo de Turing, permitió simular la formación de patrones en diversos procesos físicos y químicos, tales como la formación las manchas en la piel de algunos animales [10-12], [21-24], la formación de hueso, tejidos y tumores [17, 25, 26, 27], la distribución de poblaciones animales [13, 14], entre otras muchas aplicaciones.

La dinámica de la formación de estos patrones, modelada a través de las ecuaciones de reacción-difusión, es estudiada normalmente empleando diversas técnicas numéricas. Este tipo de solución se hace necesaria y útil, debido a las formas geométricas complejas de los dominios que comúnmente se tratan y a las no linealidades que se introducen en las ecuaciones diferenciales dentro de los términos de cinética de reacción clásicos, tales como los de Gierer- Meinhardt, Thomas, Schnakenberg, Gray & Scott entre otros [11]. Se han implementado soluciones al problema de reacción-difusión empleando diferente técnicas numéricas, tales como: diferencias finitas, como por ejemplo en los trabajos de Murray [22], Kondo [23], Barrio [28] y Crampin [29]; elementos finitos, como en Chaplain [27], Sekimura [30] y Madzvamuse [11, 31, 32, 33]; y elementos espectrales, como en Kassam [34]. Muchos de los estudios inicialmente desarrollados en el tema de formación de patrones de Turing, se han dedicado al trabajo con mallas fijas. No obstante, dado que muchos de los problemas físicos simulados empleando las ecuaciones de difusión-reacción implican crecimiento, algunos autores como Madzvamuse [11], han estudiado la incidencia del crecimiento de malla en la formación de patrones de difusión. En su trabajo de 2003, Madzvamuse [11], plantea un algoritmo para la solución de problemas bidimensionales de difusión-reacción empleando un dominio Euleriano continuamente creciente. En [31] se presenta una aplicación de una técnica de elementos finitos con crecimiento de malla a problemas biológicos. En 2007, Madzvamuse presenta, mediante un enfoque Lagrangiano, el efecto de una malla estructurada creciente en la formación de patrones de Turing, analizando dos técnica específicas: un método de diferencias finitas implícito y un planteamiento de elementos finitos con una discretización temporal de segundo orden semi-implícita (2- SBDF). Esté último trabajo se complementa con, en donde se comparan los resultados de la técnica 2-SBDF, con una implementación en elementos finitos que linealiza los términos de reacción.

Es de resaltar que, en los trabajos anteriormente mencionados, los cuales incorporan el efecto del crecimiento del dominio en la formación de patrones de Turing, se introduce un término advectivo en la ecuación diferencial. No obstante, en muchos de ellos el papel de este fenómeno de transporte no es evidente, debido a que el enfoque Lagrangiano empleado elimina este término de la ecuación diferencial. En otros trabajos previos, en los cuales se estudió la formación de patrones en mallas fijas, el término de advectivo no está presente.

El presente artículo se enfoca al estudio de la formación de patrones de Turing, sin crecimiento de malla, incluyendo términos advectivos con campos de velocidad toroidal. Los resultados alcanzados muestran no solo la fuerte influencia de los términos convectivos analizados con el tipo de patrón formado, sino la relación entre la magnitud del término de advectivo y la aparición o no de las inestabilidades por difusión. La estructura del artículo presentado consta de cuatro secciones: en la primera parte del texto se plantea la formulación de la ecuación de reacción-convección-difusión, mientras que en una segunda sección se presenta la solución numérica de esta ecuación a través de una formulación por elementos finitos. En una tercera sección se definen los modelos de cinética de reacción de Schnakenberg y glucólisis, en tanto que en la cuarta sección se presentan los resultados de diferentes experimentos numéricos desarrollados para dos especies, incorporando el término de transporte con campos de velocidad toroidales y los términos reactivos anteriormente mencionados. En la parte final del artículo se presentan las conclusiones.

Ecuación de reacción-advección-difusión

Se denota Ω como el dominio del problema y Γ como la frontera del mismo, en la ecuación de continuidad (4),

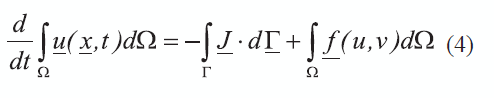
donde u = [u, v]^T, es el vector de concentración de especies, f (u, v) = [f, g]^T es el vector de funciones de reacción y J = -DVu es el vector de flujo, siendo D la constante de difusión. Para el caso de un dominio creciente con velocidad a, la ecuación de continuidad debe escribirse ahora como en (5).

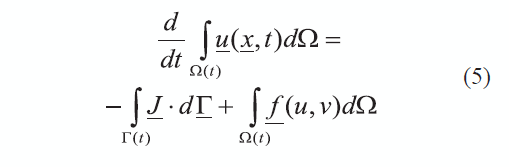
Empleando el teorema de transporte de Reynolds, el término del lado izquierdo de la anterior ecuación puede escribirse ahora como se muestra en (6).

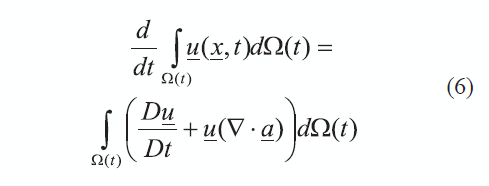
En esta última expresión Du/Dt es la derivada material del vector de concentración de especies y u(V.a) representa el término de la dilución, el cual se genera por la disminución de la concentración local cuando el volumen se incrementa, dado que V.a es la tasa local de expansión de volumen. Por otro lado, la derivada material puede escribirse como la suma de la variación de la concentración de las especies, más un término de transporte de las especies al interior del dominio, tal como se expresa en (7).

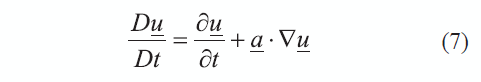
Empleando las expresiones (6), (7) y el teorema de divergencia, la ecuación de continuidad (5) se transforma en (8):

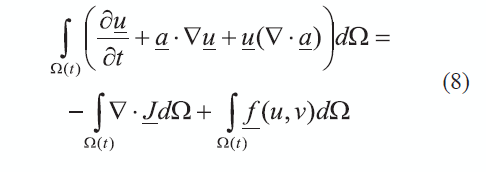
La cual puede simplificarse para obtener una expresión en forma diferencial (9):

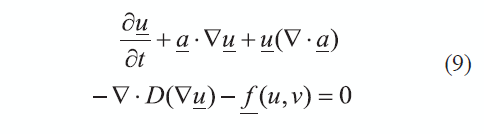
Para casos de malla no divergente como los que se pretenden estudiar en este trabajo, el término dilatante desaparece y permanece el término de transporte, así que la ecuación (9) se convierte en (10):

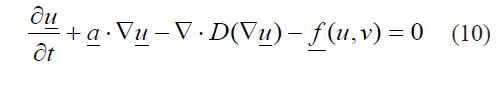
Formulación por elementos finitos de la solución de la ecuación de reacción-advección-difusión

Aplicando el método de los residuos ponderados a la expresión (10) se obtiene la ecuación (11):

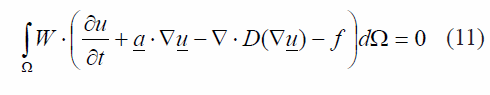
en donde W es una función de ponderación. Ahora, operando cada uno de los términos por separado e integrando por partes el término difusivo se obtiene la forma débil de la expresión (11) mostrada en (12):

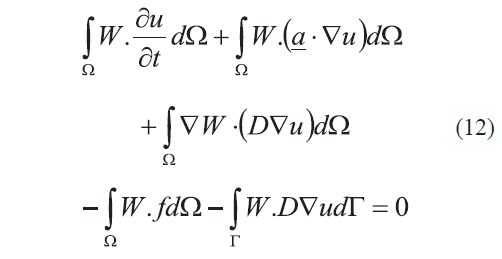
Empleando el planteamiento Bubnov-Galerkin y aproximaciones polinomiales discretas para cada elemento, tal como se muestra en (13), la ecuación de residuos ponderados puede escribirse para cada elemento como en (14) [37].

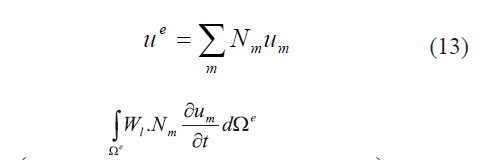
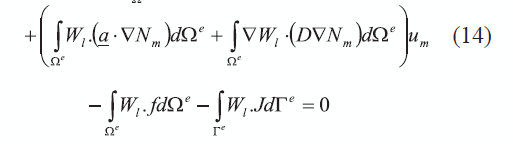
Desde el punto de vista temporal, la derivada del primer término de la expresión (14) se puede aproximar mediante un planteamiento totalmente implícito Backward-Euler, tal como se muestra en (15).

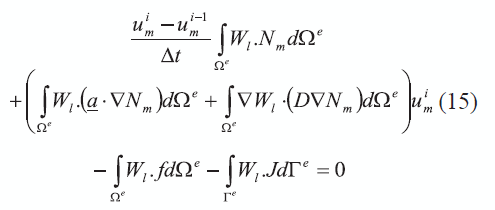
Donde uⁱ_m y u^i-1_m son los vectores de valores nodales para el instante de tiempo i e i - 1 respectivamente, en tanto que Δt es el intervalo de tiempo. En forma simplificada, la expresión (15) se puede escribir como (16):

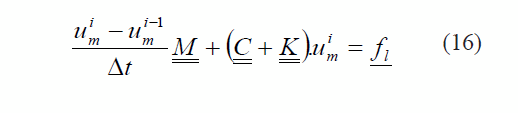
en donde los términos M, C, K y fl , se definen en (17), (18), (19) y (20), respectivamente.

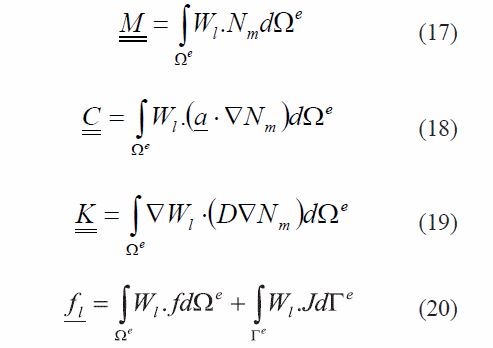
Modelo de reacción de Schnakenberg

Schnakenberg [38], consideró un conjunto de dos especies en una reacción trimolecular que admite reacciones periódicas. Este mecanismo se puede describir mediante las reacciones planteadas en (21).

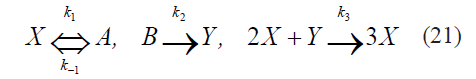
Usando la Ley de acción de masas, se pueden obtener las ecuaciones diferenciales de reacción para u y v, que son las variables adimensionales que representan las concentraciones de los compuestos o especies X y Y, respectivamente. De esta forma, las ecuaciones diferenciales de reacción para el modelo de Schnakenberg se pueden expresar como en (22),

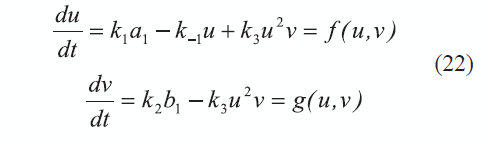
donde k_i (i = 1,1,2,3), a₁ y b₁, son parámetros positivos; en particular los dos últimos representan la concentración de A y B, respectivamente. Los términos de reacción de Schnakenberg pueden ser introducidos en un sistema de reacción- advección-difusión, que en su forma adimensional se muestra en la expresión (23).

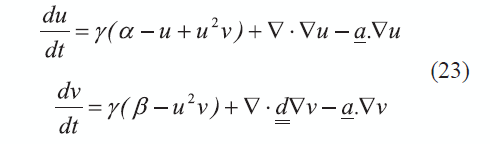
en donde las constantes positivas α y β representan la producción de u y v, respectivamente, mientras que el término de catálisis no-lineal u²v define la activación de u y el consumo de v. La constante d define la relación entre los coeficientes de difusión de cada especie. Este modelo resulta especialmente interesante debido a que su empleo en las ecuaciones de reacción-difusión permite la generación de patrones particulares generados por inestabilidades de Turing. En este proceso de formación de patrones, las pequeñas perturbaciones iniciales se amplifican y se propagan, lo que lleva a la formación de manchas que avanzan lentamente e interactúan entre sí [39]. Debido a lo anterior, el modelo del Schnakenberg es ampliamente empleado para la simulación de regeneración ósea, como en [40] en donde las especies estudiadas son las hormonas PTHrP (Hormona Paratiroidea Péptida Relacionda) y Ihh (Hormona Indian Hedgehog).

Modelo de reacción de Glucólisis

La glucólisis o glicólisis es el proceso de síntesis (oxidación) de la molécula de glucosa para proporcionar energía al metabolismo celular. A través de una secuencia de reacciones, la glucosa es transformada en piruvato y en ATP, unidad de intercambio metabólico en el organismo vivo. Este modelo de reacción, caracterizado porque las dos especies relacionadas (piruvato y ATP) pueden ejercer como generadoras o inhibidoras dependiendo de las concentraciones presentes, se emplea comúnmente para modelar los procesos de coagulación y morfogénesis [41],[42]. Las ecuaciones de reacción-advección-difusión adimensionales para el modelo de glucólisis se muestran en (24).

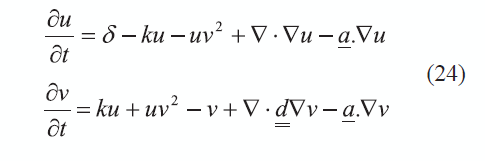
Caso 1: Modelo de difusión, advección y reacción de Schnackenberg #1

Para este modelo se definió un dominio cuadrado en coordenadas normalizadas, una constante de difusión igual a d = 8,6676, así como unas constantes de reacción de Schnackenbreg definidas por los valores mostrados en (25).

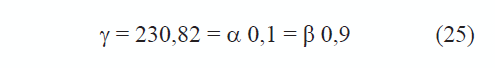
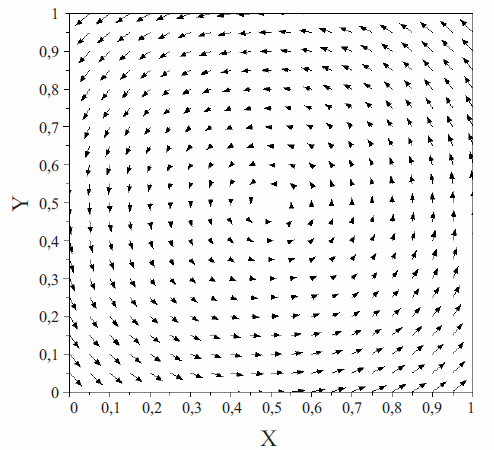
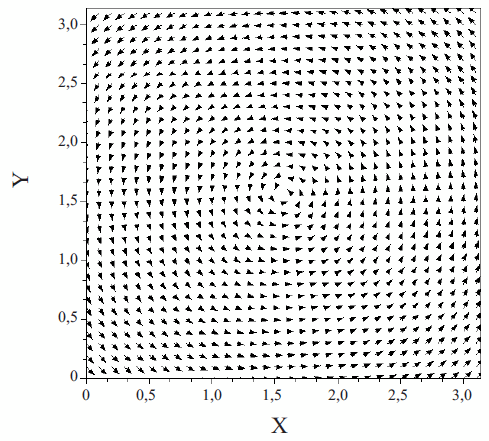
Desde el punto de vista advectivo, el campo de velocidades empleado para este problema está definido por las funciones del vector a de la ecuación (26) e ilustrado en la figura 1.

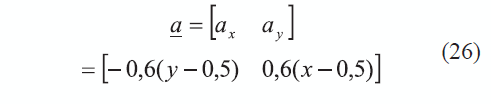
La simulación por elementos finitos realizada para este problema, utilizó una malla estructurada de 2.500 elementos (2.601 nodos) cuadrados de primer orden y un tiempo de simulación igual a 30, con incrementos de 0,01 unidades. La condición inicial se tomo como una variación aleatoria del ± 10% de la concentración de cada una de las especies alrededor del caso estable sin difusión.

Figura 1 Campo de velocidad empleado para el Caso 1

Resultados obtenidos para el Caso 1

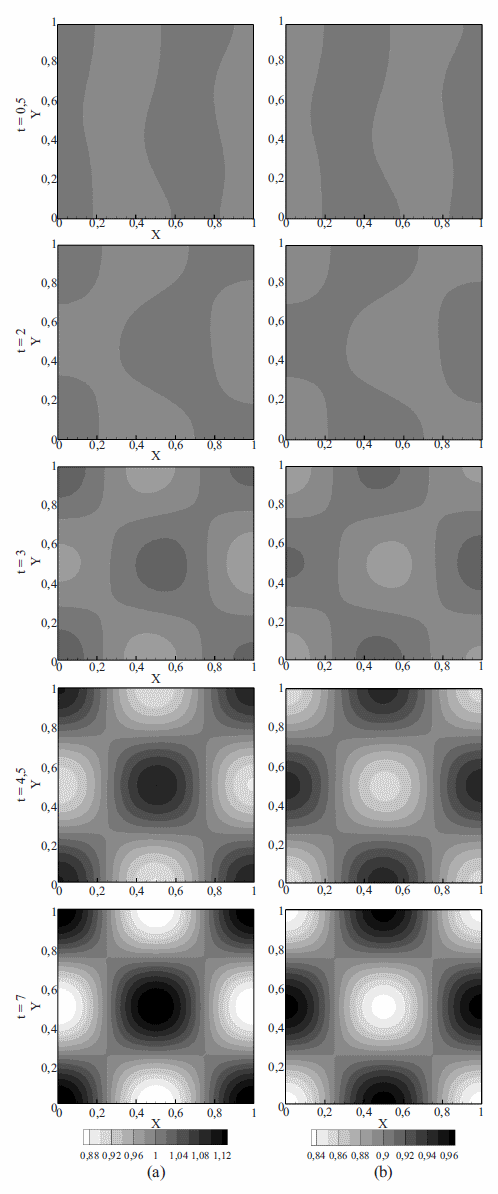
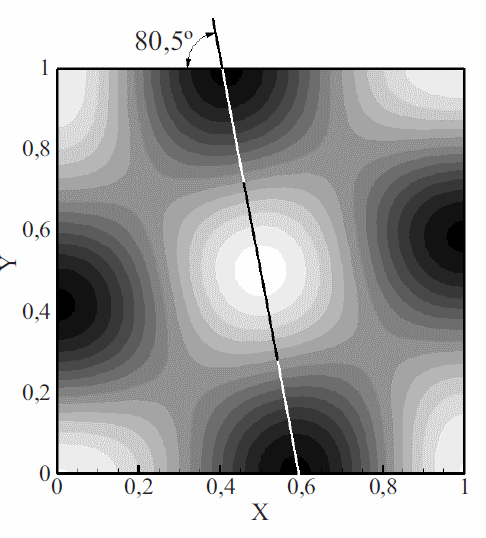
En la figura 2 se muestra los resultados de referencia obtenidos para este caso, empleando un campo de velocidad a nulo; mientras que en la figura 3 se grafican los resultados alcanzados empleando el campo de velocidad definido en (26). Para el caso de referencia, se observa la formación de un patrón de Turing semejante a un tablero de ajedrez, cuyas casillas se encuentran alineadas con los bordes del dominio. Bajo los parámetros definidos y las condiciones de estabilidad dadas en (3), el tipo de patrón espacial que se presenta, en estado estable en términos temporales, está determinado por el número de onda (2,2) [1, 20], como se muestra en la figura 2. Además se observa que el tiempo de estabilización es de aproximadamente 7 unidades adimensionales de tiempo. Por otro lado, en los resultados alcanzados adicionando el efecto de advectivo, se observa la formación de un patrón similar al anterior, aunque ligeramente distorsionado (rotado) en la dirección de giro del campo de velocidad. Esta distorsión, medida como la rotación de los puntos de más alta concentración de especie la v, es cercana a 9,5° (ver figura 4). Sin embargo este ángulo cambia para diferentes intensidades de rotación del campo de velocidad toroidal, siendo 9,5° el máximo ángulo de distorsión, pues para magnitudes de velocidad de rotación superiores a 0,6, la componente advectiva supera los efectos difusivos y no se presenta formación de un patrón de Turing. Se encuentra adicionalmente que el fenómeno de transporte introducido con el campo de velocidad, retarda el tiempo de estabilización del problema, hasta un tiempo cercano a las 30 unidades, y no modifica los niveles de concentración de las dos especies u y v.

Caso 2: Modelo de difusión, advección y reacción de Schnackenberg #2

Para la solución numérica de este caso se empleó la misma malla utilizada en el Caso 1, así como los mismos valores para las constantes definidas en (25), y se consideró un campo de velocidad toroidal oscilatorio, el cual se define en (27). En cuanto a la condición inicial, se empleó la solución del caso estable del problema reactivo.

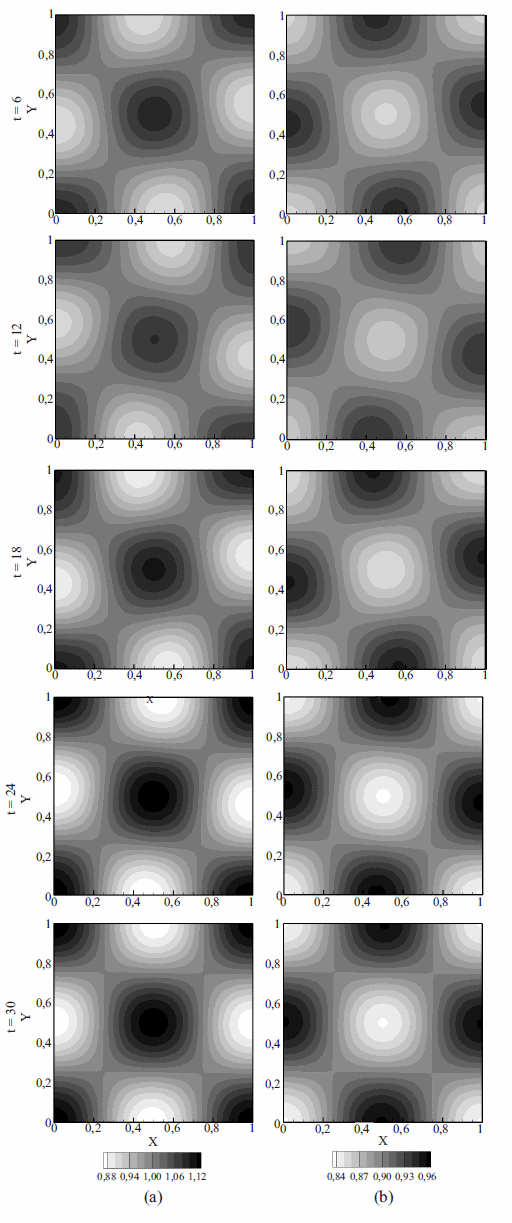
Figura 2 Distribución espacio-temporal de la concentración de los reactivos u (a) y v (b) obtenida para el Caso 1 empleando un campo de velocidad nulo (Referencia)

Figura 3 Distribución espacio-temporal de la concentración de los reactivos u (a) y v (b) obtenida para el Caso 1 empleando el campo de velocidad definido en (26)

Figura 4 Rotacion del patrón de turing obtenida para el Caso 1

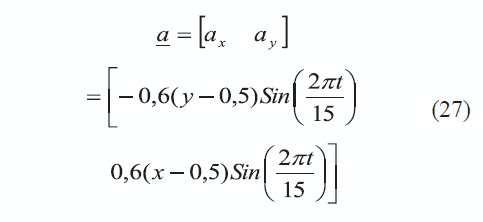
Resultados obtenidos para el Caso 2

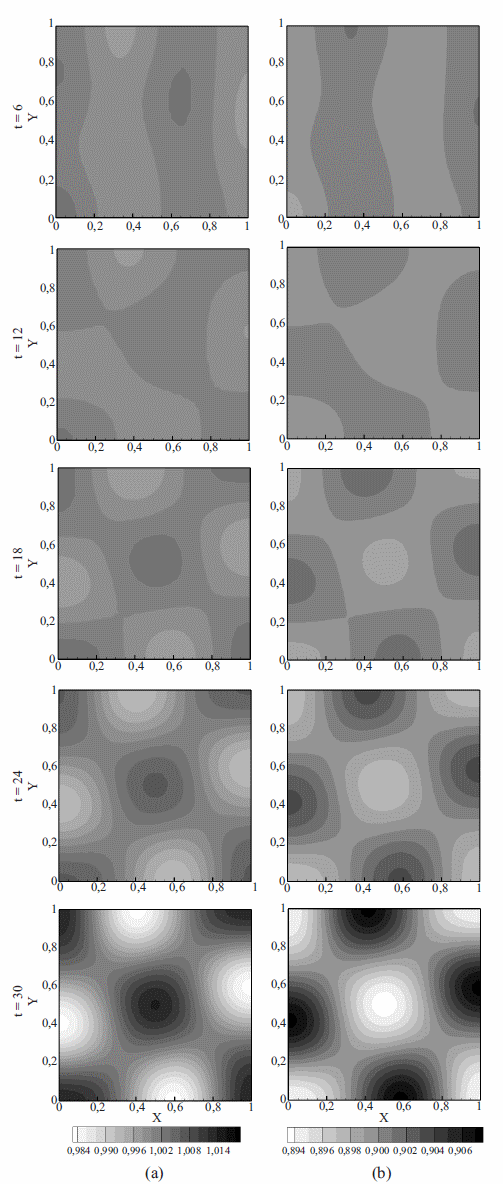
La solución obtenida, mostrada en la figura 5, presenta formación de patrones de Turing en forma de tablero de ajedrez, el cual se ve distorsionado por el sentido de giro del campo de velocidad toroidal, obteniéndose un patrón oscilatorio alrededor de la solución no advectiva o de referencia. Dado que la amplitud de la velocidad empleada fue la misma que para el Caso 1, la amplitud de oscilación del patrón resulta ser cercana también a 9,5°. No se encontró, que por efecto de este campo de velocidad oscilatorio, los niveles de concentración de alguna de las dos especies cambien con respecto al problema de referencia.

Figura 5 Distribución espacio-temporal de la concentración de los reactivos u (a) y v (b) obtenida para el Caso 2

Caso 3: Modelo de difusión, advección y reacción de glucólisis

En este caso se analiza el efecto del fenómeno advectivo en la formación de patrones de Turing, dentro de un problema con un mecanismo de reacción de glucólisis. El dominio del problema se define como un cuadrado de longitud π, discretizado con 2.500 elementos cuadriláteros lineales. El campo de velocidad toroidal empleado, con centro en 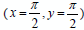, se encuentra descrito por medio de la expresión (28) (ver figura 6), en tanto que las constantes de reacción se definen en (29).

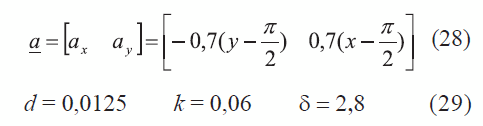
El tiempo final de simulación empleado fue de 3.000 unidades de tiempo con incrementos iguales a 0,1. La condición inicial utilizada está definida por una variación aleatoria del 10% alrededor de los valores estables del proceso reactivo.

Figura 6 Campo de velocidad empleado para el caso 3

Resultados obtenidos para el Caso 3

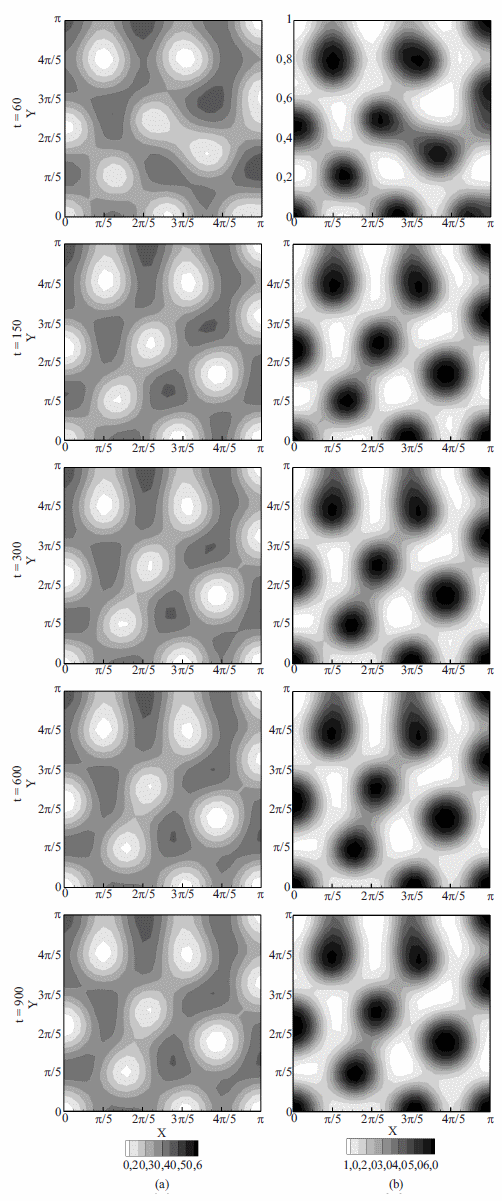
La figura 7 muestra el patrón de Turing obtenido para el problema de referencia difusivo-reactivo. Este patrón se caracteriza por la presencia de manchas en un arreglo más o menos regular, el cual se estabiliza cerca de 900 unidades de tiempo. Al adicionar el efecto de transporte, definido mediante la ecuación (28), el patrón cambia, tal como se puede observar en la figura 8.

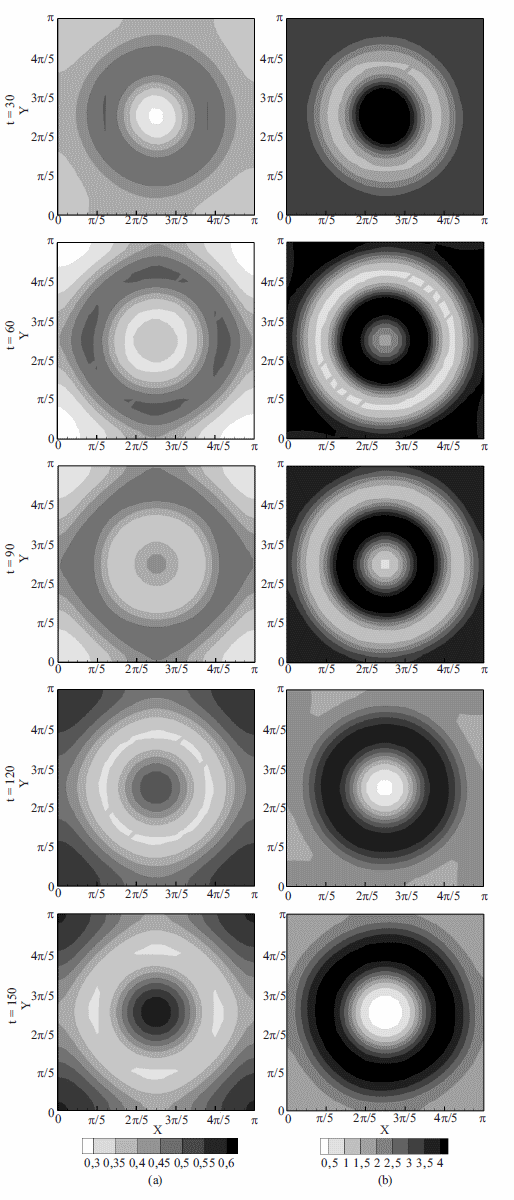
Efectivamente, el patrón de manchas obtenido en el problema difusivo-reactivo, se convierte en uno de zonas anulares concéntricas con diferentes valores de concentración. Esta distribución de concentraciones que el efecto difusivo guarda para este caso un mayor peso que la componente de transporte, de lo contrario no se observaría la presencia de patrones de Turing. A diferencia de los casos con reacción de Schnackenberg, este problema no muestra una relación evidente entre el patrón obtenido, el campo de velocidades empleado y el patrón original o de referencia. No obstante resulta claro que la inestabilidad por difusión persiste aún con la incorporación del término advectivo, además este último término cambia totalmente la forma del patrón de Turing obtenido inicialmente.

Conclusiones

Se analizaron tres problemas de difosión-advección- reacción, empleando los modelos de cinética de reacción de Schnackenberg y de glucólisis. En todos los casos se compararon los resultados de los patrones de Turing obtenidos del problema de difusión-reacción de dominio fijo y sin advección, con la distribución resultante al introducir un término de transporte por medio de un campo de velocidad toroidal. Se encontró que para los casos con cinética de reacción de Schnackenberg, en ciertos rangos de velocidad, los patrones de Turing originales se distorsionan, generándose patrones similares al inicial pero con cierto ángulo de desviación, proporcional a la velocidad de giro del campo de velocidad. Este ángulo de distorsión, para el ejemplo analizado, alcanzó un valor máximo de 9.5°, justo antes que el término advectivo lograra eliminar las inestabilidades por difusión.

Figura 7 Distribucion espacio-temporal de la concentracion de los reactivos (a) y (b) obtenida para el Caso 3 empleando un campo de velocidad nulo (referencia)

Figura 8 Distribucion espacio-temporal de la concentracion de los reactivos (a) y (b) obtenida para el Caso 3 empleando el campo de velocidad definido en (30)

Para velocidades superiores, el efecto advectivo supera el difusivo, eliminándose la inestabilidad por difusión y por tanto los patrones de Turing. En caso de emplear velocidades inferiores al rango mencionado, el efecto del transporte no es significativo y las variaciones en los patrones de Turing no son apreciables. Para los casos que emplearon el modelo de cinética de reacción de glucólisis, se encontró que el término convectivo cambia radicalmente los patrones de Turing, aún en casos de bajas velocidades de advección.

Referencias

1. D. Garzón. Simulación de procesos de reacción-difusión. Aplicación a la morfogénesis del tejido óseo, Ph.D. Thesis. Universidad de Zaragoza. 2007. pp. 10-50.         [ Links ]

2. D. White. "The planforms and onset of convection with a temperature dependent viscosity". J. Fluid Mech. Vol. 191. 1988. pp. 247-286.         [ Links ]

3. O. Hirayama, R. Takaki. "Thermal convection of a fluid with temperature-dependent viscosity". Fluid Dynamics Research. Vol. 12-1. 1988. pp. 35-47.         [ Links ]

4. M. Ardes, F. Busse, J. Wicht. "Thermal convection in rotating spherical shells". Physics of the Earth and Planetary Interiors. Vol. 99. 1997. pp. 55-67.         [ Links ]

5. J. Lir, T. Lin. "Visualization of roll patterns in Rayleigh-Bénard convection of air in rectangular shallow cavity". International Journal of Heat and Mass Transfer. Vol. 44. 2001. pp. 2889-2902.         [ Links ]

6. Y. Balkarei, A. G. Yants, Y. Rhzanov, M. Elinson. "Regenerative oscillations, spatial-temporal single pulses and static inhomogeneous structures in optically bistable semiconductors". Opt. Commun. Vol. 66. 1988. pp. 161-166.         [ Links ]

7. V. I. Krinsky. "Self-organisation". Auto-Waves and structures far from equilibrium. Ed. Springer. Berlin. 1984. pp. 111-118.         [ Links ]

8. L. Zhang, S. Liu. "Stability and pattern formation in a coupled arbitrary order of autocatalysis system". Applied Mathematical Modelling. Vol. 33. 2009. pp. 884-896.         [ Links ]

9. F. Crauste, M. Lhassan, A. Kacha. "A delay reaction- diffusion model of the dynamics of botulinum in fish". Mathematical Biosciences. Vol. 216. 2008. pp. 17-29.         [ Links ]

10. Rossi, S. Ristori, M. Rustici, N. Marchettini, E. Tiezzi. "Dynamics of pattern formation in biomimetic systems". Journal of Theoretical Biology. Vol. 255. pp. 404-412.         [ Links ]

11. A. Madzvamuse, A. Wathen, P. Maini. "A moving grid finite element method applied to a model biological pattern generator". Journal of Computational Physics. Vol. 190. 2003. pp. 478-500.         [ Links ]

12. H. Frederik, P. Maini, A. Madzvamuse, A. Wathen, T. Sekimura. "Pigmentation pattern formation in butterflies: experiments and models". C. R. Biologies. Vol. 326. 2003. pp. 717-727.         [ Links ]

13. F. Yi, J. Wei, J. Shi. "Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system". Journal of Differential Equations. Vol. 246. 2009. pp. 1944-1977.         [ Links ]

14. M. Baurmanna, T. Gross, U. Feudel. "Instabilities in spatially extended predator-prey systems: Spatio-temporal patterns in the neighborhood of Turing-Hopf bifurcations". Journal of Theoretical Biology. Vol. 245. 2007. pp. 220-229.         [ Links ]

15. B. Rothschild, J. Ault. "Population-dynamic instability as a cause of patch structure". Ecological Modelling. Vol. 93. 1996. pp. 237-239.         [ Links ]

16. T. Nozakura, S. Ikeuchi. "Formation of dissipative structures in galaxies". Astrophys. J. Vol. 279. 1984. pp. 40-52.         [ Links ]

17. A. Madzvamuse. "A Numerical Approach to the Study of Spatial Pattern Formation in the Ligaments of Arcoid Bivalves". Bulletin of Mathematical Biology. Vol. 64. 2002. pp. 501-530.         [ Links ]

18. A. Turing. "The chemical basis of morphogenesis". Phil. Trans. Roy. Soc. Lond. Vol. 237. 1952. pp. 37-72.         [ Links ]

19. E. Crampin, E. Gaffney, P. Maini. "Reaction and diffusion on growing domains: Scenarios for robust pattern formation". Bulletin of Mathematical Biology. Vol. 61(6). 1999. pp. 1093-1120.         [ Links ]

20. A. Madzvamuse. A numerical approach to the study of spatial pattern formation. Ph.D. Thesis. University of Oxford. Oxford. 2000. pp. 10-147.         [ Links ]

21. H. Meinhardt. Models ofBiologicalPattern Formation. Ed. Academic Press. London. 1982. pp. 53-58.         [ Links ]

22. J. Murray. "A prepattern formation mechanism for animal coat markings". J. Theor. Biol. Vol. 88. 1981. pp. 161-199.         [ Links ]

23. S. Kondo, R. Asai. "A reaction-diffusion wave on the skin of the marine anglefish, Pomacanthus". Nature. Vol. 376. 1995. pp. 765-768.         [ Links ]

24. T. Sekimura, A. Madzvamuse, A. Wathen, P. Maini. "A model for colour pattern formation in the butterfly wing of Papilio dardanus". Proc. Roy. Soc. London. Vol. 26. 2000. pp. 851-859.         [ Links ]

25. J. García-Aznar, J. Kuiper, M. Gómez-Benito, M. Doblaré, J. Richardson. "Computational simulation of fracture healing: Influence of interfragmentary movement on the callus growth". Journal of Biomechanics. Vol. 40. 2007. pp. 1467-1476.         [ Links ]

26. S. Ferreira, M. Martins, M. Vilela. "Reaction-diffusion model for the growth of avascular tumor". Physical Review. Vol. 65. 2002. pp. 1-8.         [ Links ]

27. M. Chaplain, A. Ganesh, I. Graham, "Spatio-temporal pattern formation on spherical surfaces: Numerical simulation and application to solid tumor growth". J. Math. Biol. Vol. 42. 2001. pp. 387-423.         [ Links ]

28. R. Barrio, C. Varea, J. Aragón, P. Maini. "A two- dimensional numerical study of spatial pattern formation in interacting systems". Bull. Math. Biol. Vol. 61. 1999. pp. 483-505.         [ Links ]

29. E. Crampin, E. Gaffney, P. Maini. "Reaction and diffusion on growing domains: Scenarios for robust pattern formation". Bull. Math. Biol. Vol.61. 1999. pp. 1093-1120.         [ Links ]

30. T. Sekimura, A. Madzvamuse, A. Wathen, P. Maini. "A model for colour pattern formation in the butterfly wing of Papilio dardanus". Proc. Roy. Soc. London. Vol. 26. 2000. pp. 851-859.         [ Links ]

31. A. Madzvamuse, A. Wathen, P. Maini. "A moving grid finite element method for the simulation of pattern generation by Turing models on growing domains". J. Sci. Comp. Vol. 24 . 2005. pp. 247-262.         [ Links ]

32. A. Madzvamuse, R. Thomas, P. Maini, A. Wathen. "A numerical approach to the study of spatial pattern formation in the ligaments of arcoid bivalves". Bull. Math. Biol. Vol. 64. 2002. pp. 501-530.         [ Links ]

33. A. Madzvamuse, T. Sekimura, A. Wathen, P. Maini. "A predictive model for colour pattern formation in the butterfly wing of Papilio dardanus". Hiroshima Math. J. Vol. 32. 2002. pp. 325-336.         [ Links ]

34. A. Kassam, L. Trefethen. "Solving reaction-diffusion equations 10 times faster". Numerical Analysis Group Research Report No. 16. Oxford University. Oxford. 2003. pp. 1-13.         [ Links ]

35. A. Madzvamuse, P. Maini. "Velocity-induced numerical solution of reaction-diffusion systems on continuosly growing domains". Journal of computational physics. Vol. 225. 2007. pp. 100-119.         [ Links ]

36. A. Madzvamuse. "Time-stepping schemes for moving grid finite element applied to reaction-diffusion systems on fixed and growing domains". Journal of computational physics. Vol. 214. 2006. pp. 239-263.         [ Links ]

37. O. Zienkiewicz, R. Taylor. Problemas de convección dominante: Aproximaciones de elementos finitos a la ecuación de difusión-advección. Finite Element Method. Ed. Butterworth-Heinemann College. Oxford. Vol. 3. 2000. pp. 5-150.         [ Links ]

38. J. Schnakenberg. "Simple chemical reaction systems with limit cycle behaviour". J. Theor Biol. Vol. 81. 1979. pp.389-400.         [ Links ]

39. R. Revelli, L. Ridolfi. "Generalized collocation method for two-dimensional reaction-diffusion problems with homogeneous Neumann boundary conditions". Computers and Mathematics with Applications. Vol. 56. 2008. pp. 2360-2370.         [ Links ]

40. D. Garzón Alvarado, J. García-Aznar, M. Doblare. "A reaction-diffusion model for long bones growth", Biomechanics and modeling in mechanobiology. Vol. 8. 2009. pp. 381 - 395         [ Links ]

41. D. Garzón Alvarado, J. García-Aznar, M. Doblare. "Appearance and location of secondary ossification centres may be explained by a reaction-diffusion mechanism". Computers in biology and medicine. Vol. 39. 2009. pp. 554-561.         [ Links ]

42. J. Vanegas, N. Landinez, D. Garzón-Alvarado. "Análisis de Inestabilidad de Turing en Modelos Biológicos". Revista DYNA. Vol. 76. 2009. pp. 123-134.         [ Links ]

(Recibido el 19 Febrero de 2009. Aceptado el 15 de febrero de 2010)

*Autor de correspondencia: teléfono: +57 +1 + 316 50 00 ext. 14062, fax +57 +1 + 316 53 33, correo electrónico: chgaleanou@unal.edu.co (C. Galeano).