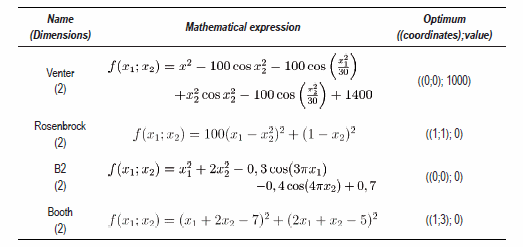Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230versão On-line ISSN 2422-2844
Rev.fac.ing.univ. Antioquia n.53 Medellín jul./set. 2010
Topology effect of two PSO and simplex hybrids
Efecto de la topología de dos híbridos del PSO con el simplex
Rodrigo Correa1*, Julio Carrillo2, Oscar Reyes1
1Escuela de Ingenierías Eléctrica, Electrónica y de Telecomunicaciones, Universidad Industrial de Santander, Ciudad Universitaria, Carrera 27 - Calle 9, Apartado Aéreo 678, Bucaramanga, Santander, Colombia
2Escuela de Matemáticas, Universidad Industrial de Santander, Ciudad Universitaria, Carrera 27 - Calle 9, Apartado Aéreo 678, Bucaramanga, Santander, Colombia
Abstract
This paper shows optimization results for a group of standard functions. When the optimization algorithm PSO is hybridized with the simplex traditional algorithm (SX, Nelder-Mead) in two different ways, i. e. the alternating interaction hybrid (PSOSX(AIH)) and the parametric evolution hybrid (PSOSX(PEH)), markedly noticeable effects are observed in both the computing time and the accuracy and precision of their results during the optimization process.
Keywords: Optimization, particle swarm optimization, simplex, hybrids
Resumen
En el presente artículo se muestran los resultados de optimización, utilizando un grupo de funciones estándar. Al hibridizar el algoritmo de optimización PSO (Particle Swarm Optimization) con el algoritmo simplex tradicional (SX, Nelder-Mead) de dos formas diferentes, esto es, el híbrido de interacción alternante o secuencial (PSOSX(HIA) ) y el híbrido de evolución paramétrica (PSOSX(HEP)), se observan efectos marcados en sus tiempos de cómputo y en la exactitud y precisión de la respuesta durante una operación de optimización.
Palabras clave: Optimización, enjambre de partículas, simplex, híbridos
Introduction
The PSO algorithm as optimization strategy makes part of the so denominated evolutionary computing whose development seems to have been strengthened by the observation of natural phenomena, the social and individual behavior of animal species among which we find bees, ants, birds and most recently cockroaches, [1-4]. This method has rapidly evolved due, among other things to the varied and ever-demanding applications in which it has shown its worth; being largely welcomed in the academic community most likely by the simplicity of the algorithm and by its efficiency in the search of the global optimum in a great variety of optimization problems with or without restrictions. PSO was born in 1995 and as today there is an innumerable quantity of variants that make it full of features, as guaranteed convergence, usage ease in discontinuous search spaces and parallel programming, among other abilities [5-7]. The first text fully dedicated to PSO, as far as we know, only appeared in 2006 [8], though the initial version of this PSO algorithm came into existence llyears earlier, [9]. Proof of its unprecedented diffusion is clearly seen on the internet; there are now hundreds of thousands of virtual pages, some really good, where the PSO algorithm and its new modifications are explained. Similarly, there were approximately 89 doctoral dissertations as of October 2008, and 144 as of May 2009, related to its applications to different fields of knowledge, [10]. Likewise, on the internet several virtual meeting sites dedicated to report work on this field can be easily found which allow people to stay up-to-date and in direct contact with the people and groups that tackle this issue. Furthermore, there is scientific literature about reports from researchers that have matched the PSO algorithm with other algorithms of artificial intelligence, [11]. The current article is closely related with two optimization algorithms the result of hybridizing the original PSO with the already known SX, without restrictions optimization method of the 60's [12]. Although both algorithms have been reported in the scientific literature in an independent way, there is not any comparative study, [13,14]. In this article their particular topology is defined and the results of several simulations are compared by using four functions typically found in the evaluation of optimization algorithms because they have a given level of difficulty for the location of their global optimum. As far as computing time and accuracy is concerned, the existence of a clear difference between them is proved in spite of the fact that they both are the result of hybridizing the same algorithms, that is, the PSO algorithm and the SX method, and the fact that one of them is strongly dependent on the initial conditions. These aspects are discussed in the following sections.
Fundamentals
In this section some concepts related with the SX method, the original PSO and with two of the possible hybrids of the latter are included. Given the fact that the SX is such a widely known algorithm in the optimization process of functions without restrictions and the fact that it has been modified by several authors throughout the time, it will not be presented in detail, making the corresponding referrals, [12]. However, it will be described in order to make it easier for the reader to remember this simple but very effective algorithm. It is good to keep in mind that the large majority of commercial computing programs already feature this algorithm as a basic routine. This method is classified as one of optimization of local search for functions without restrictions whose gradient is unknown; it requires the supposition of the initial points of the object function to get started. Then it is assumed that if there is not enough information for the appropriate selection of these points, the risk of not finding the optimum value increases. This method has another weakness which lies in the fact that a minimum or maximum can be found, but there is no guarantee it is the global optimum we are looking for, since it only uses local information and in the case of stationary points, its convergence can be seriously at stake.
The algorithm performs several operations with geometric (vectorial) interpretations evaluating a function of N variables and initially creating a figure denominated simplex in N dimensions that have N + 1 vertices. The objective function is measured at each of those points. Once the start points are ready, which for the case of two dimensions are three, we can proceed to calculate the objective function at each of those points (vertices); the algorithm progresses in sequence classifying, at each iteration, these evaluations in the objective function as the optimum, the good one, and the worst. In parallel the best descending direction is selected (minimization) based on several rules pre-established [12]. At the end of the iterations, the minimum of the function is expected to be achieved. On the other hand, the PSO algorithm classified within the great family denominated swarm intelligence was created by Eberhart and Kennedy and was born as a modeling tool during the study of social behavior of some animal species, [9]; it is considered as an evolutionary meta-heuristic strategy. Since its conception and given its heuristic nature no further explanation or mathematical fundamentals were proposed and its authors clearly established that many of its results that in the end formed this algorithm were basically obtained by trial and error techniques. As time went by, approximately 14 years, and with the participation of several researchers, the original algorithm started to evolve over time to become currently available in a large quantity of variants, [2]. Clerc [8] pointed out, three years after the reporting of the creation of the PSO algorithm, some facts that became noteworthy in the discussion leading to facilitate the diffusion of this method in the engineering field; its analogy with a spring-mass system and the representation in space of states in both sides, the one related with mathematical aspects that were useful to define a factor that could, in most cases, guarantee its convergence. This algorithm features the following: Evolutionary by nature and based on a population of particles, it requires to be initialized with a population of random solutions, it searches for the optimum both locally (sub-domains) and globally, it features a memory in terms of a weight factor or variable inertia over time, it sets forth the interchange of information based on cognitive and social coefficients, it is a non-linear method of optimization that does not require you to know the derivatives of the objective function. It is applied to problems with objective functions without restrictions and it is valid for both continuous and discreet problems (modified PSO).
The algorithm
The algorithm starts from the hypothesis that each particle (point within the domain of the objective function that is set forth as a possible solution) is "thrown into flight", as some authors describe, into the search space (swarm of N particles) guided by the particle that has so far found the best solution and that works as the leading function of the swarm. The particles evolve bearing in mind the best solution found in their path and in that of the leader. The proceeding also takes into account the best value reached by some of the surrounding particles. In each iteration, the particles modify their speed towards the best surrounding solution considering the information from the leader. For the reader eager to know the details of the interpretation from a Newtonian point of view of mechanics, which wasn't exactly the initial interpretation, might go over the given references, [6,7,10]. Either in this way or as proposed by Eberhart and Kennedy, we get to the same two expressions that wrap up the original PSO for a particle which needs vectorial notation to be applied to the swarm as a whole. Therefore, the particles evolve according to the following set of matrix-based equations rendering the original PSO algorithm expressed as follows:
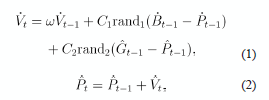
in which each one of its components represents: Vt the velocity matrix M x N of each particle in time t; w the inertia factor; Vt-1 the velocity matrix M x N of each particle in time t - 1; C1 the cognitive parameter; rand1 an independent random number with uniform probability between 0 and 1; Bt-1the matrix M x N storing the best position of each particle in time t -1 (best individual position); Pt-1 the matrix M x N storing the best position of each particle in time t - 1; C2 the social parameter; rand2 an independent random number with uniform probability between 0 and 1; Gt-i the matrix M x N storing the best position achieved by the swarm in time t-1 (the best position of the leader), and Pt the matrix M x N storing the position of each particle in time t. In order to program this algorithm, the variable change t = k + l is made.
The PSO and SX hybrids
Given the flexibility of the original PSO algorithm, it is possible to hybridize it with other optimization strategies in order to achieve more precise results, without sacrificing either computing time or precision. It is interesting to find out how hybridization though performed through the very same method, that is, the SX method, can certainly be made in at least two ways which is basically the core of the present article; The Alternating Interaction Hybrid (AIH) and the Parametric Evolutionary Hybrid (PEH). Each one it is explained as follows:
The alternating interaction hybrid (AIH)
In this hybrid, at the end of each iteration of the PSO algorithm, the SX method is used staring from the solutions set obtained in such iteration, in order to get a better local solution; the next iteration with the PSO algorithm begins with the solutions set improved by the SX method, and so on and on. Given this calculus scenario, it is expected to get a better solution that entails a not very high cost of computing time which has to be estimated for each application in particular. A hybrid application like this was reported in [13], in the design of an adaptive recurrent fuzzy controller embedded in a FPGA (Field Programmable Gate Array), to be used in water tank's temperature control; it was used specifically in the controller's off-line training phase. In their article, the authors assume for the weight factor w a unit value and 0.8 for the convergence factor. Independently from using a numeric algorithm such as the SX method, this kind of hybrids do not lose their heuristic features, since they require the selection of a set of parameters obtained through trial and error valid for the particular conditions of the problem.
Parametric evolutionary hybrid, (PEH)
One of the objectives of this hybrid algorithm PSOSX(PEH), is to incorporate an auto-configured search strategy that guarantees the optimum (or the quasi optimum) of the parameters of the PSO algorithm through the SX method, in such a way that it assures success in the independent search of the particularities of the problem studied. The central idea of this hybrid lies in the fact that the SX method algorithm can select the values of the parameters (N,w,C1, C2) contained in the space of parameters so that they ensure an almost optimum configuration for the PSO algorithm to perform the evaluation of the objective function in each iteration. Within this heuristic, each vertex of the SX method remains defined by the coordinates (N,w,C1, C2). In this point the PSO algorithm takes the values of the heuristic parameters determined by the SX method and validates the objective function according to the equations (1) and (2). Consequently, each point found by the SX method, product of any reflection, contraction, expansion or reduction, is defined by an independent exam characterized by the vector Xi(Ni,wi,Ci1,Ci2), i = 1,...,m + 1, where m is the number of parameters of the PSO algorithm and Ni is the whole number that represents the swarm's size. This last variable was included in order to estimate its optimum value. This proceeding, hypothetically, improves the PSO algorithm's search capacity and besides that, it makes the heuristic parameters independent due to the fact that it performs a search directed by almost optimum parameters automatically. In the following section, a series of computing tests are included leading to compare the relative performance of this two hybrids by using various functions whose optimum is known in advance.
Experimental evaluation
In this excerpt only the results with the two hybrids are reported leaving aside the simulations with other variants of the PSO algorithm. In the same manner only a few results are reported since various dimensions, functions and numbers of iterations were used. In order to evaluate both computing time and accuracy for the hybrid algorithms PSOSX (AIH) and PSOSX (PEH), four functions were selected whose equation and optimal value are theoretically known. These equations appear on table 1.
Table 1 Selected functions for hybrid-testing
In the first series of tests, the number of iterations was changed, leaving C1 = C2 = Cab = 2.0 and w = 1.0. Then, the same type of testing was performed on the two hybrids, that is, keeping the number of initial iterations in two and later in 35. After that, the respective error values, standard deviation, and the mean were tabulated. To finish, a second test was made leaving the number of iterations constant, and changing Cab and w. For this case, the same results analysis was made as in the first series. The results for two functions are presented below, but the results for the four functions selected for this study are resumed in the conclusions section. All the experiments were carried out using a DELLTM INTEL Core 2 DuoTM 2GHz computer, having Windows VistaTM as the operative system.
Experiments changing the number of iterations
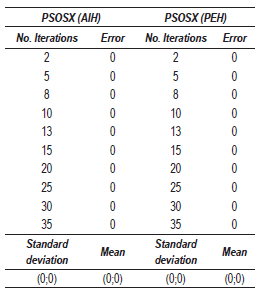
Venter function
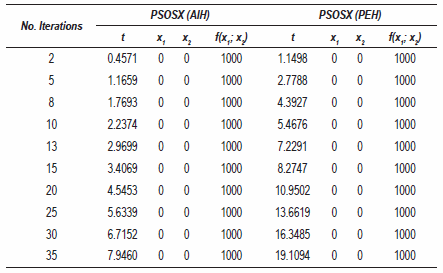
For this function, see table 2. The difference in computing time in the two hybrids is noticeable, basically because its difference increases without a visible factor; as the iterations increase, the two hybrids reach the same optimum value.
Booth function
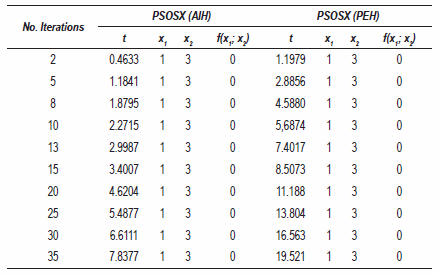
It is noticeable that even for a few iterations, table 3, the best global of each topology shows the exact response of the function. This can be attributed to the fact that the optimum of this function is easily differentiated, there are no local minimum or maximum values near the optimum the origin. Once again, the optimization time of that may interfere in the search process, and the PEH hybrid is quite greater than that of the because the initial location of the particles is near AIH hybrid.
Table 2 Optimization of the Venter function, time t is in seconds
Table 3 Optimization of the Booth function, time t is in seconds
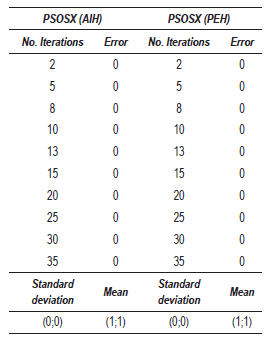
Rosenbrock function
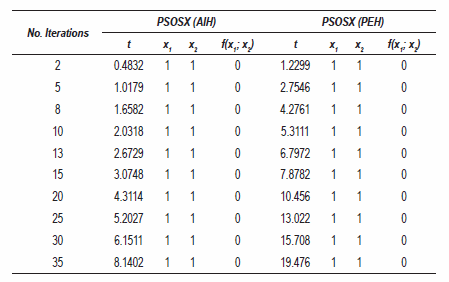
The results shown on table 4 are similar to those found on the previous table, possibly due to the fact that the Rosenbrock function's difficulty level is similar to that of the Booth function, for which, the behavior of the hybrids was quite similar.
Table 4 Optimization of the Rosenbrock function, time t is in seconds
Analysis of the generated response
The main results of the optimization of these functions are presented below, but emphasizing on the response's error in relation to the optimum known in advance; likewise, the standard deviation, and the mean of the coordinates of the independent variables that correspond to the optimum found are presented.
Venter function
As it was expected in the Venter function, the absolute error of the hybrid is zero, because in all cases, the exact response to the optimization problem was found. The results shown have a standard deviation of zero in both cases, mostly due to the fact that the responses did not change in all the tests presented on tabla 5. For the case of the mean, it is zero because all the values found in the tests were zero. It is good to point out that on the following tables the values that appear on the last row were applied to the coordinate set (x1; x2) reported by the hybrids and that correspond to the position of the global optimum.
For the Booth function, the mean had the value of 1 for x1, and, 3 for x2, which are the coordinates where the global optimum of the function is found.
Table 5 Optimization of the Vender function
Rosenbrock function
The results of table 6 are similar to those found for the rest of the functions, with the only difference that for this case, the optimum of the Rosenbrock function is found at the point 1;1, thereof, the values of the mean in both hybrids reach such value.
Table 6 Optimization of the Rosenbrock function
Variation of parameters Cab and w
Next, some other tests were run keeping the number of iterations fixed and at a value of 8, and then the parameters Cab and w were varied.
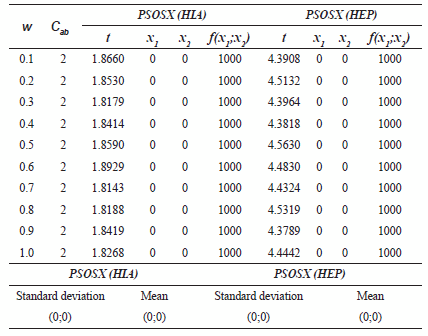
Venter Function
For this type of test, see table 7, the value of Cab remained constant and equal to two, and w was varied; a slight decrease in the response times was observed specially in the case of PSOSX(PEH), bearing in mind that the maximum number of iterations allowed was 8. The values of the mean, the standard deviation did not change, given the fact that the global optimums were found.
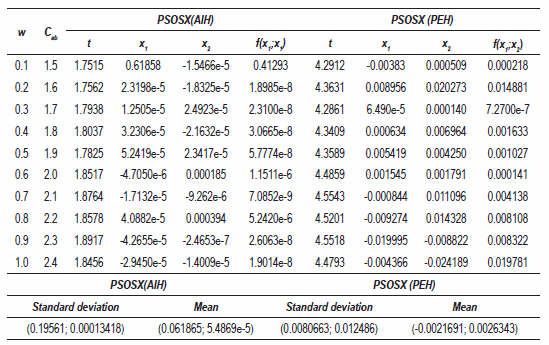
Function B2
The data of table 8 show the effect of changing both parameters. Although the values of f(x1;x2) are very close to zero, it is clearly seen that for some values of these parameters, the response drastically changed in each hybrid in different ways.
Table 7 Optimization of the Venter function changing w and keeping Cab constant. Time t is given in seconds
Table 7 Optimization of the function B2 changing w and Cab. Time t is in seconds.
In the results of the PSOSX(AIH), it is observed that for w = 0.6 and Cab , = 2.0, the value of f(x1;x2) noticeably changed with respect to the other values; pretty much the same happens when w = 0.8 and Cab , = 2.2. These records are approximately 20 times larger than the rest, showing in this way a noticeable difference when it comes to the quality of the response. By analyzing the results of the PSOSX(HPE), it is quite evident that for w = 0.3 and Cab = 1.7, the value of f(x1;x2) became more precise and accurate (within 10-7). These results prove that for each of these topologies, the start parameters should do not be necessarily the same because due them, each hybrid becomes more efficient (faster) searching for the answer to the problem. Once the tests were concluded with the four selected functions, it was observed that for some of them (peculiarly function B2) the responses to the optimization process were affected by the variations of these parameters. This is leading to conclude that the parameters Cab and w are neither the optimal values nor the same for both hybrids and it leads to the thought that for each typology and problem, these initial values are determining factors when it comes to finding a response that complies with the necessary requirements of accuracy and reproducibility in a requested computing time.
Comparative analysis of the hybrids
In this section and as a demonstrative example, the graphic that appears on the left shows the results with the hybrid PSOSX(AIH), and to the right those with the hybrid PSOSX (PEH).
Venter function, 2D
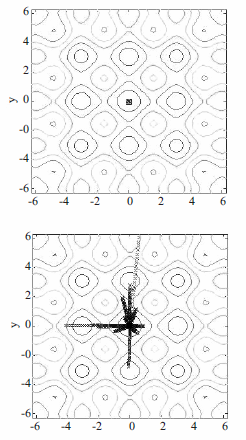
Now by using 35 itinerations, figure 1, it is seen how the hybrids get closer tp the optinum. In the PSOSX(PEH) case, for example, the track of the particles getting closer to the response can be seen. This snapshot shows how the PSOSX(AIH) could make all of its particles reach the optimum in contrast with the PSOSX(PEH).
Figure 1 Hyrbids optimizing the Venter function, history of 35 iterations; the search space was [-6;6]. (a) PSOSX(HIA), (b) PSOSX(HEP)
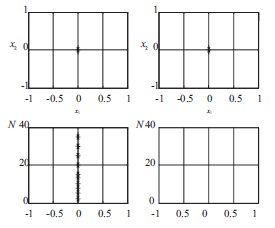
In figure 2 six graphics are observed that compare the results of the optimization process of the two hybrids for this function. In such figure the location of the solutions found stands out for each hybrid, which overlap the origin. This figure consolidates the location of the coordinates of the optimum, the distance in function of the number of iterations and also in function of computing time. Distance was defined as the difference between the experimental solution and the theoretical solution previously known. It is observed that the optimum of the function obtained through the use of PSOSX(AIH) (left side of the figure), is in position (1;1); from the number two iteration of 35 preset, it was found and it took an average of 7.5 seconds. Likewise, the PSOSX(PEH) (right side of the figure) found the same coordinates in eight iterations, but it took an average of 20 seconds. The parameters Cab = 2.0 and w = 1.0 were set; the population size was 50 particles and the search space remained in an interval of [-6;6].
Figure 2 Hybrids optimizing the Venter Function, 35 iterations; search space was [-6;6]. N is the number of iterations and t is time in seconds. (a) PSOSX (HIA), (b) PSOSX (HEP)
Function B2
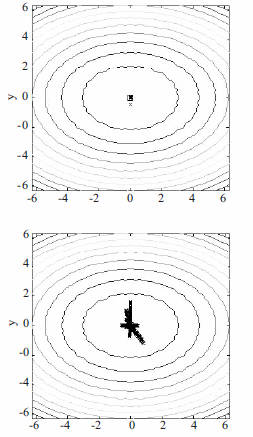
On the other hand when this function and the two hybrids were used, once again the dispersion of particles in the search space [-6;6] was revealed by the end of the optimization process when the maximum number of iterations was two. Now, when the number of iterations is increased to 35 (figure 3), it indicates it is an appropriate number given the excellent location of the function's optimum.
In a more detailed analysis, it was observed how with both hybrids the optimum was reached but the catch of some particles still lingering in values relatively distant to it, that is, by the end of the 36 iterations, there is a number of particles located in points that do not relate to the global optimum.
Figure 3 Displacement of particles towards the optimum with the hybrids PSOSX (AIH) and (PEH) optimizing function B2, 35 iterations. (a) PSOSX (HIA), (b) PSOSX (HEP)
Analysis and conclusions
The PSOSX hybrids proved excellent accuracy, precision and robustness (reaching the global optimum in all of the problems that they were applied to). The experimental results revealed that hybrid algorithms, that is, the PSOSX(AIH) and the PSOSX(PEH) surpass the basic algorithm, so generating good quality solutions. The number of iterations plays an important role when accuracy and precision in the answer is required; as the number of iterations increase, greater precision is obtained, but also longer computer time is required. From the tests conducted, it was observed that the initial values of the parameters (Cab and w), notably influence optimum search process of the function as in any other numerical method, but it was also observed that there are appropriate values these parameters have for each hybrid. This leads to the conclusions that despite using any value for these parameters (obviously within the predetermined ranges), good results are achieved, but there are better values for each hybrid and perhaps for each problem to tackle. One point that must be considered worthy of attention and is related to both hybrids is the computational performance of the SX method (Nelder-Mead); for the studied cases it was observed that if the initial particles are way too dispersed, the computing time, and the quality of the response are adversely affected. It was observed that the PSOSX(AIH) can find answers with better accuracy and precision more quickly that the PSOSX(PEH), as long as the necessary iterations are conducted so the Simplex can converge efficiently. The excessive increase in the number of particles for each dimension consequently brought around the increase in the computing time of the initial positions, making the search inefficient. This observation had a contrast with the hypothesis that the possibility of finding the answer quickly improves if there are more particles in the space, therefore fewer iterations and less time are required. The PSOSX(PEH) has a greater advantage over the PSOSX(AIH), in the sense that if inappropriate initial values are introduced, the Simplex can correct that mistake and so increase the efficiency of the basic PSO avoiding its divergence. All this brings around possible consequences of course, such as prolonged computing times. Through the proposal of the new PSOSX(PEH) topology, it was concluded that it is certainly an effective tool in cases where "time is not a key issue", such as projects that do not need an immediate answer but do need accuracy as a must. The stop criterion used for the computational tool was the comparison among the global best consecutives where the tolerance among them had to be less than or equal to 10%. Though there are other stop criteria that were discarded, it was observed how the criterion of the maximum number of iterations ended up wasting time in cases where just 8 or fewer iterations were enough to achieve the global optimum values. By comparing the results obtained for all the trial functions, it can be finally concluded that PSOSX(AIH) can reach answers of better quality (accuracy and precision) than those of PSOSX(PEH) in almost half of the time, aspect that sets the difference when it comes to complex problems in which computing time and the use of resource are a constraint.
References
1. F. Chan, M. Kumar. "Swarm intelligence". Focus on ant and particle swarm optimization. Ed. I-Tech Education and Publishing. Vienna. Chap. 7. 2007. pp. 111-139. 2. F. Van den Berg. An analysis of particle swarm optimizers. Ph.D. Thesis. University of Pretoria. Pretoria. 2002. pp. 1-135. [ Links ] [ Links ]
3. A. Moraglio, C. Di Chio, J. Togelius, R. Poli. "Geometric Particle Optimization", J. of artificial Evolution and Applications. Vol. 1. 2008. pp. 1-14. [ Links ]
4. T. Havens, C. Spain, N. Salmon, J. Keller. "Roach Infestation Optimization". IEEE Swarm Intelligence Symposium. St. Louis (MO). 2008. pp. 21-23. [ Links ]
5. A. Carlisle. Applying the particle swarm optimizer to non-stationary environments. Ph.D. Thesis. Auburn University. Auburn (USA). 2002. pp. 1-120. [ Links ]
6. J. Nanbo. Particle swarm optimization in engineering electromagnetic. Ph.D. Thesis. University of California. Los Angeles (CA). 2008. pp. 1-135. [ Links ]
7. K. Byung. Parallel algorithms for biomedical optimization problems. Ph.D.Thesis. University of Florida. Gainesville (FL). 2005. pp. 1-167. [ Links ]
8. M. Clerc. Particle Swarm Optimization Ed. Prentice Hall. Chippenham (Great Britain). Chapter 4. 2006. pp. 69-79. [ Links ]
9. J. Kennedy, R. Eberhart. "Particle Swarm Optimization". Proc. IEEE Int. Conf. Neural Networks. Piscataway (USA). 1995. pp. 1942-1948. [ Links ]
10. http://proquest.umi.com/pqdweb. Databases ProQuestMR. Consultado el 8 de mayo de 2009. [ Links ]
11. A. Lazinica. Particle Swarm Optimization, Ed. InTech. Vienna (Austria). 2009. pp. 1-486. [ Links ]
12. J Nealder, R. Mead. "A Simplex method for function minimization". Computer Journal. Vol.7.1965. pp. 308-313. [ Links ]
13. F. Chia, C. Hsu. "Temperature control by chip implemented adaptive recurrent fuzzy controller designed by evolutionary algorithm." IEEE Transactions on circuits and systems. Vol. 52. 2005. pp. 2376-2384. [ Links ]
14. S. Shu-Kai, E. Zhara. "A hybrid simplex search and particle swarm optimization for unconstrained optimization". Euro. J. of Operational Research. Vol. 2. 2007. pp. 527-548. [ Links ]
(Recibido el 15 de Julio de 2009. Aceptado el 9 de marzo de 2010)
*Autor de correspondencia: teléfono/fax: + 57 + 7 + 634 40 00, ext. 2366, correo electrónico: crcorrea@uis.edu.co (R. Correa).