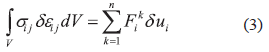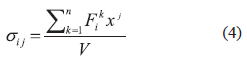Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230versão On-line ISSN 2422-2844
Rev.fac.ing.univ. Antioquia n.54 Medellín jul./set. 2010
Simulación computacional de compuestos fibrosos de baja densidad
Computational simulation of low-density fibrous composites
Fernando Ramírez1*, Paul Heyliger2, Guillermo Ramirez3, Juan Tamasco1
1 Universidad de Los Andes, Carrera 1 Este N.° 19A - 40, Bogotá- Colombia
2 Colorado State University, Fort Collins, CO 80523, USA.
3 Tennessee Technological University, Cookeville, TN 38501, USA.
Resumen
Los compuestos fibrosos de baja densidad están constituidos por fibras, adhesivo y aire, y poseen propiedades mecánicas efectivas que dependen de las propiedades geométricas y mecánicas individuales de sus constituyentes. Modelos geométricos tridimensionales de este tipo de compuestos fueron desarrollados para la evaluación computacional de sus propiedades efectivas, rigidez y resistencia. Las predicciones teóricas del modelo propuesto fueron comparadas con valores medidos experimentalmente, para un compuesto de fibras de vidrio, obteniéndose excelentes resultados. Se realizaron simulaciones de Monte Carlo para estudiar la influencia del diámetro, longitud, orientación, y propiedades mecánicas de las fibras en las propiedades efectivas del compuesto. Los resultados obtenidos indican que el parámetro más importante para la rigidez efectiva de este tipo de compuestos es la orientación de las fibras, llegando a ser el factor determinante de estas propiedades equivalentes para ciertas orientaciones.
Palabras clave: Compuestos fibrosos, simulación de Monte Carlo, propiedades efectivas
Abstract
Low-density fibrous composites are composed of fibers, binder, and air, and exhibit mechanical properties that strongly depend upon the characteristics of the individual constituents. Three dimensional models are developed to predict the effective stiffness and strength of this type of composites. The predicted computational mechanical properties are compared to experimental values obtained for a glass-fiber composite with excellent agreement. Monte Carlo simulations were then performed to study the dependence of the composite effective stiffness on fiber diameter, length, orientation and mechanical properties. Results indicate that for a specific type of fiber and volume fraction, fiber orientation is the parameter determining the behavior of the composite effective stiffness.
Keywords: Fibrous composites, Monte Carlo simulation, effective properties
Introducción
Existen numerosos estudios dedicados a la predicción de las propiedades mecánicas efectivas de compuestos fibrosos. Estos estudios presentan grandes diferencias tanto en los modelos analíticos usados como en los resultados obtenidos. Uno de los primeros estudios sobre compuestos fibrosos fue publicado por Cox en 1952 [1]. En este trabajo, Cox presentó expresiones esfuerzo- deformación de redes planas de fibras homogéneas con rigidez únicamente en tensión y compresión. Posteriormente, Astrom y Niskanen [2], desarrollaron modelos analíticos, en donde estudiaron redes de fibras con orientación y distribución espacial uniforme. En estos modelos se consideraron fibras rectas con uniones rígidas. Los autores reportaron que a bajas densidades el módulo de elasticidad varía linealmente con la densidad de la red, mientras que a altas densidades es cercano al campo homogéneo propuesto por Cox. Page y Seth [3] y Wang, Berhan, y Sastry [4] entre otros, estudiaron la influencia de los nudos en las propiedades efectivas del compuesto, mientras que diferentes modelos analíticos han sido propuestos por Arbabi y Sahimi [5], Hamlen [6], y Stahl y Cramer [7]. Más recientemente, las resistencias y rigideces efectivas de compuestos fibrosos de baja densidad fueron presentados por Hermann et al. [8], Heyden y Gustafsson [9], y Sartry, Cheng, y Wang [10]. La mayoría de estos estudios destacan las limitaciones de los modelos propuestos, y resaltan las grandes diferencias encontradas entre los valores teóricos calculados y aquellos obtenidos experimentalmente. Heyden [11] realizó un estudio detallado y propuso modelos en dos y tres dimensiones para redes de fibras de celulosa. En este trabajo los compuestos fibrosos se modelaron como conjuntos de fibras con diferentes longitudes, curvaturas, áreas de la sección transversal, rigideces y resistencias, unidas mediante nudos deformables (resortes elásticos).
El objetivo del presente estudio es la evaluación computacional de la rigidez y resistencia mecánica equivalentes de compuestos fibrosos de baja densidad. Además, mediante simulaciones de Monte Carlo determinar los parámetros con mayor influencia en las propiedades efectivas del compuesto con miras a la optimización mecánica y económica del mismo. El compuesto fibroso considerado en este trabajo está constituido por fibras de vidrio, un adhesivo que garantiza la unión de las fibras en los puntos de cruce, y aire, y cuya microestructura típica es ilustrada en la figura 1a. Este compuesto específico tiene varias aplicaciones siendo las más comunes su uso como refuerzo de tejas tipo shingle y como aislantes acústicos y térmicos. Este trabajo requiere de tres etapas. La primera es el desarrollo de un método computacional el cual incluye la generación de un modelo analítico, un procedimiento para la evaluación de las propiedades efectivas del compuesto, y la generación de un modelo geométrico. La segunda etapa es la validación del modelo propuesto mediante comparación con valores experimentales. La última etapa consiste en la generación de modelos del compuesto cuyos constituyentes posean propiedades seleccionadas de acuerdo a un análisis de Monte Carlo con el fin de determinar su influencia en las propiedades efectivas y la potencial optimización mecánica y económica del compuesto.
Figura 1 Compuestos fibrosos de baja densidad - a. Microestructura típica b. Zona típica de falla nodal
Modelo computacional
El modelo computacional usado en este estudio para la evaluación de las propiedades efectivas del compuesto fue desarrollado por los autores [12] y es presentado a continuación con el fin de generar un documento completo.
Modelo analítico
Los elementos que constituyen los compuestos fibrosos de baja densidad son las fibras que representan los elementos estructurales, y el adhesivo que forma los nudos en los puntos de contacto entre fibras. Con base en lo anterior, los compuestos fibrosos son modelados como un conjunto de elementos unidimensionales tipo viga con rigidez axial, a flexión, y a torsión. La evidencia experimental indica que las uniones entre fibras formadas por el adhesivo se rompen a niveles de deformación muy bajos, y por lo tanto son considerados en este estudio como nudos rígidos. Los elementos tipo viga en 3D tienen seis grados de libertad por nudo, y las ecuaciones que relacionan las fuerzas y desplazamientos en estos nudos están dadas por la ecuación 1.
Donde [k] es la matriz de rigidez del elemento, y {u} y {f} son los vectores de desplazamientos y fuerzas nodales respectivamente. Los componentes de la matriz de rigidez de un elemento tipo viga, arbitrariamente orientado en el espacio, pueden ser obtenidos fácilmente mediante la aplicación del principio del trabajo virtual, y son función del módulo de elasticidad, del módulo de cortante, el área y geometría de la sección transversal, y la longitud del elemento. Las matrices de los elemento son luego transformadas del sistema de coordenadas local al global, y son combinadas mediante la imposición del equilibrio de fuerzas y compatibilidad de desplazamientos en los nudos para obtener las ecuaciones globales de equilibrio del compuesto.
Propiedades efectivas
Rigidez efectiva
El objetivo de esta etapa es la evaluación de las propiedades mecánicas del compuesto para simular efectivamente un material continuo. Es decir, el volumen de control que contiene la red de fibras es reemplazado por un volumen continuo equivalente con las mismas propiedades. Esto se logra definiendo primero un volumen de control alrededor de un conjunto de fibras cuyas intersecciones con las seis caras de la caja son los nudos de frontera en los cuales se calculan las fuerzas resultantes. Luego, en las caras del volumen de control se imponen diferentes desplazamientos asumiendo movimiento afín de acuerdo a la ecuación 2.
En donde ui, εij y xj. son los componentes de los desplazamientos, deformaciones unitarias, y posición respectivamente. Notación indicial es usada donde los índices repetidos indican suma. Como los esfuerzos no pueden ser calculados en cualquier punto dentro del compuesto ya que la mayor parte de este es aire, las fuerzas en los nudos de frontera son calculadas con el fin de determinar la rigidez efectiva del material asumiendo que el volumen de control es compuesto por un sólido elástico lineal. Con base en lo anterior, se formula la ecuación 3 que representa el trabajo virtual para el modelo.
Donde σij son los componentes del tensor de esfuerzos, Fki. son las fuerzas que actúan en los n nudos k de frontera en las caras del volumen de control, y δeij y δui son las variaciones de los componentes de las deformaciones unitarias y de los desplazamientos respectivamente. Asumiendo que el esfuerzo dentro del volumen de control es constante, las ecuaciones 2 y 3 son combinadas en la ecuación 4 para obtener una expresión que permite el cálculo de los esfuerzos dentro del compuesto.
Los componentes del tensor de rigidez elástico pueden ser fácilmente obtenidos sometiendo el volumen de control a diferentes estados de deformación unitaria, calculando las fuerzas resultantes en los nudos de frontera, y usando la ecuación 4 para el cálculo de los esfuerzos en el compuesto. Los componentes del tensor de rigidez Cij son evaluados usando las relaciones esfuerzo-deformación, las cuales están dadas por la ecuación 5 empleando la convencion de Voigt para las componentes del tensor de rigidez
Los elementos del tensor de rigidez se determinan columna por columna, por ejemplo, la primera columna se determina sometiendo el volumen de control a un estado de deformaciones unitario ε1<> 0, y los demás εj=0. Los componentes de la primera columna del tensor de rigidez Ci1 son calculados a partir de los esfuerzos resultantes como Ci1= σi1/ e1 Después de obtener el tensor completo, se calcula el tensor de flexibilidad Sij con el cual se determinan finalmente las constantes elásticas de ingeniería Ex, Ey, Ez, Gyz , G xz, Gxy, vxy y vxz asumiendo que el comportamiento del compuesto fibroso es efectivamente ortotrópico.
Resistencia efectiva
La falla de un compuesto fibroso de baja densidad es un mecanismo progresivo no lineal en el cual la rigidez efectiva del compuesto decrece a medida que se presentan fallas locales que pueden ocurrir en las fibras o en los nudos. El primer tipo de falla ocurre cuando los nudos son suficientemente resistentes y las fibras son las principales responsables de la transferencia de esfuerzos en el compuesto. A medida que la carga es incrementada, las fibras más rígidas toman fuerzas mayores hasta que el esfuerzo axial excede la resistencia última del material y se alcanza el estado de primera falla de fibra. En este punto la fibra no puede transferir carga dentro del compuesto y la falla local es simulada computacionalmente retirando la fibra del modelo para los siguientes incrementos de carga. El segundo tipo corresponde a la falla de los nudos, la cual es ilustrada para el material real en la Figura 1b. El desarrollo de un modelo para este tipo de falla requiere del conocimiento de la resistencia de adherencia fibra-adhesivo, del tamaño del nudo formado por el adhesivo, y de su geometría. El primer parámetro ha sido determinado de forma experimental para el compuesto específico considerado en este estudio [13], los otros dos, tamaño y geometría, presentan grandes diferencias entre nudos y sería difícil reconstruirlos de manera exacta para el análisis computacional. En este trabajo, el proceso es simplificado asumiendo que el tamaño y la geometría es la misma para todos los nudos, y por lo tanto la cantidad de adhesivo disponible es distribuida de manera uniforme en todos los nudos del compuesto. Con base en esto, se asume que en los nudos, las fibras son cubiertas con una capa de adhesivo de espesor igual al 10% de su diámetro, lo cual junto con el volumen disponible de pegante permite calcular el área de contacto fibra-adhesivo, y la resistencia del nudo puede ser calculada usando la resistencia última de adherencia determinada mediante ensayos de laboratorio. El análisis computacional para la evaluación de la resistencia efectiva del compuesto se realiza siguiendo un proceso en el cual el modelo es sometido a una deformación unitaria en una dirección específica, luego las fuerzas internas y las relaciones de esfuerzo a resistencia última para todas las fibras y nudos son calculadas. La fibra o nudo con la mayor relación es el primer elemento que presenta una falla local y es efectivamente retirado del modelo computacional para los análisis correspondientes a los siguientes incrementos de carga. El punto correspondiente a esta falla en la curva esfuerzo-deformación del compuesto es determinado mediante la reducción de la deformación unitaria aplicada y del esfuerzo calculado dividiéndolos por la máxima relación obtenida. Este proceso se repite, después de remover del modelo la fibra o nudo que falla, hasta que el sistema no sea capaz de soportar ningún incremento en la carga. La resistencia del laminado en la dirección de la deformación unitaria impuesta será el máximo esfuerzo efectivo obtenido en este proceso.
Modelo geométrico
Los compuestos fibrosos de baja densidad son tridimensionales. Sin embargo, algunos de ellos tienen un espesor que es mucho menor que las otras dos dimensiones y el compuesto toma la forma de una hoja con espesor finito. Otros compuestos de este tipo tienen dimensiones similares en las tres direcciones y deben ser modelados considerando esta realidad. Los resultados tanto computaciona- les como experimentales que se presentan en este trabajo son para compuestos que toman la forma plana. Sin embargo, es importante mencionar que el modelo propuesto tiene la capacidad de representar compuestos fibrosos tridimensionales. Uno de los pasos más importantes en el análisis de compuestos fibrosos de baja densidad es la definición de un modelo geométrico que represente de manera precisa la geometría real del compuesto. El método usado en este estudio consiste en dividir el compuesto en un número finito de láminas cuyo espesor es dos veces el diámetro de las fibras de tal manera que el espesor de los nudos sea considerado. La red bidimensional de fibras para cada lámina es creada localizando primero una fibra en un punto aleatorio dentro del área de control, y con orientación también aleatoria o de acuerdo a una función de distribución específica. Los segmentos de las fibras que quedan por fuera del área de control pueden ser cortados, o pueden ser manejados usando condiciones de borde periódicas. Los nudos son creados en los puntos de corte de la fibra con otras fibras existentes dentro del área de control en la lámina actual. Este proceso se repite hasta que la densidad de masa del compuesto fibroso sea alcanzada. El modelo geométrico final es creado mediante la laminación de capas hasta alcanzar el espesor real del compuesto, permitiendo la creación de nudos rígidos en las intersecciones de las fibras de una capa con las fibras de las capas adyacentes.
La determinación del tamaño adecuado del volumen de control es de vital importancia en la simulación computacional del comportamiento de materiales. Con este fin se modeló un área de control cuadrado de 10,0 mm de lado y con un espesor igual al del compuesto real, lo cual resultó en un sistema de ecuaciones de cerca de un millón de grados de libertad. Para reducir el tamaño del problema, varios modelos geométricos fueron creados usando desde una hasta siete capas y sus propiedades efectivas fueron evaluadas usando el modelo propuesto. Los resultados mostraron que para más de 3 capas la variación en las rigideces efectivas calculadas era muy pequeña, y por lo tanto se concluyó que el uso de tres capas era suficiente para la representación de los compuestos fibrosos considerados. Una serie adicional de simulaciones fue realizada con el fin de determinar la influencia tanto de la relación entre el tamaño del área de control y la longitud de las fibras, como del tratamiento que se le diera a los segmentos de las fibras que quedan fuera del área del control en el proceso de generación del modelo geométrico. Seis diferentes relaciones, lado de área de control a longitud de fibra, fueron consideradas variando desde 0,5 hasta 2,0. Además, estas simulaciones se realizaron considerando tanto el caso en el cual los segmentos de las fibras por fuera del área de control son cortados, como el caso de condiciones de borde periódicas. Los resultados indicaron que a medida que el tamaño del área de control es reducido hay un incremento en las rigideces efectivas, y que para casos en los cuales la longitud del lado del área de control es al menos 10% mayor que la longitud de las fibras, los cambios en rigidez y los efectos de usar condiciones de borde periódicas son despreciables. Es importante anotar que este resultado contrasta con el valor mínimo de 3, para la relacion lado de área de control a longitud de fibra, reportado por Heyden [11] para redes de fibras de celulosa. Como resultado de estos análisis, y con el fin de generar modelos que resulten en sistemas de ecuaciones de tamaño razonable, las simulaciones computacionales se realizaron con modelos geométricos formados por tres capas y con una relación de lado de área de control a longitud de fibra de 1,5.
Simulación de Monte Carlo
Las propiedades efectivas de compuestos fibrosos de baja densidad dependen tanto de las propiedades mecánicas y físicas de sus constituyentes (fibras y adhesivo), como de la longitud, diámetro, y orientación de las fibras. Con el fin de estudiar la influencia de estos parámetros, y el potencial desarrollo de una herramienta de diseño para este tipo de compuestos, se realizó un análisis de Monte Carlo para la generación de 15.000 diferentes modelos geométricos del compuesto mediante la selección probabilística de los parámetros básicos de acuerdo a ciertas funciones de distribución. Las variables seleccionadas siguiendo el análisis de Monte Carlo para la generación de los modelos geométricos son la longitud, diámetro y orientación de las fibras, y la densidad del compuesto fibroso. Estas variables se modelaron como aleatorias con distribución uniforme en los intervalos: 3,5 a 6,5 mm, 0,012 a 0,020 mm, 0 a π, 8,5 x 10-5 a 12,5 x 10-5 g/mm3 para la longitud, diámetro, orientación, y densidad respectivamente. Con el fin de evitar que todas las fibras de un modelo específico tuvieran la misma dirección, el ángulo de orientación de las fibras fue seleccionado de acuerdo a la ecuación 6.
Donde θf es el ángulo de orientación de las fibras, θ es el ángulo seleccionado aleatoriamente, y θσ es la desviación estándar del ángulo en cada fibra del modelo. Esta desviación estándar también fue considerada como una variable aleatoria uniformemente distribuida en el rango ±π/36. Los parámetros restantes necesarios para la generación de los modelos geométricos fueron considerados como constantes. Los valores de estos parámetros son 75,0 GPa y 2,63x10-3 g/mm3 para el módulo de elasticidad y la densidad de las fibras de vidrio, una longitud del lado del área de control de 10,0 mm, y una fracción por peso de las fibras en el compuesto de 0,805. A continuación se presentan los resultados de las simulaciones de los 15.000 modelos generados, a partir de los cuales se calcularon las propiedades efectivas de los compuestos fibrosos correspondientes.
Análisis y discusión de resultados
Validación experimental
Ensayos uniaxiales de tensión de los compuestos fibrosos de baja densidad planares fueron realizados por los fabricantes del compuesto con el fin de determinar el módulo de elasticidad y la resistencia última. Una hoja típica de este compuesto tiene dimensiones de 254,0 x 254,0 x 0,889 mm y una densidad de 10,48 x 10-5 g/mm3. El módulo de elasticidad y resistencia última de las fibras de vidrio son 75,0 GPa y 3,0 GPa respectivamente. La longitud de las fibras es de 25,4 mm y su diámetro de 0,016 mm. Durante el proceso de manufactura no hay una dirección preferida para las fibras, y puede considerarse que su orientación es aleatoria. Las densidad de las fibras es de 2,63 x 10-4 g/mm3 y la del adhesivo es de 15,0 x 10-4 g/ mm3. De estos ensayos se determinó que el compuesto fibroso así fabricado tiene un módulo de elasticidad efectivo de 788,0 MPa y una resistencia ultima en tensión de 9,2 MPa. La resistencia última de adherencia entre el pegante y la fibra fue determinado también experimentalmente [13] reportando un valor de 14,4 MPa.
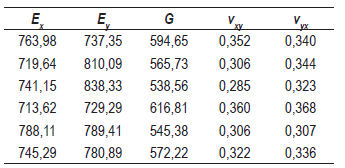
Con el fin de verificar la capacidad del modelo propuesto para predecir las propiedades efectivas de compuestos fibrosos de baja densidad cinco diferentes modelos geométricos fueron generados aleatoriamente de acuerdo a las propiedades del material real descritas en el párrafo anterior. Los resultados de rigidez obtenidos se listan en la tabla 1 en términos de módulos de elasticidad, cortante y Poisson. El valor promedio de los módulos de elasticidad calculados difiere en un 8% de los valores experimentales. Adicionalmente, las diferencias entre los valores de módulos de elasticidad y de los módulos de Poisson en direcciones perpendiculares es de sólo 5%, lo cual es un excelente indicador del comportamiento isotrópico esperado del material real considerando que la orientación de las fibras es aleatoria. Para el caso de la resistencia axial a tensión nuestro modelo predice una resistencia última de 8,7 MPa que es 5% menor que el valor medido experimentalmente. Considerando las simplificaciones de nuestro modelo con respecto al material real los resultados obtenidos con el modelo propuesto son excelentes.
Tabla 1 Propiedades elásticas efectivas. (E y G en GPa)
Estudios paramétricos - Simulación de
Monte Carlo
Módulo de elasticidad
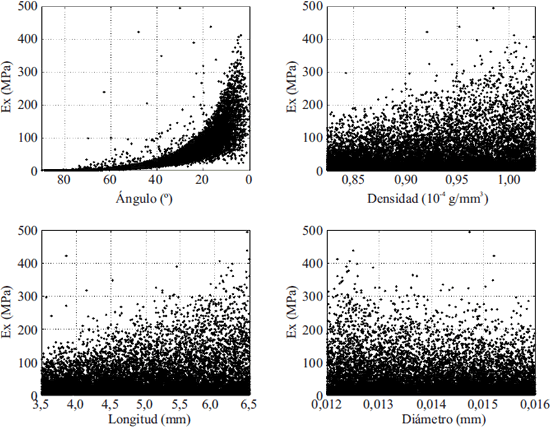
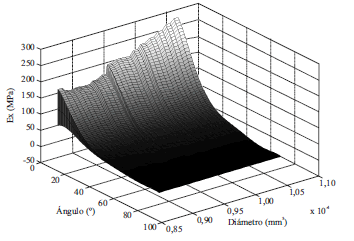
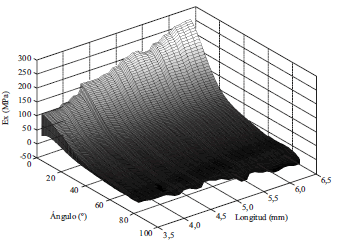
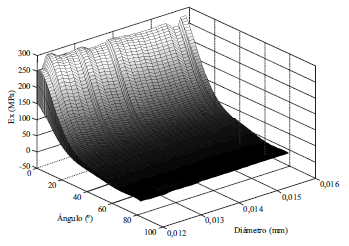
Los valores obtenidos del módulo de elasticidad para los rangos considerados de orientación, longitud y diámetro de las fibras, y de la densidad del compuesto son ilustrados en la figura 2. La orientación de las fibras tiene un clara influencia en el módulo de elasticidad. Para ángulos mayores a π/4 el módulo de elasticidad efectivo del compuesto es muy bajo, mientras que a medida que el ángulo disminuye el módulo de elasticidad aumenta, llegando a valores máximos cuando la orientación de las fibras es muy cercana a la dirección de estudio. Además, a medida que el ángulo se reduce, el módulo de elasticidad exhibe una alta variabilidad indicando que para estas orientaciones los demás parámetros considerados tienen un efecto importante. Para los casos de la variacion en la densidad del compuesto, la longitud de las fibras y el diámetro de la fibras, existe una leve tendencia del módulo de elasticidad a aumentar con el aumento de estos parámetros. Sin embargo, estos parámetros no son determinantes para el módulo de elasticidad efectivo del compuesto ya que este último muestra un gran variabilidad para los rangos de valores considerados en este estudio. Puede concluirse entonces que el parámetro con mayor influencia en el módulo de elasticidad efectivo de este tipo de compuesto es la orientación de las fibras. La dependencia del módulo de elasticidad como función de la orientación de las fibras y la densidad del compuesto, de la orientación y longitud de las fibras, y de la orientación y diámetro de las fibras es ilustrada en las figuras 3, 4 y 5, respectivamente. Para orientaciones de las fibras menores a π/4 existe un incremento en el módulo de elasticidad a medida que la densidad del compuesto, y la longitud y diámetro de las fibras aumentan. En contraste, para ángulos menores a π/4 la influencia de estos parámetros en el módulo de elasticidad es mínimo, y es la orientación de las fibras quien determina la rigidez efectiva del compuesto.
Figura 2 Variación del módulo de elasticidad (E) con la orientación de las fibras, densidad del compuesto, longitud de las fibras, y diámetro de las fibras
Figura 3 Variación del módulo de elasticidad (E) con la orientación y densidad del las fibras
Figura 4 Variación del módulo de elasticidad (E) con la orientación y longitud de las fibras
Figura 5 Variación del módulo de elasticidad (E) con la orientación y diámetro de las fibras
Módulo de cortante
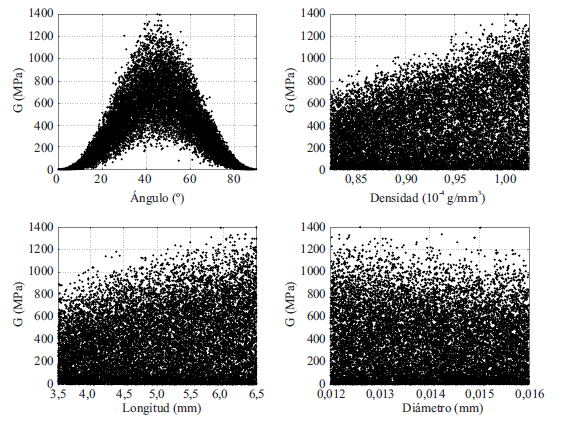
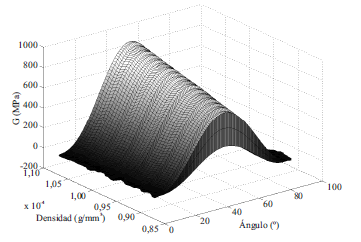
La figura 6 ilustra los valores del módulo de rigidez a cortante obtenidos a partir de las 15.000 simulaciones para los rangos considerados de orientación, longitud y diámetro de las fibras, y densidad del compuesto. De igual manera que para el módulo de elasticidad, la orientación de las fibras tiene un clara influencia en el módulo de cortante. Para orientaciones cercanas a π/4, el módulo de cortante alcanza un valor máximo, y este se reduce a medida que el ángulo de las fibras se aleja de este ángulo, alcanzando un valor mínimo cuando las fibras son paralelas o perpendiculares a los lados del volumen de control. La variabilidad que exhibe el módulo de cortante para los rangos de densidad del compuesto, y longitud y diámetro de las fibras considerados, indican que el efecto individual de estos parámetros no es determinante para la rigidez efectiva del compuesto. Las figuras 7, 8, y 9 ilustran al variación del módulo de cortante con la orientación de las fibras para diferentes densidades del compuesto, longitudes y diámetros de fibras, respectivamente. Para ángulos cercanos a π/4 existe un tendencia de la rigidez a cortante a aumentar con el aumento en los demás parámetros, mientras que para otros ángulos esta tendencia se reduce hasta que es la orientación de las fibras el parámetro que controla la rigidez efectiva del compuesto.
Figura 6 Variación del módulo de cortante (G) con la orientación de las fibras, densidad del compuesto, longitud de las fibras, y diámetro de las fibras
Figura 7 Variación del módulo de cortante (G) con la orientación de las fibras y densidad del compuesto
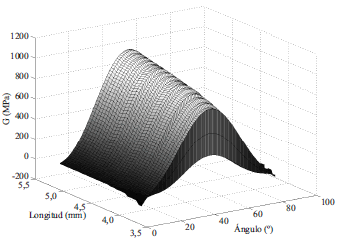
Figura 8 Variación del módulo de cortante (G) con la orientación y longitud de las fibras
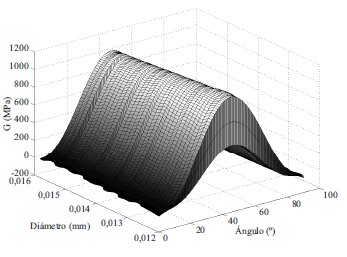
Figura 9 Variación del módulo de cortante (G) con la orientación y diámetro de las fibras
Conclusiones
En este trabajo se desarrolló y validó un modelo computacional para la evaluación de las propiedades mecánicas efectivas de compuestos fibrosos de baja densidad. La influencia de la longitud, diámetro, y orientación de las fibras, y densidad del compuesto fue estudiada mediante la simulación de 15.000 modelos generados de acuerdo a un análisis de Monte Carlo. Para los materiales y parámetros considerados en este estudio puede concluirse:
El parámetro con mayor influencia en la rigidez efectiva del compuesto es la orientación de las fibras, el módulo de elasticidad es mayor para compuestos cuyas fibras están orientadas en la dirección de la deformación aplicada, mientras que el de cortante es mayor para ángulos de π/4.
El efecto del diámetro y longitud de las fibras, y de la densidad en la rigidez de tensión y cortante del compuesto se reduce a medida que la orientación de las fibras se acerca a la dirección de esfuerzo normal o cortante aplicado, respectivamente.
Para una densidad y orientación de las fibras dadas, el diámetro no tiene un efecto significativo en las propiedades efectivas, mientras que el aumento en la longitud de las fibras resulta en un aumento de estas propiedades, siendo este efecto mayor para las orientaciones que maximizan las propiedades mecánicas respectivas. El modelo propuesto y las simulaciones realizadas permitirán el estudio de la influencia de los defectos en insumos y de manufactura en las propiedades del compuesto, el estudio de la falla progresiva, y el desarrollo de herramientas de diseño para este tipo de compuestos.
Referencias
1. H. L. Cox. "The Elasticity and Strength of Paper and Other Fibrous Materials". Journal of Appl.edPhys.cs. Vol. 3. 1952. pp. 72-79. [ Links ]
2. J. A. Astrom, K. J. Niskanen. "Simulation of network fracture". Proceedmgs of the 1991 International Paper Phys.cs Conference. Ed. TAPPI. Atlanta (GA). 1991. pp. 31-47. [ Links ]
3. D. H. Page, R. Seth. "The Elastic Modulus of Paper II. The Importance of Fiber Modulus, Bonding, and Fiber Length". TAPPIJournal. Vol. 63. 1980. pp.113-116. [ Links ]
4. C. W. Wang, L. Berhan, A. M. Sastry. "Structure, Mechanics and Failure of Stochastic Fibrous Networks: PartI - Microscale Considerations". Journal of Engineering Materials and Technology. Vol. 122. 2000. pp. 450-459. [ Links ]
5. S. Arbabi, M. Sahimi. "Elastic Properties of Three Dimensional Percolation Networks with Stretching and Bond-Bending Forces". Physical Review B. Vol. 38. 1988. pp. 7173-7176. [ Links ]
6. R. C. Hamlen. Paper Structures, Mechanics, and Permeability. Computer Aided Modeling. PhD. Thesis. University of Minessota. Minneapolis, Minessota. 1991. pp. 122-128. [ Links ]
7. D. C. Stahl, S. M. Cramer. "A Three Dimesional Network Model for a Low Density Fibrous Compose". Journal of Engineering Materials and Technology. Vol. 120. 1998. pp. 126-130. [ Links ]
8. H. J. Herrmann, A. Hanson, S. Roux. "Fracture of Disordered, Elastic Latices in Two Dimensions". Physical Review B. Vol. 39. 1989. pp. 637-648. [ Links ]
9. S. Heyden, P. J. Gustafsson. "Simulation of Fracture in a Cellulose Fiber Network". Journal of Pulp and Paper Science. Vol. 24. 1998. pp. 160-165. [ Links ]
10. A. M. Sastry, X. Cheng, W. Wang. "Mechanics of Stochastic Fibrous Networks". Journal of Thermoplastic Composite Materials. Vol. 11. 1998. pp. 288-295. [ Links ]
11. S. Heyden. Network Modelling for the evaluation of Mechanical Properties of Cellulose Fiber Fluff. PhD. Thesis. Lund University, Division of Structural Mechanics. Lund. Sweden. 2000. pp. 177-180. [ Links ]
12. F. Ramirez, P. Heyliger. "Effective Mechanical Properties of Low Density Fiber Composites". International Journal for Computational Methods in Engineering Science and Mechanics. Vol. 9. 2008. pp. 91-102. [ Links ]
13. L. T. Drzal, E. K. Drown. Johns-Manville Fiber/Binder Adhesion Measurements. Test Report. Michigan State University. USA. 2002. pp. 2-4. [ Links ]
(Recibido el 27 de agosto de 2009. Aceptado el 12 de abril de 2010)
*Autor de correspondencia: teléfono: + 57 + 1 + 339 49 49 ext. 2854, fax: + 57 + 1 + 332 43 13, correo electrónico: framirez@uniandes.edu.co (F. Ramírez)