Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.55 Medellín Sept. 2010
Optimización de diseño de llantas de aluminio a flexión mediante el método de elementos finitos
Design optimization of aluminum rims in bending by finite element analysis
Fabio Marcelo Peña Bustos
Universidad Autónoma de Manizales. Facultad de Ingeniería Grupo de Investigación en Diseño Mecánico y Desarrollo Industrial ''Arquitas''. A. A. 441. Manizales, Caldas, Colombia.
Resumen
El presente trabajo da a conocer el proceso llevado a cabo para la optimización del diseño estructural a fatiga por flexión de llantas de aluminio automotrices en una empresa ubicada en la ciudad de Manizales, Colombia. El proceso se efectuó relacionando los análisis de elementos finitos con los resultados de la prueba física de fatiga por flexión, demostrando que el diseño de llantas de aluminio puede optimizarse reduciendo el tiempo de desarrollo de cada modelo, obteniendo llantas más livianas, lo cual significa ahorro en costos de desarrollo y manufactura del producto con las consecuentes mejoras de eficiencia y desempeño de los vehículos. Además, la incorporación temprana de la simulación el proceso de desarrollo del producto da como resultado diseños que pueden optimizarse antes de fabricar y ensayar los prototipos físicos.
El trabajo presentado da a conocer entonces, cómo se ha incorporado exitosamente el análisis de elementos finitos como parte del proceso normal de diseño de llantas de la empresa objeto de estudio, con los consecuentes beneficios en términos de confiabilidad y productividad.
Palabras clave: Análisis de elementos finitos FEA, fatiga a flexión, llantas de aluminio
Abstract
This paper shows the process for optimization of structural design to fatigue bending aluminum wheels in a company located in the city of Manizales, Colombia. The process was conducted relating the finite element analysis with fatigue bending tests results, demonstrating that the design of aluminum wheels can be optimized by reducing the development time of each model, getting lighter wheels, which means savings cost of development and manufacturing of the product with consequent improvements in efficiency and performance of vehicles. Furthermore, if the simulation is performed early in the product development process, designs can be optimized prior to manufacture and testing of physical prototypes. The work presented shows how the finite element analysis has successfully incorporated as part of the wheels normal design process in the company, with consequent benefits in terms of reliability and productivity.
Keywords: Finite element analysis, bending fatigue, aluminum rims
Introducción
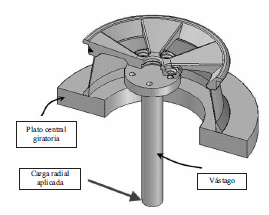
En la fabricación de llantas de aluminio, se emplean tres pruebas para evaluar el comportamiento estructural de la llanta: la prueba de fatiga a flexión, la prueba de fatiga radial y una prueba de impacto. Cada diseño particular, debe satisfacer condiciones especificadas por norma para cada una de estas pruebas. La prueba que históricamente ha demostrado ser más severa es la de fatiga por flexión [1]. El esquema de la prueba de fatiga por flexión se muestra en la figura 1 .
Figura 1 Esquema del montaje de la prueba de fatiga a flexión
La pestaña inferior de la llanta se fija solidariamente a un plato giratorio a la vez que se adhiere, mediante los pernos de fijación del cubo central a un vástago al que se aplica una carga radial de di-rección fija. El estado de flexión inducido sobre la llanta produce fluctuaciones del esfuerzo en cada punto a medida que la llanta gira sobre su eje durante la prueba. Estas fluctuaciones del esfuerzo dan lugar a agrietamientos por fatiga después de un número determinado de ciclos. Dependiendo de la aplicación del modelo de llanta particular, las normas exigen una intensidad de carga y un número determinado de ciclos sin que se presente agrietamiento, usualmente evidenciado mediante la técnica de tintas penetrantes.
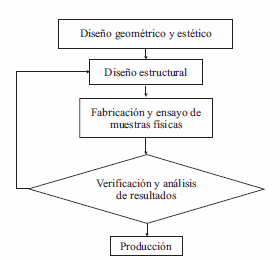
En el proceso de diseño estructural de la llanta, es necesario ajustar la geometría del sólido a fin de alcanzar las especificaciones particulares. Esto usualmente implica un costoso procedimiento de prueba y error mediante la fabricación y ensayo de varios tirajes de prototipos físicos, hasta lograr que la llanta satisfaga los requerimientos. El procedimiento tradicional de diseño se muestra en la figura 2 .
El informe del proyecto europeo CAROW [2] indica que el proceso de diseño utilizado por los fabricantes de llantas de aluminio es todavía básicamente heurístico para cada nuevo modelo y que la conveniencia del diseño tiene que ser validada mediante procesos de certificación lentos y costosos. El mismo informe señala que cada caso de molde inapropiado cuesta unos 30.000 € y retarda el proceso entre 6 y 14 semanas dependiendo de la complejidad del modelo. Hsu [1] informa que, sin la ayuda de simulaciones computaciona- les cuidadosas, se requieren de 3 a 4 tirajes con reformas o re-manufactura del molde para un nuevo diseño de llanta hasta que este finalmente pasa las pruebas físicas.
Figura 2 Esquema del proceso tradicional de diseño de llantas de aluminio
El proceso de diseño de llantas de aluminio puede optimizarse [2] mediante la introducción de técnicas numéricas de simulación en las etapas tempranas del diseño y desarrollo del producto y antes de cualquier producción. De esta manera puede hacerse que el sólido alcance las especificaciones de fatiga por flexión, con un mínimo de iteraciones, reduciendo el peso de la llanta. Los objetivos principales del rediseño geométrico son la reducción de esfuerzos y peso.
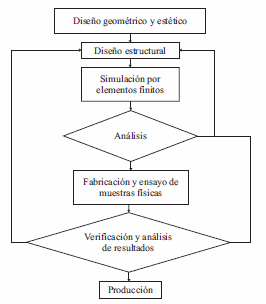
La figura 3 muestra el procedimiento de diseño sugerido incluyendo la simulación por elementos finitos. Además de las especificaciones de la prueba de flexión, el diseño estructural está sometido a una serie de restricciones geométricas y de proceso, que deben tenerse en cuenta al momento de proponer las reformas del sólido.
Análisis de elementos finitos
Geometría CAD vs. Enmallado
Para efectuar los análisis de elementos finitos se utilizó el programa ANSYS 8.0®. Debido a la complejidad de la geometría del sólido de la llanta, una de las principales dificultades consiste en la introducción de la geometría dentro del programa de elementos finitos para el enmallado.
Figura 3 Esquema del proceso de diseño de llantas de aluminio incluyendo el análisis por elementos finitos
Beall et al. [3] reconocen que actualmente uno de los principales obstáculos para incorporar las simulaciones como un ingrediente esencial del proceso de diseño es la introducción de la geometría dentro del programa de elementos finitos con fines de enmallado. Rhoades [4] informa que en ciertas industrias hasta el 70% de las horas hombre invertidas en el análisis de elementos finitos y procesos de simulación se consumen en el re-trabajo o la re-creación de los modelos CAD antes que se pueda comenzar el análisis.
Usualmente, las incompatibilidades geométricas generadas por la traslación entre sistemas CAD resultan en una geometría ''sucia'' difícil de enmallar. Los archivos CAD contienen rasgos que son difíciles de enmallar, tales como áreas alargadas, ''grietas'', huecos, traslapes y malcondicionamientos de tangencias, así como otras inconsistencias geométricas. La ayuda del programa ANSYS [5] señalan varias causas para la falla de la importación del sólido.
Es interesante que Beall [3] señale que parte de la complej idad asociada con acceder a la geometría del sólido para el enmallado se debe atribuir al hecho de que históricamente, los análisis de elementos finitos se introducen muy tarde en el proceso de diseño y el modelo CAD contiene más detalles de los que son apropiados para el análisis. En el caso específico de las llantas de aluminio, el hecho de que el diseño estético anteceda y prevalezca inicialmente sobre el estructural, introduce gran parte de las complicaciones que se han señalado. Se sugieren diversas estrategias en [3-5] para tratar con los problemas geométricos para el enmallado.
Comportamiento del material
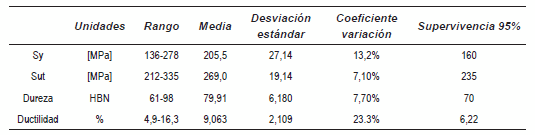
La tabla 1 muestra el resumen estadístico de las propiedades de la aleación de aluminio y silicio al 7%, utilizada para la fabricación de llantas basada en la tabulación de 250 pruebas de tracción simple y otros ensayos de laboratorio. En la tabla 1 la resistencia a la fluencia del material se nota como Sy y la resistencia última como Sut. Los valores de la última columna, confiabilidad de supervivencia Weibull de 3 parámetros, fueron utilizados como datos de comparación en los modelos. La suposición de elasticidad lineal es adecuada por ser una aplicación de fatiga de altos ciclos [6], donde la resistencia a la fatiga a la duración requerida es muy inferior al límite elástico del material [7].
Tabla 1 Resumen de los estadísticos de las propiedades mecánicas de la aleación de aluminio Al Si 7%, a partir de 250 pruebas de laboratorio
Dirección variable de la carga
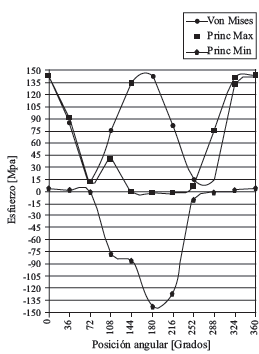
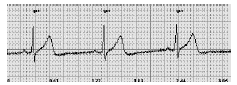
Este trabajo demostró que la variación de la posición angular de la carga induce patrones de esfuerzo en los puntos críticos que pueden considerarse prácticamente alternantes, como se muestra en la figura 4 .
Condiciones de frontera
Los análisis preliminares de elementos finitos mostraron que mediante restricciones simplificadas, e inversión de la carga es posible encontrar los puntos críticos que presentan agrietamiento en las pruebas, siempre que estos estén alejados de la zona de pernos, según se ilustra en la figura 5 .
Modelos con gruesas simplificaciones en las condiciones de apoyo y en la forma de aplicación de la carga brindan información de carácter cualitativo respecto a la ubicación de los puntos de máximo esfuerzo de los radios. Sin embargo, la forma de aplicación de la carga en el modelo afecta significativamente la magnitud de los esfuerzos en las zonas críticas, debido a la diferencia en el patrón de desplazamientos impuesto sobre la llanta.
Para obtener información precisa sobre la intensidad de los esfuerzos en la prueba, deben ajustarse las condiciones de frontera y la forma de aplicación de la carga, de manera que emulen de manera más precisa el patrón de desplazamientos impuesto en la prueba de flexión. Adicionalmente, para obtener información confiable sobre el estado de esfuerzos en la zona central del llanta, el modelo debe contemplar el efecto del apriete de pernos y su interacción con la carga de flexión.
Figura 4 Variación de los esfuerzos equivalentes de Von Mises, principal máximo y mínimo con la posición angular, en uno de los puntos críticos de una llanta Mazda en la prueba de flexión
Figura 5 Modelos simplificados muestran la ubicación de los puntos críticos (izquierda), que coinciden con los agrietamientos que se presentan en la prueba física (derecha). Esfuerzo indicado en MPa
Influencia del apriete del perno en el estado de esfuerzos
Para hacer más preciso el modelo en la zona del cubo fue necesario tomar en consideración el estado de esfuerzos inducido por el apriete de pernos y la forma como se transfiere la carga desde el vástago central hasta la zona de apoyo. Esto implicó la utilización de elementos de malla especializados para simular el apriete así como contemplar las no linealidades debidas al contacto con fricción entre el llanta y la rígida base giratoria de acero. La figura 6 muestra el patrón de esfuerzos principales compresivos inducidos por el perno con asiento cónico. Este patrón de esfuerzos determina la distribución de presiones de contacto entre la llanta y la rígida base de acero y permite evaluar de forma más precisa el estado de esfuerzos en la zona central de la llanta. La precarga en los pernos puede simularse de una forma flexible y eficaz como una carga interna al modelo mediante la utilización de elementos PRETS179.
Figura 6 Patrón de esfuerzos principales compresivos inducidos por el apriete del perno con asiento cónico
Cuando se introducen las no linealidades debidas al contacto con fricción entre piezas, se presentan dificultades en la convergencia del modelo. La convergencia de un modelo que contemple simultáneamente el apriete de pernos, las condiciones no lineales de contacto y la carga de flexión se puede mejorar enormemente mediante la aplicación independiente y gradual de la carga en sub-etapas y el uso de resortes débiles. La figura 7 muestra el conjunto utilizado para el análisis de elementos finitos de la prueba de flexión, con la carga en una de las posiciones críticas. Este modelo contempla la alta rigidez de la base giratoria, el contacto con fricción entre llanta y base, así como apriete de pernos. El patrón de desplazamientos inducido por este estado de carga se muestra en la figura 8 y es mucho más cercano al impuesto durante la prueba de flexión que los modelos preliminares con grandes simplificaciones descritos anteriormente. La figura 9 muestra cómo las condiciones del modelo ya mencionadas, permiten obtener información cuantitativa más confiable sobre el estado de esfuerzo en la zona central de la llanta. Ilustra los puntos críticos sometidos a esfuerzos elevados, que condujeron a agrietamiento en la prueba física.
Figura 7 Conjunto CAD utilizado para el análisis de elementos finitos de la prueba de fatiga por flexión mostrando la carga en una de las posiciones críticas
Optimización del diseño geométrico
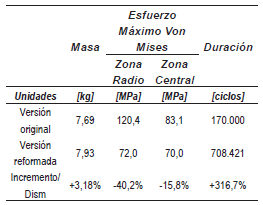
Como se ha señalado, las reformas geométricas tendientes a reducir el esfuerzo se llevan a cabo sobre una base heurística y típicamente resultan en un aumento de la masa de la llanta. A manera de ejemplo, la tabla 2 muestra el efecto de las reformas realizadas en una llanta Mazda de 16 pulgadas, y señala las diferencias entre la versión original y la versión reformada, sobre una base heurística, que pasó la prueba de flexión y fue aprobada para fabricación. Los esfuerzos indicados en la tabla se encontraron utilizando las condiciones del modelo descritas arriba, incluyendo el efecto del apriete de pernos.
Figura 8 Patrón de desplazamientos inducido en la prueba de flexión para una de las posiciones críticas, encontrado mediante un modelo que contempla el apriete de pernos y la rigidez del plato giratorio
Figura 9 Patrón de esfuerzos equivalentes de von Mises en la zona central del cubo (izquierda). Se indican los puntos de máximo esfuerzo, que coinciden con los puntos donde se presentó agrietamiento en la prueba física (derecha)
Modelos simplificados basados en parámetros
En el presente trabajo se mostró cómo la reducción de esfuerzos y peso pueden buscarse ágilmente de forma simultánea mediante modelos CAD simplificados del sólido de la llanta basados en parámetros. El estado de carga de los radios en una de las posiciones críticas puede asimilarse a una viga en voladizo con una fuerza en el extremo.
Tabla 2 Efecto de las reformas realizadas en una llanta Mazda de 16 pulgadas, sobre una base heurística, según el procedimiento tradicional de diseño
Un modelo simplificado de un solo radio del llanta en este estado de carga conduce a los mismos puntos críticos que en un modelo de llanta completo y tiene la ventaja de dar resultados precisos aún con una base de datos reducida, dando lugar a tiempos bajos de resolución, importantes durante la fase de exploración de rediseño donde es clave conocer rápidamente el impacto de los cambios en los parámetros geométricos sobre la intensidad máxima de los esfuerzos en los puntos críticos.
Mediante diferentes técnicas como análisis de rigidez de la sección, optimización topológica y otras, es posible distinguir qué parámetros geométricos tienen un impacto significativo en la reducción de esfuerzos. En el proceso de diseño, una vez definidos los parámetros relevantes, es posible generar un diseño de experimentos con la ayuda de Ansys Designxplorer® a fin de encontrar una curva de respuesta que permita establecer la dependencia entre los parámetros elegidos y las intensidades de esfuerzo en los puntos críticos. Sobre la curva de respuesta puede elegirse un juego de parámetros que cumpla con alguna meta predeterminada de reducción de esfuerzos o peso durante el diseño. Una vez elegidas las combinaciones de parámetros que conducen las metas de diseño, pueden realizarse las verificaciones de los sólidos resultantes con modelos de llanta completa.
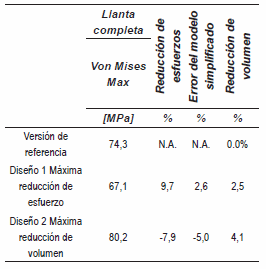
La tabla 3 muestra que los modelos simplificados dan cuenta de la variación de los esfuerzos en los modelos de llanta completa con una precisión del 5% para una llanta Mazda de 16 pulgadas. En la primera columna se dan las intensidades de esfuerzos equivalentes de Von Mises en los puntos críticos en MPa y se notan como VM Max.
Tabla 3 Comparación entre la reducción de esfuerzo y de volumen lograda con el modelo simplificado y con un modelo de llanta completo para dos juegos de parámetros, en una llanta Mazda de 16 pulgadas
Conclusiones
Se investigaron las condiciones del modelo de elementos finitos que permiten encontrar los puntos críticos de esfuerzo tanto en la zona de los radios como en la parte central de la llanta, para la prueba de fatiga por flexión y se verificaron mediante pruebas físicas. La incorporación del análisis de elementos finitos en el proceso de diseño presenta las siguientes ventajas:
- La respuesta de la llanta a las cargas de flexión se conoce antes de que se haya fabricado el molde y el primer tiraje.
- Se dispone de un medio para cuantificar el impacto de las modificaciones geométricas propuestas en el estado de esfuerzos de la llanta.
- Al conocer el impacto de las reformas geométricas del sólido sobre el estado de esfuerzos, es posible reducir el número de tirajes y pruebas físicas hasta alcanzar un diseño que satisfaga la duración requerida en la prueba de flexión.
- Se pueden controlar los casos en los que las reformas geométricas cambian la ubicación de los esfuerzos máximos pues se dispone del estado de esfuerzos después de la modificación y puede determinarse la influencia de los parámetros geométricos en la ubicación e intensidad de los esfuerzos máximos.
- Las reformas de diseño tendientes a la reducción de peso se facilitan pues se puede medir su impacto en la intensidad de los esfuerzos. Si bien los dos criterios pueden estar en conflicto, se puede hallar la reducción máxima tolerable de peso manteniendo un nivel admisible de esfuerzo.
Adicionalmente, se propuso una metodología detallada de diseño para efectuar las reformas geomé-tricas tendientes a que la llanta pase la prueba de flexión, incorporando el análisis de elementos finitos y contemplando de forma simultánea los criterios de reducción de esfuerzos y peso. Se elaboró una curva esfuerzo vida para 9 modelos de llantas de una misma aleación de aluminio a partir de los análisis de elementos finitos y de los resultados de 46 pruebas físicas de flexión rotativa. La figura 10 muestra estos datos en dispersión y es una gran ayuda para el proceso de diseño pues representa la respuesta del producto en la prueba física e incorpora la variabilidad debida a los numerosos factores del proceso de manufactura en la respuesta a la fatiga.
Los resultados del presente estudio están siendo aplicados por el fabricante en el desarrollo de diversos modelos de llantas a fin de mejorar su desempeño en la prueba de flexión y disminuir su peso. Se aplicó el procedimiento descrito a un esbelto llanta Mazda de 16 pulgadas obteniendo una reducción de peso de 2% respecto al modelo actual, manteniendo los niveles de esfuerzo y por lo tanto la duración en la prueba. Este ahorro representa unas 200 unidades adicionales por semestre utilizando la misma cantidad de material, para el volumen actual de producción.
Figura 10 Datos de esfuerzo-vida en dispersión para 46 pruebas físicas efectuadas sobre nueve modelos de llantas fabricados de la misma aleación de aluminio
Referencias
1. Y. Hsu, S. Wang, T. Liu. ''Prediction of fatigue failures of aluminum disc wheels using the failure probability contour based on historical test data''. ''Journal of the Chinese Institute of Industrial Engineers''. Vol. 21. 2004. pp. 551-558. [ Links ]
2. High-Performance Computing and Networking (HPCN). Public Final Report of ESPRIT HPCN PST Activity, CAROW - Cast Aluminium Road Wheels. Munchen (Germany). 1999. www.gmd.de/de/newpdl/carow.pdf. pp. 30-36. Consultada el 20 de junio de 2005. [ Links ]
3. M. W. Beall, J. Walsh, M. S. Shephard. ''Accessing CAD geometry for mesh generation''. 12th International Meshing Roundtable. 2003. New Mexico (USA). pp. 1. http://www.imr.sandia.gov/papers/imr12/beall03. pdf, Consultada el 14 de junio 2009. [ Links ]
4. G. Rhoades. Data intraoperability: upstream and downstream solutions. Ansys Solutions. Vol. 3. 2001. pp. 7-11. [ Links ]
5. Ansys Inc. Release 11 ''Documentation for ANSYS. Modeling and Meshing''. Chapter 6. Importing solid models from IGES files. Canonsburg (PA). 2007. pp. 89-110. [ Links ]
6. N. E. Dowling, Mechanical Behavior of Engineering Materials, Engineering Methods of Deformation Fatigue and Fracture. 2a ed. Ed. Prentice Hall. New Jersey. 1998. pp. 357-419. [ Links ]
7. R. Juvinall, K. Marsheck. Fundamentals of machine components design. 2a Ed. Ed. Jhon Wiley & Sons. New York. 1967. pp. 267-322. [ Links ]
(Recibido el 06 de Junio de 2009. Aceptado el 19 de abril de 2010)
1Autor de correspondencia: teléfono: + 57 + 6 + 872 72 11, fax: + 57 + 6 + 872 71 85, correo electrónico: fabiope@autonoma.edu.co. (F.M. Peña)