Analysis and convergence of weighted dimensionality reduction methods

Análisis y convergencia de métodos de reducción de dimensionalidad ponderados

Juan Carlos Riaño Rojas¹* , Flavio Augusto Prieto Ortiz.², Edgar Nelson Sánchez Camperos.³, Carlos Daniel Acosta Medina.¹, Germán Augusto Castellanos Domínguez¹

¹Universidad Nacional de Colombia Sede Manizales. A.A. 127. Km 9 vía el aeropuerto campus la Nubia Manizales, Colombia

²Universidad Nacional de Colombia Sede Bogotá. A.A. 14490. Carrera 30 N° 45-03 Edificio IEI 406 Bogotá D.C., Colombia

³Centro de Investigaciones Avanzadas IPN, Cinvestav. Guadalajara. Av. Científica 1145 , colonia el Bajío, Zapopan , 45015, Jalisco, México

---

Abstract

We propose to use a Fisher type discriminant objective function addressed to weighted principal component analysis (WPCA) and weighted regularized discriminant analysis (WRDA) for dimensionality reduction. Additionally, two different proofs for the convergence of the method are obtained. First one analytically, by using the completeness theorem, and second one algebraically, employing spectral decomposition. The objective function depends on two parameters U matrix being the rotation and D diagonal matrix weight of relevant features, respectively. These parameters are computed iteratively, in order to maximize the reduction. Relevant features were obtained by determining the eigenvector associated to the most weighted eigenvalue on the maximum value in U. Performance evaluation of the reduction methods was carried out on 70 benchmark databases. Results showed that weighted reduction methods presented the best behavior, PCA and PPCA lower than 17% while WPCA and WRDA higher than 45%. Particularly, WRDA method had the best performance in the 75% of the cases compared with the others studied here.

Keywords:PCA, PPCA, WPCA, WRDA, dimensionality reduction.

---

Resumen

En este trabajo se propone utilizar una función objetivo discriminante tipo de Fisher, para la reducción de la dimensionalidad, en el análisis de componentes principales ponderados (WPCA) y al análisis discriminante regularizado ponderados (WRDA). Además, se desarrollan dos pruebas de la convergencia del método. Primero analíticamente, usando el teorema de completitud, y una segunda prueba algebraica, empleando descomposición espectral. La función objetivo depende de dos parámetros: U matriz de rotaciones y D matriz pesos de características relevantes, respectivamente. Estos parámetros se calculan iterativamente, para maximizar la reducción. Las características relevantes fueron obtenidas determinando el vector propio asociado al valor propio con máximo valor en U. La evaluación del desempeño de los métodos de la reducción fue realizada sobre 70 bases de datos (benchmark). Los resultados mostraron que los métodos ponderados presentan un mejor comportamiento PCA y PPCA por debajo del 17% mientras que WPCA y WRDA por encima del 45%. Particularmente, el método WRDA tuvo el mejor funcionamiento en el 75% de los casos comparados con los otros estudiados en este trabajo.

Palabras clave:WPCA, WRDA, reducción de dimensión.

---

Introduction

The relevant information extraction from a data set with a great number of features has been considered as a big problem in machine learning and pattern recognition. These great sets appear normally in areas as bioinformatics and text recognition, where is common to find feature vectors with dimensions higher than 107, but with a low number of relevant characteristics. Thus, the classification algorithm performance is limited and their computing time is high, reducing the application in real time tasks [1]. For solving this problem, irrelevant features that do not contribute to the extraction and selection process must be rejected, improving the classifiers performance. Traditionally, the dimensionality reduction has been developed by using linear techniques such as principal components analysis (PCA), probabilistic principal components analysis (PPCA) and factorial analysis [2-4]. Nevertheless, these linear techniques are not suitable for handling non linear complex data. For this reason, in recent years, a great number of non linear techniques for dimensionality reduction have been proposed several geometric methods for feature selection and dimensional reduction. Where they divide the methods into projective methods and methods that model the manifold on which the data lies. For projective methods, we review projection pursuit, principal component analysis (PCA), kernel PCA, probabilistic PCA, and oriented PCA; and for the manifold methods, we review multidimensional scaling (MDS), landmark MDS, Isomap, locally linear embedding, Laplacian eigenmaps and spectral clustering [5-7]. Nevertheless they lack of convergence analysis. Non linear reduction techniques have a good performance in complex artificial tasks; however, they do not overcome the traditional linear techniques in real word tasks using several databases without carrying out formal proofs of this fact [8]. In [9] an algebraic weighted variables approximation is presented. It is based on the Kernel matrix spectral properties. The main contribution consists in obtaining relevant variables using the weighted objective function, proving its convergence on employing strong hypothesis from the analysis fundaments, but being different to those used in this paper. An exhaustive review in extraction and selection features methods classification, grouping them in two classes, has been done in [10]. The first one contains the binary search methods, which at the same time are catalogued as exhaustive search methods but forbidden because of its computational cost. These find the optimum of the objective function but provide unstable and not optimal results. The second group includes the weighted methods that multiply the features by continuous values, in order to employ mathematical analysis techniques, for optimizing the objective function. In reference [11-14] descriptive studies of the reduction and regression methods are observed. Some of them show applications in pattern classification for identifying faces, while others present applications for materials science. Although the two last references have the same abbreviation (WPCA) they refer to other aspects, employing "W" for window or whitened, being different to the methods considered in this paper, because they carried out a local reduction.

In this work, a complete study of two of these weighted methods is included, WPCA and WRDA. These methods were already introduced in [15,16] by using an EM algorithm and without including a theoretical study. The main advantage of these methods is the capability of combining in one step two tasks (features selection and extraction), returning the called relevant features. Here we present the methods as weighted rotations for maximizing the objective function J which is the matrix traces ratio that represents the inter­classes and intra-classes dispersion. From this definition, we develop a convergence analysis. The main convergence result is obtained from two different points of view. First analytically by using the completeness theorem and second algebraically, employing spectral decomposition.

The convergence was validated employing artificial and real data for selecting relevant variables from a set of 70 geometric features (areas, perimeters, fractal dimension, curvatures, Hausdorff dimension among others), statistical (correlations, means, entropy and moments) needed for characterizing patterns that can separate two classes. In order to evaluate the performance of these methods, the ROC surfaces hyper-volume (hyper-surface) has to be calculated by using the Monte Carlo method, additional to the error classification.

Methodology

Relevance and variables selection using weighting

The variables selection problem can be understood as choosing a subset of p features, from the whole features set c, that allows obtaining a suitable performance in the classification process.This kind of search is handled by some evaluation function named the relevant set. On the other hand, the extraction techniques carry out a transformation of c features space to a lower dimension space. In order to guarantee the optimum solution, these methods execute an exhaustive search, increasing the computational cost. For solving this problem, heuristic methodology has been proposed, but producing unstable behavior respect to the objective function. Other alternative consists in using weighting methods, although they are not the optimum solution, they are more stable and flexible, producing a suitable solution [17]. Some of these methods are described below.

Weighted probabilistic PCA

It is a particular factorial analysis case. In this method, the original X features are observed as a linear combination of Z factors group, joined to a specific error V and C that represent charge coefficients that are modeled according to (1):

Where the random variables Z can be assumed non dependent and identically distributed, with a unitary spherical Gaussian variance. Note that there is a difference between the probabilistic model PCA (PPCA) and PCA, where the random variable variance can be associated to the diagonal elements of Z. The model also considers the general perturbation matrix V, but in [18] a restriction of Gaussian variance R = εI (isotropic noise) is stated. The previous model formulation is modified by introducing the weights on the original variables (features) and thus containing the weighted rotation. Let D be a diagonal matrix that contains the i-th variable in the d_ii element. If the new variable is assumed as d_iix_i, a new data subset y = Dx is generated, where the probabilistic model is defined in (2):

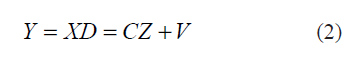
where Z and V are distributed as in equation (1). From this definition Y is normally distributed, with mean equal to zero and the covariance given by (3):

The weights are found in D and they are responsible of generating the noise for the X variables. From (3) the EM (Expectation - Maximization) algorithm is obtained, in order to estimate the unknown variables state in the E-step and maximizing the total probability from the estimation of Z and the observation of Y, in the M-step. E-step and M-step are observed in equation (4) and (5), respectively:

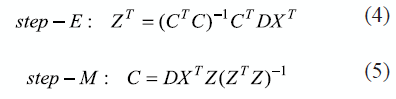
Weighted regularized discriminant Analysis WRDA

RDA was proposed by Friedman [19] for being used in small samples, where data possess high dimensionality, trying to overcome the discriminant rule degradation. In this document, they were identified as the regularized linear discriminant analysis method. The aim of this technique is to find the lineal projection space where the dispersion between classes was the maximum value. One way consists in maximizing the ratio between projected classes in the dispersion matrix inter-classes ∑_B and the dispersion matrix intra-class ∑_W, as is expressed in (6):

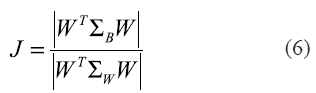
where W is the projection matrix, which dimension is defined by the number of linearly separated classes k. The aim is to maximize the previous objective function (6), under restriction |W^T∑_WW| = 1. The solution is obtained employing the Lagrange multipliers, the solutions are k-1 eigenvectors generalized from ∑_B and ∑_W that correspond to the principal eigenvectors of ∑^-1_W∑_B. The regularization is needed because for small samples size, ∑_W cannot be inverted directly. Then, the solution would be reformulated as is expressed in the next equation, where Λ is the eigenvalues matrix (a diagonal matrix) as is presented in (7):

After data weighting by obtaining XD, where D be a diagonal matrix, the function to optimize is transformed in (8):

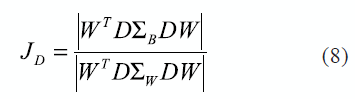
Weighted variables and relevance criteria

In previous subsections some weighted linear transformations were defined. Now, the interest is to project data in a f dimension space. Such dimension depends on the chosen rotation criterion; for instance, there is a bi-class problem and the convergence of WRDA is required, the fixed dimension must be f=1, in order to reach the convergence. For evaluating the weighted projection relevance at a fixed dimension, the measurement of separability is required. The parameter to be optimized is the weight diagonal matrix D, and the selected criterion is the inter-classes and intra-classes dispersion matrix traces coefficient, known as J₄ [20]. For projected and weighted data, this measurement is given by (9):

where ф can represent U or W. The size of ф is c x f and f denotes the fixed dimension, corresponding to the number of projection vectors ф such that: ф = (ф₁, ф₂,…, ф_f).

Rewriting the D matrix as a column vector d, and using the Hadamard matrix product (expressed as o), the traces of equation (9) can be rewritten as is presented in (10):

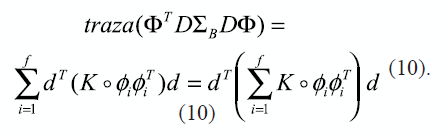
Then, equation (9) is transformed in equation (11):

This function is essentially equal to the LDA (linear discriminant analysis) function, then, the solution of d with norm L₂, will be chosen by the principal eigenvector given by (12):

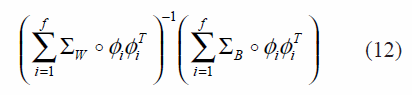
Note that this kind of description assumes that the ф elements are static; this problem is overcome by overlapping d and ф calculation, until the convergence of both is reached [9]. Related to weight interpretability, in order to define the dispersion, positive values are generally required. Nevertheless, in the context of relevance function used in this work, negative values can be obtained, this is avoided taking the absolute value of d.

Weighted reduction WPCA and WRDA

In [9] the convergence towards local maximum, using the power method applied to Q-α method which objective function is similar to J₄ is shown. Such proof was carried out for a particular case, where the objective function is poor, which means that there is a subset of characteristics including a coherent cluster and a positive function, conditions that normally can not be demanded. For this reason, in this section the convergence objective function in WPCA is proved, but it requires using the lemma 1, which can be demonstrated from two perspectives: analytic and algebraic.

The next lemma guaranties the objective function has a maximum. Moreover, it is observed that any search method converges to the same limit.

Lemma: The objective function 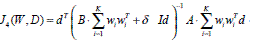has a maximum.

Proof (analyticversion): the objective function can be represented as: J (W, D) = (d, Γw (d) where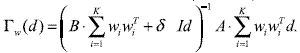

Let be C = { (d, Γ_w (d)) : ||d|| = 1} a set. The set is not empty since any eigenvector d = β_i satisfies the condition in the C set. Now, it is necessary to show that the set posses supremum. Taking a base of eigenvectors { β₁, β₂,…,β_n} , associated to the transformation Γw then, for any d vector conformed by a linear combination of  β_i  i it is had that d = ∑ⁿ_i=1c_iβ_i, such that:

J(W,D)=(d,Γ_w(d)) =(∑ⁿ_i=1c_iβ_i,Γ_W(∑ⁿ_i=1c_iβ_i))= ∑ⁿ_i=1λ_ic²_i, where ||d||²=||∑ⁿ_i=1c²_i||>1. Then C is upper bounded, because of the supremum axiom sup(C) exists. Considering ||d||² = ∑ⁿ_i=1c²_i = 1 and λ = max_i≤i≤n{ λ_i} it implies that sup(C) = λ. For this reason, if d = β the eigenvector associated to the greater eigenvalue λ, maximizes the objective function.

Proof 2 (algebraic version): The objective function J(w,D) = trace(W^T DADW) is maximized, under restrictions: W^TW=Id, trace(W^TDBDW) = 1 where D be a diagonal matrix and ||d|| = 1. The original data is stored in the X matrix and its covariance X^TX is analyzed, written it as X^TX = A + B , being A and B symmetric and positive semidefined matrixes, which can be substituted by Cholesky decomposition: X^TX = A^T₁A₁ + B^T₁B₁. Multiplying the left side by W_TD and the right side by DW and taken the traces, next expression is obtained: J(W,D) = traza(W^TDA^T₁A₁DW) = traza(DA^T₁A₁DWW^T). Using the W orthogonality conditions, it can be written as J(W,D) = traza(DA^T₁ A₁D)= ||A₁D||²_F.

Finally it can be expressed as J(W,D) = ||[d₁A₁(1,:), d₂A₁(2,:),…,d_nA₁(n,:)]^T||²₂. Its matrix representation is given by:

Then, trace (W^TDB^T₁B₁DW) = 1 implies that ∑d²_iB₁(:,i)^TB₁(:,i) = 1, and it can be transformed in ∑d_i˜ = 1 where ∑d_i˜ = d_iy_i such that y_i =B₁(:,i)^TB₁(:,i). Therefore D can be expressed in a matrix form as:

The last expression can be transformed in the next function for maximizing: J(W,D) = ||Md||²₂, joined to ||d|| = 1, which has as a maximum ||M|| as is evident.

Following, the WPCA algorithm and its convergence is presented.

WPCA algorithm

The iterative nature and its convergence of EM and PCA probabilistic parameters estimation is used for obtaining the WPCA algorithm, which is described as follow, employing r as the iteration index:

i   Normalize each characteristics vector for obtaining zero mean and the one Euclidean norm (||x||₂ = 1).

ii   Start with some orthogonal set of vectors U⁽⁰⁾.

iii   Calculate D^(r) from the solution given in equation (12) and weighted data.

iv   Calculate the step-E and step-M, from equation (4) and (5) respectively. Normalize the C columns de C for obtaining ||C(:,i)||₂ = 1.

v   If ||C^(r) - C^(r-1)||₂ > ε, return to numeral iii.

vi   Orthonormalize the subspace obtained, finding its singular values decomposition (SVD), as follow: SVD(C^TDX^TXDC) = ASA^T, C_final= A^TC where A, S the elements obtained from the decomposition SVD.

WPCA convergence

As was stated in the last section, weighting the characteristics by integrating with EM method can guarantee the convergence of steps D, and it is possible to ensure the relevant features obtained. From equation (4) the relationship (13) was reach in the algorithm:

Again, r corresponds to the iteration. As EM is applied (increasing r) the perturbation V^(r) decreases, due to it is approximated to the most discriminant axes. That is, if r → ∞, then || V^(r)|| → 0, guarantying the convergence.

Theorem 1: If C(r)→ Cˆ y Z^(r)→ Zˆ then D^(r)→ Dˆ.

Proof: Given the Eq. (13) for iterations r and r + 1, the subtraction produces: (D^(r+1) -D^(r))X = (C^(r+1)Z^(r+1) -C^(r)Z^(r)) + (V^(r+1) - V^(r)) . Applying to the last relationship, any type of norm follows: ||(D^(r+1) -D^(r))X|| ≤ ||C^(r+1)Z^(r+1) - C^(r)Z^(r) + V^(r+1) - V^(r)||. It is known that if r → ∞, then || V^(r)|| → 0, then: ||(D^(r+1) -D^(r))X|| ≤ ||C^(r+1)Z^(r+1) - C^(r)Z^(r)||. Adding and subtracting C^(r+1) Z^(r),to the right side, it is obtained||(D^(r+1) -D^(r))X|| ≤ ||C^(r+1)(Z^(r+1) -Z^(r)) + (C^(r+1) –C^(r))Z^(r)|| Applying the triangular inequality and the multiplicative property, the expression: ||(D^(r+1) -D^(r)) ||||X||≤|| C^(r+1)|||| (Z^(r+1) -Z^(r))||+ || (C^(r+1) –C^(r))|||| Z^(r)|| is reached, when r → ∞, then ||(D^(r+1) -D^(r)) ||||X||≤|| C^{^}|||| (Z^(r+1) -Z^(r))||+ || (C^(r+1) –C^(r))|||| Z^||  By hypothesis, X is the original data matrix, then ||X|| > 0. In a norm space, if a sequence converges, is a sequence of Cauchy. If r → ∞, then ||C^(r+1) –C^(r)||→ O, ||Z^(r+1) -Z^(r)||→ O, and ||D^(r+1) -D^(r)||→ O. Thus the weight convergence working in a Banach space is had.

WRDA Algorithm

For this algorithm, errors produced by the rotation of weighted data are not important, since not only the function of each rotation but also the weighting function have similar directions. The algorithm is described as follow:

Fix the k - 1 dimension, being k the number of classes.

Normalize each vector of feature for having media zero and Euclidian norm one.

Start with some orthogonal set of vectors W⁽⁰⁾.

Calculate d^(r) from the solution of equation (12), weighting the data.

Calculate the W^(r) from equation (8) y (9).

If ||W^(r)-W^(r-1)||₂ > ε, return to numeral iii. ε is the fixed error in the process.

Its objective function is precisely the observed in the lemma 1.

Results and analysis

By using a support vectors machine (SVM) classifier and evaluating its performance using two different approaches: employing ROC curves and hyper-surfaces and using the classification error, the dimensionality reduction PCA, PPCA, WPCA y WRDA techniques behavior was studied. Real data generated from geometric features as area, perimeters, orientations, dispersion, centroids and different statistical moments were used, obtaining 70 features applied to 50 capillary images of people without lupus erythematosus and 50 capillary images of ill people. In figure 1, data projection on the principal plane is shown. It is observed that in WPCA and WRDA methods, the data clouds belonging to healthy people class (circle) versus lupus erythematosus ill people class (cross), are more compacted. They vary between -0.1 and 0.1 on the horizontal axis and take values between -0.04 and 0.04 on the vertical axis. While in PCA and PPCA methods, the clouds are enlarged and the horizontal axis varies between -0.5 and -0.5 and the vertical axis varies between -0.3 and 0.2.

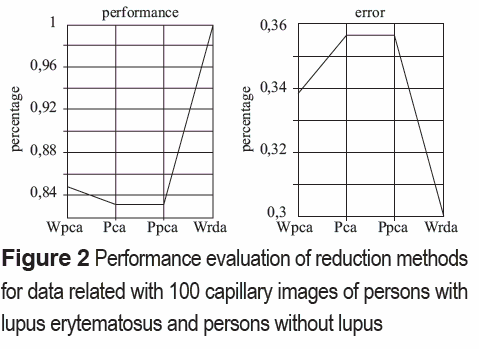
In figure 2, the reduction methods performance is shown. In the left curve, the highest point indicates that WRDA obtained the greatest efficiency percent, while the right curve shows that WRDA has the lowest classification error compared with the other methods.

The figure 3 shows the reduction methods performance in the classification applied to 70 databases discharged from the website [21]. From the figure, it is observed that the WRDA method presented the best performance compared to the others methods.

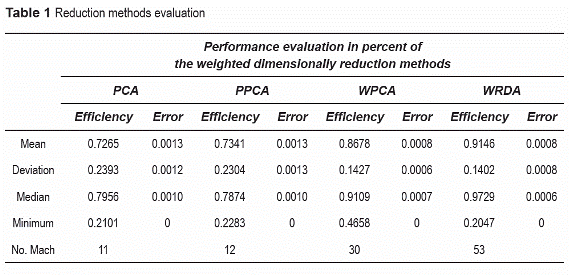
In table 1, the performance behavior and classifier errors of reduction methods applied to 70 databases were summarized. The values were obtained by using the mean, median, standard deviation and minima. In row "number of match" a best performance for WRDA was observed in 53 of the 70 databases, while PCA and PPCA were the worst.

Conclusions

Proofs of WPCA and WRDA reduction methods were carried out from two points of view: algebraic and geometric. Such proofs were relatively weaker than those known for other weighted methods. Results of weighted reduction methods PPCA, WPCA and WRDA performance were present. These results indicate that WRDA method has a best performance in 75% of databases, being the first compared to the other methods. In the literature, no rigorous proofs of the WPCA method and its variants are reported. For this reason, great part of the document was dedicated to carry out formalization tests, one analytic and other algebraic.

Capillary images showed great complexity for extracting relevant features due to the signal noise ratio. The feature reduction methods implemented in this paper. It was confirmed by the errors generated in the order of 30%. It can be observed since the classes were highly overlapped. Nevertheless, the method with the best performance was WRDA, reducing the classification error in spite of the classes overlapping.

Acknowledgments

Authors grateful the economical support of Colciencias y CONACyT in the Project 364, and to Dima for the Project "Herramienta para soporte al diagnóstico de la enfermedades vasculares usando imágenes capilares", and to Cristian Ocampo Blandón for carrying out the graphic interface in the dimensionality reduction process.

References

1. B. A. Olshausen, D. J. Field. "Emergence of simple-cell receptive field properties by learning a sparse code for natural images". Nature. Vol. 381. 1996. pp. 607- 609.         [ Links ]

2. C. M. Bishop. Pattern recognition and machine learning. Ed. Springer. New York. 2006. pp. 1-738.         [ Links ]

3. M. E. Tipping, C. M. Bishop. "Mixtures of probabilistic principal component analyzers". Neural Computation. Vol. 11. 1999. pp. 443-482.         [ Links ]

4. A. Sharma, K. K. Paliwal, G. C. Onwubolu. "Pattern Classification: An Improvement Using Combination of VQ and PCA Based Techniques". American Journal of Applied Sciences. Vol. 2. 2005. pp. 1445-1455.         [ Links ]

5. J. C. Burges. "Geometric Methods for Feature Selection and Dimensional Reduction" in: O. Maimon, L. Rokach. (editors). Data Mining and Knowledge Discovery Handbook: A Complete Guide for Practitioners and Researchers. Ed. Springer. New York. 2006. pp. 59-91.         [ Links ]

6. L. K. Saul, K. Q. Weinberger, J. H. Ham, F. Sha, D. D. Lee. "Spectral methods for dimensionality reduction". In: O Chapelle, B. Schölkopf, A. Zien. (editores). Semisupervised Learning. Ed. MIT Press. Cambridge. Massachusetts. USA. 2006. pp. 279-294.         [ Links ]

7. J. Venna. Dimensionality reduction for visual exploration of similarity structures. PhD thesis. Helsinki University of Technology. Helsinki. 2007. pp. 11-32.         [ Links ]

8. L. V. Maaten, E. Postma, J. V. Herik. "Dimensionality Reduction: A Comparative Review". Elsevier Journal of Machine Learning Research. Vol. 10. 2009. pp. 1-41.         [ Links ]

9. L. Wolf, A. Shashua. "Feature Selection for Unsupervised and Supervised Inference: The Emergence of Sparsity in a Weight-Based Approach". Journal of Machine Learning Research. Vol. 6. 2005. pp. 1855-1887.         [ Links ]

10. A. Blum, P. Langley. "Selection of relevant features and examples in machine learning". Artificial Intelligence. Vol. 97. 1997. pp. 245-271.         [ Links ]

11. M. A. Turk, A. P. Pentland. "Face Recognition Using Eigenfaces". Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Maui. Hawaii. USA. Vol. 1. 1991. pp. 586-591.         [ Links ]

12. G. Balcerowska, R. Siuda. "Inelastic background subtraction from a set of angle-dependent XPS spectra using PCA and polynomial approximation". Vacuum. Vol. 54. 1999. pp.195-199.         [ Links ]

13. W. Deng, J. Hu, J. Guo, W. Cai, D. Feng. "Robust, accurate and efficient face recognition froma single training image: A uniform pursuit approach". Pattern Recognition. Vol. 43. 2010. pp. 1748–1762.         [ Links ]

14. Q. Zhao, H. Lu, D. Zhang. "A fast evolutionary pursuit algorithm based on linearly combining vectors". Pattern Recognition. Vol. 39. 2006. pp. 310-312.         [ Links ]

15. L. G. Sánchez-Giraldo, F. Martínez-Tabares, G. Castellanos-Domínguez. "Functional Feature Selection by Weighted Projections in Pathological Voice Detection". Lecture Notes in Computer Science. Vol. 5856. 2009. pp. 329-336.         [ Links ]

16. L. G. Sánchez-Giraldo, G. Castellanos-Domínguez. "Weighted feature extraction with a functional data extension". Neurocomputing. Vol. 73. 2010. pp. 1760- 1773.         [ Links ]

17. D. Skocaj, A. Leonardis. "Weighted and robust incremental method for subspace learning". Proceedings of the Ninth IEEE International Conference on Computer Vision. Vol. 2. 2003. pp. 1494-1501.         [ Links ]

18. M. Tipping, C. Bishop. "Probabilistic principal component analysis". Journal of the Royal Statistical Society. Series B. Vol. 61. 1999. pp. 611-622.         [ Links ]

19. J. H. Friedman. "Regularized discriminant analysis". Journal of the American Statistical Association. Vol. 84. 1989. pp. 165-175.         [ Links ]

20. A. R. Webb. Statistical Pattern Recognition. 2^a. ed. Ed. John Willey and Sons. London. 2002. pp. 305-360.         [ Links ]

21. C. Lai. W. J. Lee. M. Loog. P. Paclik. D. Tax. URL:http://ict.ewi.tudelft.nl/~davidt/occ/index.html. Consultada el 1 de Julio de 2009.        [ Links ]

(Recibido el 17 de diciembre de 2009. Aceptado el 31 de agosto de 2010)

^*Autor de correspondencia:correo electrónico: jcrianoro@unal.edu.co (J. C.Riaño)