Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.58 Medellín Apr./June 2011
Control difuso adaptativo aplicado a un sistema de fermentación de flujo continuo de alcohol
Adaptive fuzzy control applied to a fermentation system of continuous alcohol flow
Andrés Escobar Díaz, Cesar Hernández*, Juan Pablo Arguello Fajardo
Universidad Distrital Francisco José de Caldas, Facultad de Tecnología, Transversal 70 B N. 73 a 35 sur. Bogotá, Colombia
Resumen
La técnica de control FRMLC, control difuso con aprendizaje y modelo de referencia se ha estudiado como método para sintonizar controladores difusos. Su desempeño se ha evaluado en un sistema de fermentación de flujo continuo de alcohol el cual tiene como característica una dinámica no lineal sujeta a variación de parámetros en el tiempo. Se utiliza un método de sintonización innovadora, la cual implica un desarrollo sobre Matlab que facilita estudiar la técnica de control FRMLC. Esta herramienta de software permitió construir metodologías de sintonización mas estructuradas para la aplicación de esta técnica en diferentes procesos.
Palabras clave: Aprendizaje, controlador, lógica difusa, control adaptivo, inferencia, modelo inverso, estrategias de sintonización.
Abstract
The FRMLC, Fuzzy Reference Model Learning Control has been studied as a method for tuning fuzzy controllers. Its performance has been evaluated in a fermentation system with continuous alcohol flow which is characterized as a non lineal dynamics. Parameters vary with time in non lineal dynamics. A method of innovative tuning was employed which implicates a Matlab development that facilitates the study of the control technique FRMLC. It allowed building tuning methodologies for the application of that technique in different processes.
Keywords: Learning, controller, fuzzy logic, adaptive control, inference, inverse model, strategy of tuning.
Introducción
En años recientes el control difuso ha emergido como una alternativa frente al control clásico, especialmente cuando se requiere controlar sistemas no lineales, que presentan dificultad a la hora de ser identificados. El diseño de un control difuso es usualmente realizado por un experto el cual plasma su conocimiento de la planta en la elección de parámetros como la distribución de funciones de pertenencia; los operadores usados para realizar la Borrosificación-Desborrosificación, reglas, agregación e implicación entre otros. [14]. El controlador difuso puede responder inadecuadamente si el planteamiento de dichos parámetros no se encuentra acorde con la dinámica de la planta, mas cuando esta tiene comportamientos no lineales, en este caso se hace necesario el uso de algún método de sintonización el cual encuentre los parámetros del control para manejar adecuadamente la planta.
Para los que han sintonizado controladores difusos manualmente, de acuerdo a su experiencia, conocen lo tedioso que es manipular los parámetros del controlador difuso para que el desempeño del sistema de control sea el adecuado y más cuando el proceso a controlar tiene comportamientos altamente no lineales. Por esto surge la necesidad de tener una herramienta de sintonización más expedita y automática para el cálculo de los parámetros del controlador. También surge la necesidad que el control detecte diferentes puntos de operación en el proceso que se quiere controlar, cuando este tiene comportamientos no lineales, y que adecue la señal de control de acuerdo a estos. Una de las técnicas que tiene las características anteriores recibe el nombre de FRMLC (Fuzzy Reference Model Learning Control). [4-7].
En la literatura especializada sobre FRMLC no se encuentra con detalle los métodos de ajuste y sintonización para esta técnica. En este artículo se desarrolla un software sobre Matlab que permite, simular la técnica FRMLC y encontrar procedimientos más claros para el uso y sintonización de esta. Primero se explica la técnica FRMLC. Luego se muestra el proceso que se utiliza para probar la técnica y se muestran los resultados: el software desarrollado y las metodologías de sintonización. Por último se muestran conclusiones y posibles trabajos futuros.
FRMLC
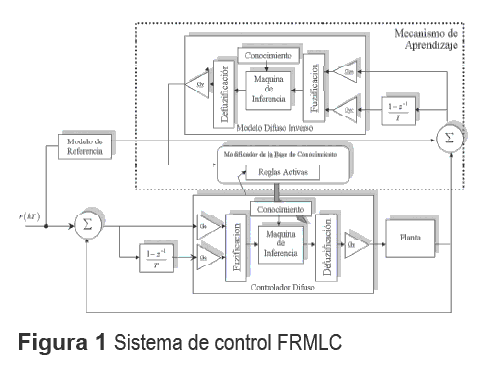
El sistema de control FRMLC tiene como principal objetivo llevar a cabo la sintonización de un controlador difuso. Se compone de un conjunto de elementos: el controlador difuso, el mecanismo de aprendizaje, el modelo de referencia y el modelo inverso de la planta, figura 1.
El controlador difuso es similar a cualquier otro controlador difuso, excepto por su capacidad para ser modificado en tiempo real de ejecución. Este toma el error, entre la referencia r(kt) y la salida del proceso, y la derivada del error para decidir cuanta energía envía a la planta; para hacer que la salida del proceso llegue a ser igual a la referencia. El modelo de referencia es el que indica cómo se debe comportar dinámicamente todo el sistema de control. En cuanto al mecanismo de aprendizaje, este se compone de dos partes principales, siendo la primera de ellas el modelo difuso inverso de la planta y en segundo lugar el modificador de la base de conocimiento del controlador difuso. El modelo inverso deduce cuanto debe modificase la señal de control para que la salida de la planta sea igual al modelo de referencia. El modificador de la base de conocimiento cambia la ubicación de las funciones de pertenencia de los consecuentes de las reglas del controlador para que la señal de control sea la que dice el modelo inverso. [5-7].
El funcionamiento de FRMLC se puede resumir de la siguiente manera: El modelo inverso toma la salida del modelo de referencia y la planta, si estas señales no son iguales, este deduce cuanto debe ser la señal de control apropiada. El modificador de la base de conocimiento cambia el controlador para que la señal de control llegue a ser la que dice el modelo inverso. En el control difuso queda almacenado como debe responder de acuerdo a las variaciones de comportamiento de la planta y variaciones con respecto a la referencia de tal forma que se pueda calcular correctamente la señal de control que debe enviarse a la planta.
Controlador difuso
El controlador difuso es un sistema de inferencia difuso (SID). Las entradas al controlador difuso o universos de entrada generalmente son el error y la variación en el error aunque se puede usar cualquier otra variable del proceso. El error y la variación o derivada discreta del error se pueden definir como en la ecuación 1 y la ecuación 2 respectivamente.
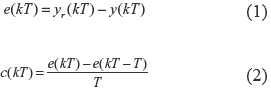
Donde yr(kT) denota la salida deseada del proceso y y(kT) denota la salida de la planta. Todas las señales son discretas. T es el periodo de muestreo. Las reglas del controlador son una relación difusa de la forma:
Si error es bajo y deriva es baja
Entonces Señal de Control es baja
El controlador difuso contiene varias reglas difusas, veinticinco: que resultan de combinar cinco conceptos en cada universo de entrada. Estas reglas conjuntamente generan una acción de control a partir del error y la variación del error. Las operaciones difusas que se utilizan son: unión y agregación: máximo, implicación e intersección: mínimo, desborrosificación: promedio de centros, borrosificación: singleton.
Modelo de referencia
El modelo de referencia define dinámicamente la respuesta deseada en el proceso y establece sobre el sistema la estabilidad, tiempo de asentamiento y sobre impulso. El modelo de referencia puede representar casi cualquier dinámica. Con el uso de un modelo de referencia se busca suavizar los cambios en la referencia, para evitar cambios bruscos en el sistema y no generar referencias que resultan imposibles de seguir. Un ejemplo de modelo de referencia es la función de transferencia de un sistema de segundo orden típico, pues con la constante de amortiguamiento y frecuencia natural no amortiguada se define el tiempo de establecimiento y máximo sobre impulso.
Modelo difuso inverso
El modelo difuso inverso es otro SID. Los universos de entrada son dos: el error entre la salida del modelo de referencia, ym(kT), y la salida de la planta. El otro universo de entrada es la derivada discreta del error anterior, yc(kT) como se observa en la ecuación 3.

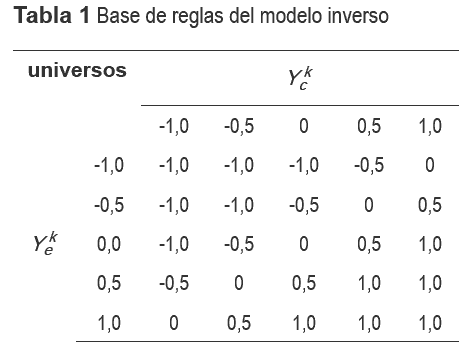
La señal ye(kT) es el error del sistema con respecto al modelo de referencia. Con base en el error y derivada anteriormente definidos, el modelo inverso calcula cuanto debe ser modificada la señal de control para aplicar a la planta de tal forma que se pueda hacer que la salida de la planta siga la salida del modelo de referencia. Las reglas del modelo inverso son una relación difusa de la forma: tabla 1.
SI error ye(kT) es bajo y deriva yc(kT) es baja entonces la corrección en la señal de control es baja
El modelo difuso inverso busca proveer al sistema un conocimiento acerca de la dinámica de la planta; se enfatiza en que no es necesario caracterizar la dinámica inversa con precisión, sólo se necesita una representación aproximada.
La tabla 1 muestra una base de reglas típica para un modelo inverso con 5 funciones de pertenencia por universo, las entradas son el error ye(kT) y la derivada del error yc(kT). '0' es cero, '0,5' es bajo, '1' es alto, '-0,5' es bajo negativo y '-1' es alto negativo. Se puede apreciar el valor mapeado para diversos valores de error y variación del error en las primeras celdas verticales y horizontales; en las celdas centrales se encuentra el valor de salida del modelo inverso o factor de corrección p(kT). Cada celda interna en la tabla 1 muestra una regla del SID que representa el modelo inverso. Este factor de corrección es lo que hay que adicionar para alcanzar la señal de control adecuada.
Modificador de la base de conocimiento
El modificador de la base de conocimiento realiza la función de cambiar el controlador difuso para lograr un mejor comportamiento influyendo sobre la señal de control. El modelo inverso le dice al modificador de base de reglas cuanto debe modificar, p(kT), la señal de control. El modificador cambia especialmente la posición de las funciones de pertenencia del universo de salida del control. Finalmente la señal de control es la que hace que la salida de la planta sea igual al modelo de referencia.
La salida del controlador deseada puede ser la indicada en la ecuación 4.
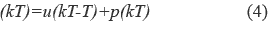
u(kT) es la señal de control actual y u(kT-T) es la señal de control en el periodo de muestreo anterior. Entonces la señal de control actual es la señal de control anterior más un factor de corrección p(kT). Para hacer que la señal de control se la que se quiere se modifican los centros de las funciones de pertenencia de universo de salida del control. A continuación se explica con brevedad. [8-12].
Desplazamiento de centros
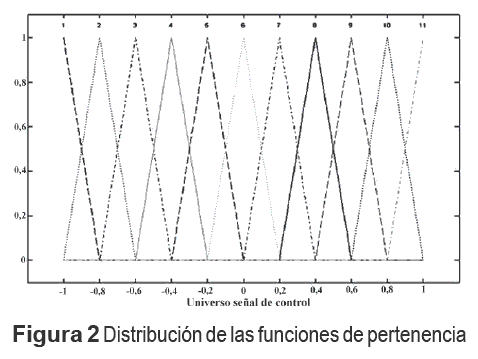
Se usa al principio funciones de pertenencias simétricas y uniformemente distribuidas en el universo de salida del controlador difuso. figura 2
bm denota el centro de dichas funciones de pertenencia. Estas funciones de pertenencia están presentes en las reglas del controlador difuso que contribuyen a la acción de control previa u(kT - T). Se realiza el proceso de actualización de la base del conocimiento en dos pasos. [8-12].
Se busca todas las reglas en el controlador difuso cuyo antecedente sea cierto o este activado, es decir:
mi(e(kT-T)),c(kT-T)>0
mi es el i-ésimo antecedente de regla, e es el error y c es la derivada del error. Con base en los valores de las entradas del control, error y derivada, se identifica un conjunto de reglas. A este conjunto se le da el nombre de "Conjunto activo" de reglas en el tiempo kT - T. Son estas reglas las que intervienen en el cálculo de la señal de control para este instante del tiempo y son las que se modifican.
Dado que bm(kT) denota el centro de la m-esima función de pertenencia de salida en el tiempo kT. Para todas las reglas del conjunto activo, se modifica la ubicación de la función de pertenencia del consecuente como se muestra en la ecuación 5.
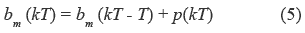
De esta forma se hace que la señal de control sea la adecuada para hacer que la salida del proceso sea igual a la salida del modelo de referencia y llegue a ser igual a la referencia. Las reglas que no se encuentren activas no son modificadas.
Materiales y métodos
Los reactores biológicos típicamente están gobernados por fuertes comportamientos no lineales, ocurridos tanto a escala macroscópica como microscópica. Las reacciones que toman lugar a éstas escalas pueden ocurrir a diferentes tasas dado que el biorreactor presenta múltiples condiciones tanto espaciales como temporales. [13].
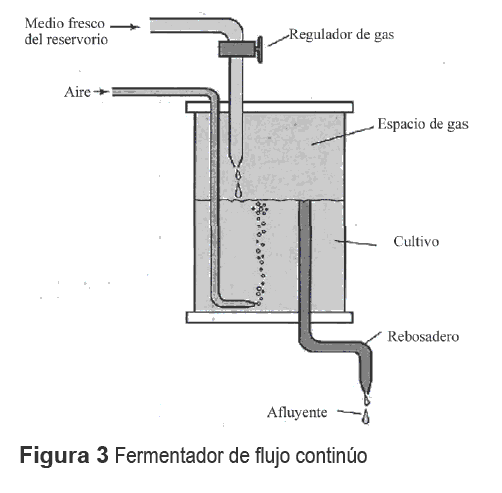
Un tipo especial de biorreactor es el de cultivo continuo; en este los microorganismos se mantienen en un crecimiento constante debido a que se añade continuamente medio de cultivo fresco que aporta nutrientes, y se va eliminando material usado, con el objeto de mantener el volumen del cultivo constante. En la naturaleza un ejemplo de cultivo continuo lo constituye el rumen de ciertos animales. El reto en un cultivo continuo consiste en mantener un ambiente constante durante todo el tiempo de cultivo.
Fermentación de flujo continuo
El biorreactor, figura 3, puede ser modelado usando las ecuaciones dinámicas descritas en la ecuación 6. [13]
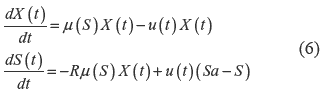
Donde
X: Concentración de biomasa
S: Concentración de substrato
u: Tasa de dilución
Sa: Concentración de substrato entrante
R: Coeficiente de rendimiento
μ: Tasa especifica de crecimiento.
La tasa específica de crecimiento se calcula en base a la ecuación de Monod, ver ecuación 7.
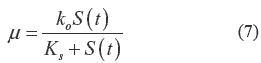
En esta ecuación koes la tasa de crecimiento máximo que puede alcanzar el microorganismo; el valor ks representa la concentración de substrato a la cual se alcanza una tasa de crecimiento igual a la mitad de la tasa de crecimiento máxima. La dilución relaciona la capacidad del tanque, volumen, con la velocidad del flujo entrante, como se indica en la ecuación 8.

Las entradas a la planta son el flujo entrante y la concentración de glucosa del flujo entrante, mientras que las salidas son la concentración de Biomasa, la concentración de substrato del flujo saliente y la tasa específica de crecimiento de los microorganismos.
Modo de operación
El biorreactor posee dos modos de operación dependiendo del producto que se desee obtener, cuando se utiliza en la fabricación de productos como vinagre o alcohol se conoce con el nombre de cultivo turbidostático, pues el objetivo del cultivo es mantener una concentración de substrato constante. Para productos como la levadura se cambia la variable a controlar ya que se desea mantener constante la densidad de población, este cultivo recibe el nombre de cultivo quimiostático. En ambos el elemento de control puede ser la concentración de flujo entrante, o la tasa de dilución.
Características variables
La concentración de biomasa se mide en (g/l) y puede tomar valores a partir de 0 y hasta el valor indicado en la ecuación 9.

La cantidad de biomasa producida se ve afectada por la concentración máxima de substrato que entra al tanque y por el coeficiente de rendimiento. La concentración de substrato del flujo saliente puede tomar valores que van desde 0 en el caso en el cual no hay ingreso de substrato o se consume todo el substrato, hasta el valor máximo del flujo entrante para el caso en el cual la tasa de dilución es 1. El rango para la concentración de substrato del flujo entrante no posee una limitante pero este valor puede ser alterado por el usuario, de ser así se elegirá un valor entre [0 2].
En cuanto a la tasa de crecimiento puede tomar valores desde 0 en el caso en el cual el cultivo se encuentra estancado por falta de substrato, hasta valores iguales a la tasa máxima de crecimiento, la cual se especifica en el modelo, pues resulta ser un parámetro que depende del tipo de microorganismo empleado en el proceso.
Resultados
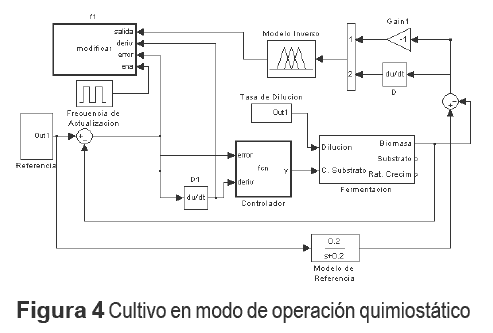
La figura 4 muestra la estructura del controlador implementada en Simulink; se puede apreciar que la salida del controlador es la dilución de la planta, y la variable realimentada es la concentración de substrato, también se puede apreciar que el ingreso de substrato limitante se ha dejado como una variable independiente con la cual se pueden realizar pruebas de desempeño del controlador ante una falta de suministro de substrato. La figura 4, es testigo de un desarrollo de software sobre Matlab [14] que implementa la estrategia de control FRLMC. Este desarrollo incluye una interface de usuario para configurar el sistema. En la herramienta se puede modificar todos los parámetros de la estructura de control como ganancias de los SID, rangos de las variables, funciones de pertenencia etc.
Como parámetros de la planta para la simulación fueron K0= 0,5, KS= 0,1, R = 2, Concentración de biomasa inicial = 0,01, Concentración de substrato = 0,5. Las pruebas se realizaron simulando los dos modos de operación del biorreactor. El sistema de control simulando el cultivo en modo de operación quimiostático se realiza con los siguientes parámetros: Rangos para el controlador: rango del error [-0,5 0,5], rango de la derivada del error [-0,3 0,3], rango de salida [0 3]. Rangos del modelo inverso: rango del error [-1,5 1,5], rango de la derivada del error [-1,5 1,5], rango de salida [-0,5 0,5]. Intervalo de actualización de la base de reglas 1seg. 5 funciones de pertenencia por universo; distribución de funciones uniforme. Actualización de la base de reglas por desplazamiento de centros.
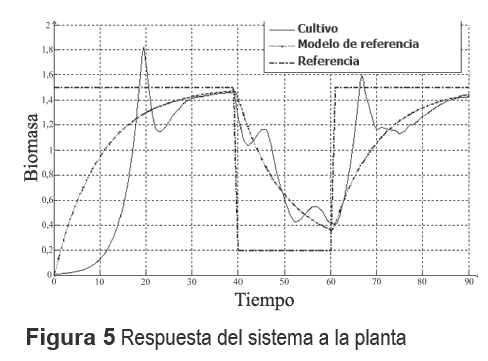
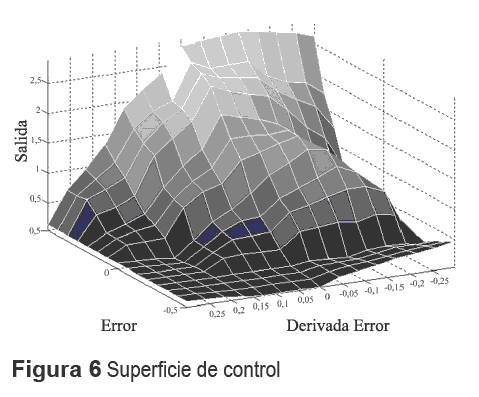
En la figura 5 se aprecia la interacción de la planta con el sistema, con el fin de entrenar la base de reglas. En la figura 6 se encuentra la superficie de control generada por el sistema al concluir la simulación.
Tal y como se puede apreciar en la figura 5, al principio el error es considerable, esto se debe a que al cultivo le lleva tiempo aumentar su población. Una vez generada dicha población se observa como la planta sigue la referencia.
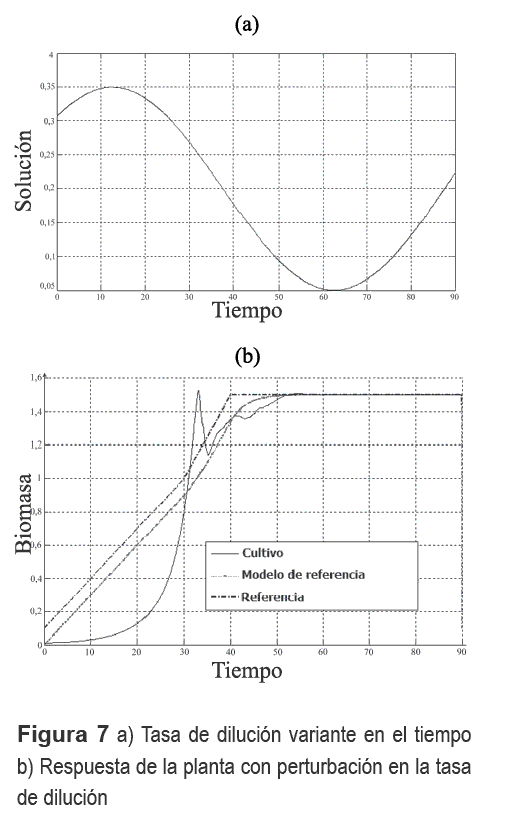
En la figura 7a se observa la dilución escogida con el fin de perturbar el comportamiento del cultivo, la figura 7b ilustra el comportamiento del cultivo al usar esta tasa de dilución y una referencia diferente a la escogida para el entrenamiento. Se observa que al comienzo de la simulación el crecimiento de la población es lento debido a la alta dilución, pero posteriormente esta disminuye, permitiendo que el controlador siga la referencia.
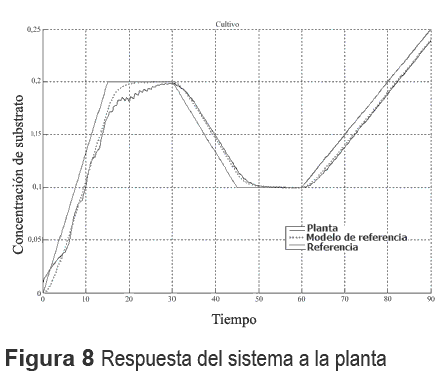
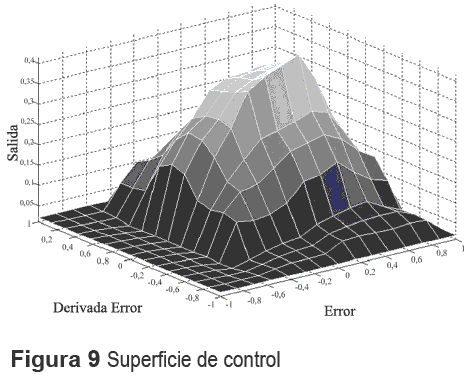
Para la simulación del funcionamiento del biorreactor en modo turbidostático, los parámetros que se tienen son: Rangos para el controlador: rango del error [-1 1], rango de la derivada del error [-1 1], rango de salida [0 0,5]. Rangos del modelo inverso: rango del error [-0,5 0,5], rango de la derivada del error [-0,5 0,5], rango de salida [-0,1 0,1]. Intervalo de actualización de la base de reglas 1seg. 5 funciones de pertenencia por universo; distribución de funciones uniforme. Actualización de la base de reglas por desplazamiento de centros. El sistema se configura a partir de los datos anteriores. En simulación se alimenta el sistema con una señal de referencia obteniéndose una respuesta como la observada en la figura 8, y generando una superficie de control como la mostrada en la figura 9. [15, 16, 17].
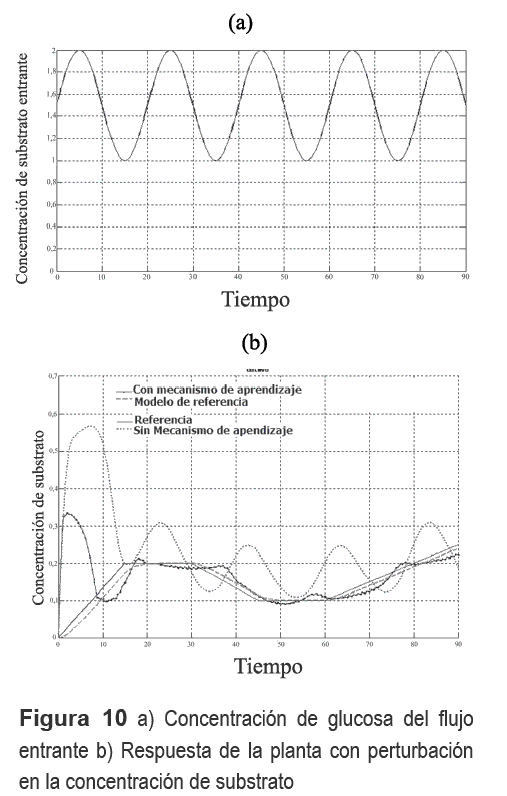
En la figura 10 podemos observar el comportamiento del sistema cuando hay variación en la concentración de flujo entrante; se puede apreciar que cuando el sistema no posee mecanismo de aprendizaje es incapaz de seguir la referencia debido al continuo cambio en la dinámica del sistema, mientras que cuando el mecanismo de aprendizaje se encuentra encendido hay un mejor seguimiento aunque la variación en la concentración causa oscilación en torno a la referencia. [18, 19].
Después de la verificación de la técnica con diferentes procesos se llegaron a propuestas para la construcción del sistema FRLMC y su sintonización.
Conclusiones
Aunque el modelamiento de sistemas con parámetros variantes en el tiempo puede llegar a ser muy complejo y su control aun mas, la técnica FRMLC evita el manejo matemático de estos sistemas, y facilita el diseño de un controlador apropiado, pues esta técnica se adapta tanto a los requerimientos del diseñador, como las condiciones impuestas por la planta. Como se ha podido apreciar el mecanismo de aprendizaje es indispensable cuando hay variación de parámetros o diferentes puntos de operación, puesto que el mecanismo de aprendizaje detecta estos cambios y hace cambiar el comportamiento del controlador para que el sistema en conjunto funcione de acuerdo a la dinámica especificada en el mecanismo de aprendizaje.
Es tipo de control se parece mucho más a un control ideal para un ingeniero en control. Conectar, que se auto sintonice y controle correctamente el sistema. Pues este tipo de se conecta al proceso que se quiere controlar, no se necesita conocer analíticamente la dinámica del sistema, pero si conceptualmente, hay que configurarle algunos parámetros y logra manejar todo el sistema. Este tipo de procedimiento que se sigue en este tipo de controladores es adecuado cuando se va a manejar sistemas no lineales.
Cuando se compara controladores clásicos difusos con el manejado en este articulo, se evita configurar las funciones de pertenencia de cada uno de los universos de entrada y de salida del controlador, configurar y crear las reglas. Con este tipo de control se utiliza una estructura general en gran parte del sistema y se cambian unos pocos parámetros que logran que el sistema se adaptable. Para quienes han sintonizado controles difusos clásicos, se dan cuenta que esto es un proceso tedioso. Este tipo de control hace todo el proceso de sintonización se reduzca a cambiar un conjunto pequeño de parámetros para adecuarse a las variables físicas y la dinámica del proceso que se quiere controlar, haciendo el paso de implementación y sintonización mucho más fácil.
Se han propuesto metodologías más detalladas para la creación y sintonización de la técnica de control FRLMC que no existían.
Como trabajos futuros: Adecuar la interfaces de software sobre Matlab, de tal forma que permita hacer pruebas con procesos reales; se quieren hacer implementaciones en hardware, en dispositivos lógicos programables, como FPGA's, los cuales reproduzcan esta técnica y permitan hacer pruebas en procesos reales. Estos trabajos están en etapa de desarrollo.
Referencias
1. K. Passino, S. Yurkovich. Fuzzy control. Ed. Addison-Wesley. California. USA. 1998. pp. 522-532. [ Links ]
2. G. Muñoz Quiñones, J. Ballén Salamanca. Diseño e implementación de un controlador difuso autosintonizado sobre microcontroladores, aplicado al control del péndulo invertido. Trabajo de pregrado. Universidad Distrital. Bogotá. 2003. pp. 68-89. [ Links ]
3. P. Antsaklis, K. Passino. An introduction to intelligent and autonomous control. Ed. Kluwer Academic Publishers. Norwell (USA). 1993. pp. 427-452. [ Links ]
4. W. Li-Xin. A course in fuzzy systems and control. Ed. Prentice Hall. New Jersey (USA). 1997. pp. 424-476. [ Links ]
5. R. L. Jeffey. "Fuzzy reference model learning control". Journal of Intelligent and Fuzzy Systems. Vol.4-1. 1996. pp. 33-47. [ Links ]
6. S. Abhishek. A multi-scale approach to fed-batch bioreactor control. Tesis de Maestría. Universidad de Pittsburgh. Pennsylvania (USA). 2002. pp. 71-88. [ Links ]
7. A. Kwong, M. Passino. "Dynamically focused fuzzy learning control". IEEE transactions on system man and cybernetics. Vol. 26. 1996. pp. 53-74. [ Links ]
8. L. Zadeh. The birth and evolution of fuzzy logic (FL), soft computing (SC) and computing with words (CW): a personal perspective. Ed. World Scientific Publishing Co. New Jersey (USA). 1996. pp. 819-843. [ Links ]
9. P. Dadone. Design optimization of fuzzy logic systems. Tesis de Doctorado. Virginia Polytechnic Institute and State University. Blacksburg. VA. 2001. pp. 64-97. [ Links ]
10. R. L. Jeeffey, K. Passino, S. Yurkovich. "Fuzzy learning control to antiskid braking system". IEEE transactions on control. Vol.1-2. 1993. pp. 122-129. [ Links ]
11. K. Tanaka, H. Wang. Fuzzy control system design and analysis. Ed. Jhon Wiley & Sons. New York (USA). 2001. pp. 320-361. [ Links ]
12. J. Mendel. "Fuzzy logic system for engineering: a tutorial". Proceeding of the IEEE. Vol. 83. 1995. pp. 345-377. [ Links ]
13. I. Queinnec, B. Dahhou, Y. Sevely. "Theoretical and experimental results in optimization of fedbatch fermentation process". Journal of Systems Engineering. Vol.1. 1991. pp. 31-40. [ Links ]
(Recibido el 5 de febrero de 2010. Aceptado el 31 de agosto de 2010)
*Autor de correspondencia: teléfono móvil: 311 218 66 35, fax: + 57 +1 + 731 15 25, correo electrónico: cahernandezs@udistrital.edu.co (C. Hernández)