Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230versão On-line ISSN 2422-2844
Rev.fac.ing.univ. Antioquia n.59 Medellín jul./set. 2011
Solving the traffic assignment problem using real data for a segment of Medellin's transportation network
Solución al problema de asignación del tránsito para un segmento de la red vial de Medellín a partir de datos reales
Carlos Alberto González Calderón1*, Guillermo González Calderón2, John Jairo Posada Henao3
1Universidad de Antioquia, Facultad de Ingeniería, Calle 67 N° 53-108. Bloque 20. Oficina 439, Medellín, Colombia.
2Grupo de Investigación ARKADIUS, Universidad de Medellín, Facultad de Ingenierías, Bloque 4, Medellín, Colombia
3Universidad Nacional de Colombia - Sede Medellín, Facultad de Minas, Calle 65 N° 78-28. Bloque M1. Oficina 113, Medellín, Colombia
Abstract
This paper is based on data obtained from most recent transportation studies done in the Metropolitan Area of Valle de Aburra, city of Medellin and other 9 municipalities. The studies were based on an Origin/Destination Survey (2005), Analysis of bus routes (2006), and Mobility Master Plan (2006). This paper explains the process of writing a software application for a given network (Network of Medellin) that solves the deterministic user equilibrium problem. The software code was implemented in Visual Basic .NET®, supported by some operations using Microsoft Excel®, and hardcoded for a segment of the Medellin network. The user equilibrium distribution of flow was found by using the Frank-Wolfe algorithm. The applied algorithm was analyzed in some aspects such as number of iterations, convergence patterns, response time, as well as changes in network demand. The traffic assignment models were analyzed by using the algorithm during the P.M. peak hour (hour of highest traffic congestion). The analysis was compared with the results from the traffic assignment procedure using TransCAD® (well-known and used transportation demand software) for the 2005 database and it was found that the software is somewhat faster than the algorithm, but the latter could be a good tool for practitioners and students for modeling small networks.
Keywords:Traffic modeling, traffic assignment, Frank-Wolfe algorithm.
Resumen
Este artículo está basado en datos obtenidos en los más recientes estudios de transporte que se han realizado en el Área Metropolitana del Valle de Aburrá. (Medellín y otros 9 municipios). Estos estudios fueron la Encuesta Origen Destino (2005), análisis de las rutas de buses (2005) y el Plan Maestro de Movilidad (2006). En el artículo se explica el proceso utilizado para el desarrollo de una aplicación informática para resolver el problema determinístico de equilibrio de usuario en la red vial de Medellín. El código fue construido usando Visual Basic.NET ® y Microsoft Excel ® para la ejecución de algunas operaciones en un segmento de la red vial de Medellín. La distribución del flujo del equilibrio de usuario fue encontrada usando el algoritmo de Frank-Wolfe y fueron analizados algunos aspectos tales como número de iteraciones, patrones de convergencia, tiempo de respuesta y cambios en la demanda de viajes en la red. Los modelos de asignación del tránsito fueron analizados para las horas pico de la tarde. Se compararon los resultados de la asignación del tránsito del algoritmo desarrollado en este trabajo con los resultados de TransCAD ® para los datos del 2005 y fue encontrado que el software es un poco más rápido que el algoritmo, pero sin embargo éste último puede ser una buena herramienta para profesionales y estudiantes para la modelación de redes pequeñas.
Palabras clave: Modelación de tránsito, asignación del tránsito,algoritmo Frank-Wolfe.
Introduction
Medellin is the second largest city in Colombia and it is located in Valle de Aburra; it has a population of 2.5 million people and has an area of 382 km2. Buses, taxis, and the "Metro de Medellin" (the only passenger municipal train system in Colombia) serve as public transportation services in the city. There are 4.8 million trips per day [1], where buses represent 34% of the trips, Metro de Medellin represents 10% of the trips, taxis and private automobiles represent 13% of the trips, and the other modes of transportation such as bicycles, walking, etc., represent 43% of the trips. Despite the variety of options, traffic in Medellin has become chaotic, as the number of vehicles has exceeded roadway capacity; the city has no further space for the construction of new highways or roads. For this reason and other mobility aspects like accessibility, the city needs an optimal traffic assignment for the transportation network to plan and forecast the traffic demand for future scenarios.
The use of the convex combinations method (Frank-Wolfe algorithm) in conjunction with the label-correcting (shortest path) algorithm for the direction finding step, provides an easy and efficient approach to minimizing the equivalent User Equilibrium (UE) program. The convergence of the convex combinations method is asymptotic in nature; the marginal contribution of each additional iteration to the reduction in the value of the objective function is decreasing, the number of iterations required for convergence is primarily a function of the congestion over the network, and the computational effort needed for each iteration is proportional to the number of origins and the size of the network [2]. Thus, the method can be implemented in a segment of the Medellin Network to obtain the traffic assignment by using the UE program and such is the purpose of this work.
Background
The convex combination algorithm was originally suggested by Frank and Wolfe in 1956 as a procedure for solving quadratic programming problems with linear constraints and is known also as the Frank-Wolfe (FW) method [2]. In the traffic application, the linear program decomposes into a set of shortest path problems [3].
The Frank-Wolfe method [4] was first introduced in quadratic programming at once it proved very effective for the resolution of large scale flood problems, with particularly interesting assets, resting on the marvelous fusion of the mathematical programming and the graph theory, the Frank-Wolfe method is famous for its advantages: it is easy to implement and it performs well far from the optimal solution. Unfortunately, its convergence rate is not entirely satisfactory; this slowness is due mainly to the way in zigzag described by the points of the algorithm showing very slow asymptotic convergence. To remedy this disadvantage, much of attempts have been done, since the first "L. J. Leblanc" works until recent works of "Ziyou Gao and Al" [5]. The Frank-Wolfe method is one of the most widely used algorithms for solving routing problems in the telecom and traffic areas [6], and it is widely used to solve traffic equilibrium assignment problems [2]. It has the characteristics of simple implementation and modest memory requirement. However, it also faces some problems such as slow convergence, no providing path information, and so on [7], i.e. the FW algorithm converges very slowly when iterations are closing to the optimal solution [2].
Sheffi [2] shows that the application of Frank and Wolfe's convex combinations method to the solution of transportation network equilibrium was first suggested by Bruynooghe in 1968 and applied by Murchland in 1969. Shortly thereafter it was used by LeBlanc in 1975, which coded and tested the algorithm for a small city. At the same time, Nguyen [8] suggested the use of the convex simplex method for solving the User Equilibrium equivalent minimization program.
Also Sheffi shows that Nguyen [8] also suggested the use of the reduced gradient method and a modified reduced gradient method for this purpose. In some side-by-side comparative experiments, Florian and Nguyen [9] found that even though the convex simplex method converges somewhat faster than the convex combinations method, it requires more computer memory. Consequently, the overall computational effort required by both methods is similar.
Methodology
Frank Wolfe Algorithm
In this study the traffic equilibrium is assumed to have additive path costs, users with perfect information, fixed demand, there is no link interaction in the network, and the cost functions are also monotonic, differentiable and continuous. The User Equilibrium (UE) objective function is given by equation (1): 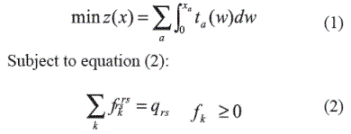
Where xa is the flow on link a, ta represents travel time on link a, fkrs represents the flow on path k connecting origin r and destination s, and qrs is the trip rate between origin r and destination s during the period of analysis.
The objective function is the sum of the integrals of the link performance functions. Applying the convex combinations algorithm for the minimization of the UE program requires, at every iteration, a solution of the linear program (LP) that decomposes into a set of shortest path problems. The steps of the Frank-Wolfe Algorithm can be expressed as:
Step 0: Initialization
Perform all-or-nothing assignment based on ta = ta (0) a. This yields {xa}. Set counter n = 1.
a. This yields {xa}. Set counter n = 1.
Step 1: Update
Set ta = ta (xa) 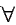 a
a
Step 2: Direction finding
Perform all-or-nothing assignment based on {ta}. This yields a set of (auxiliary) flows {ya}
Step 3: Line search
Find αn (0 ≤a≤ 1) that solves equation (3)
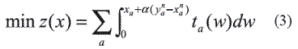
Set xan+1=xan+αn(yan-xan)
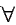 a
a Step 5: Convergence test
If a convergence criterion is met, stop (the current solution, {xan+1}, is the set of equilibrium link flows); otherwise, set n: = n + 1 and go to step 1.
Case study
This study takes place in the Metropolitan Area of the Aburrá Valley (Medellin city and other 9 municipalities) and it is based on data obtained on most recent studies of transportation. Those studies were Origin/Destination Survey (2005), Analysis of transit routes (2005), and Mobility Master Plan (2006) [1]. For this study, the traffic assignment was done taking into account the demand in PM peak hours (17:00 - 19:00) because is the time of the day with more congestion.
Zoning and Origin-Destination (OD) Matrix
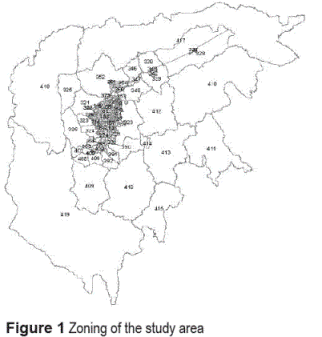
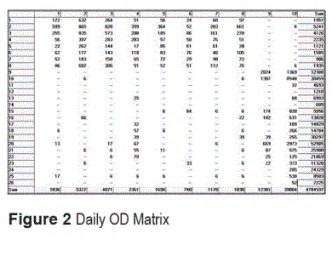
The traffic assignment models take as input flows between all origins and destinations. The OD Matrix in the study area is defined by 419 zones that are distributed as depicted in figure 1 [1]. Taking into account the information above and using the software TransCAD ®, figure 2 shows the OD matrix of all trips in all zones.The Network
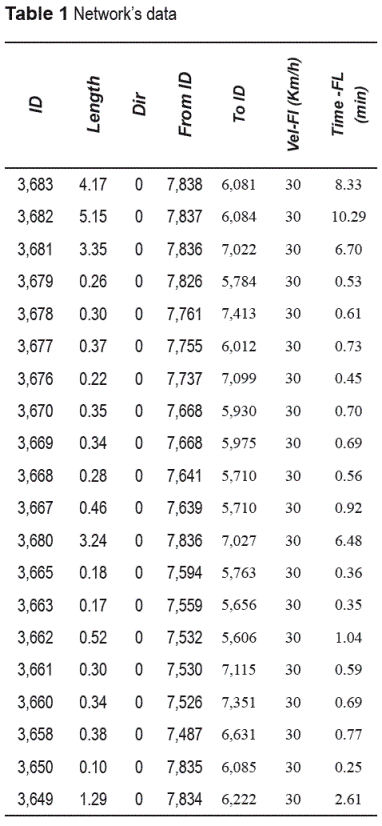
Medellin's network is composed by 1516 nodes and 4502 links connecting all nodes. In a common day, there are in Medellin 4.8 million trips [1], and those trips need a traffic network for the traffic assignment. Figure 3 shows the study network. Using TransCAD®, a network was built with links and nodes that include all 419 zones in the study area. The network contains data for links and nodes (See table 1) including travel time, velocity, length, direction, etc. [1]. For the purpose of this study there is a sample of a segment (selection) of Medellin's network and its structure (See figure 4). This network segment is composed by 13 nodes and 21 links connecting all nodes (See figure 5). The demand between origin 93 and destination 82 was 1,433 trips in the PM peak hour. The cost function used for the links in the network is given by Bureau of Public Roads (BPR) function equation (4): 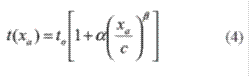
t (xa) = cost of using link a (given by time)
ta = free flow time
xa = flow on link a
c = capacity of the link
α,β = given parameters of the cost function. It is assumed that α = 0.15 and β =4
The Code
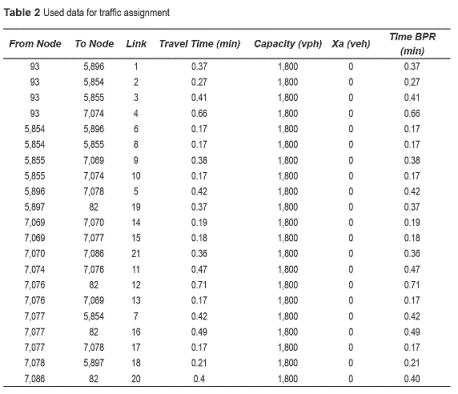
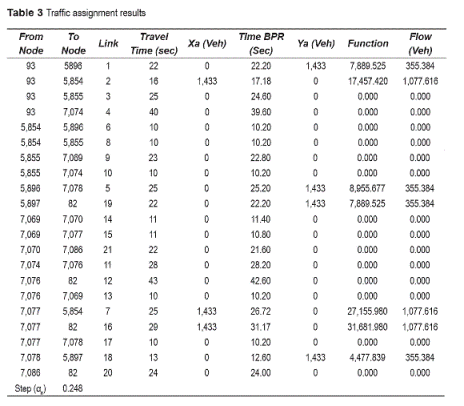
The code was implemented in Visual Basic .NET® and it was supported for some operations using Microsoft Excel. The first step of this process was to think in a way to make the program to understand the configuration of the network. The basic configuration of the code allows finding the shortest path using Dijkstra's algorithm [10] between an origin and a destination taking into account the costs (time) in all paths that connect this pair O-D. The algorithm essentially scans the network nodes in an iterative manner. At each iteration the algorithm tries to find a path from the root to the node being scanned that is better (shorter) than the current path. The data used for the algorithm is presented in table 2. The O-D pairs were introduced into the algorithm and the name of each vertex was modified with a new name called Element x, thus in instance, Node 93 (origin) is Element 0 and Node 82 (destination) is Element 12, and those values were organized as start element, end element and weight (variable cost). At the end, the Algorithm shows the previous vertex name.Excel was helpful in order to introduce the data and find some values such as step size and others. The results of the traffic assignment using Frank Wolfe algorithm (convergence criteria of 0.01 and using the shortest path with all or nothing assignment) are presented in table 3. The shortest path was presented as shown in figure 6, where it presented the first shortest path using all or nothing assignment. The Shortest Path from origin 93 to destination 82 is given by: 93-->5,854-->7,077-->82.
Traffic Assignment with TransCAD ®
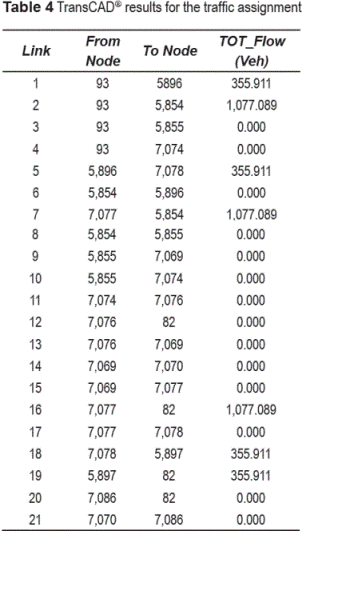
Using TransCAD ® and taking into account the data above was done the traffic assignment with the User Equilibrium method and convergence criteria of 0.01. The results are presented in table 4 and in table 5. The traffic assignment is depicted in figure 7 Results and discussion
Traffic Assignment varying of demand, alpha, beta and convergence
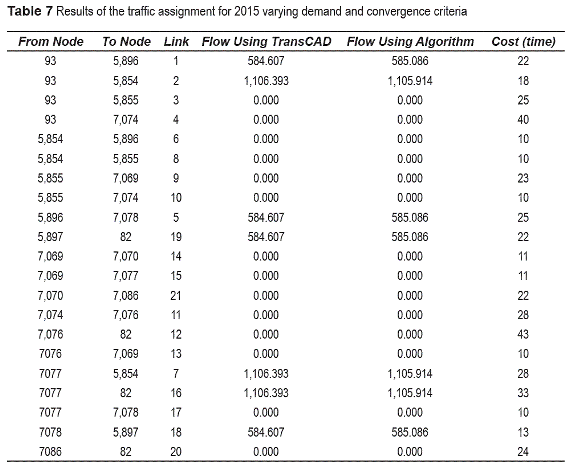
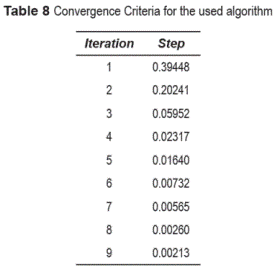
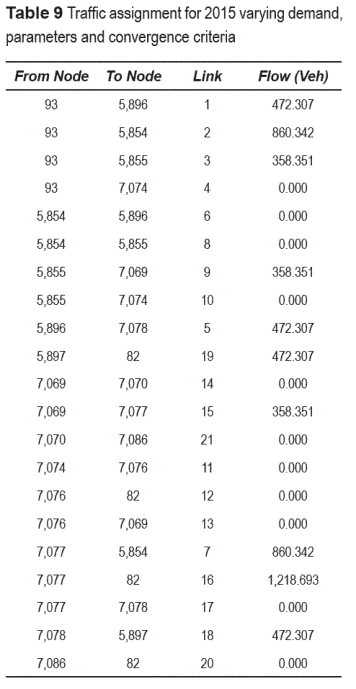
One important issue in transportation modeling is the forecasting process. For that reason in this paper we assumed a different value of demand between nodes 93 and 82. It is assumed that there will be 1,691 trips in 2015 (increase of 18%) instead of 1,433 trips. The traffic assignment was done using the User Equilibrium method and convergence criteria of 0.0001. Using the algorithm, the step size is alpha n = 0.3460 and using TransCAD ® is 0.3457. The result set of the traffic assignment in the segment of Medellin's Network is presented in table 7 Comparing the two result sets using TransCAD ® and the algorithm, the flow is very similar and the results are similar as in the previous case. Now, taking into account different convergence criteria of 0.05 and 0.001 and calibrated parameters from the network of alpha (0.68) and beta (2.2), the algorithm took 4 iterations for the convergence criteria of 0.05, and 10 iterations for the convergence criteria of 0.001. The results for the latter are presented in table 8 The results for the traffic assignment in the network varying demand, parameters and convergence criteria for 2015 are presented in table 9 Comparing the traffic assignments with variable convergence criteria and with new values of alpha and beta obtained from the calibration process, we can see that the flow paths are different from previous cases because it depends of the value of the step size; and it can be observed that if the convergence criteria is lower, the number of iterations increases significantly (from 4 to 10), and the step size reduces in each iteration until get the appropriate value with the same demand.Conclusions
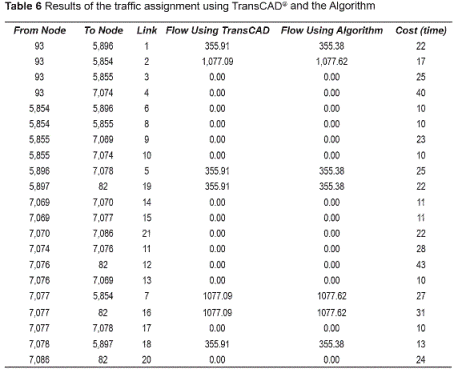
•This work introduces a software application in order to get the traffic assignment in a real network, with real demand and costs using Visual Basic .NET® and Excel ®. It was made for a segment of Medellin's Network and the results were compared with TransCAD ® results finding that TransCAD ® is a bit faster and shows graphically the path with the respective flows and costs, and has more accuracy in the results; but the algorithm can be used for modeling small networks and it is easy to use, besides of the cost of it (it is free). It could be useful for practitioners and students.
•All the flows found when the algorithm converged, satisfied the user equilibrium optimality condition. It explains that the network studied was in equilibrium and no user had any incentive to change their path choice because they would increase their travel costs in the network.
•The traffic assignment in this study took into account only travel time and capacity of the network. The values of Beta and Alpha were assumed. For best results it would be great to analyze more factors such as velocity, preloads, stops, etc. and use values of alpha and beta calibrated from the network. The purpose of this paper is to give an introduction to solve the traffic assignment in a real network but the code must be improved in order to get a better model of traffic assignment in any network.
•For different demands, the traffic assignment procedure used the same paths (the shortest path was always the same) in the network increasing only the flows in each link according to the traffic forecast. It could change it if is analyzed the entire network because the ratio of forecast of trips in all city is not the same.
•When there are various traffic assignments with variable convergence criteria the flow is different in both cases because it depends of the value of the step size; and if the convergence criteria is lower, the number of iterations increases significantly using the Frank-Wolfe Algorithm.
•Finally, it would be good to clarify that the algorithm implementation needs to improve the integration of Excel ® and Visual Basic. NET ® in order to get better results providing input mechanisms of all data required for the traffic assignment. Thus, it is recommended to continue actively working on the application user interface in order to facilitate the process of entering this information.
References
1. Área Metropolitana del Valle de Aburrá (AMVA) - Consorcio Movilidad Regional Colombia-Chile.Formulación del Plan Maestro de Movilidad para la Región Metropolitana del Valle de Aburrá. Medellín. 2007. Informe Final. Capítulo 2: Diagnóstico. pp. 102--188 [ Links ]
2. Y. Sheffi. Urban Transportation Networks: Equilibrium analysis with mathematical programming methods. Ed. Prentice-Hall Inc. New Jersey. 1985. pp. 111-132 [ Links ]
3. M. Patriksson. The traffic Assignment Problem-Models and Methods. Ed. VSP. Utrecht. 1994. pp. 131--135. [ Links ]
4. M. Frank, P. H. Wolfe. "An algorithm for quadratic programming". Naval Res. Logist. Quart. Vol. 3. 1956. pp. 95-110. [ Links ]
5. S. Arrache, R. Ouafi, "Improved Frank-Wolfe method: application to the traffic assignment problem". Proceedings of the International Congress of Mathematicians, Section 15. Madrid. 2006. pp. 8-9. http://www.icm2006.org/v_f/AbsDef/Posters/abs_1702.pdf. Consultada el 8 de septiembre de 2009. [ Links ]
6. S. Arrache, R. Ouafi. "Accelerating Convergence of the Frank-Wolfe Algorithm for Solving the Traffic Assignment Problem". IJCSNS International Journal of Computer Science and Network Security. Vol.8. 2008. pp. 181-186. [ Links ]
7. X. Meng, Q. Yunchao, G. Ziyou. "Implementing Frank-Wolfe Algorithm under Different Flow Update Strategies and Line Search Technologies". Journal of Transportation Systems Engineering and Information Technology. Vol. 8. 2008. pp. 14-22. [ Links ]
8. S. Nguyen. "An Algorithm for the Traffic Assignment Problem". Transportation Science. Vol. 8. 1974. pp. 203-216. [ Links ]
9. M. Florian, S. Nguyen. "An Application and Validation of Equilibrium. Trip Assignment Methods". Transportation Science Vol. 10. 1976. pp. 374-390. [ Links ]
10. E. W. Dijkstra. "A note on two problems in connexion with graphs". Numerische Mathematik. Vol. 1. 1959. pp. 269-271. [ Links ]
(Recibido el 16 de febrero de 2010. Aceptado el 31 de agosto de 2010)
*Autor de correspondencia: teléfono: + 57 + 4 + 219 55 70,fax: + 57 + 4 + 219 55 14, correo electrónico:gonzalez@udea.edu.co (C. González)