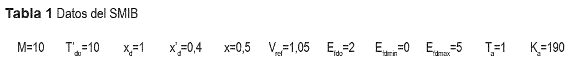Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.59 Medellín July/Sept. 2011
Análisis de bifurcaciones: Estudio comparativo sobre un sistema generador aislado - barraje infinito
Bifurcation Analysis: Comparative study over a single machine - infinite bus system
Sandra Milena Pérez Londoño1* , Gerard OlivarTost2, Fabiola Angulo García2
1 Universidad Tecnológica de Pereira, Programa de Ingeniería Eléctrica, Pereira, La Julita, Ciudad Universitaria, Eléctrica 214, Risaralda, Colombia
2 Universidad Nacional de Colombia, Departamento de Eléctrica, Electrónica y Computación, Cra 27 N.° 64-60 Manizales, Caldas - Colombia
Resumen
En este artículo se presenta la dinámica de un sistema simple conformado por un equivalente generador aislado conectado a un barraje infinito (denominado SMIB, por sus siglas en inglés Single Machine Infinite Bus), el cual presenta un limitador suave en el sistema de excitación. El sistema se somete a diversas condiciones de operación, con el fin de observar el comportamiento del mismo ante la aparición de bifurcaciones de codimensión-dos, específicamente la Zero-Hopf, que consigue ampliar la dinámica del sistema.
Palabras clave:Bifurcaciones, dinámica del sistema de potencia, estabilidad, limitador suave.
Abstract
In this paper, the dynamics of a straightforward system which includes a single machine-infinite bus power system (SMIB) with soft-limits in the field excitation control is presented. The system is forced to operate under several conditions for studying its behavior close to codimension-two bifurcation points. We specifically consider the Zero-Hopf bifurcation, which contributes significantly to the system dynamics.
Keywords: Bifurcations, power system dynamics, stability, soft limiter.
Introducción
El análisis de la estabilidad de un sistema de potencia se justifica, entre otros, por el aporte que realiza en el control, al identificar las condiciones operativas en las cuales el sistema puede colapsar. La teoría de bifurcaciones se utiliza para el análisis de sistemas de potencia, ya que éstos son inherentemente no lineales. Esta teoría asume que los parámetros varían lentamente y predice cómo y cuándo un sistema se torna inestable [1]. Existen bifurcaciones locales cuyos cambios estructurales son visibles cerca de un punto de equilibrio, una órbita periódica o, en general, un conjunto invariante. Entre ellas se encuentra la bifurcación de Hopf, en la cual un punto de equilibrio cambia su estabilidad y se generan oscilaciones (estables o inestables) [2]. Otro tipo de bifurcación es la denominada silla-nodo, en la cual, a medida que el parámetro varía, un punto de equilibrio estable desaparece al unirse con otro punto de equilibrio inestable y, como consecuencia, se puede presentar un colapso del sistema. Por otro lado, las bifurcaciones globales que relacionan fenómenos que ocurren en una amplia región del espacio de estados, son más difíciles de detectar y analizar, pero pueden suministrar información de cuándo un sistema de potencia puede tornarse inestable y/o presentar un comportamiento caótico [3].
Existen varias publicaciones en el análisis de bifurcaciones y caos en sistemas de potencia [3-7]. La mayoría, utilizan sistemas sencillos como el SMIB o de tres barras, ya que al aumentar su tamaño, se incrementa el orden del modelo y la complejidad de los fenómenos dinámicos que se presentan, haciendo su estudio más pesado computacionalmente. Entre algunas de las referencias, en [4] los autores utilizan un sistema de tres nodos con un modelo de carga dinámica y un modelo clásico para el generador para analizar bifurcaciones y caos. En [5] se analiza la inestabilidad de un sistema SMIB al incluir un limitador no suave en el excitador. En [3] los mismos autores analizan el efecto de incluir un sistema de control en la excitación de la máquina y muestran la presencia de una sucesión de bifurcaciones de doblamiento de periodo, que causa comportamiento caótico a medida que disminuye el coeficiente de amortiguamiento del sistema. En [6] se analizan las bifurcaciones de un sistema de nueve barras, con una complejidad considerable. En cuanto al análisis de bifurcaciones denominadas de codimension-dos (aquellas que se pueden presentar en un sistema como consecuencia del aumento de la dimensión de la variedad centro, o a la falla de algunas de las condiciones de no degeneración), los autores en [7], analizan en un sistema de tres barras, la presencia de la bifurcación Bogdanov-Takens y los fenómenos dinámicos que se presentan alrededor de ella.
En el presente artículo se utiliza el modelo dado en [5], pero con el fin de no sobrepasar los límites de funcionamiento de la máquina, se utiliza como protección un limitador suave a la salida del sistema de excitación definido en [8], para efectos del análisis. A posteriori, la ventaja de incluir este elemento se aprecia en un mayor rango de estabilidad del punto de operación del sistema. Este artículo está organizado de la siguiente manera: Inicialmente se presenta el modelo del SMIB, sobre el cual se realiza un análisis dinámico del sistema sin limitador, que incluye el cálculo de los puntos de equilibrio, el estudio de las bifurcaciones que se pueden presentar, las zonas de estabilidad y las bifurcaciones de codimensión-dos. Posteriormente, con el fin de realizar un estudio comparativo, se presenta el mismo análisis del sistema dinámico que incluye el limitador suave en el sistema de excitación. Finalmente se presentan algunas conclusiones.
Modelo del SMIB
El análisis de bifurcaciones puede ser realizado sobre un sistema de ecuaciones (1), que contiene variables X denominadas estados, los cuales varían dinámicamente, y parámetros λ, que en ciertos casos se pueden considerar que varían lentamente [2].

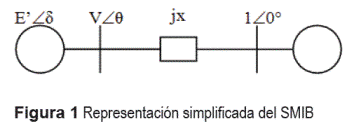
El sistema de potencia aquí analizado se modela con un conjunto de ecuaciones diferenciales no lineales de cuatro estados y dos parámetros. El sistema utilizado con un generador conectado a un barraje infinito se muestra en la figura 1. El modelo dado por las ecuaciones (2), considera tanto la dinámica del ángulo y de la tensión, así como el sistema de excitación utilizado.
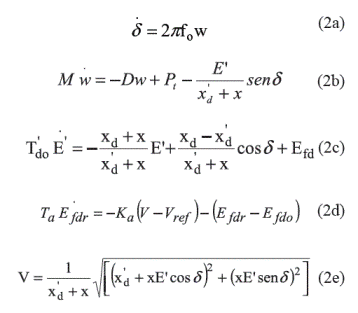
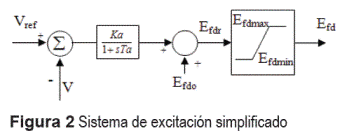
Donde δ es el ángulo del par en radianes, ω es la desviación en frecuencia de la máquina en p.u, E', Efdo y Efdr son la magnitud de la tensión antes de la reactancia transitoria, la tensión de referencia del campo y la de salida del excitador en p.u, respectivamente. Para el análisis de las bifurcaciones de codimensión-uno y -dos del sistema con y sin limitador del excitador, se consideran conocidas las constantes del excitador Ka y Ta, el momento de inercia M en segundos, la constante de tiempo transitoria T'd0, las reactancias en p.u, de línea x, eje directo xd y x›d. De igual manera se consideran constantes la tensión en el bus V y la tensión de referencia Vref. Por lo tanto, los parámetros que variarán para afectar la dinámica del sistema serán la potencia mecánica Pt (en p.u) y el coeficiente de amortiguamiento D (en p.u). La figura 2 representa el control simplificado que se realiza sobre la excitación de la máquina, donde el limitador se define en (3).
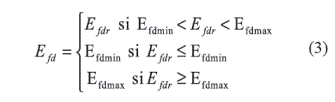
Debido a que el modelo del limitador en (3), torna al sistema de ecuaciones diferenciales en no suaves (el campo vectorial contiene zonas no diferenciables), es necesario aproximar el modelo a uno suave para realizar el estudio de bifurcaciones con herramientas de software como el toolbox para Matlab® denominado MatCont [9]. Por tanto, la función suavizada correspondiente al limitador está definida en [8], según la expresión (4), donde Efdl=5, a=0,23 y b=0,1058 :
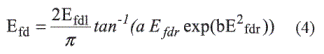
Las constantes utilizadas en el sistema se incluyen en la tabla 1.
Análisis de bifurcaciones para el SMIB sin limitador
En esta sección se analizan los efectos en la estabilidad del sistema al variar los parámetros Pt y D, cuando no se considera el limitador a la salida del excitador.
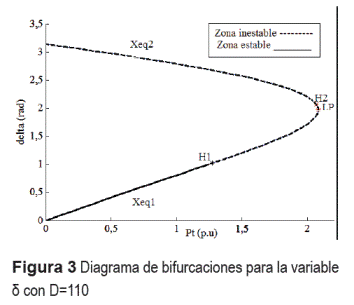
Puntos de equilibrio: Un punto de equilibrio Xeq de un sistema autónomo, como el descrito en (2), es una solución invariante del mismo que implica f(Xeq)=0. Aplicando este concepto, se tiene por inspección que el factor de amortiguamiento D no influye sobre la estructura de los puntos de equilibrio; caso contrario de la potencia Pt, puesto que Dw=0. En la figura 3, se presentan los valores del ángulo S que pertenecen a puntos de equilibrio, ante la variación de Pt.
En la figura 3 existe un valor de Pt igual a 2,08 p.u donde existe un punto de equilibrio y para valores mayores, estos ya no existen. A este valor de Pt se le conoce como bifurcación silla-nodo o limit point (LP). También existen dos bifurcaciones de Hopf, H1 y H2 que originan ciclos límite [2]. Para valores del parámetro Pt anteriores al evento LP, el sistema cuenta con dos puntos de equilibrio dados por Xeq1 (puntos inferiores de la curva) y Xeq2 (puntos superiores de la curva). Con los valores propios del sistema, se comprueba que el punto de equilibrio Xeq1 es localmente estable antes de que se presente la bifurcación H1, es decir para valores Pt < PtH1; y es localmente inestable para valores de Pt > PtH1. En contraste, el punto de equilibrio Xeq2 es siempre inestable.
La detección de bifurcaciones locales (como LP y Hopf) en el sistema, se realiza a través del seguimiento de los valores propios del Jacobiano, cuando éste último es evaluado en los puntos de equilibrio. La tabla 2 presenta los valores propios λ del sistema en los puntos de bifurcación.
De la tabla 2 se observa como característica de la bifurcación de Hopf, el cruce por cero en el eje imaginario para uno de los pares de valores propios complejos conjugados; y en la bifurcación silla- nodo, un valor propio real que se hace cero. Estos dos tipos de bifurcación corresponden a puntos de codimensión-uno [2], ya que se detectan variando sólo un parámetro del sistema.
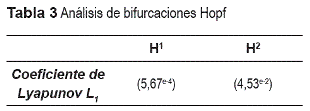
La bifurcación de Hopf, se clasifica como subcrítica o supercrítica según el tipo de estabilidad que presenten los ciclos límite que genera y puede verificarse con el primer coeficiente de Lyapunov [2]. Los coeficientes de Lyapunov son una generalización del concepto de valores propios para un punto de equilibrio y de los multiplicadores característicos para órbitas periódicas, ya que su signo provee una representación cualitativa de la dinámica del sistema. Para el sistema en estudio, se obtuvieron valores positivos (tabla 3) para el primer coeficiente de Lyapunov L1 en las bifurcaciones Hopf de la figura 3.
Por tanto, se tienen bifurcaciones Hopf subcríticas, lo cual implica que un ciclo limite inestable existe antes de la bifurcación, luego se reduce hasta que desaparece a través de la colisión con un punto de equilibrio estable en la bifurcación (ver Figura 4). Posterior a la bifurcación, el punto de equilibrio se torna inestable.
Determinación de zonas de estabilidad con el diagrama de bifurcaciones (SMIB sin limitador)
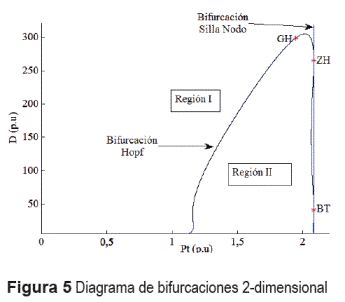
Cuando se analiza la estabilidad de un sistema, es importante determinar la influencia que ejerce la variación de sus parámetros sobre el punto de operación. Aunque existen algunas herramientas analíticas suficientemente potentes para observar dicha influencia, en muchos casos son de muy difícil aplicación. Para el sistema analizado, se realizó una continuación variando los parámetros D y Pt de las bifurcaciones Hopf y silla-nodo, halladas anteriormente, según la figura 5.
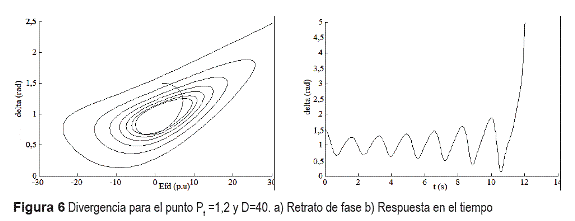
En la figura 5 se observa una línea vertical de bifurcaciones Silla-Nodo para Pt = 2,0826, lo que significa que siempre se presentará dicha bifurcación sin importar el amortiguamiento D del sistema. Para la curva de bifurcaciones Hopf, ambos parámetros Pt y D influyen. Tambien, existe un punto donde se intersecan ambas curvas, denominado de codimensión- dos de tipo Zero-Hopf (ZH) o Fold-Hopf [10], el cual se analizará más adelante. El rango utilizado para el coeficiente D es amplio, ya que en la práctica puede oscilar entre -10 p.u y 20 p.u. Sin embargo para fines académicos, se ha considerado un rango mayor con el fin de ilustrar la presencia de bifurcaciones de codimensión-dos, las cuales enriquecen notablemente el comportamiento dinámico del sistema. A continuación se representa el análisis de la estabilidad de algunos puntos ubicados en las regiones I y II de la figura 5, delimitadas por la curva de bifurcaciones Hopf. Para cada punto se presenta el retrato de fase y su representación temporal. En la figura 6 se observa inestabilidad.
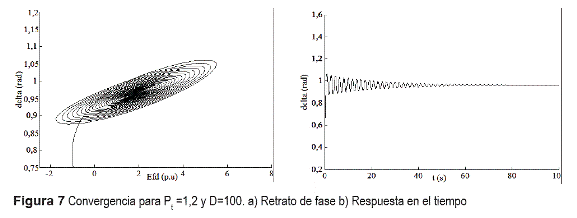
Para un valor de D más alto, el comportamiento del sistema es estable, según la figura 7.
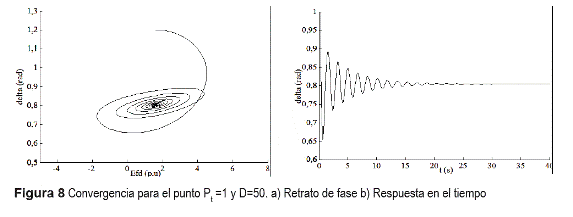
De igual manera, la estabilidad se mantiene para un valor menor de Pt y D (Figura 8).
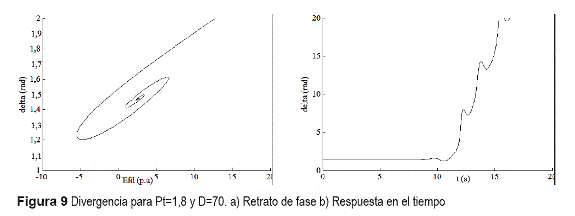
El sistema pierde estabilidad para el punto definido en la figura 9.
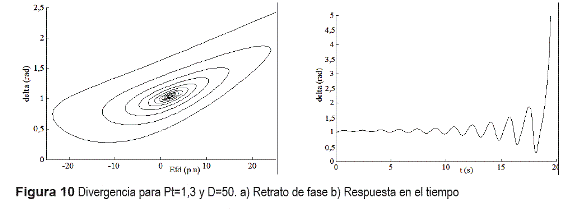
Igual comportamiento se presenta para el punto analizado (Pt=1,3 y D=50), según la Figura 10.
Como se comprueba de las anteriores figuras, la curva de bifurcaciones Hopf divide el espacio de parámetros en dos regiones: I correspondiente a puntos de equilibrio estables según las figuras 7 y 8; y II correspondiente a puntos inestables según las figuras 6, 9 y 10.
Análisis de los puntos de codimensión-dos:
Los puntos correspondientes a bifurcaciones de codimensión-dos se pueden presentar en un sistema debido al aumento de la dimensión de la variedad centro, o a la falla de algunas de las condiciones de no degeneración [10]. A partir de la figura 5, las bifurcaciones de codimensión-dos que se presentan en el sistema son del tipo: Hopf generalizada (GH), Bogdanov-Takens (BT) y Zero-Hopf (ZH) [10]. En este artículo se analizará esta última, debido a que es la que ofrece mayor cantidad de fenómenos dinámicos a su alrededor, a partir de los coeficientes obtenidos.
- Bifurcación Zero-Hopf (ZH): En este tipo de punto de codimensión-dos, el Jacobiano correspondiente al punto de equilibrio tendrá un valor propio igual a cero y un par conjugado de valores propios imaginarios puros. En la tabla 4 se presentan las características de dicho punto.
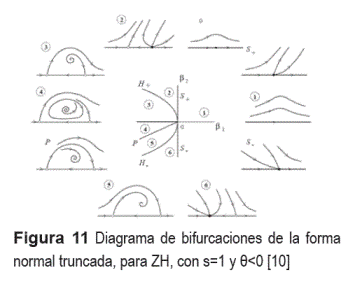
De acuerdo con Kuznetsov [10], cuando se verifica s=1 y θ<0, se tiene que la forma normal truncada contiene, alrededor del punto ZH, tanto bifurcaciones de Hopf subcríticas como supercríticas; y bifurcaciones Neimark-Sacker, que producen órbitas cuasiperiódicas (también denominadas toros). En la figura 11, se ilustra el diagrama de bifurcaciones correspondiente [10].
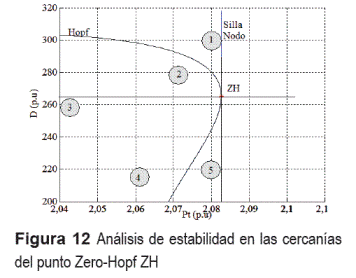
Según lo expuesto, solo las bifurcaciones locales de la forma normal truncada se mantienen para el sistema original en estudio. La curva P en la figura 11 no existe en el sistema original, aunque en sus cercanías se tiene un conjunto de bifurcaciones globales (órbitas homoclínicas y tangencias heteroclínicas), así como bifurcaciones de ciclos límite de periodos altos (producidos en bifurcaciones silla-nodo y doblamiento de período) que causan comportamientos caóticos. Para analizar los fenómenos dinámicos cerca del punto ZH, se establecen cinco regiones (1 a 5 en la figura 12), en las cuales se simulan las trayectorias a partir de diferentes puntos de operación.
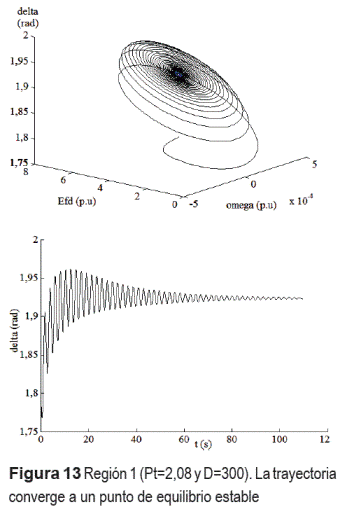
a) Región 1: En esta región se presenta un punto de equilibrio estable (Figura 13) y otro inestable.
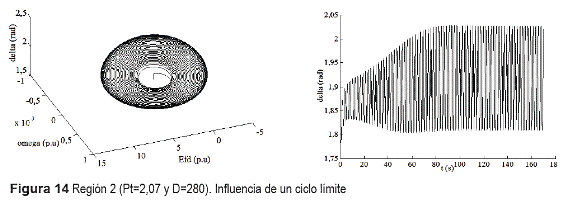
b) Región 2: Oscilaciones sostenidas debido a la cercanía con un ciclo límite estable (figura 14).
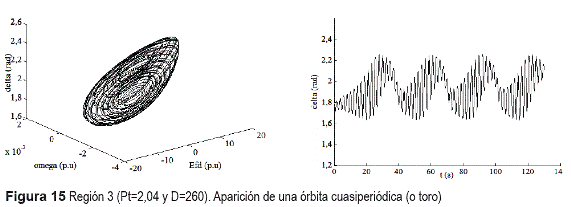
c) Región 3: Con la disminución de D en esta zona, se observa que la trayectoria se mueve sobre una superficie toroidal, correspondiendo a la señal en el tiempo de la figura 15.
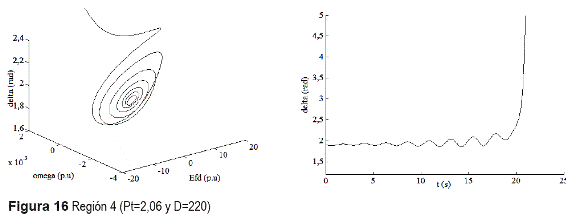
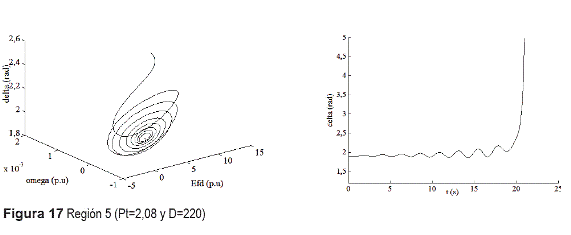
d) Regiones 4 y 5: Ha desaparecido el toro y no hay puntos de equilibrio estables (Figuras 16 y 17).
Este comportamiento coincide con [10] para el caso s=1 y θ<0. Como E0 es negativo (tabla 4), las direcciones de los campos vectoriales en la figura 11 deben ser revertidas. Así, la región 1 de la figura 12 corresponde con la región 2 de la figura 11, y las regiones 2, 3, 4 y 5 de la figura 12 corresponden con las regiones 3, 4, 5 y 6 de la figura 11, respectivamente. Después de la destrucción del toro, en las regiones 4 y 5 de la figura 12, sólo permanecen puntos de equilibrio o ciclos límite inestables, y por eso divergen las trayectorias mostradas en la figuras 16 y 17.
De acuerdo con los resultados obtenidos, es importante conocer los límites de operación del sistema para establecer adecuadamente sus márgenes de estabilidad. Sin embargo, esto no es suficiente en sistemas tan complejos como los eléctricos, pues su comportamiento dinámico y alta dependencia del punto inicial de operación, causa respuestas estables o inestables, ante una misma perturbación. Por tanto, la estabilidad de un sistema no debe restringirse solamente a la interpretación y análisis de un diagrama de bifurcaciones como el de la figura 3, sino que es necesario caracterizar el entorno de los puntos definidos como estables, con el fin de definir las posibles dinámicas bifurcacionales que los puedan afectar ante la variación de sus parámetros.
Análisis de bifurcaciones para el SMIB con limitador
En esta sección se analiza el comportamiento del SMIB con el limitador dado por la ecuación (4).
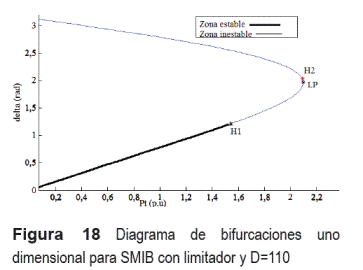
Puntos de equilibrio: Con el limitador suave en la excitación, se obtiene la figura 18.
En la figura 18 se observa un corrimiento a la derecha del punto H1 y el consecuente aumento en el rango de estabilidad para la variable 8, respecto a la figura 3. En la tabla 5 se presentan los datos correspondientes a las bifurcaciones presentadas. Con L1 de H2(-), se tiene una bifurcación supercrítica generadora de ciclos límites estables [2].
Determinación de zonas de estabilidad con el diagrama de bifurcaciones (SMIB con limitador)
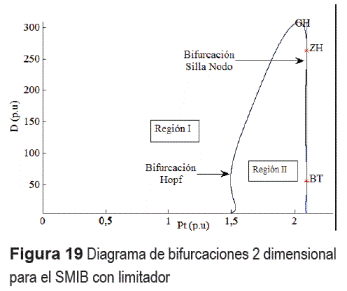
La continuación de las curvas de bifurcaciones Hopf y silla-nodo obtenidas en el sistema con el limitador suave dado en la ecuación (4), se obtiene la figura 19, que presenta el mismo tipo de puntos de codimensión-dos del modelo sin limitador, aunque algunos de ellos cambian de posición.
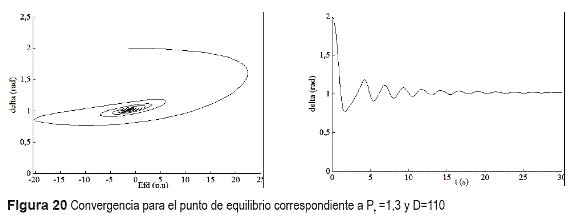
Se observa que la región II disminuye en comparación con la de la figura 5, consiguiendo con ello aumentar la región estable. Con el fin de verificar esto, se ilustra a continuación el plano de fase y la evolución temporal de δ para puntos de equilibrio, que en el modelo sin limitador eran inestables, pero que ahora no lo son. En la figura 20 se comprueba la anterior aseveración.
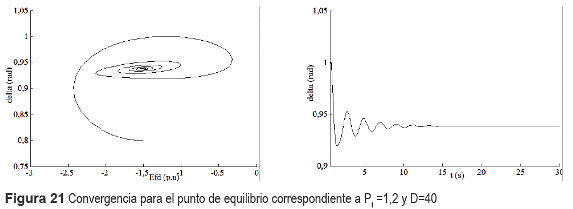
De igual forma el punto correspondiente a Pt=1,2 y D=40 es estable según figura 21.
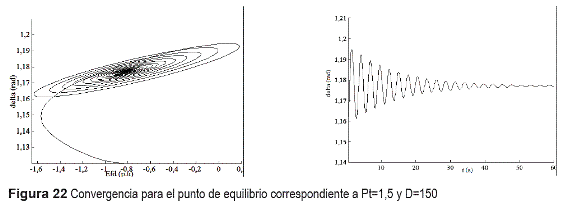
En la figura 22 se aprecia el amortiguamiento de la señal δ para un valor mayor de D.
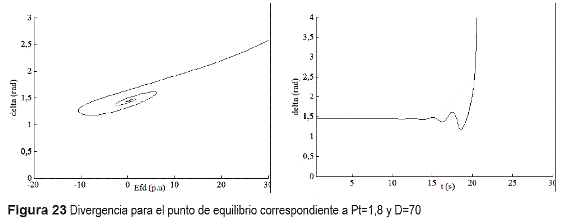
En cambio para el punto Pt=1,8 y D=70, el sistema pierde estabilidad, según la figura 23.
Análisis de puntos de codimensión-dos
Con el fin de realizar un estudio comparativo entre las respuestas dadas por el sistema SMIB sin y con limitador, también se lleva a cabo el análisis de la bifurcación ZH para este último.
- Punto Zero-Hopf: Las características del punto ZH se presentan en la tabla 6.
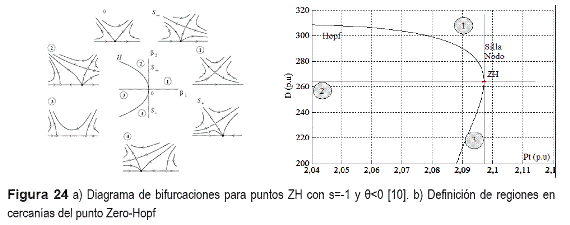
De acuerdo con [10], para s=-1 y θ<0 en la forma normal truncada se obtienen bifurcaciones Hopf subcríticas y ninguna tipo Neimark-Sacker que den lugar a órbitas cuasiperiódicas, como en la figura 24a. Para efectos de análisis, se divide la zona cercana a ZH en 3 regiones (figura 24b).
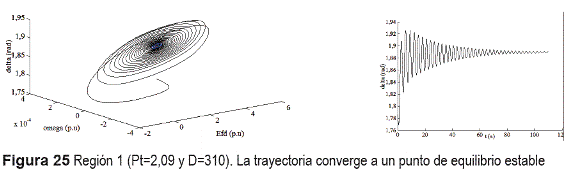
a) Región 1: En esta región el punto de equilibrio es estable como es demostrado en la figura 25.
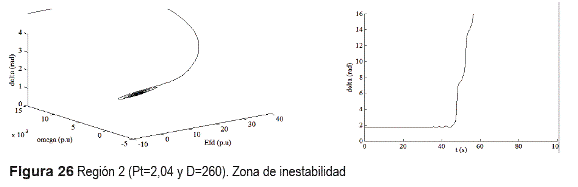
b) Región 2: En esta región el punto de equilibrio es inestable, como lo demuestra la figura 26.
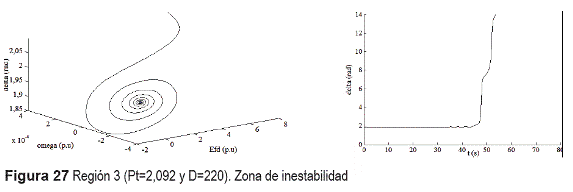
c) Región 3: Según la figura 27, en esta región se pierde estabilidad.
Al igual que en el caso del sistema sin limitador, el comportamiento bifurcacional descrito en esta sección coincide plenamente con lo establecido en [10] para el caso s=-1 y θ<0. Con signo negativo de E0 (ver tabla 6), las direcciones de los campos vectoriales en la figura 24-a, deben ser revertidas. Así, la región 1 de la figura 24-b corresponde con la región 2 de la figura 24-a, y las regiones 2 y 3 de la figura 24-b con 3 y 4 de la figura 24-a, respectivamente. Después de la bifurcación de Hopf presentada entre las regiones 1 y 2 de la figura 24-b, solo permanecen puntos de equilibrio o ciclos límite inestables, y por eso divergen las trayectorias en las figuras 26 y 27.
Conclusiones
Se ha presentado un análisis detallado de la estabilidad de un sistema de potencia simple, desde el punto de vista de magnitud y número de componentes, pero bastante representativo en cuanto su dinámica, permitiendo con ello revisar la influencia que tiene la utilización de un limitador suave en la excitación, al extender ligeramente la zona de estabilidad. Aunque en la práctica no es común la utilización de dicho limitador en los sistemas de control, el ejercicio realizado en el artículo permite observar, mediante el análisis de puntos de codimensión- dos como la Zero-Hopf, que cerca del límite del colapso de tensión, aparecen fenómenos de bifurcación Hopf que llevan a la existencia de, o bien puntos de equilibrio y ciclos límite desestabilizadores (SMIB con limitador), u oscilaciones cuasiperiódicas o caóticas (SMIB sin limitador).
Referencias
1. IEEE/PES Power System Stability Subcommittee. "Voltage stability assessment. Procedures and guides". 2001. http://www.power.uwaterloo.ca. Consultada el 20 de mayo de 2010. [ Links ]
2. R. Seydel. Practical bifurcation and stability analysis: from equilibrium to chaos. 3a. ed. Ed. Springer. New York. 2009. pp. 303-483. [ Links ]
3. V. Venkatasubramanian, W. Ji. "Dynamics of a minimal power system: Invariant Tori and Quasi- Periodic Motions". IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. Vol. 42. 1995. pp. 981-1000. [ Links ]
4. E. H. Abed, H. O. Wang, J. C. Alexander, A. M. A. Hamdan, H. C. Lee. "Dynamic bifurcations in a power system model exhibiting voltage collapse". International Journal Bifurcations and Chaos. Vol. 3. 1993. pp. 1169-1176. [ Links ]
5. V. Venkatasubramanian, W. Ji. "Hard-limit induced chaos in a fundamental power system model". Electrical Power & Energy Systems. Vol. 18. 1996. pp. 279-295. [ Links ]
6. G. Revel, A. León, D. Alonso, J. Moiola. "Bifurcation Analysis on a Multimachine Power System Model". IEEE Transactions on Circuits and Systems. Vol. 57. 2010. pp. 937-949. [ Links ]
7. C. J. Budd, J. P. Wilson. "Bogdanov-Takens bifurcation points and Sil'nikov homoclinicity in a simple power-system model of voltage collapse". IEEE Transactions on Circuits and Systems - I. Fundamental Theory Applications. Vol. 49. 2002. pp. 575-590. [ Links ]
8. R. G. Kavasseri, K. R. Padiyar. "Analysis of bifurcations in a power system model with excitation limits". International Journal Bifurcation and Chaos. Vol. 11. 2001. pp. 2509-2516. [ Links ]
9. A. Dhooge, W. Govaerts, Y. Kuznetsov "MATCONT and CL-MATCONT Continuation Toolboxes in MATLAB". 2006. http://www.ricam.oeaw.ac.at/Teaching/MathModelBioSciences/EX3/MATCONTmanual.pdf. Consultada el 1 de abril de 2010. [ Links ]
10. Y. Kuznetsov. Elements of Applied Bifurcation Theory. 3a. ed. Ed. Springer-Verlag. New York. 2004. pp. 330-348. [ Links ]
(Recibido el 26 de mayo de 2010. Aceptado el 10 de marzo de 2011)
*Autor de correspondencia: teléfono/fax: + 57 + 6 + 313 71 22, correo electrónico: saperez@utp.edu.co. (S. Pérez)