Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.60 Medellín Oct./Dec. 2011
Comparative study for chaotic behaviour in fire fighting robot
Estudio comparativo de comportamiento caótico en un robot de combate a incendios
Magda Judith Morales Tavera1*, Omar Lengerke2, Max Suell Dutra1
1Mechatronics Systems & Robotics Research Group, Federal University of Rio de Janeiro, COPPE/UFRJ. Postal Box 68.503, CEP 21.945-970. Rio de Janeiro. Brasil.
2Autonomous University of Bucaramanga - UNAB. Calle 48 N.° 39-234, Bucaramanga, Colombia.
Abstract
The fire fighting monitoring work is a case study where the chaotic control could minimize human, material and environmental injuries. In this paper, we proposed a chaotic control for a mobile robot, in order to do a further inspection in regular spaces, moving it through time with non determinate trajectories. A chaotic nature in the mobile vehicle is added, putting together kinematics with non linear equations such as Arnold and Lorenz, in the same system.
Keywords: Chaos, fire fighting, mobile robots, non linear.
Resumen
El trabajo de supervisión de incendios es un caso de estudio, donde el control caótico podría minimizar las lesiones en humanos, materiales y ambientales. En este artículo se propone un control caótico para un robot móvil, con el fin de hacer una nueva inspección en espacios regulares, desplazándolo a través de trayectorias no determinadas. Una naturaleza caótica en el robot, es adicionada, integrando la cinemática con las ecuaciones no lineales de Arnold y Lorenz, en el mismo sistema.
Palabras clave: Caos, combate de incêndios, robótica móvil, no lineal.
Introduction
The applications of the robotic systems are diverse; these include the substitution of humans in repetitious and very sensitive to error works, also, assistance for physically handicapped person, or vigilance and operation in dangerous environments. The ambition of the society is the substitution of the human with robotics system in activities that put in risk the human integrity, operations which the human ability are not able to work in optimal conditions. A fire fighting monitoring work is a case study where the chaotic control could minimize human, material and ambient injuries in the moment of realize inspection on determined environments. For example, the fire fighters are continuously exposed to common dangers, in many cases, their lives are in risk and eventually deceases are in registering. Events like building fallings or concentration of smoke in small places are examples of dangerous situations that involve human losses. Consequently, the solution is to keep a safe distance using remote control (Teleoperation) or autonomous vehicles.
The main cause of life and properties losses around the world is the fire [1]. The fire could destroy completely installations, the work resources, indeed, could be reduced, affecting the economy of countries and his population. The fire fighting and rescue activities are recognized as risky missions, while they are extinguished fire and rescuing people. In contrast, a robot could have an autonomous operation being controlled from a remote distance in order to do secure activities without put in risk the fire fighting life. In other works, the robots could reduce the necessity of fire fighters exposition in some situations, decreasing the dangerous that they are exposed. The first life that the fire fighters have to rescue is their proper life [2].
Many ideas of autonomous guided robots have been developed, all following defined trajectories, but are unnecessary when the global idea is to explore an uncertain zone [3, 4]. One solution is showed by [5]; they added a chaotic behavior in a mobile robot trajectory, making it moving randomly in the space, helping in a better way in the explorations tasks.
The chaos characterizes is one of the most mysterious and rich behaviors of nonlinear dynamical systems [6]. Many research efforts have been realized to establish the mathematical theory behind chaos. The applications of chaos are also being studied and included, for example, in controlling chaos and chaotic neural networks. This paper follows a method to impart chaotic behavior to a mobile robot. This is achieved by designing a controller which ensures chaotic motion [5].
Chaos phenomena have been useful integrated in diverse applications, since XIX century, with Poincare and Lyapunov studies in the topological structure in the phase space of dynamical trajectories. Some researches began the formation of theories that allow the implementation of dynamics behaviors in diverse areas such as, communications [7-9], genetic Algorithms [10], communications security with chaotic pulse generation [11], among others.
Numerous dynamical systems achieve a chaotic behavior if their controller parameters are modulated to certain values. In a physical outlook, when a natural phenomenal are exposed to specifically conditions [12]. Researchers formulated an idea for add chaotic behavior in a stable system, they connected two systems, one as a non linear driven system, responsible by generation of the control signal, from which the second one (the response system) is steered, achieving non linear behavior also [13].
The purpose in this paper, is position a fire fighting robot as a response system, and analyzes his behavior with different non linear systems as drivers. In the next section is analyzed the fire fighting robot model, in the section 3 and 4 is added an brief review of the non linear systems used in the experiments, in section 5 the integration of the different systems through simulations, and finally in section 6, is registered the conclusions of this work and future researches.
Fire fighting robot
As every process, the fire could exist in diverse forms; all involve a chemical reaction between different kinds of combustible, oxygen and air. Correctly used, the fire is a great benefice as an energy and heat source in industry and home necessities, but, not controlled, it could generated strong material harm and human suffering. Because of that, could be said that a fire's dynamic study is essential for the Fire Protecting Engineers as a chemical study is for a Chemical Engineer [14].
Robotics is a high success of industry and manufacturing in the world, for example the robotic arms that could move with high speed and realize with precision repetitive works, but they have a fundamental disadvantage: the reduced movement. Nevertheless, a mobile robot could move in a determinate ambient realizing the programmed work in the certain place. In a hazard and dangerous environment, mobile robots supply the necessity of locomotion mechanism, making that teleoperated or autonomous mechanism earn great popularity.
For the proposal work, a wheel robot configuration is adopted; the wheels are the locomotion mechanism more popular in mobile robotic, because they could reach much efficiency with really simplex mechanicals implementations [15]. Normally, the equilibrium is not a research problem in wheeled mobile robots projects, because the wheels robots are planned to be on permanent contact with the soil, all time. For this reason three wheels are enough for guarantee a stable equilibrium. Instead of worrying about the equilibrium, the researches of wheeled mobile robot are focused in tractions and stability problems, maneuver and control. The principal purpose of this research is the control applied on the proposed robot, in this section is studied the robots kinematics and subsequently applied into the controller.
Kinematics is the study of the mechanism behavior, in mobile robots is necessary understand the mechanical behavior in order to analyze the implementation of control software. The mobile robot model could be like a rigid body and wheels [16, 17]. As the mathematical model of mobile robots, assume a two-wheeled mobile robot as shown in figure 1.
Let linear velocity of the robot 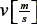 and angular velocity
and angular velocity 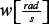 are inputs of the system. The state equation of the mobile robot is written in equation (1).
are inputs of the system. The state equation of the mobile robot is written in equation (1).
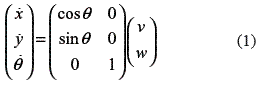
Where (x[m], y [m]) is the position robot and θ[rad] is the angle of the robot.
The arnold equation
In order to generate chaotic motions of the mobile robot, one of the chaotic systems utilized the Arnold equation, which is written in equation (2).
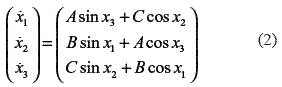
Where A, B, and C are constants. The Arnold equation describes a steady solution to the three-dimensional (3-D) Euler equation (Equation (3) and Equation (4)).
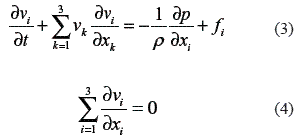
The Equation (3) and Equation (4) expresses the behaviors of no compressive perfect fluids on a 3-D torus space. (x1, x2, x3) and (v1, v2, v3) denote the position and velocity of a particle and p, (f1, f2, f3) and ρ denote the pressure, external force, and density, respectively. It is known that Arnold equation shows periodic motion when one of the constants, for example C, is 0 or smaller, and shows chaotic motion when C is superior.
Behavior analysis
With x2 = 0 the system to analyze is in equation (5).
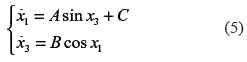
Matching with zero both equations find a set of infinite equilibrium points 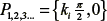 where ki is an odd number, and
where ki is an odd number, and 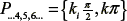 where k is an integer number. In order to analyze the behavior of the equilibrium points, the Jacobian are implemented on equation (6).
where k is an integer number. In order to analyze the behavior of the equilibrium points, the Jacobian are implemented on equation (6).
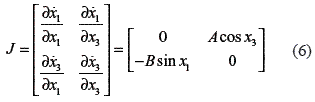
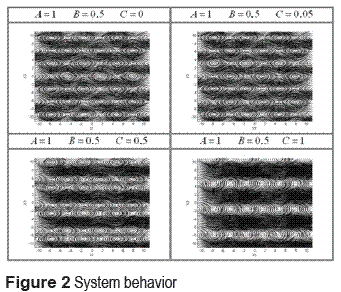
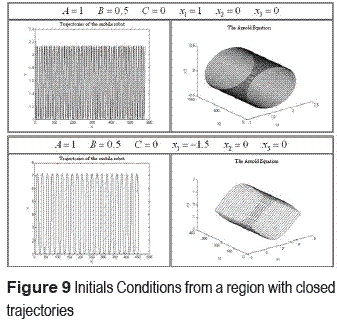
Where the eigen values of the square and real matrix are the solutions of the characteristic polynomial 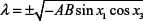 that define the behavior of the system for different values A and B, such behavior could be seen in the figure 2. When C = 0, is observed that topological transitivity does not emerge, since the trajectories in the Poincaré section are closed. When |C| exceeds a certain small number and gets larger, there are grown regions in which closed trajectories disappear and scattered discrete points appear. The regions characterize chaos and behavior. Since Arnold equation is a conservative system, is an important feature that discrete trajectory of a point initially started in such a region remains there and is never attracted by the closed trajectories outside region.
that define the behavior of the system for different values A and B, such behavior could be seen in the figure 2. When C = 0, is observed that topological transitivity does not emerge, since the trajectories in the Poincaré section are closed. When |C| exceeds a certain small number and gets larger, there are grown regions in which closed trajectories disappear and scattered discrete points appear. The regions characterize chaos and behavior. Since Arnold equation is a conservative system, is an important feature that discrete trajectory of a point initially started in such a region remains there and is never attracted by the closed trajectories outside region.
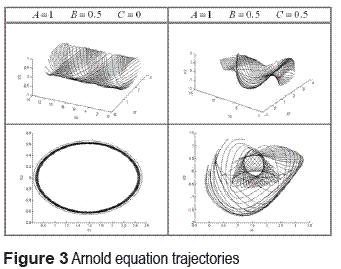
In the figure 3 are shown Arnolds equations trajectories for different values of the C parameter.
The lyapunov exponent
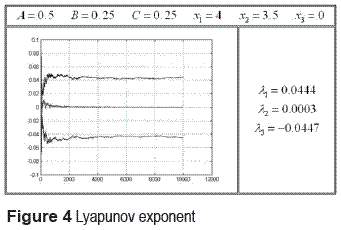
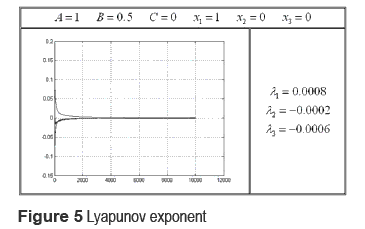
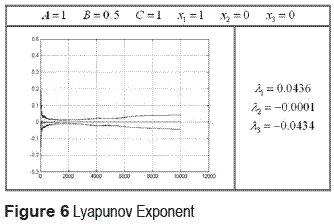
The Lyapunov exponent is used as a measure of the sensitive dependence on initial conditions, that is, one of two characteristics of chaotic behavior. There are n Lyapunov exponents in n-dimensional state space and the system is concluded to have the sensitive dependence on initial conditions when the maximum Lyapunov exponent is positive. Is calculated the Lyapunov exponent of Arnold equation for different coefficients and initial states (figure 4, figure 5 and figure 6).
Since the maximum exponent is positive, Arnold equation has sensitive dependence on initial conditions. In case of Arnold flow, the sum of Lyapunov exponents λ1 + λ2 + λ3 equals zero, it means that volume in the state space is conserved. This results is the fact that a trajectory which started from a chaotic region will not be attracted into attractors like limit cycles. The total of the computed Lyapunov exponents became slightly larger than zero, which is due to the numerical computation error.
The lorenz equation
The Lorenz equations are a well known non linear equations system, named after and created by the meteorologist Lorenz, this model was made as a modification of Navier-Strokes equation system (Equation (7)).
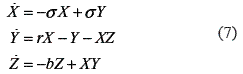
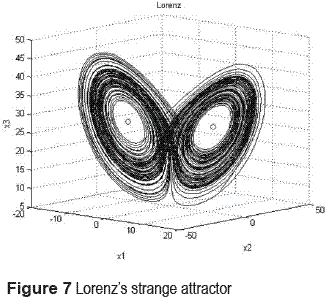
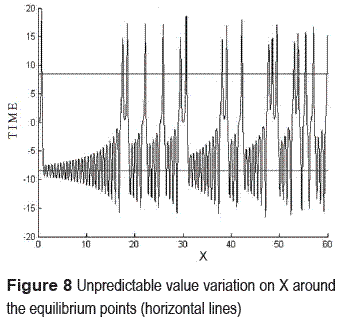
The control parameters are, the Prandalt number σ, the Raileigh number r, and the geometric measure b. The system is non conservative, it means, that along the time energy loss, generating a variation this form, therefore, the apparition of strange attractors (figure 7), and the system assume a chaotically behavior, making constants changes on its values, almost unpredictable around the equilibrium points (figure 8). These changes are limited by the boundary of attractor, its means, which cannot reach another value out of there.
The parametric values required to input a chaotically behavior on the Lorenz System are: σ = 10, r = 28, b = 3/8. Lorenz is also sensitively depend on initial conditions with these values, which mean, a variation of trajectories for different values, however the existence of the strange attractor limits the expansion of trajectories, being all globally apparent.
Integrated system
Arnold equation integration
In order to integrate the Arnold equation into the controller of the mobile robot, is defined and used state variables (equation (8)).
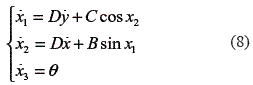
where B, C and D are constants. Substituting on the equation (8) the equation of the mobile robot is defined in equation (9).
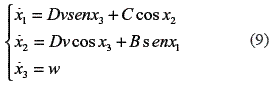
The design the inputs is shows in equation (10).
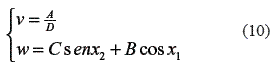
Consequently, the state equation of the mobile robot becomes in equation (11).
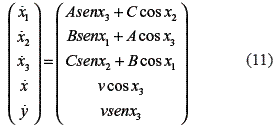
The equation (11) includes the Arnold equation. The Arnold equation behaves chaotically or not, depending of the initial states, we choose the ones of the Arnold equation such that the trajectory should became chaotically. It is guaranteed that a chaotic orbit of the Arnold equation is not attracted to a limit cycle or a quasi-periodic orbit. The whole states evolve in a 5-D space according to equation (11), which includes a 3-D subspace of the Arnold flow. The state evolution in the 2-D complementary space is highly coupled with the one in the 3-D subspace as seen in equation (11). The coupling is physically interpreted by the fact that the mobile robot moves with a constant velocity and being steered by the third variable of the Arnold equation.
The inputs to mobile robot become continuous since the Arnold equation is a continuous system. Though the Rössler equation, the Lorenz equation, and so on, are well known as low-dimensional continuous chaotic systems. The Arnold equation has some advantages as follows: (i) the structures of the Arnold equation and mobile robot equation are similar, (ii) it is easy to deal with it because the state variables x1, x2, and x3 are limited within a 3-D torus space, (iii) the range of the input w becomes -(|B|+ |C|) ≤ w ≤ (|B|+ |C|) and suitable for a robot input, and (iv) the maximums of | 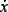 1|, |
1|, | 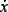 2|, |
2|, | 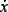 3| are determined by parameters A, B,and C.
3| are determined by parameters A, B,and C.
The figure 9 and figure 10 show examples of motions of the mobile robot with the proposed controller, obtained by numerical simulation. Some initials conditions were chosen from a region where the Poincaré section forms no closed trajectory (figure 10). Is observed that the robot motion is unpredictable and sensitively dependent on initial conditions.
Lorenz equation integration
In the same way that was done with the Arnold equation, is coupled the two Lorenz equations with the robot mobile system, the parameter Z will be angular position (θ), and therefore the angular velocity 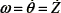 is consider in equation (12).
is consider in equation (12).

Creating in this form one 5-D dimension equation systems (equation (13)).
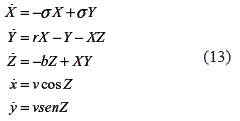
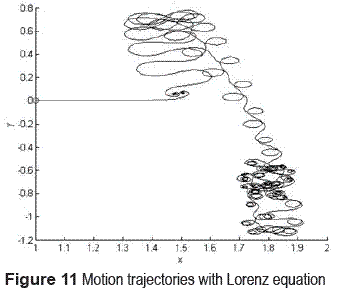
In the same method that the first example, in equation (13) the first 3-D system correspond the Lorenz equations, and it will drive the 2-D sub system correspond to mobile robot. All the simulations was realized with the control parameter configurations that leads to Lorenz to a chaotically behavior. The figure 11 shows a simulation of the mobile robot behavior with a constant velocity v = 1 m/s, initial conditions for robot mobile of (x, y) = (1.0) and duration 20 time units.
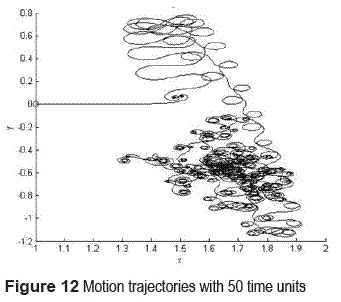
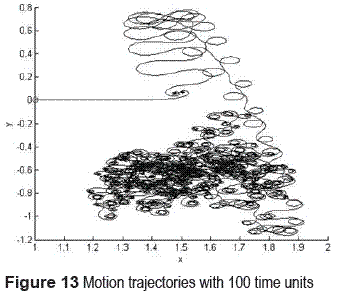
Increasing the time the robot mobile path creases in the space, covering more area. The figures 12 and 13, shows that the distance an trajectory path of the robot increasing directly with the time, however, the existence of the strange attractor in the system, makes that path exist only into a specifically area, all movements out of there are restricted.
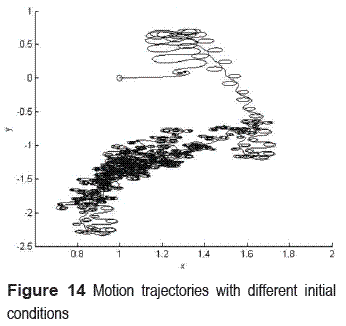
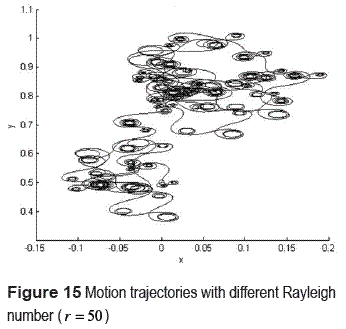
The only way for make a different path is changing the initial conditions in the Lorenz system (figure 14), or changing the value of the Rayleigh number r (figure 15) but, in this case is important to make sure that the Lorenz System still having a chaotically behavior like seen in the figure 7.
Comparison
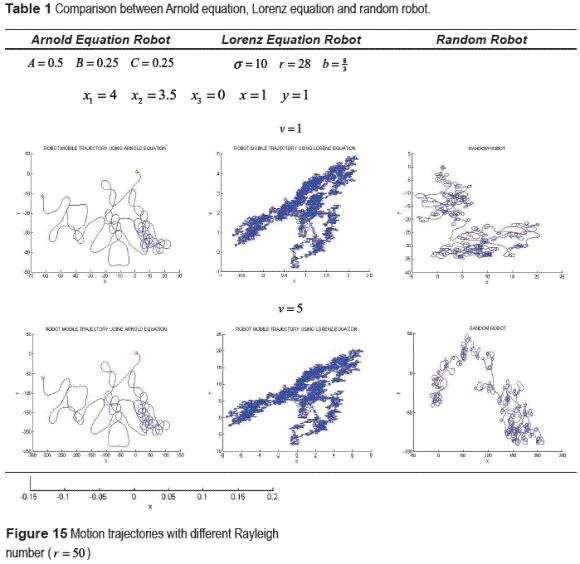
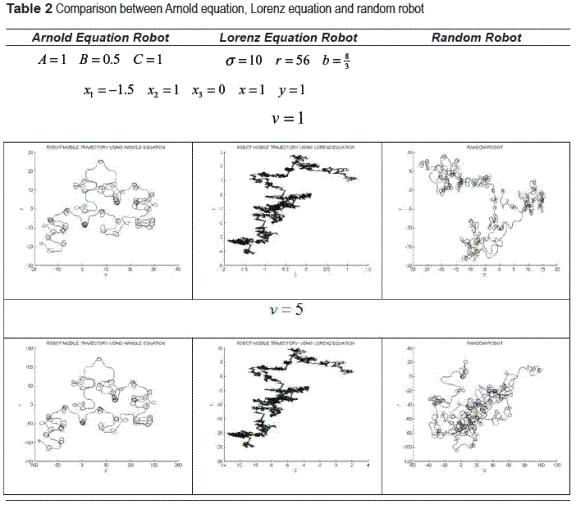
In this section is realized a comparison between the proposal systems and a robot droved with a random behavior. The random steering generates random inputs to the robot every two seconds, the system moves according with the generated input, and changes when a new input is generated. In the table 1 and table 2 compare the case study, using different parameters, initial conditions and velocities in each case.
The trajectory realized by the Lorenz robot is the most detailed making redundant moves inside its work area, random robot an Arnold robot cover a large sector of area as show the limits on the graphics, but is interesting to note that Arnold made a superior exploration than the random one in the same space of time.
In tables 1 and 2 is observed that the trajectories formed with Arnold and Lorenz equations not change with the variation of their velocities, there only expands its workspace, the sensibility to the initial conditions is the cause of this change on their behavior. The random robot presents a different behavior for each experiment due to its uncertain nature. The experiences demonstrate that the random robot can't make and bigger exploration than the Arnold one, also that the Lorenz robot path always shows to be restricted on a workspace and its covertures area is lesser.
Conclusiones
In this paper, we proposed the implementation of chaotic behavior on a fire fighting robot, which implies a mobile robot with a controller that guarantees a chaotic motion. The Arnold and the Lorenz equations, which are known to show chaotic behavior, were adopted as the chaotic dynamics to be integrated into the mobile robot; the behaviors of these equations on the system were analyzed. We designed the controller explained that the total dynamics of the mobile robot is characterized by the Arnold and the Lorenz equations.
This kind of chaotic control could explore a dangerous space in order to find ignitions sources or make a map of the location's current state, in this way we can find "the obstacles" that could exists. All this implementation is for futures works. Using this, the fire fighting corps could know what the best path is for rescuing victims, do cleaning and disaster evaluation.
One importance of this kind of inspections is rescue life of people involved in this work, we must to make sure that the minimal risks are taken, the implementation of chaotic control is an exceptional suggest for the fire fighting robot area.
Comparing between the studied systems is possible to conclude that the robot that realizes the major special coverage is the Arnold one. One of the advantages of Arnold robot with the random one, is that always execute its move in the same way, realizing the same path. The random robot variation not allow to the system to make the same performance between experiences, making different results between experiences, but its coverage area is always lesser than the Arnold one. The next step on this work is reduce the workspace into one specific area with, the reduction of the area allows to put the robot in a particular ambient, where could exists obstacles and sectors that have to be avoided during the movement.
Referencias
1. M. Y. H. Bangash, T. Bangash. "Explosion-Resistant Buildings". Ed. Springer Verlag. Londres. 2006. pp. 46-52. [ Links ]
2. H. Amano. "Present Status and Problems of Fire Fighting Robots". Proceedings of the 41st SICE Annual Conference SICE 2002. Vol. 2. 2002. pp. 880-885. [ Links ]
3. Y. Kanayama, Y. Kimura, F. Miyazaki, T. Noguchi. "A Stable Tracking Control Method for an Autonomus Mobile Robot". Proceedings of the 1990 IEEE International Conference on Robotics and Automation. Vol. 2. 1990. pp. 384-389. [ Links ]
4. V. Muñoz, A. Ollero, M. Prado, A. Simón. "Mobile Robot Trajectory Planning with Dynamics and Kinematics Constraints". Proceedings of the IEEE International Conference on Robotics and Automation. Vol. 4. 1994. pp. 2802-2807. [ Links ]
5. Y Nakamura, A. Sekiguchi. "The Chaotic Móbile Robot". IEEE Transactions on Robotics and Automation. Vol.17. 2001. pp. 898-904. [ Links ]
6. M. Savi. "Dinámica Nao-Linear e Caos". Ed. e-paper. Rio de Janeiro. Brasil. 2006. pp. 75-97. [ Links ]
7. J. M. T. Thompson, H. B. Stewart. Nonlinear Dynamics and Chaos. Ed. John Whiley and Sons. Great Britain. 1996. pp. 291-347. [ Links ]
8. A. Astari, G. Thomas, W. Kinsner. "Sufficient Conditions for Chaotic Maps to Yield Chaotic Behavior after FM". IEEE Transactions on Aerospace and Electronic Systems. Vol. 44. 2008. pp. 1240-1248. [ Links ]
9. K. M. Cuorno, A. V. Oppenheim, S. H. Strogatz. "Synchronization of Lorenz-Based Chaotic Circuits with Applications to Communications". IEEE Transactions on Circuits and Systems II. Analog and Digital Signal Processing. Vol. 40. 1993. pp. 626-633. [ Links ]
10. J. Determan, J. A. Foster. "Using Chaos in Genetic Algorithms". Proceedings 1999 Congress on Evolutionary Computation CEC 99. Vol. 3. 1999. pp. 2094-2101. [ Links ]
11. Y. Wang, L. Wang, S. YU, L. Zhang, D. Yan, Y. Li. Method of Chaotic Pulse Sequence Produced by Continuous Chaotic System. 9th International Conference on Proceedings Signal Processing. ICSP 2008. IEEE Conferences. 2008. pp. 1892-1895. [ Links ]
12. J. A. Maldonado, J. A Hernandez. Chaos Theory Applied to Communications. Part I: Chaos Generators. "Fourth Congress of Electronics, Robotics, and Automotive Mechanics, IEEE Computer Society". Morelos. México. 2007. pp. 50-55. [ Links ]
13. L. M. Pecora, T. L. Carroll. "Driving systems with chaotic signals". The American Physical Society. Vol. 44. 1991. pp. 2374-2384. [ Links ]
14. D. Drysdale. An Introduction to Fire Dynamics. 2a. ed. Ed. Jhon Wiley & Sons. Edinburgh. UK. 1999. pp. 1-29. [ Links ]
15. J. Jones, A. Flynn, B. Seiger. Mobile Robots, Inspiration to implementation. 2a. ed. Ed. AK Peters. USA. 1993. pp. 11-37. [ Links ]
16. J. C. Alexander, J. H. Maddocks. "On the Kinenatics of Wheeled Mobile Robots". International Journal Robot Vehicles. Vol. 8. 1989. pp. 15-27. [ Links ]
17. O. Lengerke, M. S. Dutra, F. M. G. França, M. J. M. Tavera. "Automated Guided Vehicles (AGV): Searching a Path in the Flexible Manufacturing Systems". Journal of Konbin. Vol. 8. 2008. pp. 113--124. [ Links ]
(Recibido el 7 de abril de 2010. Aceptado el 20 de junio de 2011)
*Autor de correspondencia: teléfono: + 55 + 21 + 256 277 64, fax: + 55 + 21 + 256 283 83, correo electrónico: mjmtavera@ufrj.br. (M. Morales)