Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.61 Medellín Dec. 2011
ARTÍCULO ORIGINAL
Implementación de un sistema de control activo para disminuir las vibraciones producidas por personas en una tribuna
An active control system for reducing crowd induced vibrations in a grandstand
Diego Fernando Hernández, Daniel Gómez Pizano*, Peter Thomson
Grupo de Investigación en Ingeniería Sísmica, Ingeniería Eólica y Estructuras Inteligentes, G–7. Escuela de Ingeniería Civil y Geomática. Universidad del Valle. Calle 13 N° 100–00, Edificio 350, Ciudad Universitaria Meléndez. Cali, Colombia.
*Autor de correspondencia: teléfono: + 57 + 2 + 339 24 20, fax: + 57 + 2 + 339 20 86, correo electrónico: dgomezp@univalle.edu.co (D. Gómez)
(Recibido el 1 de mayo de 2011. Aceptado el 10 de noviembre de 2011)
Resumen
La agrupación de personas en escenarios públicos puede producir vibraciones que generan incomodidad y, en algunas ocasiones, daños a la estructura. Entre las estructuras más vulnerables a esta excitación se encuentran las tribunas de los estadios de fútbol. Por este motivo se diseñó y construyó una tribuna con parámetros dinámicos similares a la tribuna sur del Estadio Olímpico Pascual Guerrero de Cali–Colombia, para representar a escala natural el efecto de las barras bravas al saltar coordinadamente sobre la gradería. En el trabajo descrito en este artículo se utilizó un actuador electromagnético con 13,2 kg de masa móvil y una estrategia de control activo para disminuir las vibraciones producidas por la interacción Humano/Estructura. La estructura junto con el controlador fueron modelados, identificados y validados experimentalmente. El desempeño del sistema de control se verificó en simulación y su estabilidad y robustez se comprobaron con ensayos experimentales con personas con una masa total hasta 232 kg. En los ensayos experimentales el sistema de control disminuyó la respuesta hasta en un 50% de los valores sin control.
Palabras clave: control estructural, control activo, identificación de sistemas, interacción dinámica humano/estructura, vibraciones
Abstract
The occupancy of structures by crowds often causes vibrations that in turn generate discomfort and, in some occasions, can cause damage to the structure. Football stadia are one type of structures that are especially vulnerable to such excitation and more so when they are used for other events such as concerts. As an experimental platform for investigating human–structure interaction, a grandstand was designed and built with dynamic parameters similar to the south grandstand of the Olympic Football Stadium in Cali Colombia. In the work described in this paper, an electro–magnetic actuator with a 13.2 kg active mass was used with an active control scheme to reduce human–induced vibrations in the grandstand. The structure and controller were modeled, identified and then validated experimentally. Performance of the control system was analyzed through simulations and then verified experimentally as a group of people, with a total mass of up to 232 kg, jumped on the grandstand. The control system reduced the structural response of the grandstand up to 50% of that without the control system.
Keywords:Structural control, active control, system identification, dynamic human/structure interaction, vibrations
Introducción
Actividades como saltar, bailar, caminar, correr y realizar ejercicios aeróbicos son actividades que comúnmente causan problemas de vibraciones en estructuras civiles. Este inconveniente se ha intensificado debido a la aparición de configuraciones estructurales más flexibles, con materiales más livianos y resistentes. Los análisis de vibraciones realizados para estos casos en [1, 2] coinciden en afirmar que los problemas son debidos a las bajas frecuencias naturales de la estructura, las cuales se encuentran en el rango de las frecuencias producidas por las personas en movimiento y representa un caso típico de resonancia. Este efecto se ha detectado en losas tipo steeldeck, en puentes peatonales, en graderías de estadios y plazas de toros [3].
La agrupación de grandes cantidades de personas en recintos cerrados o escenarios públicos se ha convertido en un tema de interés en la ingeniería estructural debido a que el movimiento de las personas produce vibraciones que pueden generar incomodidad y en algunas ocasiones pueden causar daños en la estructura [4]. Los problemas de vibraciones que ocurrieron en el año 2000 en la inauguración del puente Millenium en Londres representaron un punto de partida en el estudio del efecto que tienen las personas sobre la estructura. Estos estudios se basan en considerar a las personas no sólo como una fuerza externa sino como un sistema dinámico que altera las propiedades de la estructura. Los efectos producidos por esta interacción son conocidos en la literatura como efectos de Interacción Humano–Estructura y están relacionados con el tipo de estructura, el accionar de las personas ante diferentes tipos de excitaciones y condiciones ambientales y emocionales [3]. Un ejemplo de esto sucedió el 25 de abril de 2008 en el estadio Guillermo Plazas Alcid de Neiva, donde una parte de la tribuna occidental colapsó durante un concierto musical, causando la muerte de una persona y dejando a tres personas heridas [5] (ver figura 1).
Para disminuir las vibraciones en estructuras se puede modificar la respuesta al reforzar los elementos estructurales o al implementar un sistema de control [6]. Infortunadamente, reforzar la estructura aumentando las secciones de los elementos en pórticos de estadios y plazas de toros no es el método más adecuado debido al escaso espacio libre para recrecer los elementos estructurales, aun más cuando el problema no está en los pórticos sino en las losas que hacen las veces de tribunas. Por el contrario, la implementación de sistemas de control puede ser menos invasiva y más económica mediante la adecuación de dispositivos específicamente diseñados para disminuir las vibraciones [7], ya sea por el aumento del amortiguamiento del sistema o por el cambio en la frecuencia natural alejando la posibilidad de resonancia. Sin embargo, el uso e implementación de estos dispositivos mecánicos para controlen estructuras reales todavía es limitado. Según una encuesta sobre métodos de control de vibraciones realizada por Murray [8], los sistemas de control a menudo no han sido probados fuera de laboratorios o han tenido un impacto secundario en estructuras. Actualmente el uso de sistemas de control activo para reducir vibraciones en losas producidas por personas se ha implementado satisfactoriamente en laboratorio [9], demostrando que los sistemas de control pueden ser utilizados de manera eficaz para reducir vibraciones manteniéndolas en niveles confortables. En este artículo se describe el diseño, simulación e implementación de un sistema de control activo para disminuir las vibraciones producidas por personas al saltar de manera coordinada sobre una tribuna.
Descripción del sistema dinámico
Una tribuna con propiedades dinámicas similares a la tribuna sur del Estadio Olímpico Pascual Guerrero de Cali fue construida como plataforma experimental para este trabajo [10]. La tribuna tiene una masa muerta de 1082 kg y posee un sistema estructural formado por dos pórticos metálicos separados a dos metros. Cada pórtico está formado por dos columnas que forman una V asemejando la geometría del estadio Olímpico Pascual Guerrero, las cuales están conectadas por una viga cajón de 3,6 metros de longitud. Los pórticos se conectan mediante cinco viguetas con una lámina de alfajor en la parte superior para conformar el peldaño. A lado y lado de los pórticos existen voladizos de un metro de longitud en los que se ubicaron barandas puestas de manera independiente en cada peldaño (ver figura 2).
Las propiedades dinámicas de la tribuna fueron determinadas experimentalmente por Hernández en [10] mediante ensayos de vibración forzada para determinar cada una de las funciones de respuesta en el dominio de frecuencia. De esta manera se determinaron las variaciones en la respuesta de la tribuna ante las diferentes configuraciones del actuador electromagnético con masa activa de 13,4 kg (ver figura 3) que fue utilizado para producir las fuerzas de control sobre la estructura. La interacción dinámica entre el actuador y la estructura generalmente no es tenida en cuenta durante el diseño del controlador pero tiene una importante implicación en el rendimiento y estabilidad del mismo [11–13].
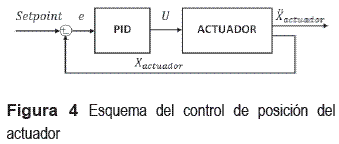
Debido a lo anterior, fue necesario diseñar un controlador de posición para mantener la masa activa en su setpoint o señal de referencia. Este controlador es necesario para evitar la saturación del actuador debido a la fuerza inercial que presenta su masa móvil cuando interactúa con la estructura. El algoritmo para controlar la masa móvil del actuador requiere una acción correctora que reduzca el error entre la señal enviada al actuador y la realizada por el mismo para lo cual se diseñó un controlador Proporcional–Integral– Derivativo (PID) usando retroalimentación de un LVDT que mide los desplazamientos de la masa activa. Los valores de las constantes del controlador son Kp=0,1, Ki=0,002 y Kd=0,08 y fueron seleccionados para cumplir dos criterios de diseño: el tiempo de subida tr ≤ 0,12s y un sobrepaso Mp ≤ 60%. En la figura 4 se muestra el diagrama de bloques del lazo de control de la posición de la masa móvil donde ![]() es la aceleración vertical en la mitad del peldaño bajo de la estructura, y
es la aceleración vertical en la mitad del peldaño bajo de la estructura, y 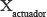 es el desplazamiento de la masa activa.
es el desplazamiento de la masa activa.
Las propiedades de la estructura con y sin actuador son resumidas en la tabla 1, donde se puede observar una disminución en la frecuencia natural de la estructura por la adición del peso del actuador y un cambio en el amortiguamiento cuando éste se encuentra encendido. El movimiento de la masa móvil del actuador apagado produce un incremento en el amortiguamiento. También se observa que cuando las masas del actuador son fijadas mecánicamente, los cambios en las propiedades dinámicas de la tribuna se ven reflejados sólo en la frecuencia natural por la adición de los 36 kg del actuador. Los cambios significativos en las propiedades dinámicas, particularmente en el amortiguamiento, se deben a la incorporación del controlador PID con referencia cero. La adición de este sistema dinámico (actuador y PID) aumenta la razón de amortiguamiento a 0,96% debido a la interacción control–estructura [12].
El modelo analítico de la estructura fue obtenido aplicando el método de identificación de sistemas descrito en [11] al ajustar funciones de transferencia a las funciones de respuesta de frecuencia mencionadas anteriormente. De esta manera la función de transferencia G(s) (ecuación 1) relaciona la perturbación producida por las personas saltando con la respuesta en aceleración de la tribuna y H(s) (ecuación 2) representa la función de transferencia entre la señal de control del actuador y la respuesta en aceleración de la tribuna. El modelo analítico de la estructura corresponde al sistema MISO de dos entradas–una salida conformado por G(s) y H(s) en la matriz de transferencia M(s) (ecuación 3). Mayor información del proceso de identificación del sistema se encuentra en [10].
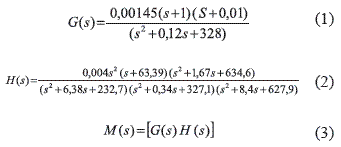
Diseño del controlador activo
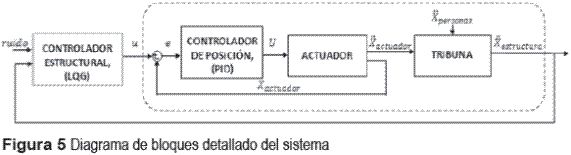
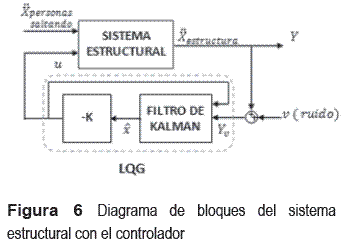
Posterior a la identificación y validación del modelo que describe el comportamiento dinámico del sistema estructural, se diseñó un controlador para reducir las aceleraciones verticales en la tribuna por medio de fuerzas generadas por el actuador. El diagrama de bloques del sistema con cada uno de los componentes se muestra en la figura 5, donde la línea punteada indica el sistema en lazo abierto (sin sistema de control estructural). El controlador es un Linear–Quadratic–Gaussian (LQG) para rechazo de disturbios. Un diagrama del sistema estructural, junto con el detalle de los componentes del controlador LQG encerrados por la línea punteada, se muestra en la figura 6, donde ![]() es la aceleración vertical en la mitad del peldaño bajo de la estructura,
es la aceleración vertical en la mitad del peldaño bajo de la estructura,  es la aceleración producidas por las personas al saltar, el Filtro de Kalman es el estimador de los estados del sistema y K es la ganancia óptima de realimentación de estados estimados utilizada para calcular la acción de control U [10].
es la aceleración producidas por las personas al saltar, el Filtro de Kalman es el estimador de los estados del sistema y K es la ganancia óptima de realimentación de estados estimados utilizada para calcular la acción de control U [10].
Para el diseño de controladores LQG sea plica el principio de separación que permite calcular por separado la ganancia K y el estimador de estados que posteriormente se combinan para formar el controlador. Para calcular K se utiliza una función de costo cuadrática que minimiza el siguiente índice de desempeño (ecuación 4).
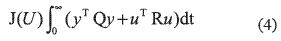
En esta ecuación Q y R son constantes que le dan peso a la minimización de la aceleración de la estructura (y) y la señal de control (u), respectivamente. Por otro lado se diseña el Filtro de Kalman definido en la ecuación 5.
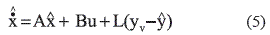
A y B son las matrices de estados del sistema estructural en el espacio de estados, es el vector de estados estimados, es la aceleración estimada de la estructura, es la aceleración medida y L es la ganancia del observador. Esta ganancia se calcula medianteuníndice de desempeño que minimiza la covarianza del error de estimación [10]. Finalmente, el controlador LQG queda definido por las ecuaciones 6 y 7.
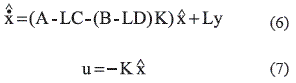
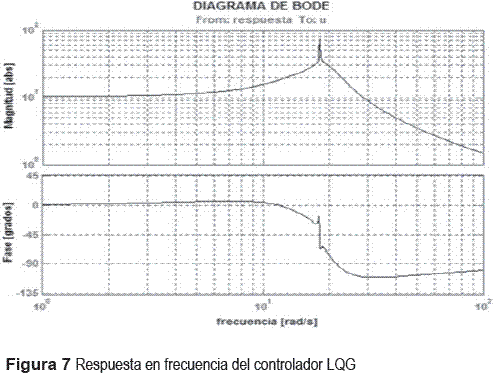
Aplicando las ecuaciones 4, 5, 6 y 7, se ajustó y validó el controlador LQG para el sistema MISO con los valores de Q=3000 y R=1. En la figura 7
Simulación del sistema de control activo
Anterior a la implementación del sistema de control, se hizo una verificación del diseño y desempeño del controlador mediante simulaciones, para realizar su validación experimental posteriormente. Para la simulación se utilizó el entorno de programación visual SIMULINK de MATLAB [14]. Se convirtió el controlador a un modelo en espacio de estados en tiempo discreto mediante la transformación bilineal usando un tiempo de muestreo de 2000 Hz. La valoración del controlador diseñado se basó en el índice de desempeño en términos de la media cuadrática de la respuesta (RMS). Con este índice se evaluó el porcentaje de reducción de la respuesta RMS de la estructura con control respecto a la misma sin control. Por lo tanto la cuantificación del índice de desempeño del controlador I está dada por la ecuación 8:
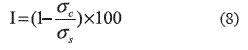
donde es la respuesta RMS de la estructura con control y es la respuesta RMS de la estructura sin control. Las simulaciones del sistema de control se realizaron para tres tipos de excitación:
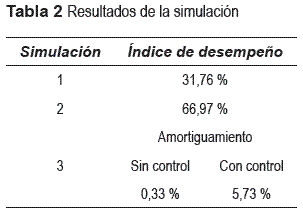
Los resultados para los tres tipos de simulaciones se presentan en la tabla 2 observándose la efectividad del sistema de control.
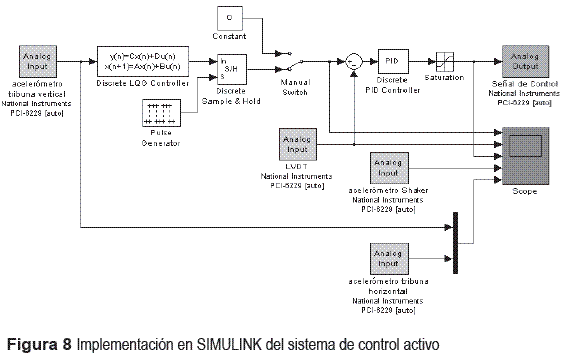
Implementación del sistema de control activo
Posterior a la verificación del desempeño del controlador para disminuir las vibraciones producidas por las personas en simulación, se realizó la implementación en la tribuna a escala real. Durante la implementación se utilizó el entorno SIMULINK y se compiló en una tarjeta Real–Time de alto desempeño de National Instruments (Ver figura 8). La tribuna fue excitada por los saltos producidos por una y tres personas. Se realizaron pruebas con el sistema de control apagado y encendido con el fin de valorar la respuesta de la estructura sin y con control. Teniendo ambas respuestas se evaluó el desempeño del sistema de control de acuerdo al porcentaje de reducción de la respuesta RMS expresado en la ecuación 8. En esta fase se realizaron las siguientes pruebas:
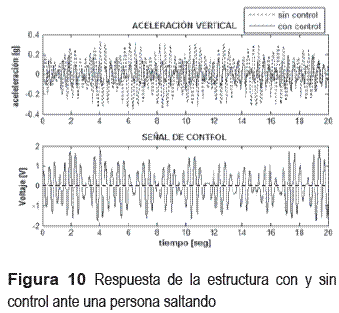
1. Una persona de 72 kg saltando en el segundo peldaño (ver figura 9). Los registros adquiridos durante este ensayo se muestran en la figura 10.
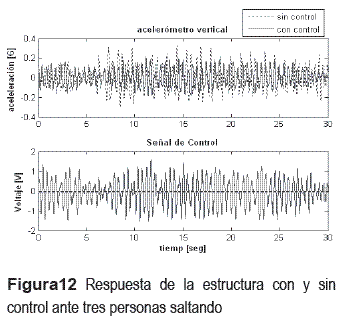
2. Tres personas con una masa total de 232 kg (ver figura 11) saltando coordinadamente sobre la tribuna (ver figura 12).
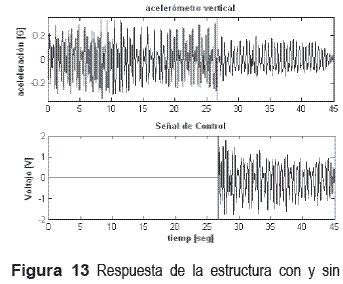
3. Tres personas saltando coordinadamente. El controlador inicialmente estaba apagado y luego se encendió, aproximadamente a los 27 segundos. La línea vertical en la figura 13 muestra el instante en el que es activado el controlador.
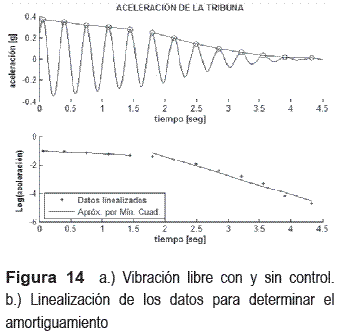
4. Un ensayo de vibración libre en el que el controlador se enciende segundos después de empezar las oscilaciones. En la linealización de los datos máximos mostrados en la figura 14.a, el cambio de amortiguamiento se ve reflejado en el aumento de la pendiente, pasando de un amortiguamiento sin control de 0,96% a uno de 7,56% con control (ver figura 14.b). El amortiguamiento de la estructura sin control corresponde al sistema en lazo abierto con referencia 0 enviada al actuador.
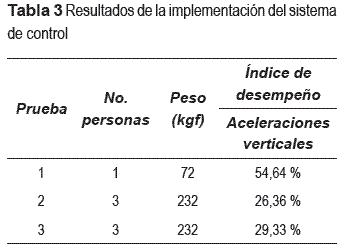
En resumen, los resultados de la implementación se muestran en la tabla 3.
Conclusiones
El sistema de control activo implementado en la tribuna demostró ser efectivo en reducir significativamente las vibraciones producidas por personas. Al utilizar una estrategia en cascada empleando un PID como lazo interno de control de posición del actuador y un controlador óptimo LQG como lazo externo de control estructural, se garantizó la estabilidad y robustez al presentarse cambios en la masa aportada por las personas. La estrategia de control para rechazo al disturbio se fundamentó en el controlador LQG que fue diseñado para disminuir las vibraciones verticales de la tribuna, logrando una reducción en la respuesta en RMS hasta en un 50% y un aumento de hasta 20 veces en la razón de amortiguamiento efectivo del sistema empleando un actuador electromecánico con una masa móvil de sólo el 1% de la masa total de la estructura. Para el salto coordinado de tres personas el índice de desempeño disminuye debido al aumento de la masa que está impactando a la estructura en cada salto, sin embargo el sistema de control respondió adecuadamente disminuyendo las aceleraciones verticales aun para este caso crítico.
Se enfatiza que esta tecnología aún está evolucionando y se esperan mejoras significativas tanto en los dispositivos como en los procedimientos correspondientes de diseño en los próximos años. En particular, la incorporación de requisitos en los códigos de construcción para la implementación de estos sistemas de control estructural es un paso que ya se está dando en países como Estados Unidos y Japón.
Agradecimientos
Los autores agradecen la financiación de la Universidad del Valle y COLCIENCIAS mediante el proyecto: ''Investigación y desarrollo tecnológico de sistemas de monitoreo y control estructural para reducir las vibraciones producidas por la interacción humano/ estructura''. (Contrato No. 003–2007).
Referencias
1. S. Ibrahimi, N. Haritos, E. F. Gad, J. L. Wilson. Floor Vibrations due to Human Excitation–Damping Perspective. Earthquake Engineering in Australia. Canberra 24–26. November. 2006. pp. 257–264. [ Links ]
2. P. Reynolds, P. A. Pavic, Z. Ibrahim. Changes of Modal Properties of a Stadium Structure Occupied by a Crowd. 22nd International Modal Analysis Conference (IMAC XXII). Dearborn. Detroit. USA. January, 2004. pp. 1–10. [ Links ]
3. A. Ortiz. Caracterización de Efectos de Interacción Humano/Estructura. Tesis de Maestría en Ingeniería Civil, Facultad de Ingeniería. Universidad del Valle. Santiago de Cali. 2011. pp. 93. [ Links ]
4. T. Ji. On the Combination of Structural Dynamics and Biodynamics Methods in the Study of Human–Structure Interaction. The 35th United Kingdom Group Meeting on Human Response to Vibration. Southampton, England. 2000. pp. 1–4 [ Links ]
5. A. Ortiz, D. Gómez, P. Thomson. ''Caracterización del Efecto de la Interacción Humano–Estructura en el Estadio Olímpico en Cali, Colombia''. Revista Ingeniería e Investigación. Vol. 29. 2009. pp. 13–23. [ Links ]
6. D. Gomez, J. Marulanda, P. Thomson. ''Sistemas de Control para la Protección de Estructuras Civiles Sometidas a Cargas Dinámicas''. Revista Dyna. No. 155. 2008. pp. 77–89. [ Links ]
7. A. Webster, R. Vaicajtis. ''Application of Tuned Mass Dampers to Control Vibrations of Composite–floor Systems''. Engineering Journal of the American Institute of Steel Construction. Vol. 29. 1992. pp. 116–124. [ Links ]
8. T. M. Murray. ''Building Floor Vibrations''. Engineering Journal. Vol. 28 (3). 1991. pp. 102–109. [ Links ]
9. L. M. Hanagan, T. M. Murray. Floor Vibration: A New Application for Active Control. Fourth Pan American Congress of Applied Mechanics. Buenos Aires. Argentina. Universidad del Salvador. 1995. pp. 7–12. [ Links ]
10. D. Hernández. Implementación de un Sistema de Control Activo para Reducir las Vibraciones Producidas por la Interacción Humano/Estructura en una Tribuna. Trabajo de grado (Ingeniero Civil), Facultad de Ingeniería. Universidad del Valle. Santiago de Cali. 2010. pp. 87. [ Links ]
11. D. Gómez. ''Comparison of Frequency Response and Neural Network Techniques for System Identification of an Actively Controlled Structure''. Revista Dyna. No. 170. 2011. [ Links ]
12. S. J. Dyke, L. M. Spencer. Implications of Control– Structure Interaction in Scaled Structural Control System Testing. International Conference on Control Applications. Kohala Coast–lsland of Hawai'i. Hawai'i. (USA). 1999. pp. 1–6. [ Links ]
13. D. Gómez, H. Moncayo, P. Thomson. Aspectos del Modelamiento de Estructuras para la Implementación de Sistemas de Control Activo. III Congreso Colombiano de Ingeniería Sísmica. Santiago de Cali. 2005. pp. 1–11. [ Links ]
14. MATLAB & SIMULINK version r2010a. The Math Works. Inc. Natick. MA. [ Links ]