Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.61 Medellín Dec. 2011
ARTÍCULO ORIGINAL
Active vibration control of vehicle suspension systems using sliding modes, differential flatness and generalized proportional–integral control
Control activo de vibraciones de sistemas de suspensión de vehículos usando modos deslizantes, planitud diferencial y control proporcional–integral generalizado
Esteban Chávez Conde1*, Francisco Beltrán Carbajal2, Antonio Valderrábano González3, Antonio Favela Contreras4
1Universidad del Papaloapan, Campus Loma Bonita. Av. Ferrocarril s/n, Ciudad Universitaria. C.P. 68400. Loma Bonita, Oaxaca, México.
2Universidad Autónoma Metropolitana. Unidad Azcapotzalco. Departamento de Energía. Av. San Pablo No. 180, Col. Reynosa Tamaulipas. C.P. 02200 México, D.F., México.
3Universidad Politécnica de la Zona Metropolitana de Guadalajara. C.P. 45640. Tlajomulco de Zúñiga, Jalisco, México.
4ITESM – Campus Monterrey. Departamento de Mecatrónica y Automatización Ave. Eugenio Garza Sada 2501 Sur, Col. Tecnológico. C.P. 64849. Monterrey, N.L., México.
*Autor de correspondencia: teléfono: 52 + 281 + 87 29 230 ext. 221, fax: 52 + 281 + 87 29 230 ext. 111, correo electrónico: echavez@unpa.edu.mx (E. Chávez)
(Recibido el 21 de Junio de 2011. Aceptado el 17 de noviembre de 2011)
Abstract
This paper presents a design approach of robust active vibration control schemes for vehicle suspension systems using differential flatness, sliding modes and Generalized Proportional–Integral control techniques to attenuate undesirable vibrations induced by irregular road disturbances. Two control schemes are proposed: one employing position and velocity measurements and other requiring only position measurements. Integral reconstruction of the time derivatives of the flat output up to third order is proposed to avoid the use of velocity and acceleration sensors, as well as information of unknown road disturbances.
Keywords:Active vehicle suspension system, sliding modes, differential flatness, generalized proportional–integral control
Resumen
En este artículo se presenta un enfoque de diseño de esquemas de control activo robusto para sistemas de suspensión de vehículos, usando técnicas de control Proporcional–Integral Generalizado, modos deslizantes y planitud diferencial, para atenuar vibraciones indeseables inducidas por perturbaciones de terreno irregular. Se proponen dos esquemas de control: uno de ellos emplea mediciones de posición y de velocidad y el otro requiere únicamente mediciones de posición. Se propone la reconstrucción integral de las derivadas de la salida plana para evitar el uso de sensores de velocidad y de aceleración, así como la información de perturbaciones de terreno desconocidas.
Palabras clave: sistema de suspensión activa de vehículo, modos deslizantes, planitud diferencial, control proporcional–integral generalizado
Introduction
The main objective on the active vibration control problem of vehicle suspension systems is to get security and comfort for the passengers by reducing to zero the vertical acceleration of the body of the vehicle. An actuator incorporated to the suspension system applies control forces to the vehicle body for reducing its vertical acceleration in active or semi–active way. The topic of active vehicle suspension control system has been quite challenging over the years and we refer the reader to some of the fundamental works in the vibration control areaand the references therein [1]. Some research works in this field propose control strategies like LQR in combination with nonlinear backstepping control techniques [2], which require information of the state vector (vertical positions and speeds of the tire and car body). A reduced order controller is proposed in [3] to decrease the implementation costs without sacrificing the security and the comfort by using accelerometers for measurements of the vertical movement of the tire and car body. In [4], a controller of variable gain that considers the nonlinear dynamics of the suspension system is proposed. It requires measurements of the vertical position of the car body and the tire, and the estimation of other states and the profile of the road. In addition, some interesting semiactive vibration control schemes, based on Electro– Rheological (ER) and Magneto Rheological (MR) dampers, have been proposed and implemented on commercial vehicles in [5, 6].
On the other hand, many dynamical systems exhibit a structural property called differential flatness. This property is equivalent to the existence of a set of independent outputs, called flat outputs and equal in number to the control inputs, which completely parameterizes every state variable and control input [7]. By means of differential flatness the analysis and design of controller is greatly simplified. In particular, the combination of differential flatness with sliding modes, which is extensively used when a robust control scheme is required, e.g., parameter uncertainty, exogenous disturbances and un–modeled dynamics [8], qualifies as an adequate robust control design approach to get high vibration attenuation level in active vehicle suspension systems. In this paper is proposed asuitable combination of differential flatness and sliding modes with the Generalized ProportionalIntegral (GPI) Control approach to design efficient and robust active vibration control schemes for vehicle suspension systems that only require information of the flat output.
GPI control, or control based on integral reconstructors of the unmeasured observable state variables, for the regulation and trajectory tracking tasks on time invariant linear systems was introduced by Fliess and co–workers in [9] as a generalization of classical PID control. This control design methodology has been extended to time–varying linear systems in [10] and, also, to a certain class of nonlinear systems [11]. The main objective is to avoid the use of traditional asymptotic state observers, or digital computations based on output samplings, therefore, the integral reconstructor–based feedback control laws are purely analog, requiring only measurements of the system output. The integral reconstruction of the state variables is carried out by means of elementary algebraic manipulations of the system model along with suitable invocation of the observability property. The purpose of the integral reconstructors is to get expressions for the unmeasured states in terms of inputs, outputs, and sums of a finite number of iterated integrals of the measured variables. In essence, constant errors and iterated integrals of such constant errors are allowed on these reconstructors. The current states thus differ from the integrally reconstructed states in time polynomial functions of finite order, with unknown coefficients related to the neglected and unknown, initial conditions. The use of these integral reconstructors in the synthesis of a state feedback controller needs suitable counteracting the effects of the implicit time polynomial errors. The destabilizing effects of the state estimation errors can be compensated by additively complementing a purely state feedback controller with a linear combination of a sufficient number of iterated integrals of the output tracking error, or output stabilization error. The closed loop stability is guaranteed by a simple characteristic polynomial assignment to the higher order compensated controllable and observable input–output dynamics.
In this paper is presented a design approach of robust active vibration control schemes for vehicle suspension systems using differential flatness, sliding modes and Generalized ProportionalIntegral control techniques to attenuate undesirable vibrations induced by unknown irregular road disturbances. In the control problem formulation is assumed that these perturbations are not available to implement a control scheme. Two control schemes are proposed. The first one requires information of the time derivatives of the flat output up to third order or measurements of all the state variables (displacements and velocities). The second controller only requires information of the flat output; the main idea is the use of integral reconstruction of the non– measurable state variables or the time derivatives of the flat output instead of state observers. This design approach results in robust active vibration control schemes against parameter uncertainties and exogenous disturbances. Simulation results are included to show the dynamic performance and robustness of the active control schemes proposed for a quarter–vehicle active suspension system.
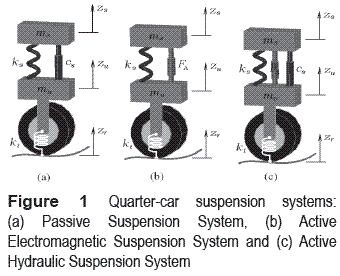
Quarter–Car suspension systems
Mathematical model of passive suspension system
A schematic diagram of a two degrees–of– freedomquarter–vehicle suspension system is shown in figure 1(a). The mathematical model of the passive suspension system is described by
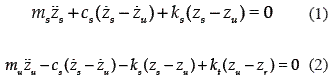
where the sprung mass ms represents the mass of the car–body part, the unsprung mass mu denotes the mass of the assembly of the axle and wheel, cs is the damper coefficient of suspension, ks and Kt are the spring coefficients of suspension and the tire, respectively, zs is the displacement of the sprung mass, zu is the displacement of the unsprung mass and zr is the terrain input disturbance.
Mathematical model of active electromagnetic suspension system
A schematic diagram of a quarter–car active electromagnetic suspension system is illustrated in figure 1(b). The electromagnetic actuator replaces the damper, forming a suspension with the spring [12]. The friction force of an electromagnetic actuator is neglected. The mathematical model of an electromagnetic active suspension system is given by
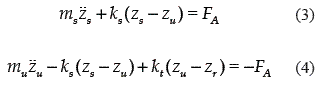
where FA is the electromagnetic actuator force, which is considered as the control input.
Mathematical model of hydraulic active suspension system
Figure 1(c) shows a schematic diagram of a quarter–car active hydraulic suspension system. The mathematical model of this active suspension system is given by
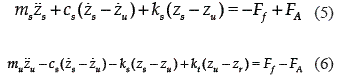
where FA is the hydraulic actuator force and Ff is the friction force generated by the seals of the piston with the cylinder wall inside the actuator. This friction force has a significant magnitude (> 200N) and cannot be ignored [5, 12].
Defining the state variables x1= zs, x2 = zs, x3 = zuand x4 = zu, one obtains the following state–space description:
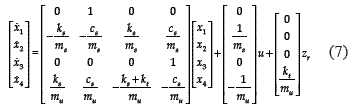
The net force provided by the hydraulic actuator as control input u = FA – Ff is the difference between the hydraulic force FA and the friction force Ff.
Sliding mode–differential flatness control of hydraulic suspension system
The hydraulic suspension system is controllable and, therefore, differentially flat [13] with a flat output constructed as a linear combination of the displacements of the body of the car and wheel [14, 15]:
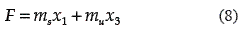
In our analysis zr is considered as an unknown exogenous perturbation signal due to irregular road surfaces with uniformly bounded magnitude for all t » 0, i.e., 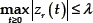 , which could be suppressed or at least attenuated by the sliding mode–based GPI control action. In fact, our design approach pursues to exploit the sliding mode control methodology for design of robust suspension system controllers with respect to unmodeled additive bounded perturbation input signals and parametric uncertainties.
, which could be suppressed or at least attenuated by the sliding mode–based GPI control action. In fact, our design approach pursues to exploit the sliding mode control methodology for design of robust suspension system controllers with respect to unmodeled additive bounded perturbation input signals and parametric uncertainties.
Then, all the unperturbed system variables can be parameterized in terms of the flat output and a finite number of its time derivatives as follow,
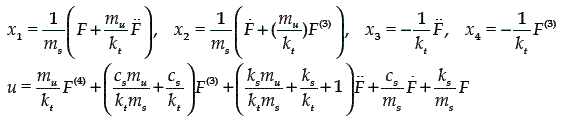
From this differential parameterization, we get the following input–output differential equation:
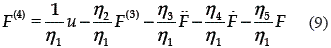
where
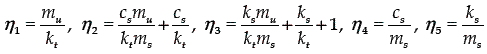
Now, consider the traditional sliding surface,
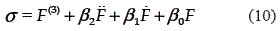
which is chosen so that the error dynamics restricted to σ = 0 is governed by the desired linear differential equation,
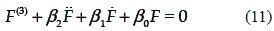
The design gains β2,..., β0 are selected to verify that the associated characteristic polynomial s3 + β2s2 + β1s + β0 be Hurwitz. As a consequence, the error dynamics on the switching surface σ = 0 is globally asymptotically stable. The sliding surface σ = 0 is made globally attractive with the continuous approximation to the discontinuous sliding mode controller as given in [16], i.e., by forcing the system to satisfy the dynamics,
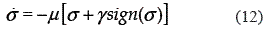
where µ, γ denote positive real constants and "sign" is the standard signum function. Indeed, for σ ≠ 0, and using the Lyapunov function V = (1/2)σ2, we have that 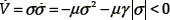
Therefore a sliding regime is guaranteed to exist on σ = 0 for all time t after the finite hitting time th [8]. Moreover, if the differentially flat linear vehicle suspension system dynamics is subjected to the bounded unknown perturbation input signal ξ (t), it easy to prove, using the Lyapunov function V = (1/2)σ2 and choosing W = µγ>supt |ξ(t)|, the asymptotic convergence of σ to the sliding surface σ = 0. Indeed, 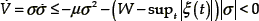 .
.
One then obtains from (9) the following sliding– mode controller:
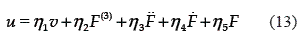
with 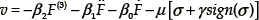 .
.
This controller requires measurements of all the state variables of the suspension system, zs, żs, zu and żu corresponding to the vertical positions and velocities of the body of the car and the tire, respectively.
In addition, the controller (13) can also be implemented for the active electromagnetic suspension system given by the equations (3) and (4), where the damper and the hydraulic actuator are replaced by an electromagnetic actuator, forming with the spring an oil–free suspension [12]. In this case, the control input u is the force FA supplied by the electromagnetic actuator, i.e., u = FA.
Sliding mode–GPI control of hydraulic suspension system
An integral input–output parameterization of the time derivatives of the flat output, is given, modulo initial conditions, by
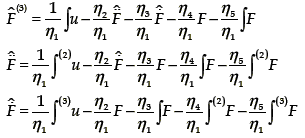
These expressions are obtained by successive integrations of the equation (9). For simplicity, we
have denoted the integral ∫0t Ø(τ)dτ by ∫Ø and ∫0t∫0σ1…∫0σn–1Ø(σn)dσn … dσ1 by ∫(n)Ø with n a positive integer.
The relationships between the state variables and the integrally reconstructed state variables are given by
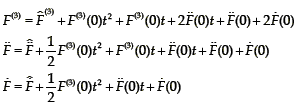
where F(3) (0), 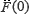 and
and 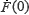 are all real constants depending on the unknown initial conditions.
are all real constants depending on the unknown initial conditions.
The sliding surface inspired on the GPI control can be proposed as,
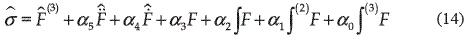
The last integral term yields error compensation, structural estimation errors. The ideal sliding eliminating destabilizing effects, those of the condition 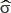 = 0 results in a sixth order dynamics,
= 0 results in a sixth order dynamics,
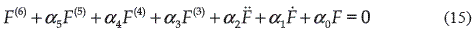
The gains of the controller α5,..., α0 are selected so that the associated characteristic polynomial s6 + α5s5 + α4s4 + α3s3 + α2s2 + α1s + α0 is Hurwitz. As a consequence, the error dynamics on the switching surface 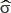 = 0 is globally asymptotically stable.
= 0 is globally asymptotically stable.
The sliding surface 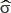 = 0 is made globally attractive with the continuous approximation to the discontinuous sliding mode controller as given in [16], i.e., by forcing to satisfy the dynamics,
= 0 is made globally attractive with the continuous approximation to the discontinuous sliding mode controller as given in [16], i.e., by forcing to satisfy the dynamics,
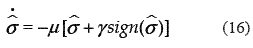
where μ and γ denote real positive constants. As before, the sliding surface is globally attractive, 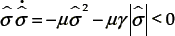 for
for 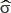 ≠ 0. Then the following sliding–mode controller is obtained:
≠ 0. Then the following sliding–mode controller is obtained:
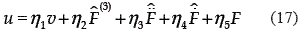
with
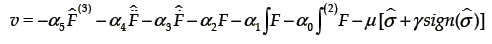
This controller requires only the measurement of the variables of the states zs and zu corresponding to the vertical displacements of the car body and the wheel, respectively.
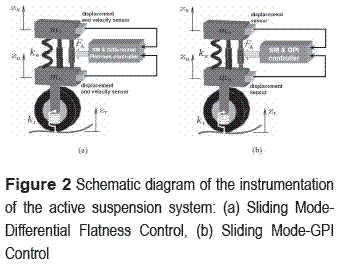
Instrumentation of active suspension system
Measurements Required
The variables only required for implementation of the proposed Sliding Mode–GPI controller are the vertical displacement of the body of the car zs, and the vertical displacement of the wheel zu. These variables are needed to be measured by sensors. On the other hand, for implementation of the proposed Sliding Mode–Differential Flatness controller, are needed to measure the vertical displacement of the body of the car and the wheels, as well as the velocities of the body of the car żs, and the wheel żu.
Using Sensors
In [17], the use of sensors in experimental vehicle platforms, as well as in commercial vehicles is presented. The most common sensors, used for measuring the vertical displacement of the body of the car and the wheels, are laser sensors. This type of sensor could be used to measure the variables zs and zu needed for implementation of the controllers. Accelerometers or other types of sensors are needed to get information of the velocity signals żs and żu. In the Sliding Mode–GPI Control scheme, the velocity variables are estimated with the use of integral reconstructors from the knowledge of the control input, the flat output and the differentially flat system model.
A schematic diagram of the instrumentation of the active suspension system is illustrated in figure 2.
Simulation results
The simulation results were obtained by means of MATLAB/Simulink®, with the Runge–Kutta numerical method and a fixed integration step of 1 ms.
Parameters and type of road disturbance
The numerical values of the quarter–car suspension model parameters [18] chosen for the simulations are shown in table 1.
The following trajectory was utilized to simulate the unknown exogenous disturbance excitations due to irregular road surfaces [18]
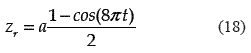
where a is the bump amplitude, which is set to be a = 0.11 [m] for 0.5 ≤ t ≤ 0.75, a = 0.55 [m] for 3.0 ≤ t ≤ 3.25 and 0 otherwise.
The desired robust performance of the closed– loop vehicle suspension system is to reduce as much as possible the car–body vibrations induced by the road surface perturbation.
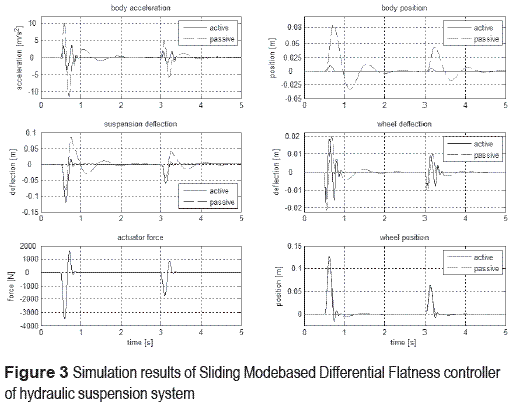
Sliding mode–differential flatness controller performance
It is desired to stabilize the system in the positions zs = 0 and zu = 0. The controller gains (13) were obtained by forcing the closed–loop characteristic polynomial to be given by the following Hurwitz polynomial:
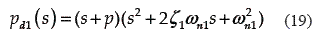
with p = 100, ζ1 = 0.5, ωn1 = 90, μ = 95 and γ = 95. The simulation results are illustrated in figure 3. It can be seen a high vibration attenuation level of the active vehicle suspension system (car–body acceleration and position) compared with the passive counterpart. Moreover, one can observe the active suspension deflection response to compensate the road surface perturbation force, and that supt |x1 – x3|< a, where a is the bump amplitude.
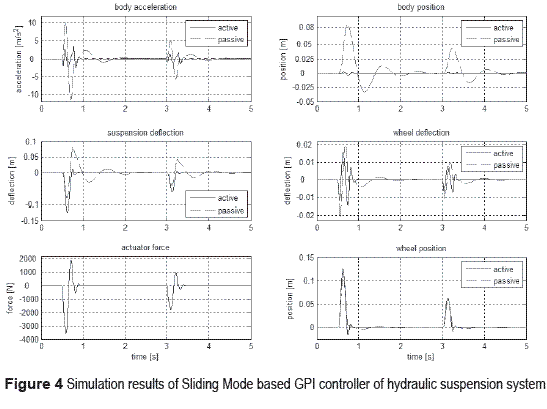
Sliding mode–GPI controller performance
It is desired to stabilize the system in the positions zs = 0 and zu = 0. The controller gains (17) were obtained by forcing the closed–loop characteristic polynomial to be given by the following Hurwitz polynomial:
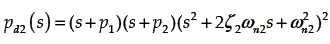
with p1 = 90, p2= 90, ζ2= 0.9, ωn2 = 70, μ = 95 and γ = 95. The performance of the sliding mode based GPI controller is depicted in figure 4. One can see the high attenuation level of road–induced vibrations with respect to passive suspension system.
Conclusiones
In this paper we have presented a design approach of robust active vibration control schemes for vehicle suspension systems based on Generalized Proportional–Integral control, differential flatness and sliding modes. Two control schemes have been proposed to attenuate the vibrations induced by unknown exogenous disturbance excitations due to irregular road surfaces. Integral reconstruction is employed to get structural estimates of the time derivatives of the flat output, needed for the implementation of the controllers proposed. The simulation results show that the stabilization of the vertical position of the quarter of car is obtained within a period of time much shorter than that of the passive suspension system. The fast stabilization with amplitude in acceleration and position of the body of the car is observed. Finally, the robustness of the controllers to stabilize to the system before the unknown disturbance is verified.
Referencias
1. M. Ahmadian. ''Active control of vehicle vibration''. Encyclopedia of Vibration. S. G. Braun, D. J. Ewins, S. S. Rao (editors) Vols. 1–3.Ed. Academic Press. San Diego, CA. 2001. pp. 37–45. [ Links ]
2. Z. Liu, C. Luo, D. Hu. Active Suspension Control Design Using a Combination of LQR and Backstepping. Proceedings of 25th IEEE Chinese Control Conference. Harbin, Heilongjiang. August 7–11. 2006. pp. 123–125. [ Links ]
3. A. Yousefi, A. Akbari, B. Lohmann. Low Order Robust Controllers for Active Vehicle Suspensions. Proceedings of IEEE International Conference on Control Applications. Munich, Germany. October 4–6, 2006. pp. 693–698. [ Links ]
4. Tahboub, A. Karim. Active Nonlinear Vehicle– Suspension Variable–Gain Control. Proceedings of 13th IEEE Mediterranean Conference on Control and Automation. Limassol. Cyprus. June 27–29, 2005. pp. 569–574. [ Links ]
5. S. Choi, H. Lee, E. Chang. ''Field test results of a semi–active ER suspension system associated with skyhook controller.'' Mechatronics. Vol. 11. 2003. pp. 345–353. [ Links ]
6. G. Yao, F. Yap, G. Chen, W. H Li, S. Yeo. ''MR damper and its application for semi–active control of vehicle suspension system.'' Mechatronics. Vol. 12. 2002. pp. 963–973. [ Links ]
7. M. Fliess, J. Lévine, Ph. Martin, P. Rouchon. ''Flatness and defect of nonlinear systems: introductory theory and examples.'' Int. Journal of Control. Vol. 61. 1993. pp. 1327–1361. [ Links ]
8. V. Utkin. Sliding Modes and Their Applications in Variable Structure Systems. Ed. MIR Publishers. Moscow (Russia). 1978. pp. 1–166. [ Links ]
9. M. Fliess, R. Márquez, E. Delaleau, H. Sira. ''Correcteurs Proportionnels–Integraux Généralisés.'' ESAIM Control, Optimisation and Calculus of Variations. Vol. 7. 2002. pp. 23–41. [ Links ]
10. H. Sira, G. Silva. ''Regulation and Tracking for the Average Boost Converter Circuit: A Generalized Proportional Integral Approach.'' International Journal of Control. Vol. 75. 2002. pp. 988–1001. [ Links ]
11. H. Sira. On the generalized PI control of some nonlinear mechanical systems. Proceedings of IEEE American Control Conference, Anchorage. Alaska. 2002. pp. 839–844. [ Links ]
12. I. Martins, J. Esteves, D. Marques, F. Da Silva. ''Permanent–Magnets Linear Actuators Applicability in Automobile Active Suspensions.'' IEEE Trans. on Vehicular Technology. Vol. 55. 2006. pp. 86–94. [ Links ]
13. H. Sira, K. Agrawal. Differentially Flat Systems. Ed. Marcel Dekker. N.Y. 2004. pp. 1–214. [ Links ]
14. E. Chávez, F. Beltrán, A. Blanco, H. Méndez. Sliding Mode and Generalized PI Control of Vehicle Active Suspensions. Proceedings of 18th IEEE International Conference on Control Applications. Saint Petersburg, Russia. 2009. pp. 1726–1731. [ Links ]
15. E. Chávez, F. Beltrán, C. García, A. Blanco. Sliding Mode based Differential Flatness and State Estimation of Vehicle Active Suspensions. Proceedings of 6th International Conference on Electrical Engineering, Computing Science and Automatic Control. Toluca, México. 2009. pp. 544–549. [ Links ]
16. H. Sira Ramirez. ''A dynamical variable structure control strategy in asymptotic output tracking problems.'' IEEE Trans. on Automatic Control. Vol. 38. 1993. pp. 615–620. [ Links ]
17. A. Chamseddine, H. Noura, T. Raharijaona. Control of Linear Full Vehicle Active Suspension System Using Sliding Mode Techniques. Proceedings of IEEE International Conference on Control Applications. Munich, Germany. October 4–6, 2006. pp. 1306–1311. [ Links ]
18. Y. Sam, K. Hudha. Modelling and Force Tracking Control of Hydraulic Actuator for an Active Suspension System. Proceedings of 1st IEEE Conference on Industrial Electronics and Applications (ICIEA’2006). Singapore. May 24–26, 2006. pp. 1–6.