Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230On-line version ISSN 2422-2844
Rev.fac.ing.univ. Antioquia no.61 Medellín Dec. 2011
ARTÍCULO ORIGINAL
Description of execution time dynamics for a set of concurrent real–time tasks
Descripción de la dinámica de los tiempos de ejecución de un conjunto de tareas en tiempo real concurrentes
Pedro Guevara López1, José de Jesús Medel Juárez2, Gustavo Delgado Reyes1
1ESIME–IPN. Av. Santa Ana No. 1000. San Francisco Culhuacán. C.P. 04430 México D.F.
2CIC, Col. Nueva Industrial Vallejo. C.P. 07738. México D. F.
*Autor de correspondencia: teléfono: + 52 + 55 +562 420 00 ext. 73250, fax: + 52 + 55 + 565 620 58, correo electrónico: pguevara@ipn.mx (P. Guevara)
(Recibido el 1 de mayo de 2011. Aceptado el 17 de noviembre de 2011)
Abstract
A Real–time System (RTS) implemented in a digital computer interacts with the physical world through knowledge variables (sensors, actuators, Analogical – Digital, and Digital–Analogical convertors) processing its requirements through real–time tasks (Ji: i Z+). Each Ji. is formed by a set of instances {ji,k: i,k
Z+). Each Ji. is formed by a set of instances {ji,k: i,k Z+, i is the task index, k is the instance index} with at least three time constraints: arrival, execution and, interval times (Li,k, Ci,k, Di,k). The execution time identification Ĉi,k, is based on Instrumental Variable parameter estimation and the recursive state space ARMA model. The execution times were measured experimentally using a Real–time Operative System QNX 6.5 Neutrino in an Intel Core i7 processor with a speed of 2.66 GHz. This paper presents a state of the art real–time task model, execution time measurements, an Instrumental Variable parameter estimator on recursive state space identification, experimentation and, results.
Z+, i is the task index, k is the instance index} with at least three time constraints: arrival, execution and, interval times (Li,k, Ci,k, Di,k). The execution time identification Ĉi,k, is based on Instrumental Variable parameter estimation and the recursive state space ARMA model. The execution times were measured experimentally using a Real–time Operative System QNX 6.5 Neutrino in an Intel Core i7 processor with a speed of 2.66 GHz. This paper presents a state of the art real–time task model, execution time measurements, an Instrumental Variable parameter estimator on recursive state space identification, experimentation and, results.
Keywords: Tasks, Real–time, estimation, identifier, computing time, instance, error
Resumen
Un Sistema en Tiempo Real (STR) implantado en una computadora digital, interactúa con el mundo físico a través del acondicionamiento de variables (sensores, actuadores convertidores Analógico/Digital A/D y Digital/Analógico D/A) y procesa sus peticiones mediante tareas en tiempo real (Ji: i Z+). Cada Ji, está formada por un conjunto de instancias { ji,k: i,k
Z+). Cada Ji, está formada por un conjunto de instancias { ji,k: i,k Z+, i es el índice de la tarea, k es el índice de la instancia} con al menos tres restricciones temporales: tiempo de arribo, tiempo de ejecución y plazo (Li,k, Ci,k, Di,k). En este sentido, es importante proponer un modelo para reconstruir el comportamiento de los tiempos de ejecución Ci,k. El modelo propuesto es un ARMA con un estimador de parámetros basado en la variable instrumental. Los tiempos de ejecución fueron medidos experimentalmente en QNX Neutrino 6.5 utilizando un procesador Intel Core i7 de 2.66 GHz. Se presentan los antecedentes teóricos del modelado de tareas en tiempo real, las mediciones de tiempo de ejecución, el modelo de tiempos de ejecución, el estimador de parámetros con variable instrumental, la experimentación y los resultados.
Z+, i es el índice de la tarea, k es el índice de la instancia} con al menos tres restricciones temporales: tiempo de arribo, tiempo de ejecución y plazo (Li,k, Ci,k, Di,k). En este sentido, es importante proponer un modelo para reconstruir el comportamiento de los tiempos de ejecución Ci,k. El modelo propuesto es un ARMA con un estimador de parámetros basado en la variable instrumental. Los tiempos de ejecución fueron medidos experimentalmente en QNX Neutrino 6.5 utilizando un procesador Intel Core i7 de 2.66 GHz. Se presentan los antecedentes teóricos del modelado de tareas en tiempo real, las mediciones de tiempo de ejecución, el modelo de tiempos de ejecución, el estimador de parámetros con variable instrumental, la experimentación y los resultados.
Palabras clave: Tarea, tiempo real, estimador, identificador, tiempo de ejecución, instancia, error
Introduction
Real–Time Systems (STR) are present in industrialized societies in all electronic devices: televisions, washing machines, microwave ovens, cell phones and digital telephone exchanges; airplanes, trains, automobiles, ensuring the processes considered safety in general operations. In [1], a Real Time System (RTS) actively interacts with the environment with time constraints. The RTS implanted in a Real Time Operating System (RTOS) such as QNX Neutrino is formed by a set of instances {ji,k} inside of a real time task Ji, where i is the index belonging to the task and, k is the instance index. Each instance is started by a service request.
The model considers the dynamic properties to describe execution times Ci,k determining the processor usage in each task.
Modeling execution time of real–time tasks
This work was developed in QNX Neutrino 6.5, modeling real–time tasks, considering time constraints. The STR implanted a QNX Neutrino operating system, composed of a set of concurrent tasks. The turnout has the potential parallelism in the execution tasks when their number exceeds the number of processors available by computer. The RTOS QNX Neutrino is complete and robust according to [2], and is adaptable to the resource constraints of embedded RTS.
The paper described in [3] summarizes what some authors consider the specific execution times for the worst case (WCET) and not as alternatives to probabilistic behavior, describing the execution times and duration periods of a real–time task. In [1], real–time tasks are classified according to time constraints, considering the arrival time, execution and deadline times. These are classified as periodic, sporadic and non periodic tasks according to time conditions. In [4], the models were limited considering fixed execution times, but the variations were different between the identified and the results of the computer system. In [5], an identification of the worst case execution time (WCET) considered the variations due to external factors, such as, pipeline, route search, loop number, and mutual exclusion. In [6], a WCET probability distribution function tool analyzed this in a real–time program, depending on factors such as, memory cache, forecasts, pipelines and other interactions. In [7], a stochastic ARMA model represented the behavior of arrival times, estimating the parameter using a digital filter.
Real–time tasks time constraints
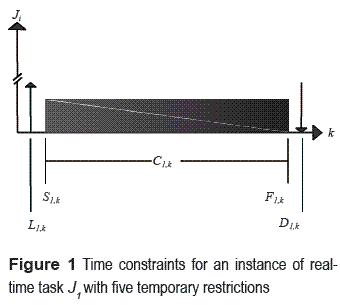
In [1], a real–time task Ji it is described as an executable job entity characterized by arrival times and restriction times associated with an instance. Where i is the task index, and k represents the instance index related to a time interval according to Nyquist [8]. The real–time task is defined by the following quintuple (Li,k, Si,k, Ci,k, Fi,k, Di,k), i,k  Z+ where the temporal conditions are arrival Li,k, start Sk and, execution time Ci,k in which the system finishes its operations in completion time Fi,k and bounded by maximum deadline Di,k. Figure 1 shows a block diagram with temporal elements that make up an instance of a real–time task.
Z+ where the temporal conditions are arrival Li,k, start Sk and, execution time Ci,k in which the system finishes its operations in completion time Fi,k and bounded by maximum deadline Di,k. Figure 1 shows a block diagram with temporal elements that make up an instance of a real–time task.
Execution time model for real–time task
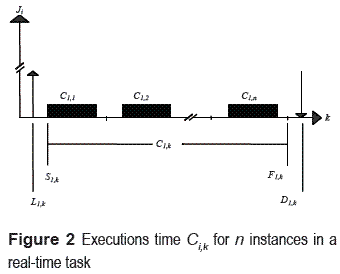
Execution time Ck is the time in which the instance with index k of a real–time task Ji computing its operations, disregarding the preemption task, this is shown in figure 2.
The execution time vector Ck of a set of concurrent real–time tasks J for an k interval is defined in (1).
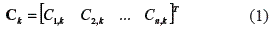
In [9], the states contain disturbance errors read by the receiver (oscilloscopes, data acquisition cards, etc.), influenced by the environment surrounding sender and receiver. In [5, 6] consider variations of the execution times due to the search for the best execution path and other internal interactions. In [10], the disturbances are due to events outside the digital system, and were medeled based on [1] with an ARMA described in (2) and (3).
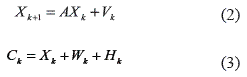
Where Ck is a execution time of set of concurrent real–time task in the k–th instance, Ak is the system parameter, Vk is a computer internal noise, Wk is a computer external noise, Hk is a execution time reference and Xk is an internal execution time model state. Recursive execution time from a concurrent real–time task is described in Theorem 1 and (4).
Theorem 1. The concurrent real–time task described by (2) and (3), has a recursive execution time form (4).
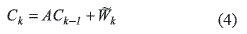
Where 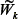 represent the generalized noises.
represent the generalized noises.
Proof. Assume that Xk+1 described in (2) is delayed in time and yields (5).
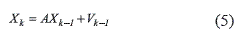
From (3), the internal state of the run–time function Ck is achieved with a delay (6).
Caracterización de los polvos cerámicos
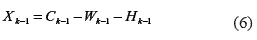
With (6) in (5), it is possible to obtain (7).
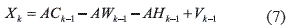
With (7) in (3), it is possible to obtain (8).
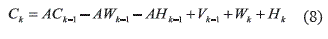
In (8), it is describe 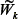 = AWk–1 – AHk–1 + Vk–1 + Wk + Hk, as generalized noises. ■
= AWk–1 – AHk–1 + Vk–1 + Wk + Hk, as generalized noises. ■
The recursive execution time form (4) has an explicit matrix parameter A with respect to concurrent real–time task response times. The generalized noises 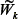 would only be described affecting the response, through internal gains excitation.
would only be described affecting the response, through internal gains excitation.
Instrumental variable execution times parameter estimation
In [9], the black box system has an estimation process, based on matrix digital filter description. In [11], three parameter estimator comparisons were presented: Recursive Least Squares (MSM), Recursive Gradient (MGR) and, Instrumental Variable Methods (MVI).
Theorem 2. A concurrent real–time task parameters execution time model according to (6) and using an instrumental variable is presented in (9).

Where the estimator (9) is represented considering the second probability stage ![]() and
and 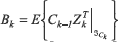 , respectively.
, respectively.
Proof. According to (4) using the second probability moment, (10) is obtained.
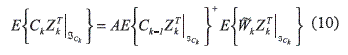
The properties described in (11) and (12) satisfy (10)
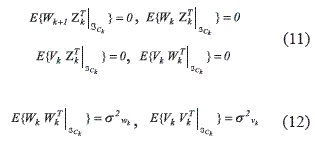
Where Zk is the instrumental variable according to [11], described in (13).
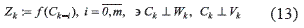
From expression (10), pseudo–inverse of Bk allows describing the internal gain (9). The recursive form of Pk and Bk is shown in (14) and (15), respectively.
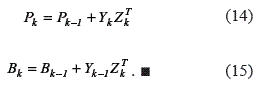
Theorem 3. The estimator described in (9) uses the instrumental variable and converges at almost all points, shown in (16).

Proof. According to the execution times of a concurrent real–time recursive form task described in (4), the identifier Ĉk is formed in (17)

This leads to the conclusion that the identification error is described in (18).
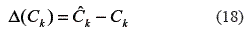
Considered (4) and (17) in (18), the difference resulted in (19).
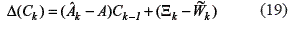
The stochastic gradient of (19) with respect to execution time, obtains (16). ■
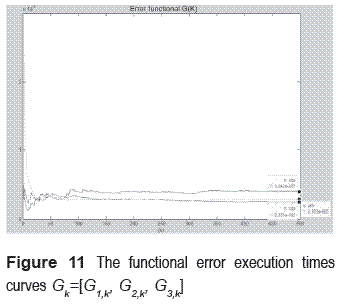
The functional error Gk described in (20) was obtained considering the second probability moment, in recursive form.
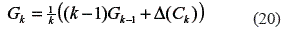
Resultados y discusión
In [12], different methods of measuring the performance of the instances execution times of a real–time task are presented. It used a clock () function in library time.h in the POSIX systems. This method has the advantage of more information details configured as a clock resolution in milli–seconds of the program code shown in figure 3. In this investigation, execution times were measured experimentally in the QNX® Neutrino RTOS 6.5 system, using an Intel® Core i7 2.66 GHz. The experiment under consideration is the simulation of a DC motor described in (21) and presented in more detail in [13].
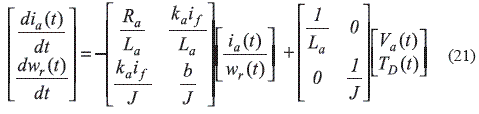
Where ia (A) is the armature current, wr (rad /sec) angular velocity, Ra (Ω) armature resistance, The La (H) armature inductance, J (kgm2) torque, ε the difference conditions, if (A) is the stator current, ka engine construction, b constant friction viscosity, Va (V) armature voltage, TD (Nm) motor load.
The state space (27) was discreetly computed considered finite differences, becoming in (22).
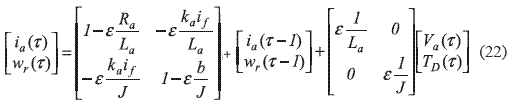
(22) is transformed symbolically in state space shown in (23).
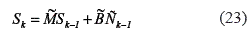
Where the matrix parameters 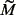 and
and 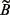 are shown in (24).
are shown in (24).
The simulation considered the variables involved in (4) and (5), which were programmed using a proportional controller, establishing a measurement governed by the International Units System shown in table 1.
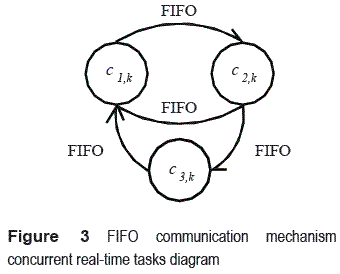
Three tasks were scheduled in a vector: Ck= [C1,k, C2,k, C3,k]T for DC motor dynamics simulation, according to equations (9), (14), (15) and, (22), where the matrix parameter was obtained in (25), and applied in (4) describing the identification k. The communications among tasks are performed by FIFO pipelines as shown in figure 3.
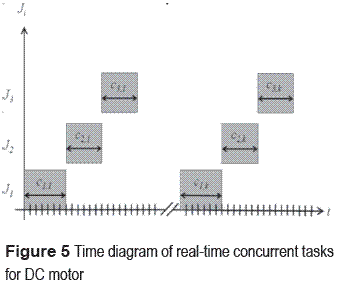
Each task is executed in a different QNX terminal, shown in figure 4. The simulation results considering the torque load due: TD = 0 Nm, a reference voltage = 110V and a gain in the feedback, k = 1.36, presenting the first 20 instances.
This work measures the execution time tasks C1,k, C2,k, C3,k, (see figure 5). A proposed of the dynamics through (4) and parameter estimation of execution times according to (9) obtained the results shown in figure 6.
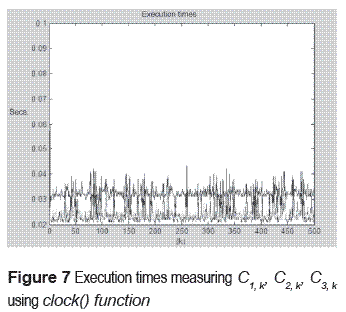
Figure 7 shows three execution times measured of the algorithm programmed into the real–time QNX operating system, using the code segment shown in figure 6, through 500 instances. The three execution time shown in this figure correspond to each processes that were implemented using the Real–time Operative System QNX 6.5 Neutrino.
The matrix filter estimation result (25) was based on an instrumental variable applied in (9).
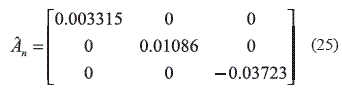
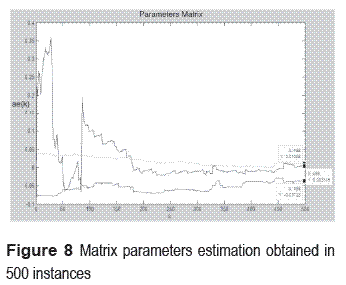
The matrix parameter evolution is shown in figure 8, in addition this matrix presents the three estimated parameters obtained thru instrumental variable technique.
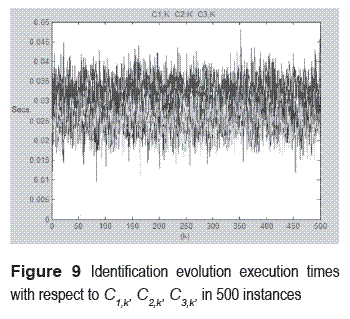
The matrix parameters (25) applying in (4) instead of A, transform to the recursive execution time model (4) in an identifier with non–correlated disturbances (26), and the resulting matrix can be seen in figure 9, in which it is propose the recursive way to model the execution times of the real time task presented in this paper.
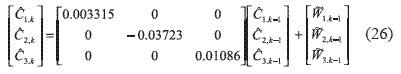
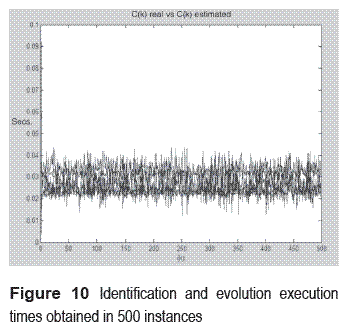
The execution times and its identifications results, in 500 instances are shown in figure 10. This figure in fact is a comparison between the execution times obtained using the code shown in figure 6, and the execution times obtained thru instrumental variable technique.
Conclusiones
Real–time tasks are made up of instances. They have the problem of how to describe their dynamic execution times considering a clock () function. An illustrative simulation model of a DC motor using finite difference described in (22) was proposed, and demonstrated that the system had three concurrent tasks as shown in figure 4. The reconstruction of the execution times was very successful, based on the functional error convergence levels. Execution time of a real–time task in which the internal parameter A with respect to (2) is reflected in (3) and explicitly seen in (4) allows considering the estimation process, based on the reconstruction ARMA model achieved good execution times. Additionally this included the functional error concept described by (20). This concept is a comparison between the execution times shown in figure 9 and measured execution times shown in figure 7, this determines that the smaller the functional error, the greater the accuracy of the reconstruction achieved through a proper process of matrix system estimation. Therefore one of the important contributions of this paper is the successful reconstruction of the three scheduled execution time tasks, and the functional error vector obtained is very small so conclusively the smaller is the functional error vector, the better reconstruction it is obtained, as it is demonstrated in figure 11.
Referencias
1. J. Medel, P. Guevara, D. Cruz. Temas Selectos de Sistemas en Tiempo Real. Ed. Politécnico. México. 2007. pp. 59–70. [ Links ]
2. R. Krten. QNX Neutrino RTOS Getting Started with QNX Neutrino: A Guide for Realtime Programmers. QNX Software Systems International Corporation. Ontario. 2008. pp. 23–24. [ Links ]
3. C. Liu, J. Layland. ''Scheduling algorithms for multiprogramming in a Hard Real Time System Environment.'' Journal of the ACM. Vol. 20. 1973. pp. 46–61. [ Links ]
4. S. Manolache, P. Eles, Z. Peng. ''Schedulability Analysis of Applications with Stochastic Task Execution Times.'' ACM Transactions on Embedded Computing Systems. Vol. 3. 2004. pp. 706–735. [ Links ]
5. F. Stappert, P. Altenbernd. ''Complete Worst–Case Execution Time Analysis of Straight–line Hard RealTime Programs.'' Journal of Systems Architecture. Vol. 46. 2000. pp. 339–355. [ Links ]
6. G. Bernat, A. Colin, S. M. Petters. PWCET: A tool for probabilistic Worst–Case Execution Time Analysis of Real–Time Systems. Technical Report YCS–2003–353, Department of Computer Science. University of York. UK. 2003. pp. 2–4. [ Links ]
7. J. J. Medel, P. Guevara, D. Cruz. Matricial estimation for start times with stochastic behaivor by periodic real time tasks in a concurrent system. MMACTE'05 Proceedings of the 7th WSEAS International Conference on Mathematical Methods and Computational Techniques in Electrical Engineering. UK. 2005. pp. 254–255. [ Links ]
8. H. Nyquist. ''Certain Topics in Telegraph Transmission Theory''. Proceedings of The IEEE. Vol. 90. February 2002. pp. 285–286 [ Links ]
9. J. J. Medel. ''Análisis de Dos Métodos de Estimación para Sistemas Lineales Estacionarios e Invariables en el Tiempo con Perturbaciones Correlacionales con el Estado Observable del Tipo: Una Entrada por Salida.'' Computación y Sistemas. Vol. 5. 2002. pp. 216. [ Links ]
10. P. Guevara, G. Delgado, B. del Muro. Modelado y Validación de un Vector de Tiempos de Ejecución para Tareas en Tiempo Real Concurrentes que Simulan un Motor de Corriente Continua. VIII Congreso Internacional sobre Innovación y Desarrollo Tecnológico. México. 2010. pp. 3–5. [ Links ]
11. T. Soderstrom, P. Stoica. ''On some system identification techniques for adaptive filtering.'' IEEE Trans. Circuits and Systems. Vol. CS–35. 1988. pp. 457–461. [ Links ]
12. D. B. Stewart. Measuring Execution Time and RealTime Performance. Embedded Systems Conference. Boston. 2006. pp. 2–7. [ Links ]
13. G. Delgado, P. Guevara, J. S. Falcón. Simulación Concurrente en Tiempo Real de un Motor de Corriente Continua Sobre la Plataforma QNX. XIV Congreso Latinoamericano de Control Automático, XIX Congreso de la Asociación Chilena de Control Automático ACCA. Chile. 2010. pp. 2–6. [ Links ]