Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.64 Medellín July/Sept. 2012
ARTÍCULO ORIGINAL
Distributed maximum power point tracking in photovoltaic applications: active bypass DC/DC converter
Seguimiento del punto de máxima potencia distribuida en aplicaciones fotovoltaicas: convertidor DC/DC para desviación activa
Carlos Andrés Ramos-Paja*1, Roberto Gira2, Eliana Isabel Arango Zuluaga1
1Universidad Nacional de Colombia. Carrera 80 N° 65-223. Medellín, Colombia.
2Universitat Rovira i Virgili. Avda. Paísos Catalans 26, 43007. Tarragona, España.
*Autor de correspondencia: teléfono: + 57 + 4 + 425 53 45, fax: + 57 + 4 + 234 10 02, correo electrónico: caramosp@unal.edu.co (C. Ramos)
(Recibido el 10 de enero de 2012. Aceptado el 28 de agosto de 2012)
Abstract
An active bypass structure is proposed to maximize the power production in photovoltaic modules under mismatched conditions. Its efficiency is compared with single and distributed maximum power point tracking solutions based on conventional DC/DC structures. The analysis and simulations performed under realistic assumptions demonstrate the benefits of the novel active bypass converter over solutions based on Boost, Buck or Buck-Boost converters.
Keywords: Active bypass, efficiency, distributed maximum power point tracking
Resumen
Se propone una estructura de desvío activo para maximizar la producción de potencia en sistemas fotovoltaicos bajo condiciones irregulares de operación, comparando su eficiencia con soluciones individuales y distribuidas basadas en convertidores DC/DC convencionales. Los análisis y simulaciones realistas demuestran las ventajas del nuevo convertidor de desvío activo sobre soluciones basadas en convertidores Boost, Buck y Buck-Boost.
Palabras clave: Desviación activa, eficiencia, seguimiento de punto de máxima potencia
Introduction
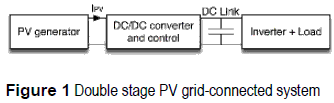
To improve photovoltaic (PV) generation systems, multiple regulation strategies able to find the optimal PV operating conditions for different solar irradiance and ambient temperature have been proposed, named Maximum Power Point Tracking (MPPT) algorithms [1]. Similarly, circuital structures to mitigate the power reduction caused by mismatching in the PV panels due to shadowing, clouding or modules tolerances, have been designed [2], Such solutions have been developed to address both stand-alone and grid- connected applications using DC/DC switching converters. In stand-alone applications the DC/ DC converter is used to adapt the PV power to the load requirements, while in grid-connected applications there are two typical approaches [2]: single-stage and double-stage (DS) inverters. In the DS structures, which block diagram is presented in figure 1, the PV power is optimized by means of a DC/DC converter, and a DC-link transfers the PV power to the grid-connected or stand-alone inverter.
In addition, many solutions to overcome the problems of power and voltage reduction caused by PV module mismatching connected to a centralized inverter have been addressed by splitting the PV generator in smaller subfields. In this context, each PV module is associated with either its own MPPT capable DC/AC micro-inverter or DC/DC converter [3], then both solutions coexist, at module level, with the classical diodes that avoid hot spots by bypassing smaller groups of cells in series. The adoption of a dedicated DC/DC converter for each PV panel is known as Distributed Maximum Power Point Tracking (DMPPT) [1], where each PV panel is driven to its optimal operating point. Moreover, almost all grid-connected DS solutions use a DC/AC inverter with a built-in regulation of the DC- link since it is a commercial standard [4].
This paper is based on the works ''Minimizing the effects of shadowing in a PV module by means of active voltage sharing'' and ''PV field distributed maximum power point tracking by means of an active bypass converter', developed by the authors, which appeared in the IEEE International Conference on Industrial Technology (ICIT-2010, © 2010 IEEE) and in the International Conference on Clean Electrical Power (ICCEP-2011, © 2011 IEEE), respectively. This paper proposes a new active-bypass solution (AB) to maximize the power extracted from PV panels at a module granularity level [3], [5], The proposed AB structure uses a parallel-like connection instead of the cascade, series-like, connection of typical DMPPT solutions [3], therefore the AB circuit requires one inductor less than DMPPT based on Boost, Buck or Buck-Boost converters. This structural difference is also important in terms of efficiency since lower losses are present.
To provide comparison with solutions based on single MPPT traditional interfaces, the efficiencies of MPPT approaches based on typical DC/DC converters are analyzed. In addition, an overview on the basic topics related to PV generation systems and the mismatching phenomenon is given, and the basic concepts on DMPPT systems are also discussed. Moreover, the novel AB solution is analyzed in terms of efficiency and DMPPT capability, validating the proposed circuit and control algorithm by means of detailed and realistic simulations based on experimentally validated PV models. Finally, the conclusions of the work are given.
Typical DC/DC converters for maximum power point tracking
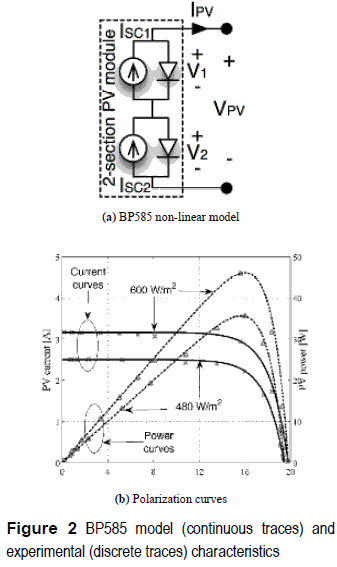
A PV panel can be modeled by using the non–linear approach given in [5], where the PV effect is represented by its electrical equivalent. Figure 2(a) shows the model of a BP585 PV panel.
From the model of figure 2(a) it is noted that the BP585, as several commercial PV panels, is composed by two PV modules in series to reduce the effect of shadows in the power production, where both modules have almost identical characteristics. Figure 2(b) shows the experimental electrical characteristics of a BP5 85 operating at 35 °C and at two different irradiance conditions: Seml = 600 W/m2 and Sem2 = 480 W/m2. Moreover, the model reported in figure 2(a), and given in (1), was parameterized to reproduce the PV panel experimental behavior, obtaining the model parameters Am = 10-5 A and Bm = 0.32 V-1. The short-circuit current Isc depends on the irradiance conditions: for Seml, ISC = 3.16 A, and for Sem2, ISC = 2.5 A. Figure 2(b) also presents the model polarization curves as continuous traces, it validating the model accuracy.
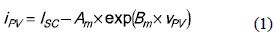
In the experiments, the PV open-circuit voltage VOC is near to 19 V, and the optimal operating point (MPP), where the maximum PV power is produced, is characterized for a PV voltage between 15 V and 16 V, named VMPP. Moreover, the PV current at the MPP is named IMPP.
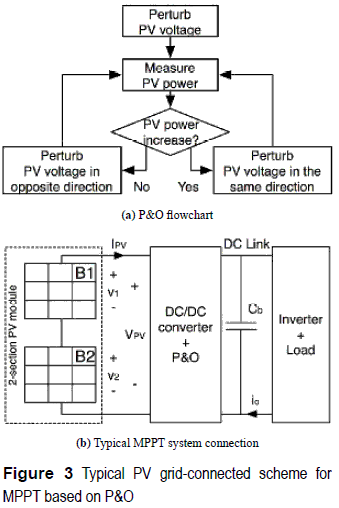
There are several MPPT strategies to find the MPP [1], where the most adopted one concerns the Perturb and Observe (P&O) technique [2], which modifies the PV voltage in the direction that generates a positive change in the PV power. The P&O flowchart is given in figure 3(a) [1].
In addition, figure 3(b) describes the classical scheme for grid-connected PV applications [2] where the DC/DC converter is regulated by means of the P&O algorithm [1, 2, 4].
An important condition to select the DC/DC converter in figure 3(b) is the desired DC- link voltage at the input of the inverter, which regulates the voltage Vb of the bulk capacitor Cb. In this way, typical Boost, Buck, and Buck-Boost topologies are widely adopted, but the output voltage of a PV system based on such converters is not the same. Such a condition can be addressed by a proper selection of the inverter, e.g. Buck, Boost, or Buck-Boost inverter. Moreover, a structural reorganization of the PV array can be used to achieve a desired inverter input voltage.
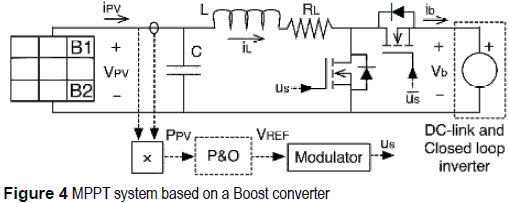
MPPT based on a Boost converter
The electrical scheme of the Boost converter based MPPT approach is depicted in figure 4, where a synchronous configuration has been adopted since it provides a higher efficiency than the classical Boost. Such a circuit models the closed-loop inverter by a voltage source, and the parasitic resistances of the inductor and MOSFETs have been collected into the RL resistor [6].
From the steady-state analysis of figure 4 circuit, and considering the PV panel operating at its MPP, VPV = VMPP, and IPV=I MPP, the inductor current iL is given by IBO = IMPP, and the duty cycle DBO required to operate in such MPP considering a regulated DC-link voltage Vb is
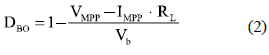
Then, the power losses on this Boost MPPT approach at the PV panel MPP is calculated as
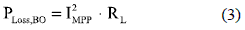
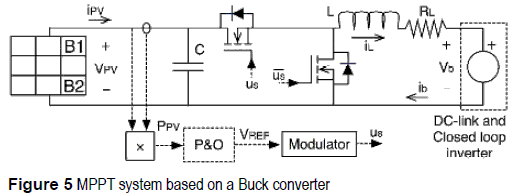
MPPT based on a Buck converter
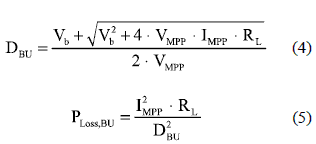
The Buck converter based MPPT approach is depicted in figure 5, where again a synchronous configuration has been adopted with a single RL resistor. From its circuital steady-state analysis, the inductor current is IBU = IMPP /DBU, and the duty cycle and power losses at the MPP for this Buck based MPPT approach are given by (4) and (5), respectively.
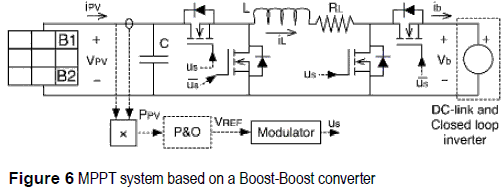
MPPT based on a Buck-Boost converter
The Buck-Boost converter based MPPT approach, based on a non-inverting synchronous configuration, is depicted in figure 6. From its steady-state analysis, the inductor current at the MPP is IBB = IMPP/DBB, while the duty cycle DBB and power losses PLOSS,BB are:
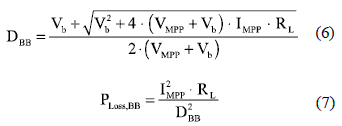
Efficiency comparison and considerations
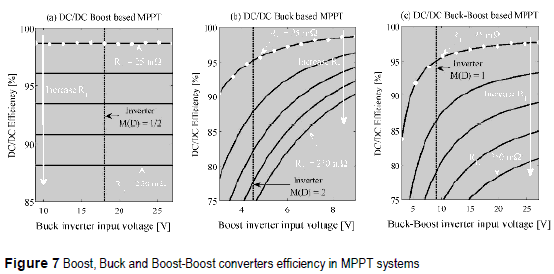
Considering a BP585 half module with ISC = 5 A, VOC = 11 05 V, VMPP = 9 V, IMPP = 4. 72 A maximum power PMPP, = 42.48 W, and a realistic RL within [25, 250] mΩ, the efficiencies of the Boost, Buck and Buck-boost PV interfaces are depicted in figure 7(a), 7(b) and 7(c), respectively.
Since figure 7 analyses consider different DC- link voltages, different inverters must be adopted to provide the same grid voltage: in the Boost based MPPT a Buck inverter [4] is required, in the Buck based MPPT a Boost inverter is required [7], and in the Buck-Boost based MPPT a Buck-Boost inverter is needed [8]. To illustrate the analyses, 9 V peak-output voltage inverters are considered: for the Buck inverter it implies an input-output voltage relation M(D) = 1/2, or a duty cycle of 50 %; in the Buck inverter M(D) = 2 corresponds to the same duty cycle; and in Buck-Boost PWM inverters a duty cycle of 50 % represents M(D) = 1. Therefore, the adopted DC/DC converters operating with the selected inverters are equivalent systems.
Figure 7 analyses show that the efficiencies of the Buck and Buck-Boost solutions depend on the adopted DC-link voltage, while the Boost solution has an almost constant efficiency. From such curves it is also concluded that the Boost solution is the most efficient one. To analytically verify such an hypothesis, the solutions power losses are normalized for the PMPP = IMPP .VMPP to define the losses factor β = PLOSS/PMPP for the Boost βBO Buck βBU and Buck-boost βBB cases
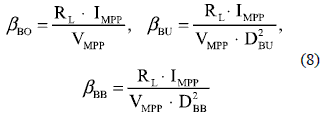
Where βBO < βBU and βBO < βBB for the same condition because DBU < 1 and DBB < 1, which confirms that the Boost interface is the most efficient. Similarly, at the same DC-link voltage DBU > DBB whlch leads to βBU < βBB.
Mismatching phenomenon and distributed MPPT
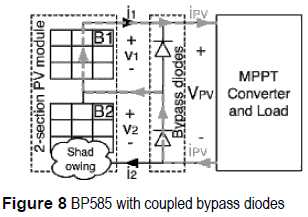
In the experiments and simulations of figure 2(b) both PV modules exhibit the same irradiance conditions, but in real applications some PV modules can be shaded [5] by external objects generating different short-circuit currents. This phenomenon, named Mismatching, can produce hot spots that degrade the PV panel, and commercial PV manufactures include bypassing diodes to reduce such effect [3], In example, the BP585 has two bypass diodes as depicted in figure 8, and if a PV module is shaded, the associated diode is activated for i1 > ISC1 or i2 > ISC2.
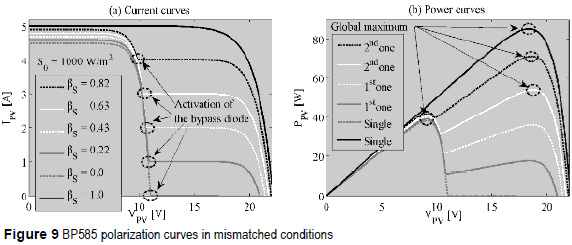
Figure 9 presents the BP585 simulation for multiple mismatching conditions: a reference irradiance S0 = 1000 W/m2 was adopted, and the irradiance of the first and second modules, SM1 and SM2, is given by the irradiance ratio βS = SM1/SM2, where SM1 = KS1 . S0 and SM2 = KS2. S0 with KS1 = [0.98, 0.96, 0.94, 0.92, 0.90, 1.00] and KS2 = [0.80, 0.60, 0.40, 0.20, 0.00, 1.00].
It is noted that the first module exhibits a higher irradiance than the second one, which is eventually bypassed. Figure 9(a) also presents the activation of the second bypass diode when i2 > ISC2, producing power curves with two maximum points [3, 5], In uniform conditions, βS = 1, or with a module totally shaded, βS = 0, the PV panel exhibits a single maximum. Moreover, the global maximum could be at the first or second peak depending on βS, which could confuse the P&O controller. In addition, since the shaded PV module could be bypassed, there is not possible to extract the maximum achievable power PDMPP represented by the sum of the modules PMPP.
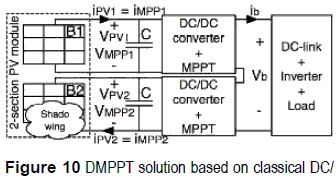
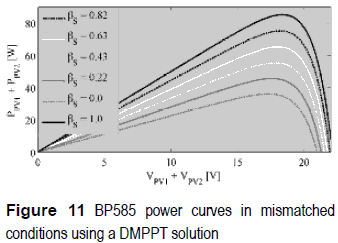
To obtain the PDMPP each PV module can be associated to a DC/DC converter to extract all the PMPP. Such a solution is known as Distributed Maximum Power Point Tracking or DMPPT [3]. Figure 10 describes the structure of a DMPPT solution based on classical DC/DC converters, where the DC/DC converters outputs are connected in series, but it is also possible to connect the converters outputs in parallel [5]. Figure 11 shows simulations on the same conditions of figure 9 but adopting a DMPPT solution, where a single maximum exists since there are no bypass diodes. Therefore, the DMPPT approach permits to extract the PDMPP but the adopted DC/DC converters impact the output power since Boost, Buck, and Buck-Boost exhibit different losses.
The mismatching effect on the adopted two- module PV array can be also modeled by the difference between the modules MPP currents IMPP1 and IMPP2, which can be related through a current factor ki = IMPP2/ IMPP1. Such a factor represents the level of mismatching between the two modules that is constrained within 0 ≤ ki ≤ 1, where ki = 0 corresponds to a single module totally shaded, while ki = 1 corresponds to uniform conditions. The power losses in the Boost PLOSS,BO2M, Buck PLOSS,BU2M and Buck-Boost PLOSS,BB2M DMPPT solutions, under mismatching conditions characterized by ki and Ø= RL. IMPP12, are given by
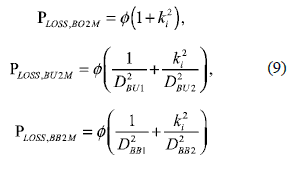
and the derivative of such power losses depending on the ki are
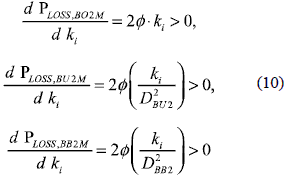
Where PLOSS,BO2M, PLOSS,BU2M and PLOSS,BB2M are monotonically increasing functions, which means that the losses increase when the level of mismatching decrease, therefore the lower losses occur at ki = 0, i.e. one module shaded; and the higher losses occur at ki = 1, i.e. uniform conditions.
The efficiency comparison is analyzed by means of the losses factor β, which in this case depends on both power converters losses, PLOSS,2M = PLOSS1 + PLOSS2, and on the total power generated by the array, PMPP,2M = PMPP1 + PMPP2. To simplify the expressions, the MPP voltages of both PV modules are considered equal, VMPP1 ≈ VMPP2 ≈ VMPP, which is an acceptable approximation as reported in figure 9(b). The losses factor for the DMPPT based on two Boost βBO2M, two Buck βBU2M, and two Buck-Boost converters βBB2M, are given in (11).
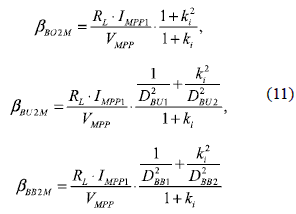
It is noted that the Boost based DMPPT is the most efficient solution for any operating condition:
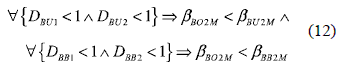
Finally, in mismatching conditions the DMPPT is more efficient than the classical bypass diodes solution, and in uniform conditions the bypass diodes solution is the more efficient since it does not introduce power losses while the DMPPT solution introduces its maximum power losses.
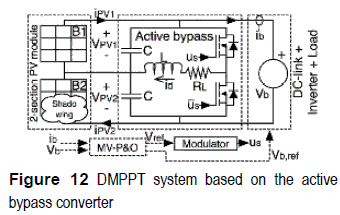
Active bypass converter
The proposed active bypass (AB) converter is depicted in figure 12. It is based in two complementary operated MOSFETs, therefore the losses are collected in resistor RL, and the control structure is based on a multivariable P&O and a modulator. Moreover, the DC-link and closed-loop inverter are represented by a voltage source. Since the AB converter compensates the differences between the PV currents in mismatching conditions, no bypass diodes are required.
In steady-state [6], the module voltages VPV1 and VPV2, and the system output current Ib, are
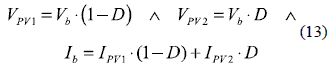
Where D corresponds to the duty cycle, Vb to the AB output voltage, and IPV1 and IPV2 represent the modules currents. From equation (1), the PV module currents are given by IPV1 = ISC1 – A1 . exp (B1. VPV1) and IPV2 = ISC2 - A2 .exp(B2 . VPV2), and the AB output current is calculated as
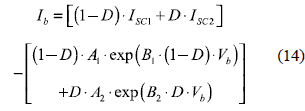
The power delivered by the AB is Pb = Vb. Tb, where the second partial derivative of Pb is
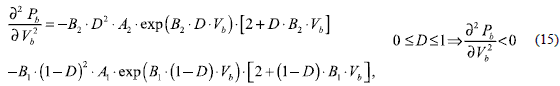
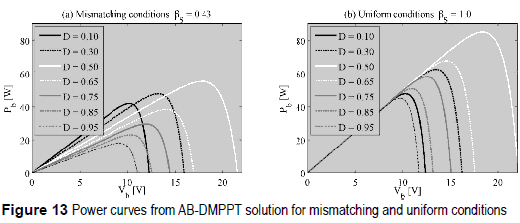
From (15) is it noted that the AB power-voltage curve exhibits a negative concavity for any duty cycle D, therefore there is always a single maximum that an external MPPT controller is able to track. This is verified in figure 13, where uniform and mismatched conditions are considered, and optimum Vb and D values exist. Such a condition requires a multivariable P&O.
AB converter regulation by means of a Multivariable P&O
It is noted that the AB converter duty cycle defines the difference between the PV voltages (13), i.e. VPV1 - VPV2, then to define both PV voltages it is also necessary to set Vb, i.e. VPV1 + VPV2. Therefore, both D and Vb must be optimized as reported in figure 13.
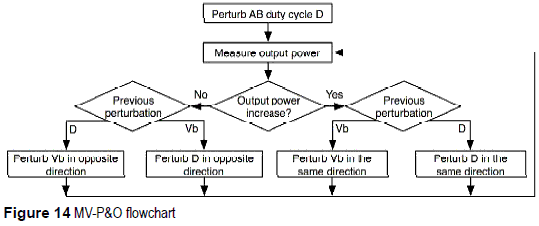
From figure 12 it is noted that the AB converter introduces losses due to RL. This aspect has been addressed by optimizing the output power instead of the individual modules PV powers, which provides two advantages over traditional DMPPT approaches: first, it is required a single current sensor instead of dedicated current sensors for each PV modules [3], Second, the DC/DC converter operating point is defined to produce lower power losses. To optimize both D and Vb, the multivariable P&O (MV-P&O) algorithm given in figure 14 was adopted, which perturbs one variable, i.e. D or Vb, and observes the perturbation effect on the output power.Efficiency of the DMPPT based on the AB converter
From the steady state analysis of the AB converter of figure 12, the inductor current Id is given by (16) if the MPP is ensured in both PV modules, while Vb fulfills the Kirchhoff law.
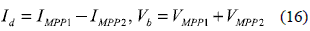
Since grid-connected inverters normally provide a Vb controller Gv, the condition given in (16) is achieved by generating Gv reference by means of MV-P&O, where the MV-P&O optimizes Vb.
To operate the AB on the MPP for both PV modules, AB duty cycle is given by (17), and the associated AB power losses are given in (18).
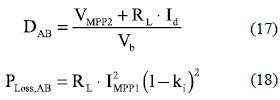
Since in the AB solution the inductor current is lower or equal than in the Boost case, a similar RL is considered for the analysis. The derivative of (18) is given by
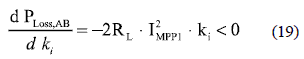
which implies that the AB power losses are given by a monotonically decreasing function, whose maximum is obtained at ki = 0 that corresponds to the minimum losses in the Boost case for the same conditions (9)-(10). The minimum losses in the AB converter are obtained at ki = 1 condition, being near to zero. From (18) and (19) it is noted that the AB solution provides a trade-off between bypass diodes and classical DMPPT approaches: in mismatching conditions, i.e. 0 ≤ ki ≤ 1, the AB solution allows to track the global MPP as in the DMPPT; while in uniform conditions, i.e. ki = 1, the AB system does not introduce power losses as the bypass diodes.
The efficiency comparison of the AB based DMPPT with the classical DMPPT is performed by means of the losses factor βAB2M, which in this case depends on the AB power losses, PLoss,AB, and on PMPP,2M = PMPP1 + PMPP2. To provide a fair comparison, the MPP voltages of both PV modules have been considered equal, obtaining the βAB2M in (20), which is always smaller than the Boost DMPPT losses factor (11), i.e. ∀ ki >0 ⇒ βAB2M < βBO2M. Therefore, the AB solution is more efficient in uniform and mismatched conditions, but exhibits the same efficiency when a PV module is totally shaded. Moreover, the relative losses factor βBO,AB (20) confirms that the AB approach is more efficient than the Boost solution for any ki > 0 condition.
Antifungal bioassay
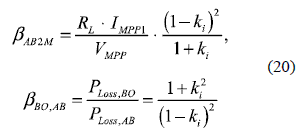
Also, since the Boost solution is the most efficient option among the traditional DMPPT, the AB solution is a general improvement. But the AB output voltage is equal to the sum of the PV voltages, therefore a Buck, Boost or Buck- Boost inverter is required to reach the grid voltage, which is similar to the bypass diodes approach.
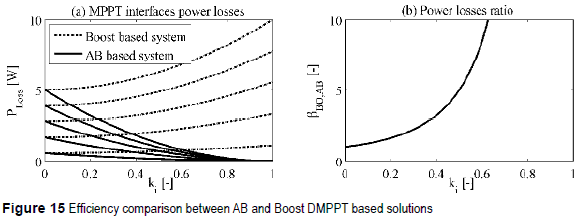
Figure 15(a) plots the analyses given in (9), (18), and (20), which confirm that the AB solution is the most efficient one. In addition, it is also observed that the AB approach does not introduce power losses in uniform conditions, i.e. ki = 1. Similarly, figure 15(b) depicts the βBO,AB behavior, where it is noted that the AB power losses are smaller than in the Boost solution. Finally, equation (20) and figure 15 demonstrate the improved efficiency of the AB based DMPPT.
Simulation results
The previous analyses have been validated by means of simulations based on realistic and non–linear circuital simulations performed in the power electronics simulator PSIM. The simulations consider BP585 modules under the mismatched conditions given in figure 9 with βS = 0.43, βS= 1.0, and βS= 0.0. The simulations include the bypass diodes solution with a P&O algorithm, a Boost based DMPPT with the MV-P&O algorithm, and the proposed AB-based DMPPT with the MV-P&O algorithm. Finally, the simulations also consider the converters dynamics.
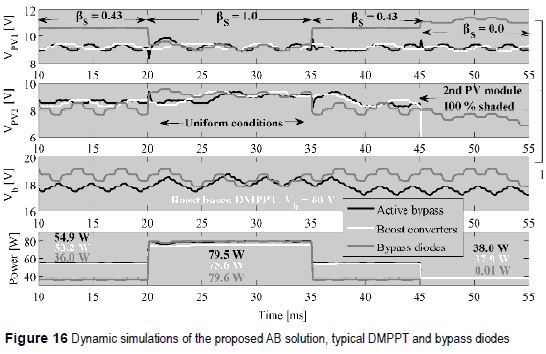
The simulations where carried out for dynamic irradiance conditions: from 10 ms to 20 ms the mismatched condition βS= 0.43 is imposed, then the uniform condition βS= 1.0 is present between 20 ms and 35 ms, returning to βS= 0.43 from 35 ms to 45 ms, and finally the second PV module is totally shadcd βS = 0.0 from 45 ms. Figure 16 shows the simulation results, where in both DMPPT solutions the PV voltage of the first module is near the MPP voltage, which corresponds to the half of VMPP reported in figure 2(b). But in such mismatched condition the bypass diodes operates at the second peak of the power-voltage curve of figure 9, imposing a large voltage. Similarly, the voltage of the second PV module reports that the three solutions follow the VMPP. But from 45 ms, when the second PV module is totally shaded, the DMPPT solutions drive to zero VPV2 because such a module does not produce power, while the bypass diodes takes more time to reach such a condition, wasting energy.
Moreover, the AB converter drives Vb to its optimal value for the mismatching level, while the bypass diodes P&O drives Vb to one of the power peaks. In uniform conditions both AB and bypass diodes impose the same DC-link voltage, where Vb = VMPP1 +VMPP2 is ensured. In addition, the voltage boosting of the Boost based DMPPT is illustrated by a larger Vb.
The simulations also reportahighpowerproduction of the DMPPT solutions compared with the bypass diodes. In addition, the AB solution produces higher energy than the traditional DMPPT for any mismatched condition: at βS= 0.43 the AB delivers 3.2% more energy than the other DMPPT and 52.5 % more energy than the bypass diodes. Similarly, at βS= 1.0 the AB provides 5.2 % more energy than the typical DMPPT, while at βS = 0.0 the AB provides the same energy than the classical DMPPT. Such results confirm that the AB based DMPPT exhibits the best characteristics of both bypass diodes and classical DMPPT solutions: small losses at uniform conditions and global maximum power. Finally, for the 45 ms simulated, the AB produces 2670.6 J, while the Boost and bypass diodes solutions provide 2577 J and 1914.1 J, respectively.
Conclusions
This paper proposes an active bypass structure to perform DMPPT. In comparison with traditional bypass diodes solution, under the same mismatching conditions, the AB solution provides higher power and exhibits similar power losses at uniform conditions. It has been demonstrated that the AB system eliminates the multiple peaks condition that occurs in mismatching situations, therefore an external MPPT controller is able to reach the maximum power for any mismatching condition. Similarly, it has been demonstrated that AB based DMPPT systems produce lower power losses than solutions based on typical DC/ DC converters.
Acknowledgements
This work was supported by VECTORIAL- MPPT project of the Universidad Nacional de Colombia.
References
1. N. Femia, G. Petrone, G. Spagnuolo, M. Vitelli. ''Optimization of perturb and observe maximum power point tracking method.'' IEEE Transactions on Power Electronics. Vol. 20. 2005. pp. 963-973. [ Links ]
2. N. Femia, G. Petrone, G. Spagnuolo, M. Vitelli. ''A Technique for Improving P&O MPPT Performances of Double-Stage Grid-Connected Photovoltaic Systems.'' IEEE Transactions on Industrial Electronics. Vol. 56. 2009 pp. 4473-4482. [ Links ]
3. N. Femia, G. Lisi, G. Petrone, G. Spagnuolo, M. Vitelli. ''Distributed Maximum Power Point Tracking of Photovoltaic Arrays: Novel Approach and System Analysis.'' IEEE Transactions on Industrial Electronics. Vol. 55. 2008. pp. 2610-2621. [ Links ]
4. M. Fortunato, A. Giustiniani, G. Petrone, G. Spagnuolo, M. Vitelli. ''Maximum Power Point Tracking in a One- Cycle-Controlled Single-Stage Photovoltaic Inverter.'' IEEE Transactions on Industrial Electronics. Vol. 55. 2008. pp. 2684-2693. [ Links ]
5. G. Petrone, C. Ramos. ''Modeling of photovoltaic fields in mismatched conditions for energy yield evaluations.'' Electric Power Systems Research. Vol. 81. 2011. pp. 1003-1013. [ Links ]
6. R. Erickson, D. Maksimovic. Fundamentals of power electronics. Ed. Springer, 2nd, New York. 2001, pp. 11–50. [ Links ]
7. C. Albea, F. Gordillo, C. Canudas. ''Adaptive control design for a boost inverter''. Control Engineering Practice. Vol. 19. 2011. pp. 32-44. [ Links ]
8. C. Wang. ''A novel single-stage full-bridge buck-boost inverter.'' IEEE Transactions on Power Electronics. Vol. 19. 2004. pp. 150-159. [ Links ]