ARTÍCULO ORIGINAL

 

Topological optimization for solids under heat and mass transfer using boundary element

 

Optimización topológica de sólidos en calor y transferencia de masa utilizando los elementos de contorno

 

 

Carla Tatiana Mota Anflor^*1, Jhon Nero Vaz Goulart¹, Rogério José Marczak²

¹Universidade de Brasilia. Engenharias. Campus Gama. DF. Brasil -71405–610.

²Universidade Federal do Rio Grande do Sul Rua Sarmento Leite 425, Porto Alegre - RS - Brasil - 90430-131.

^*Autor de correspondencia: telefax: + 55 + 61 + 310 78 901, correo electrónico: anflor@unb.br (C. Mota)

 

(Recibido el 24 de mayo de 2012. Aceptado el 7 de octubre de 2012)

 

---

Abstract

The objective of this work is to present the implementation of a topological - shape sensitivity formulation in a BEM analysis for simultaneous heat and mass transfer optimization problems. The proposed approach uses a topological derivative in order to estimate the sensitivity to create a hole in the domain of the problem. Thus, it is evaluated at internal points, and the ones showing the lowest values are used to remove material by opening a circular cavity. As the iterative process evolves, the original domain has holes progressively punched out until a given stop criteria is achieved. Since the sensitivities for each of the differential equations are different, a penalization- type approach has been used to weight the sensitivities associated to each problem. This allows the imposition of distinct penalization factors for each problem, according to specified priorities. The results obtained showed good agreement with solutions available in the literature.

Keywords: Shape optimization, potential problems, boundary elements, topological derivative, mass transfer

---

Resumen

El objetivo de este trabajo es presentar la aplicación de una formulación para el análisis de sensibilidad de forma y topologia utilizando elementos de contorno en problemas de optimización involucrando transferencia simultanea de calor y masa. El enfoque propuesto usa la derivada topològica para estimar la sensibilidad a crear un agujero en el dominio de definición del problema. De este modo, la misma se evalúa en puntos internos y aquellos que presentan los valores más bajos se utilizan para eliminar material mediante la apertura de una cavidad circular. A medida que el proceso iterativo evoluciona, el dominio se modifica progresivamente con la incorporación de más agujeros hasta que se alcanza un criterio de parada determinado. Puesto que las sensibilidades de cada una de las ecuaciones diferenciales son diferentes, un enfoque tipo penalización ha sido utilizado para ponderar las sensibilidades asociadas a cada problema. Esto permite la imposición de factores de penalización distintos para cada problema, de acuerdo a prioridades especificadas. Los resultados obtenidos mostraron una buena concordancia con soluciones disponibles em la literatura.

Palabras clave: Optimización de forma, problemas potenciales, elementos de contorno, derivada topológica, transferencia de masa

---

 

 

Introduction

Materials classified as porous are widely used in many applications in the engineering field. In the last years some efforts have been done in order to increase the material efficiency in different areas. A porous medium was defined by Kaviany [1] as a mixture of a heterogeneous solid matrix with its void with fluids. As a structural material a porous media has mechanical properties such as elasticity and strength.

The term ''porous materials'' is usually reserved to materials such as fibers, ceramic, concrete and porous rock as well. This kind of material is frequently present in a wide variety of devices or components. There are numerous scientific and engineering applications for porous materials. Some examples should be listed in order to give a panoramic view of the usage of these materials. For example, for Chemical engineering this material is found in reactors and static mixers, For Civil engineering, the concrete and the aquifers [2] (which consist of sand, gravel and fractured rock) are typical examples of porous materials, for mechanical engineering a layout of heat exchangers [3] and micro channel cooling [4] also can be modeled as a porous media, for biomedical engineering a good example are the bones, lungs and kidneys. In Dondero et al. [5] a numerical methodology for the computation of the effective thermal conductivity (ETC) of random micro-heterogeneous materials using representative volume elements and the Fast Multipole Boundary Element Method (FMBEM) was introduced. This methodology was applied to solve a two-dimensional foam–like microstructure consisting of a random distribution of circular isolated holes. The final results showed that the proposed numerical methodology is effective for the computation of the ETC of random micro heterogeneous materials.

Obviously there are many others applications which are impossible to be cited herein. With this brief review was possible to expose the extension of the problems that involves the porous materials. In this sense the main objective of this work is focused in presenting a numerical methodology to combine heat and mass transfer designs in a resulting optimal solid shape for both problems. Materials which are in charge of transferring heat and mass simultaneously should be classified as porous materials. A strategy of compromise [6] that attributes weights to the respective equations will be employed in order to establish a relationship between both problems. A well-known topological derivative (D_T) approach [7, 8] was used to evaluate the sensitivities, as an alternative to the traditional homogenization methods [9]. The boundary element method (BEM) was chosen to provide the numerical solution. Since the BEM does not require domain meshes, a significant reduction in the computational cost during the iterative optimization process can be achieved, in comparison to other traditional numerical methods. As the efforts will be straight to the solution of multi-objective optimization problems using the proposed methodology, this work will be structured as: Firstly, the D_T formulation for the Poisson equation is presented. Next, the optimization procedure employed herein for multi-criteria problems detailed. In order to access the formulation, a case of simultaneous two-dimensional heat and mass transfer is optimized for mass reduction and discussed.

 

Topological derivative

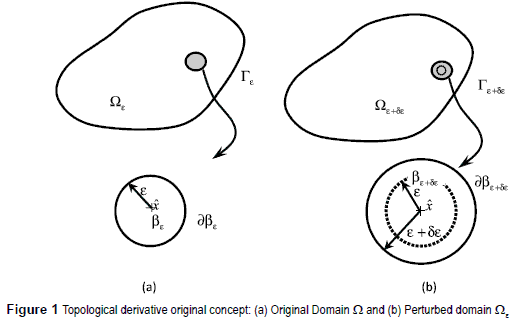
A topological derivative for Poisson Equation is applied in this work. A simple example of applicability consists in a case where a small hole of radius (ε) is open inside the domain. The concept of topological derivative consists in to determine the sensitivity of a given function cost (Ψ) when this small hole is increased or decreased (figure 1).

The local value of D_T at a point (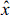) inside the domain for this case is evaluated by:

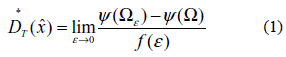
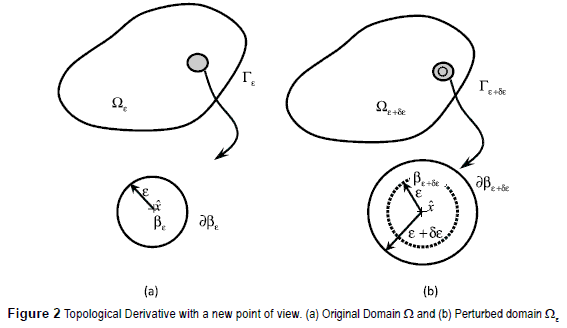
Where Ψ(Ω) and Ψ(ε) are the cost function evaluated for the original and the perturbed domain, respectively, and f  is a problem dependent regularizing function. By equation (1) it is not possible to establish an isomorphism between domains with different topologies. This equation was modified introducing a mathematical idea that the creation of hole can be accomplished by single perturbing an existing one whose radius tends to zero, figure 2.

This allows the restatement of the problem in such a way that it is possible to establish a mapping between each other [10].

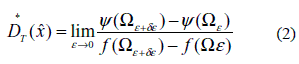
Where δε is a small perturbation on the holes's radius. Equation (2) gives a shape sensitivity when the hole increase or decrease. It is also important to notice the both Eq. 1 e Eq. 2 are equivalent, as presented in [10].

The D_T for the steady state heat transfer will be briefly reviewed herein. In the case of linear heat transfer, the direct problem is stated as:

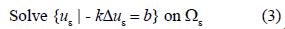
Subjected to

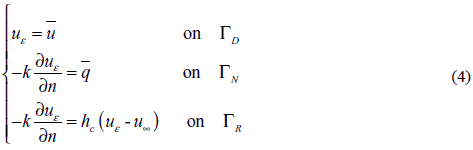
where

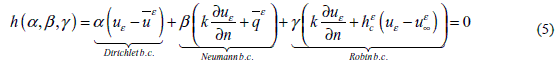
Is a function which takes into account the type of boundary condition on the holes to be created 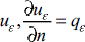are the temperature and flux on the hole boundary, while u^ε_∞ and h_^εcare the hole's internal convection parameters, respectively).

Taking a general form for a cost function written as

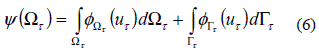
Where τ is a parameter associate to the shape change velocity, i.e., x_τ (x) = x + τv (x). The sensitivity of the cost function with respect to τ can be derived from the Gâteaux derivative.

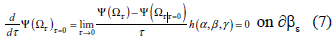
Therefore the problem should be re-stated as:

Evaluate: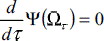

Subject to

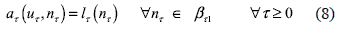
Where a is α_τ continuous, coercive bilinear form, l_τ is a continuous linear functional and β_τ is the space of the admissible perturbation functions for the perturbed domain Ω_τ. Using the total potential energy as a cost function 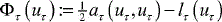the α_τ and l_τ functional are written as:

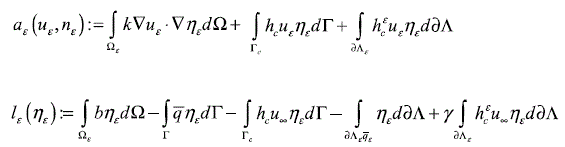
Considering Eq. (8) one can derive the D_T expression particularized for the three classical boundary conditions prescribed on the holes.

 

Neumann boundary condition

For this case the eq. (5) is particularized as (α = 0, β=1, γ =0) and the D_T is obtained by taking the limit:

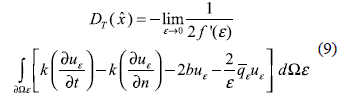
where t and n are the tangential and normal directions respectively.

Both cases of Neumann boundary conditions must be considered:

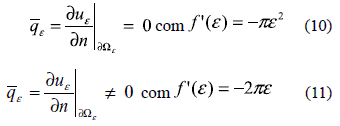
For homogeneous and non-homogeneous cases respectively.

Dirichlet boundary condition

For this case the eq. (5) is particularized as (α = 1, β=0, γ =0) and the D_T is obtained by taking the limit:

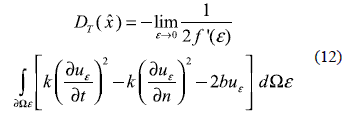
Being the conditions

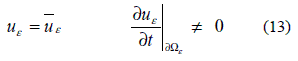
Used along with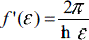

Robin boundary condition

In this case one has (α = 0, β=0, γ =1)  and the D_T is obtained by taking the limit:

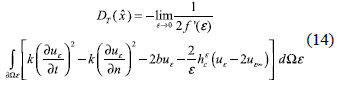
Now the regularizing function for this case is f'(ε)=-2πε.

Afterwards table 1 summarizes the final expressions for topological derivative, after apply the respective regularizing function for each boundary condition, under consideration in Eq. (9), Eq. (12) and Eq. (14). It is also important to inform that the same formulas presented as table 1 are used for determining the sensitivity of a domain governed by the Laplace equation.

It is also important to take attention that D_T is evaluated by different expressions for interior and boundary points. Another remark relies on the fact that the expressions presented as tab. 1 are deduced taking the total potential energy as cost function.

 

Multi-criteria optimization procedure

The optimization of problems under more than one cost function is becoming quite common in engineering practice. For instance, in the electronic industry the miniaturization of components are leading to excessively slender designs, which demands new and efficient cooling devices, usually base on porous media. The successful design of such components imply in the optimization of both, heat and mass transfer. This technology presents two basic advantages [11]: (a) the porous heat sink provides more than 10 times the contact area of a smooth surface; and (b) the irregular structures of the porous heat sinks, at sufficient high velocities, causes irregular fluid flow, increasing the thermal dispersion conductivity. This is a typical case where the heat conduction would lead to an optimum design, while the convection would lead to another one. Therefore, it is necessary to combine both optimization problems in a single one. Clearly, the adoption of one (single criteria) design could result in a less efficient performance of the product from the other criteria(s) point(s) of view.

In engineering design practice, it is usual for a thermal solid to be required to satisfy one of the following optimality criteria:

A   As uniform mass transfer rate as possible;

B   As uniform heat transfer rate as possible;

C   Maximum possible efficiency in both criteria A e B, simultaneously.

From the optimization point of view, the first two criteria mean the extremization of a single objective function. The satisfaction of criterion C needs the satisfaction of multiple design criteria, which is the goal of this work. After separate BEM heat and mass analysis, the heat flux and mass densities are determined at internal points. These values are used to evaluate the topological derivative. In order to estimate the relative material usage efficiencies at an internal point, two dimensionless factors are introduced as:

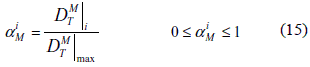
where αⁱ_M  is the mass flux efficiency factor, 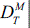_i is the mass flux topological derivative at internal point i, and 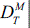_max is maximum value of 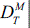_i. A heat flux efficiency factor αⁱ_H is derived accordingly. During the optimization process the basic goal is to remove material where if is less efficient. However, it may happen that for multi- criteria optimization (C), internal points with low heat fluxes does not necessarily will have low mass fluxes. In such cases it is necessary to apply a strategy to generate a compromise between both phenomena. Rosvany et al. [6] proposed a strategy of compromise in terms of weighted sums of αⁱ_H and αⁱ_M :

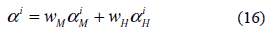
Where w_H and w_M are the weighting factors for the heat and the mass problems respectively. It is important to note that

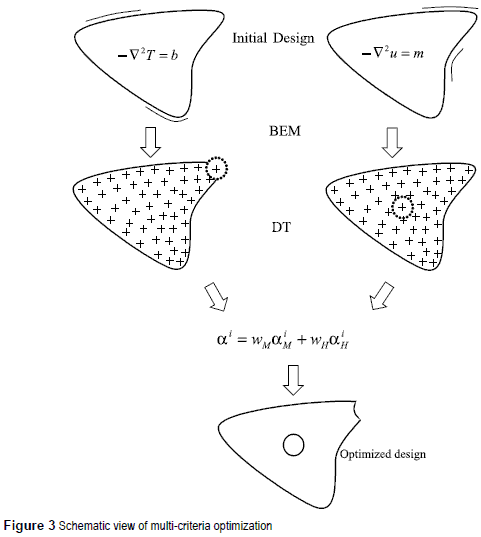
The weighting factors provide a meaningful way of assigning different levels of importance to each problem. Therefore, when w_M= 1 and w_H= 0 the criteria A is obtained as a special case, while w_M= 0 and w_H=1 reduces the problem to a simple mass transfer optimization (criteria B). Figure 3 depicts a scheme in order to illustrate the multi-criteria optimization procedure.

 

Numerical example

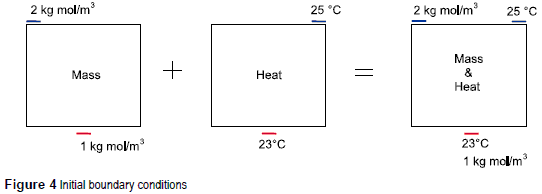
The algorithm used in this work, for performing the numerical calculations, was developed using Matlab. This algorithm is composed by the subroutines: BEM (solver), D_T (sensitivity and geometric removal material) and multi- criteria procedure, as well. Using this algorithm, a porous square domain of dimension 20 ' 20 is submitted to simultaneous heat and mass transfer. The geometry is discretised with 40 boundary elements integrated with 6 Gauss points. The linear discontinuous elements will be adopted due the irregular boundaries resulted from the optimization process. The boundary conditions are depicted in figure 4. The heat transfer problem has a high temperature of 25°C at the right upper comer and a low temperature of 23°C at the mid lower side. The mass transfer problem has a high potential of 2 kg mol/m³ on the upper left corner and a low potential of 1 kg mol/m³ on the mid lower side. The remaining boundary is insulated, as well as all the holes open during the process. The conductivity and diffusivity coefficient are set as 1W/m°C and 1 m²/s, respectively. A regularly spaced grid of internal points was automatically generated, taking into account the radius of the holes created during each iteration. The radius was taken as a fraction of a reference dimension of the domain (r = αl_ref)). Usually l_ref = min(height, width) was adopted. The objective in all cases is to minimize the material volume. The current volume of the domain (A_f) was checked at the end of each iteration until a reference value is achieved (A_f = βA₀, where A₀ represents the initial volume). This numerical example will be studied with α_M = 0.4 and α_H = 0.6, to illustrate a case where a higher priority is imposed to one of the problems. The values of αM and αH should be adjusted according to the priority set by the designer. Three internal control points were chosen in order to check temperature, mass concentration, heat and mass flux as the process evolves.

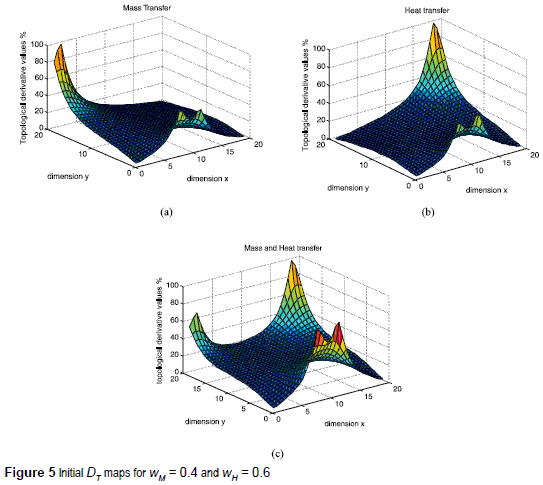
Fig. 5 illustrates the behavior of the topological derivative values calculated for mass (figure 5a) and heat transfer (figure 5b) inside the domain before the optimization process be initialized. Figure 5c represents the topological derivatives values for both problems obtained by equation (7).

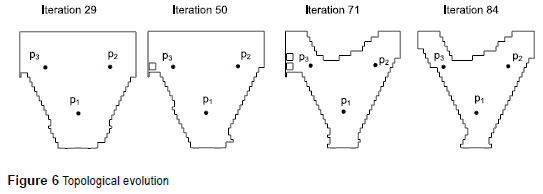
Figure 6 depicts the topology evolution during the iterative process. It is clear the material removal where it is less necessary, according to the weighting factors used. The process iteration was halted when a remaining volume of 50 % was achieved. As explained before, three internal points of control were chosen (p₁(10,6), p₂(4.4,14) and p₃ (15.6,14)), to account the internal physical parameters. A mean of the temperature and mass of the boundary elements were considered too.

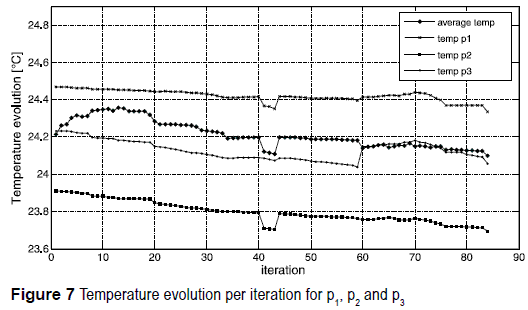
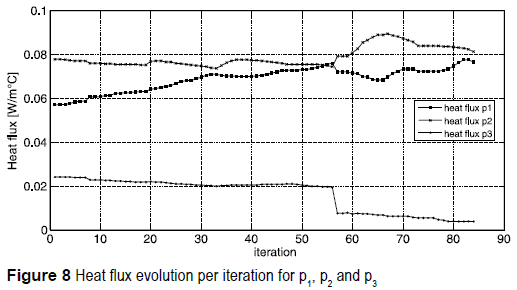
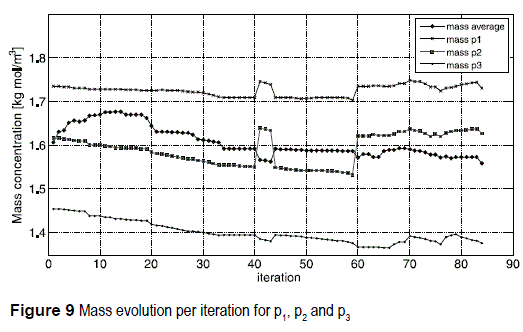
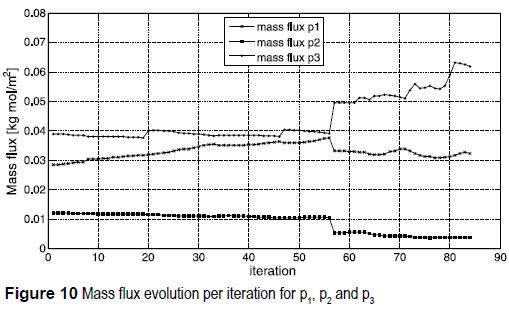
Figure 7 and 8 show the history of temperature and heat flux at the three internal points. Analyzing the heat flux graph, it is possible to verify that the gradient at the points p₁ and p₂ are increasing as the process evolves, while at point p₃ there is a visible decrease of the gradient value. In figure 7, the point p₃ shows an increase of temperature due to the decrease of the gradient at that location. It is evident that the region which presents less efficiency is being removed. Consequently, the flux is maximized along the path connecting the points P₁ and p₂. figure 9 and 10 depict the history of mass concentration and mass flux at the three internal points. The mass flux at the point p₁ and p₂ drops after iteration 56, while it simultaneously increases at the point p₃. This occurs because after iteration 56 the D_T values at the internal points are gradually homogenized, making difficult to select locations with conspicuous lower values. The final geometry resulted in asymmetric Y-shaped design, with material concentrated at the right hand side, due to the weighting factors imposed. However, the mass flux is maximized from the point p₁ to p₃.

 

Conclusions

The goal of this work was to extend the application of topological-shape sensitivity analysis to optimization problems governed simultaneously by two different equations, i.e., heat and mass transfer. In order to achieve this, a compromise optimization scheme was used, relying on topological derivative results for the problem. The BEM was used to provide the numerical solution. It is important to point out that D_T has the potential total energy as an implicit cost function. Therefore, the regions which store energy less efficiency are progressively removed. The final topology obtained for the numerical case showed the weighting factors influence for both problems (mass or heat transfer). It was shown that the present methodology can deliver optimal designs of solids in problems submitted to multi-criteria. It is also interesting to note the importance in specifying the priorities for both problems in order to reach physically meaningful solutions for materials porous.

 

References

1. A. Kaviany. Principle of Heat Transfer in Porous Media. Ed. Springer - Verlag. New York. 1991. pp. 1-153.         [ Links ]

2. A. Mantoglou, M. Papantoniou, P. Giannoulopoulos. ''Management of coastal aquifers based on nonlinear optimization and evolutionary algorithms''. Journal of Hydrology. Vol. 297. 2004. pp. 209-228.         [ Links ]

3. B. Boyd, K. Hooman. ''Air-cooled micro-porous heat exchangers for thermal management of fuel cells''. International Communications in Heat and Mass Transfer. Vol. 39. 2012. pp. 363-367.         [ Links ]

4. S. Ndao, Y. Peles, M. Jensen. ''Multi-objective thermal design optimization and comparative analysis of electronics cooling technologies''. International Journal of Heat and Mass Transfer. Vol. 52. 2009. pp. 4317-4326.         [ Links ]

5. M. Dondero, A. Cisilino, J. Carella, J. Tomba. ''Effective thermal conductivity of functionally graded random micro-heterogeneous materials using representative volume element and BEM''. International Journal of Heat and Mass Transfer. Vol. 54. 2011. pp. 3874-3881.         [ Links ]

6. G. Rozvany, O. Sigmund, T. Birker. ''Optimal Design of Composite and Fibre Reinforced Plates''. Optimal Design with advanced materials. Vol. 23. 1993. pp. 293-309.         [ Links ]

7. J. Cea, S. Garreau, P. Guillaume, M. Masmoudi. ''The shape and topological optimizations connection''. Comput Methods Appl. Mech. Engrg. Vol. 188. 2000. pp. 713-726.         [ Links ]

8. J. Sokolowski, A. Zochowski. ''Topological derivatives of shape functional for elasticity systems''. Mech. Struct. Mach. Vol. 29. 2001. pp. 331-349.         [ Links ]

9. P. Bendsoe, N. Kikuchi. ''Generating optimal topologies in structural design using a homogenization method''. Comput. Methods Appl. Mech. Engrg. Vol. 71. 1988. pp. 197-224.         [ Links ]

10. A. Novotny, R. Feijóo, E. Taroco, C. Padra. ''Topological-shape sensitivity analysis''. Comput. Methods Appl. Mech. Engrg. Vol. 192. 2003. pp. 803–829.         [ Links ]

11. T. Jeng, S. Tzeng, Y. Hung. ''An analytical study of local thermal equilibrium in porous heat sinks using thin theory''. International Journal of Heat and Mass Transfer. Vol. 49. 2006. pp. 1907-1914.         [ Links ]