ARTÍCULO ORIGINAL

 

Análisis del comportamiento dinámico de un vehículo con suspensión independiente tipo paralelogramo deformable y barras de estabilidad transversal

 

Analysis of the dynamic behavior of a vehicle with fully independent double-wishbone suspension and anti-roll bars

 

 

Gonzalo Rojas, Nelson Arzola^*

Research Group OPTIMUN, Department of Mechanical and Mechatronics Engineering, National University of Colombia. Bogotá, D.C., Colombia.

^*Autor de correspondencia: teléfono: + 57 + 1 + 316 5000, ext. 14 062, fax: + 57 + 1 + 316 5333, correo electrónico: narzola@unal.edu.co (N. Arzola)

 

(Recibido el 27 de agosto de 2012. Aceptado el 26 de abril de 2013)

 

 

---

Resumen

El artículo presenta un modelo que permite analizar la dinámica de un vehículo con suspensión independiente en las cuatro ruedas y barra de estabilidad transversal en cada eje. El modelo es programado bajo el ambiente Simulink^®Matlab^® y es útil para describir el comportamiento dinámico del vehículo usando para ello siete grados de libertad. En el trabajo se consideran los desplazamientos en el eje vertical y las rotaciones en los planos longitudinal y transversal del vehículo, para condiciones de conducción a través de una vía con irregularidades (escalones, pavimento ondulado y rampas inclinadas), giro, frenado, arranque, y combinaciones de las anteriores condiciones. Como resultados principales del modelo desarrollado se obtiene el comportamiento cinemático del vehículo bajo maniobras de conducción (ángulo de cabeceo, ángulo de inclinación transversal y aceleraciones); además, se determinan las fuerzas ejercidas por los componentes del sistema de suspensión, las transferencias de carga que ocurren entre los neumáticos debido a maniobras y las aceleraciones experimentadas por el ocupante durante la conducción del vehículo.

Palabras clave: Dinámica de vehículo, suspensión de paralelogramos deformables, barra estabilizadora transversal, maniobrabilidad, estabilidad

---

Abstract

The paper presents a model to analyze the dynamics of a vehicle with fully independent double-wishbone suspension and anti-roll bar on each axis. The model is programmed in Simulink^®Matlab^® environment and it is useful to describe the dynamic behavior of the vehicle using for that seven degrees of freedom. In the work we consider the displacements on the vertical axis and rotations at the pitch and roll planes of the vehicle for driving conditions across a road with irregularities (steps, undulating road and inclined ramp), steering, braking, starting, and combinations ofthe preceding conditions. The main results of the model developed are the kinematic behavior of the vehicle under driving transient conditions (pitch angle, roll angle, and accelerations); furthermore, it is found the forces exerted by the suspension system components, the load transfers that occur between the tires due to maneuvers and the accelerations experienced by the occupant of the vehicle while driving.

Keywords: Dynamic of vehicles, double-wishbone suspension, anti-roll bar, manoeuvrability, stability

---

 

 

Introducción

La simulación de la dinámica vehicular tuvo sus comienzos hace más de seis décadas atrás. Inicialmente se empleaban modelos simplificados para velocidades o razones de giro constantes; luego se desarrollaron modelos especializados en movimientos que empleaban sistemas de ecuaciones de diferente nivel de complejidad. En la actualidad se emplean programas complejos de simulación que poseen capacidad para una simulación extendida de los diferentes sistemas del vehículo. En [1] se muestran ejemplos de simulación eficiente de trenes de transmisión, desarrollo de sistemas de seguridad activos y análisis en estados cuasi-estáticos, entre otros. Para ello son utilizados diferentes procedimientos, como por ejemplo los gráficos de unión y los modelos multi-cuerpo, entre otros. En las últimas décadas, se ha realizado un esfuerzo especial en investigación, desarrollo e innovación en suspensiones para vehículos, principalmente para vehículos de pasajeros. Estos trabajos incluyen suspensiones pasivas mejoradas y más complejas; las cuales son capaces de brindar un mejor compromiso entre maniobrabilidad y confort durante conducción, garantizando a su vez un diseño del chasis que permite contar con tracción delantera, bajo centro de masa y mejores características aerodinámicas [2].

En la medida que los requerimientos de desempeño impuestas por el mercado y las normas sobre seguridad, maniobrabilidad, confort, entre otras, se hacen más exigentes, la industria automovilística ha encontrado en la simulación dinámica una forma de llevar a cabo pruebas sobre el comportamiento de un vehículo para las diferentes etapas de diseño [3]. Entre los factores externos que afectan el comportamiento dinámico de una suspensión se encuentran el perfil del camino y las maniobras de conducción tales como frenado, aceleración y giros. La suma de estas condiciones tiene como resultado la modificación de la posición del chasis y la geometría de la suspensión originando distribuciones de carga entre las ruedas, que determinan el grado de maniobrabilidad y estabilidad del vehículo.

La maniobrabilidad del vehículo se entiende como la capacidad de este para responder a los comandos de dirección introducidos por el conductor a través del timón y los demás controles, permitiendo dicho cambio de dirección. Se conoce que la respuesta del vehículo a la transferencia de carga, a los cambios de dirección y a las irregularidades del terreno se encuentra directamente relacionada con la suspensión. ''Todo vehículo está conectado al terreno a través de cuatro pequeñas superficies de contacto ubicadas donde las ruedas encuentran el pavimento, a través de estas cuatro superficies de contacto, todas las fuerzas de giro, aceleración y frenado son transmitidas al vehículo. La suspensión de un vehículo está relacionada con la conexión de las ruedas con el vehículo, controlando como el vehículo maniobra y como las cuatro pequeña superficies de contacto son utilizadas'' [4]. Por su parte, la estabilidad está relacionada con cada aspecto operativo del vehículo, desde la tendencia de giro (que puede ser neutra, sobrevirada o subvirada), hasta los aspectos de seguridad como por ejemplo la tendencia al vuelco. ''En general el diseño de una suspensión pasiva es un compromiso con los siguientes aspectos del comportamiento del vehículo: espacio de trabajo de la suspensión, confort en el viaje, llantas, fuerza de contacto con el suelo'' [5].

La ergonomía del vehículo está relacionada con el confort percibido por los ocupantes bajo la influencia de aceleraciones y vibraciones. Las vibraciones son producidas por el funcionamiento del motor, tren de propulsión, maniobras de conducción y por las irregularidades en el terreno; y son percibidas a través del asiento y las interfaces funcionales humano-vehículo. ''La supresión de las vibraciones en una suspensión pasiva depende de la resistencia del resorte, del coeficiente de amortiguamiento y de la masa suspendida. Debido al hecho de que no se pueden satisfacer los requerimientos de confort bajo diferentes condiciones del camino'' [6] es deseable realizar extensas simulaciones en las etapas preliminares de diseño donde las correcciones y cambios son poco costosas. El confort presenta ciertas dificultades para ser evaluado, entre ellas la subjetividad de la comodidad, la gran diversidad de medidas antropométricas, y la necesidad de representar la interacción cuerpo-asiento de manera matemática.

En el presente artículo se describe la dinámica de un vehículo de cuatro ruedas con suspensión independiente del tipo paralelogramos deformables y barras de estabilidad transversal, la cual es una configuración comúnmente utilizada en vehículos deportivos. Las ventajas asociadas con este tipo de suspensión incluyen ''fácil control del centro de balanceo mediante la elección de la geometría de los brazos de control, grandes deformaciones de la suspensión y mayor resistencia al balanceo para una razón de suspensión vertical dada'' [7]. El propósito del presente estudio es desarrollar un modelo que describa la dinámica vertical y de rotación en los planos longitudinal y transversal de un vehículo. Lo anterior para condiciones de conducción que incluyen irregularidades en el terreno, giros y cambios de velocidad. Este modelo resulta apropiado para la determinación de la estabilidad dinámica del vehículo, las cargas a las que se ven sometidos los componentes de la suspensión y el chasis, y el régimen de aceleraciones sobre el ocupante u ocupantes del vehículo con el fin de evaluar parcialmente el grado de confort percibido.

 

Experimental

Modelo básico del vehículo

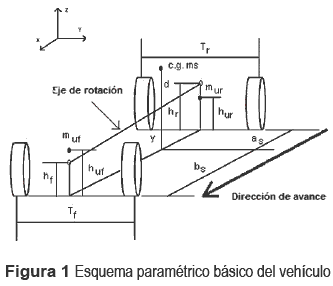
El vehículo considerado consta de cuatro ruedas, con suspensión independiente tipo paralelogramos deformables, barras de estabilización transversal en cada eje, tracción trasera, dirección delantera y con capacidad para un ocupante, situado en el plano longitudinal medio del vehículo. El sistema de referencia del vehículo se encuentra fijo a su centro de gravedad y las posiciones relativas de los puntos de interés son determinadas a partir de este punto. En la figura 1 se muestra el esquema paramétrico básico del vehículo.

 

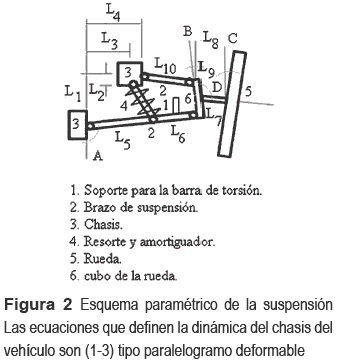
El modelo propuesto posee 7 GdL: desplazamiento a lo largo del eje Z (vertical), rotación alrededor de los ejes X (balanceo) e Y (cabeceo) del chasis, y desplazamiento vertical de las cuatro masas no suspendidas pertenecientes a cada suspensión. Los ejes X, Y y Z pasan por el centro de gravedad del vehículo y el chasis se considera como una estructura rígida. La suspensión de cada rueda posee características geométricas similares. El resorte helicoidal y el amortiguador forman un solo conjunto y sus extremos se encuentran conectados a los mismos puntos de la palanca inferior y del chasis respectivamente [8]. La disposición de las barras, puntos de sujeción, conexión de la barra de estabilidad transversal, resorte, amortiguador y rueda, para la suspensión estudiada se muestra en la figura 2.

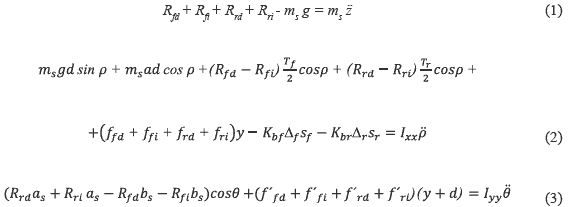
Donde:

R_ij: Fuerza normal actuando en el eje i lado j (N).

z: Posición del c.g. del vehículo (m).

a: Aceleración lateral (ms-2).

g: Aceleración de la gravedad (ms-2).

ρ: Ángulo de balanceo (rad.).

θ: Ángulo de cabeceo (rad.).

b_s: distancia del eje delantero al c.g. (m).

a_s: Distancia del eje trasero al c.g. (m).

I_xx: Inercia alrededor del eje X (kgm²).

I_yy: Inercia alrededor del eje Y (kgm²).

m_s: Masa suspendida (kg).

s_i: Distancia entre apoyos en el chasis de la barra de estabilidad colocada en el eje i (m).

K_bi: Coeficiente de rigidez de la barra de estabilidad transversal del eje i (Nm^-1).

Δ_i: Deformación relativa de los extremos de la barra de estabilidad transversal del eje i (m).

d: Distancia desde el centro de gravedad al eje de rotación (m).

T_f y T_r: Trochas delantera y trasera respectivamente (m).

f_ij y f '_ij: Componentes de fuerzas transversal y longitudinal actuando sobre el chasis en el eje i lado j respectivamente (N).

y: Distancia vertical desde el suelo al eje de rotación para la posición del centro de gravedad (m).

d: Distancia vertical desde el centro de gravedad al eje de rotación (m).

Siendo los subíndices, i: f (eje delantero) o r (eje trasero) y j: d (lado derecho) o i (lado izquierdo).

En (2) los dos primeros términos reflejan la contribución al momento de balanceo de la masa suspendida al salir de su posición de equilibrio debido a la aceleración lateral; los siguientes dos términos tienen en cuenta el momento de las reacciones normales que ejerce cada suspensión sobre el chasis del vehículo; el cuarto término toma en cuenta la contribución al momento de las fuerzas transversales que ejerce cada suspensión sobre el chasis del vehículo; y los últimos dos términos son los momentos de estabilización de las barras transversales delantera y trasera respectivamente.

 

Modelo dinámico para una suspensión aislada (1/4 de vehículo)

El propósito de este primer modelo de ¼ de vehículo es determinar la posición del chasis referida a tierra para cualquier instante de tiempo. El modelo equivalente utilizado consiste en la unión de dos sistemas dinámicos, masa suspendida-resorte-amortiguador y masa no suspendida-resorte- amortiguador, ambos conectados en serie. La señal de entrada o excitación al sistema de suspensión corresponde a la altura del pavimento con respecto a un nivel de referencia.

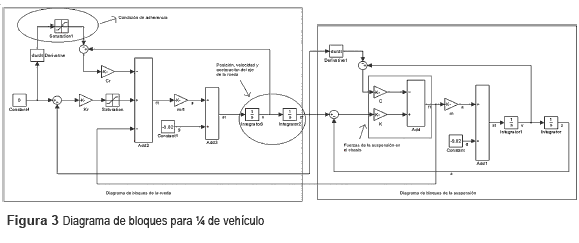
El conjunto de expresiones que describen el funcionamiento de una suspensión aislada se implementa utilizando la interfaz gráfica de Simulink^®Matlab^®, y en la figura 3 se muestra el diagrama de bloques correspondiente. En el primer bloque de suma se representa el eje de la rueda y sobre este se realiza la suma de las fuerzas que intervienen. El segundo bloque rectangular de suma tiene en cuenta el peso de la masa no suspendida; con este último bloque se obtiene la aceleración absoluta del eje de la rueda; la velocidad relativa con la cual se calcula la fuerza de amortiguación; y la diferencia de posición con la cual se calculan las fuerzas elásticas generadas por el resorte y la rueda. Las cuatro ecuaciones diferenciales, una por cada suspensión independiente, tienen una estructura como la mostrada en (4).

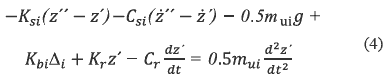
Donde:

m_ui: Masa no suspendida en el eje i (kg).

K_r: Coeficiente de rigidez de la rueda (Nm^-1).

C_r: Coeficiente de amortiguación de la rueda (Nsm^-1).

K_si: Coeficiente de rigidez de la suspensión en el eje i (Nm^-1).

C_si: Coeficiente de amortiguación en el eje i (Nsm^-1).

z': Posición relativa del eje de la rueda respecto a la vía (m).

z'': Posición relativa del punto de conexión del sistema resorte-amortiguador al chasis (m).

Finalmente, para acoplar todo el modelo se debe incluir la interacción entre las masas suspendida y no suspendida respectivamente.

 

Modelo dinámico para toda la suspensión del vehículo

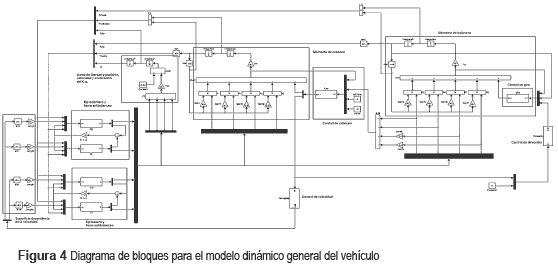
Realizando la generalización del modelo de ¼ de vehículo a los planos longitudinal y transversal respectivamente se obtiene el modelo general del vehículo. Este contiene los siete grados de libertad descritos, e incluye también los módulos de dirección y de giro del vehículo, la acción de las barras estabilizadoras y las condiciones de aceleración en los planos longitudinales y transversales del vehículo. El diagrama de bloques para el modelo dinámico general del vehículo se muestra en la figura 4, donde se aprecia que para cada eje se ha generado un subsistema que representa la operación de la barra estabilizadora, donde se calcula la diferencia de altura entre los extremos de esta, para calcular el valor de las fuerzas de estabilización aplicadas sobre cada suspensión. También, se anota que las funciones de entrada que representan el perfil de la vía fueron agrupadas en un subsistema.

 

Condiciones empleadas en las simulaciones

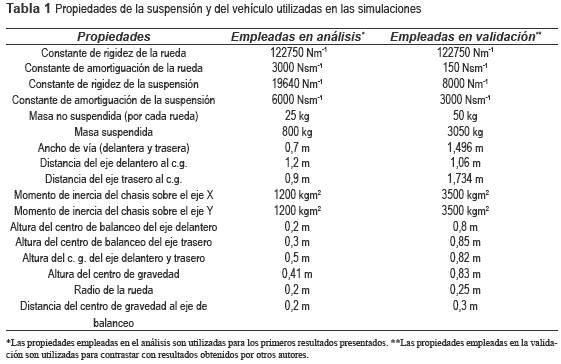
Los módulos de entrada al modelo dinámico general desarrollado en este trabajo permiten considerar variados escenarios de maniobras de conducción; incluidas maniobras compuestas como por ejemplo, frenada en un giro o aceleración/frenada con excitación de la vía. Lamentablemente, la literatura especializada en el tema de dinámica vehicular se limita a presentar resultados de simulación para maniobras de conducción simples y aisladas; lo cual es un inconveniente para validar, por vía de comparación de resultados, maniobras complejas como las que son simuladas en el presente trabajo. Por lo anterior, en este trabajo se simulan tanto maniobras simples como combinaciones de maniobras. Las maniobras simples son empleadas para validar el modelo desarrollado con resultados de otros autores. En el tabla 1 aparecen las propiedades físicas de la suspensión y del vehículo en general empleadas en las simulaciones.

 

Las condiciones de simulación empleadas son: (a) Vía plana; (b) Vía con perfil sinusoidal con longitud de onda de 12 m y dos variantes. Primera variante, ruedas izquierdas y derechas sobre camino sinusoidal de amplitud 0,04 m; y segunda variante ruedas del lado derecho sobre camino sinusoidal de amplitud 0,04 m y ruedas del lado izquierdo sobre camino sinusoidal de amplitud 0,02 m (en fase); (c) Movimiento a velocidad constante (v=12,5 ms^-1); (d) Acción de acelerar: Parte de velocidad inicial nula hasta que se alcanza una velocidad final de 12,5 m/s (a=3,93 ms^-2); (e) Acción de frenado: velocidad inicial de 12,5 ms^-1 hasta una velocidad final nula (a=-3,93 m/s^-2). La desaceleración comienza 1 s después de iniciada la simulación: (f) Maniobra de giro seguida de contragiro: velocidad de 4 ms^-1, radio de giro variable con patrón sinusoidal y radio de giro mínimo igual a 8,48 m; (g) Maniobra de giro con radio de giro constante igual a 8,48 m, con velocidad inicial de 4 ms^-1 y velocidad final nula (a=-3,92 ms^-2); y por último (h) Maniobra de contragiro con radio de giro constante igual a 8,48 m, con velocidad constante de 4 ms^-1 sobre vía con perfil sinusoidal (segunda variante).

 

Resultados y discusión

Resultados para la cinemática general del vehículo

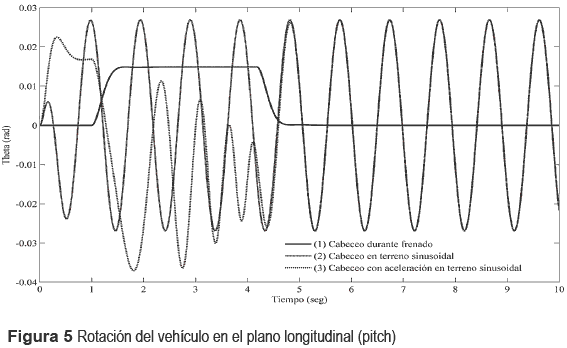
En la figura 5 aparecen los resultados del análisis para el plano longitudinal del vehículo. La curva (1) muestra el comportamiento del ángulo de cabeceo del vehículo para una condición de frenado (a=-3,92 ms^-2). El vehículo se inclina hacia adelante (zambulle) un ángulo de cabeceo de 0,86° durante un tiempo de 2,65 s. Esta pequeña inclinación de cabeceo se percibe favorablemente por los ocupantes del vehículo, por lo que está suspensión presenta una respuesta adecuada en este aspecto. La curva (2) muestra el comportamiento para velocidad de desplazamiento constante (v=12,5 ms^-1) y una excitación sinusoidal sobre las ruedas igual a la planteada para el caso de análisis anterior. Para esta nueva situación se aprecia que luego de un pequeño efecto transitorio de apenas una onda la respuesta del vehículo se vuelve estable, ocurriendo una oscilación uniforme en el plano longitudinal del vehículo con un ángulo límite de zambullida/levantamiento igual a ±1,57°. También, es necesario hacer notar que las curvas (2) y (3) convergen luego de T≥5 s a una condición uniforme de balanceo en el plano longitudinal del vehículo. Por último, la curva (3) muestra el resultado para una condición de aceleración, partiendo de velocidad nula, con una excitación sinusoidal sobre las ruedas (A=0,04 m). Se observa aquí la superposición de dos efectos; primero ocurre el levantamiento de la parte frontal del vehículo producto al arranque, luego ocurre el balanceo sinusoidal del vehículo en su plano longitudinal producto a la excitación proveniente de la vía. Es interesante el hecho que las separaciones entre ondas no solo se van acortando producto a la mayor velocidad que va alcanzando el vehículo, sino también que su amplitud se va haciendo menor producto al efecto disipador combinado de los amortiguadores de las suspensiones delanteras y traseras respectivamente. El ángulo límite de cabeceo positivo es igual a 1,31°, mientras que el ángulo límite de cabeceo negativo resultó igual a -2,17°.

 

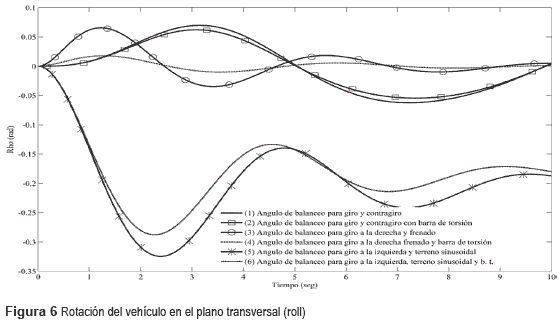
En la figura 6 aparecen los resultados del análisis para el plano transversal del vehículo. Se analizan tres tipos de situaciones de conducción: giro y contragiro; giro con frenada; y contragiro con excitación sinusoidal de la vía. Para estudiar la influencia que tienen las barras de estabilización transversal en la estabilidad transversal del vehículo, las tres situaciones anteriores se analizan con y sin estos dispositivos instalados. La curva (1) muestra el resultado para la maniobra de giro y contragiro del vehículo sin barras de estabilidad transversal. La fase de giro y contragiro no son iguales dado que la acción de giro perturba a la acción posterior de contragiro; a pesar de ello los valores límites del ángulo de inclinación transversal son parecidos para ambas fases de la maniobra (ρ_giro =12,6° y (ρ_contragiro =-12,5°). Al activarse las barras de estabilización transversal (curva 2) ocurre una disminución del ángulo límite de inclinación transversal del 12%. Si se quiere disminuir aún más el ángulo de inclinación transversal se podría incrementar la rigidez de las barras transversales, aunque esto en exceso conlleva al detrimento de la percepción de confort durante conducción del vehículo. La curva (3) muestra el resultado de la maniobra de giro y frenado simultáneo del vehículo sin barras de estabilidad transversal. El ángulo de inclinación transversal máximo resultó igual a 4,2°. La curva (4) muestra el resultado cuando se emplean las barras de estabilidad transversal. Con el uso de estos dispositivos se logra un efecto relativamente débil para esta clase de maniobra, disminuyendo el ángulo de inclinación transversal solo en un 8%. Es necesario hacer notar que el ángulo de inclinación transversal en esta maniobra es pequeño debido a que el tiempo de sostenimiento de la aceleración lateral es corto, y además este último disminuye rápidamente debido a la desaceleración de frenado. No obstante, es interesante el pequeño balanceo transversal del vehículo que se aprecia, el cual es disipado por los amortiguadores, incluso luego que el vehículo se ha detenido por completo. Por último, la curva (5) muestra el efecto de un contragiro con excitación sinusoidal de la vía (A=0,04 m) a velocidad de desplazamiento constante (v=12,5 ms^-1) sobre el ángulo de inclinación transversal, para el vehículo sin barras de estabilidad transversal. Esta condición resultó ser la más crítica para el vehículo, provocando un ángulo de inclinación transversal máximo igual a 18,4°. Con el uso de barras de estabilidad transversal se logra disminuir el ángulo de inclinación transversal máximo a un valor de 16,3° (curva 6), luego los valores picos de inclinación inducidos por las irregularidades del camino se mantienen en 11,6°. Como conclusión parcial de este trabajo se puede resaltar el hecho de lo versátil y flexible que resulta el modelo dinámico de suspensión del vehículo para describir distintas condiciones de maniobras; brindando soluciones para el ángulo de cabeceo (pitch) y de inclinación transversal (roll) del vehículo en función del tiempo, lo cual puede ser empleado para caracterizar el desempeño de una suspensión del tipo analizada. Las maniobras más peligrosas resultaron ser la de giro en una vía con irregularidades, seguida por la de realizar un giro y contragiro, ambas a velocidad de desplazamiento constante. Se evidencia la mejoría en la dinámica transversal del vehículo cuando se utilizan las barras de estabilidad transversal.

 

Comportamiento de las fuerzas sobre la suspensión

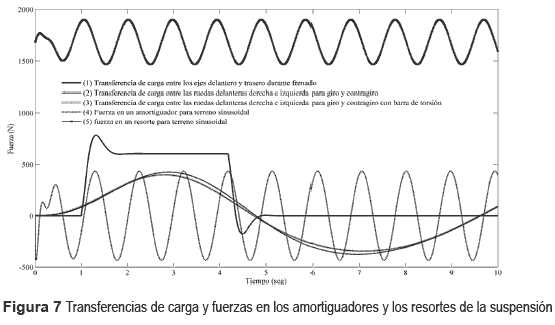
En la figura 7 aparece el comportamiento de las fuerzas sobre la suspensión del vehículo bajo distintas maniobras. La curva (1) representa la transferencia de carga entre el eje delantero y el trasero, para la condición de frenado (a=-3,93 ms^-2). En el comienzo y la finalización de la acción de frenado se observa el efecto de amortiguación de la suspensión. Durante el frenado ocurre una transferencia de carga igual a 600 N de las ruedas traseras hacia las delanteras. Las curvas (2) y (3) muestran la transferencia de carga que ocurre desde las ruedas de un lado hacia las del lado opuesto, para una suspensión sin y con barras de estabilidad transversal respectivamente, cuando el vehículo realiza la maniobra de giro y contragiro. En la primera fase (giro) de la maniobra, ocurre la mayor transferencia de carga desde las ruedas del lado derecho hacia las de la izquierda, con valor igual a 3330 N; luego en la segunda fase (contragiro) de la maniobra la transferencia de carga es igual a -2850 N. Lo anterior para la suspensión sin barras de estabilización instaladas. En caso de tener el vehículo las barras de estabilización activas, los valores de transferencia de carga anteriores se reducen en 5,0% y 8,6% respectivamente. Además, mediante el modelo se aprecia que en caso de emplear radios de giros menores, o mayor velocidad de desplazamiento, el modelo es capaz de predecir la pérdida de estabilidad transversal (vuelco) del vehículo o su derrape por pérdida de adherencia. Por último, las curvas (4) y (5) muestran el comportamiento de las fuerzas en los amortiguadores y los resortes de la suspensión respectivamente, para una conducción sobre una vía con excitación sinusoidal (A=0,04 m) a velocidad de desplazamiento constante.

 

Aceleraciones para la posición del conductor

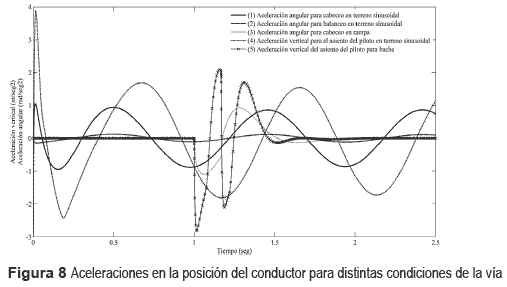
En la figura 8 aparece el comportamiento de las aceleraciones mencionadas para distintas situaciones de excitación de la vía (escalón, rampa y terreno sinusoidal). Las curvas (1) y (3) muestran la aceleración angular en el plano longitudinal para una vía con perfil sinusoidal y rampa respectivamente. La curva (2) muestra el comportamiento del ángulo de inclinación transversal cuando las ruedas de un solo lado del vehículo sufren una excitación sinusoidal. La curva (4) muestra la aceleración vertical para la posición del conductor del vehículo inducido por un camino de perfil sinusoidal de amplitud diferente al lado izquierdo y derecho de la trocha del vehículo respectivamente. Por último, la curva (5) muestra la aceleración vertical generada por una depresión de profundidad igual a 0,04 m. De particular interés por los mayores valores resulta la aceleración vertical, que fluctúa entre (-2,5 ms^-2/+2,0 ms^-2), y la aceleración angular en el plano longitudinal, que alcanza un valor máximo de 0,98 rads^-2, provocadas ambas por una depresión en la vía.

 

Comparación con resultados externos y validación del modelo

En este trabajo se realiza una comparación con los resultados obtenidos por otros autores como método de validación del modelo desarrollado. De la extensa revisión realizada sobre artículos que trabajan en modelos de dinámica vehicular, el de Attia, y el de Cronje' y Els respectivamente [9, 10], muestran resultados de respuesta dinámica orientados a una suspensión de paralelogramos deformables con barra de estabilidad transversal. Lo anterior convierte en idóneos a estos trabajos para fines de comparación de resultados.

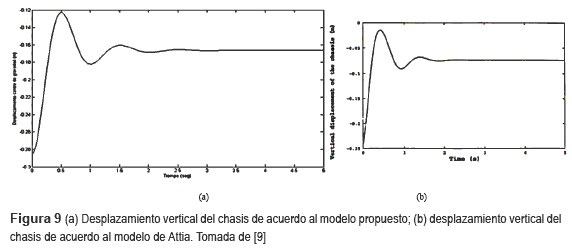
La figura 9 muestra los resultados obtenidos con el modelo propuesto (a), y con el modelo presentado por Attia [9] (b), cuando se somete el chasis a la acción de una fuerza vertical que lo obliga a moverse fuera de su posición de equilibrio. En ambos casos el vehículo entra en oscilaciones amortiguadas hasta alcanzar luego de cierto tiempo la posición de equilibrio. Attia plantea para esta simulación que ''la comparación con el programa DAP-3D muestra una completa concordancia con los resultados de la simulación''.

 

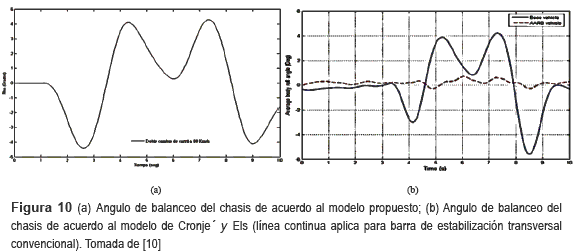
Por su parte, Cronje' y Els en su estudio [10] simulan un doble cambio de carril para un vehículo modelo Land Rover 110. En este caso los parámetros de la simulación se definen con los valores propios de esta clase de vehículo. La figura 10(a) muestra los resultados obtenidos con el modelo propuesto en este trabajo, y en la (b) los resultados obtenidos en el otro trabajo mencionado, para el ángulo de balanceo del vehículo cuando se realiza la maniobra de cambio de carril.

Al comparar los resultados obtenidos en el presente trabajo con sus contrapartes, se aprecia que los resultados dinámicos en ambos casos siguen la misma clase de comportamiento. Adicionalmente, es importante resaltar como aporte del presente artículo la manera exhaustiva con que se logra mostrar el comportamiento dinámico del vehículo para la categoría de suspensión estudiada; no encontrándose en la revisión realizada otros trabajos que muestren resultados tan completos en cuanto a combinaciones de maniobras de conducción y condiciones del perfil de la vía.

 

Conclusiones

El modelo presentado en este trabajo es capaz de describir el comportamiento dinámico de un vehículo de cuatro ruedas con suspensión independiente manteniendo una gran simplicidad y versatilidad, siendo posible cambiar fácilmente los parámetros de entrada (dimensiones, rigidez, amortiguación, etc.) y también añadir características adicionales al modelo. Son obtenidos los resultados sobre la dinámica longitudinal y transversal del vehículo bajo la acción de varias maniobras de conducción, entre estos se encuentran algunas respuestas verificables mediante la experiencia, como el cabeceo durante el frenado o el balanceo hacia el exterior de la curva durante un giro. Esta información permite determinar la posición, velocidad y aceleración de cualquier punto en el vehículo. También es posible obtener información relativa a las fuerzas que actúan en el sistema de suspensión y la transferencia de carga entre las ruedas para distintas maniobras de conducción.

El modelo desarrollado es capaz de predecir la estabilidad transversal de un vehículo. Por ejemplo, cuando se simula un giro en condiciones desfavorables (radio de giro muy pequeño y/o velocidad muy alta) el ángulo de inclinación transversal alcanza valores tan altos que indica un vuelco, o la transferencia de carga es tan significativa que provoca la pérdida de adherencia de las ruedas ubicadas del lado interno de la curva. Por otro lado, el confort puede evaluarse parcialmente a partir de las aceleraciones lineales y angulares para la posición del conductor.

El modelo desarrollado es verificado por medio de la comparación con los resultados obtenidos por otros autores. Se encuentra muy buena correspondencia tanto en tendencias y comportamientos de la dinámica general del vehículo, como en las magnitudes de las variables de respuesta que definen la dinámica vehicular (para iguales parámetros de entrada al modelo).

 

Referencias

1. J. Andreasson. The Vehicle Dynamics Library: New Concepts and New Fields of Application. Presented in 8^th Modelica Conference. Dresden, Germany. 2011. pp. 20-22.         [ Links ]

2. D. Cao, X. Son, M. Ahmadian. ''Editors' perspectives: road vehicle suspension design, dynamics, and control''. Vehicle System Dynamics. Vol. 49. 2011. pp. 3-28.         [ Links ]

3. C. Kim, A. Mijar, J. Arora. ''Development of Simplified Models for Design and Optimization of Automotive Structures for Crashworthiness''. Structural and multidisciplinary optimization. Vol. 22. 2001. pp. 307-321.         [ Links ]

4. R. Berman. Dynamic Modeling and Analysis of the Suspension System of the Bailey Edwards LMP II Prototype. University of the Witwatersrand. Johannesburg, South Africa. 2010. pp. 4.         [ Links ]

5. E. Bello, I. Ogedengbe, A. Osasona, A. Akinola. ''Compromises in Vehicle Suspension Design''.Journal of Mechanics Engineering and Automation. Vol. 2. 2012. pp. 441-445.         [ Links ]

6. S. Abramov, S. Mannan, O. Durieux. ''Semi-Active Suspension System Simulation Using SIMULINK''. International Journal of Engineering Systems Modeling and Simulation. Vol. 1. 2009. pp. 101-114.         [ Links ]

7. D. Güler. Dynamic Analysis of a double Wishbone Suspension. Tesis de Maestría. Izmir Institute of Technology. Izmir, Turkey. 2006. pp. 1-26.         [ Links ]

8. B. Hall. ''Suspension systems and components''. An introduction to Modern Vehicle Design. J. Happian (editor). First Edition. Ed. Butterworth Heinemann. Linacre House, Jordan Hill. Oxford, England. 2002. pp. 277-326.         [ Links ]

9. H. Attia. ''Dynamic modeling of the double wishbone motor-vehicle suspension system''. European Journal of Mechanics A/Solids. Vol. 21. 2002. pp. 167-174.         [ Links ]

10. P. Cronje', P. Els. ''Improving off-road vehicle handling using an active anti-roll bar''. Journal of Terramechanics. Vol. 47. 2010. pp. 179-189.         [ Links ]