Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.69 Medellín Oct./Dec. 2013
ARTÍCULO ORIGINAL
Modelado del proceso de maquinado mediante el MEF y el uso de metamodelos con lógica difusa y regresión lineal
Machining process modeling by means of FEM and the use of metamodels with fuzzy logic and linear regression
Edgar Andrés Patiño-Nariño, José Manuel Arroyo-Osorio*, Diego Alexander Garzón-Alvarado, Carlos Julio Cortés-Rodríguez
Departamento de Ingeniería Mecánica y Mecatrónica. Universidad Nacional de Colombia, Cra. 30 No. 45-03. C.P. 111321. Bogotá, Colombia.
*Autor de correspondencia: teléfono: + 57 + 1 + 316 5582, fax: + 57 + 1 + 316 5586, correo electrónico: jmarroyoo@unal.edu.co (J. Arroyo)
(Recibido el 12 de abril de 2011. Aceptado el 19 de septiembre de 2013)
Resumen
Se implementó un modelo que simula el proceso de maquinado ortogonal de metales por el método de elementos finitos (MEF). Para el desarrollo del modelo se utilizó el programa Ansys Flotran. El material de trabajo se simuló como un fluido de alta viscosidad que impacta un sólido cuya geometría es la de la arista de corte. A partir del modelo numérico, se realizó un diseño de experimentos factorial fraccionado usando el programa Minitab, donde las variables de entrada seleccionadas fueron: profundidad de corte, velocidad de corte, ángulo de desprendimiento, densidad y viscosidad del fluido. Las variables de salida consideradas fueron la velocidad de salida de la de viruta y la posición del punto de estancamiento en la formación de la viruta. Se realizaron dos metamodelos funcionales que representan la interacción entre las variables de entrada y de salida del modelo MEF. El primer metalmodelo se realizó por medio de una regresión lineal y el segundo por lógica difusa. Los experimentos con los dos metamodelos mostraron que dos de las variables de entrada (profundidad de corte y ángulo de desprendimiento), tienen la mayor influencia en las variables de salida elegidas: velocidad de la viruta y en la posición del punto de estancamiento. El metamodelo basado en lógica difusa presentó una mejor representación de la relación entre las variables de entrada y de salida.
Palabras clave: Diseño factorial de experimentos, maquinado, lógica difusa, metamodelos, método de elementos finitos
Abstract
In this work it was implemented a numerical model that simulates the process of orthogonal machining of metallic materials by means of the Finite Elements Method (FEM). For the development of the model, the program Ansys Flotran was used. The material was simulated as a high viscosity fluid crashing against a solid with the cutting edge geometry. From the numerical model it was made a factorial fractionated design of experiments using Minitab software, where the selected input variables were: cutting speed, depth of cut, rake angle, density and viscosity of the fluid. The considered output variables were the velocity of chip and the position of the stagnation point. Two functional metamodels of the FEM model were made, the first one by determining the empirical equations by means of a linear regression. The second was made by establishing functions based on fuzzy logic. The experiments with both metamodels showed that the depth of cut and the rake angle have the greater influence in the chip speed and in the position of the stagnation point. The metamodel based on fuzzy logic presented a better representation between the input and output variables.
Keywords: Factorial design of experiments, fuzzy logic, finite elements method, machining, metamodels
Introducción
El proceso de maquinado es uno de los métodos de fabricación más utilizados en la industria gracias a su amplia aplicación en metales y aleaciones [1, 2]. Para llevar a cabo una adecuada planeación de los procesos de maquinado es fundamental el conocimiento de la compleja relación entre una gran cantidad de variables. Obtener información experimental de los procesos de maquinado es costoso y complejo en términos de tiempo, material y procedimientos [3, 4]. Por esta razón es muy importante el desarrollo de modelos matemáticos precisos para el análisis del proceso [5] y para optimizar las condiciones de operación [6].
El desarrollo de modelos matemáticos para la descripción de los aspectos más relevantes del maquinado comenzó con relaciones empíricas, como la conocida ecuación de vida de la herramienta de Taylor, desarrollada a finales del siglo XIX [6]. En los trabajos de Ernst y Merchant [7, 8], se establecieron los fundamentos del análisis de la mecánica de los procesos de maquinado, los cuales han sido vigentes por más de seis décadas [9]. Adicionalmente, debido a la necesidad de aumentar la precisión de los procesos de maquinado y establecer una mejor correlación entre las variables involucradas se han hecho importantes avances en diseño de experimentos y regresiones estadísticas [10], análisis numérico utilizando el método de elementos finitos (MEF) [11], modelos empíricos y basados en técnicas de computación flexible como lógica difusa [12, 13].
Entre los procesos numéricos utilizados para simulación del maquinado, el método de elementos finitos (Finite Element Modeling) es el más frecuente [14-16]. El primer antecedente conocido es del año 1971 por Zienkiewicz y Kakino [17], quienes presentaron un modelo de flujo de material en forma de viruta predefinida. Posteriormente Shirakashi y Usui [18] desarrollaron un modelo que realiza cambios en la forma de la viruta. Para ello utilizaron modelos en el tiempo y un modelo de la fricción entre la viruta y la herramienta. Además en este mismo trabajo se involucra la distribución de temperatura y la variación de los esfuerzos en función de la deformación. Entre las técnicas de los elementos finitos para el proceso de formación de viruta se han empleado enfoques tales como Lagrangiano, Euleriano y formulaciones mixtas como la ALE (arbitrary Lagrangian-Eurelian) [19]. Una falencia de estas investigaciones es que se han preocupado más del desarrollo del método que por su aplicación inmediata [20]. Recientemente el desarrollo de MEF para el análisis del corte de metales, ha tenido un importante auge debido a los avances en capacidad de cómputo y a la disponibilidad de códigos comerciales [21].
En éste trabajo se desarrolló un modelo simplificado del maquinado ortogonal en 2D utilizando el paquete comercial Ansys FLOTRAN, simulando la formación de la viruta mediante dinámica computational de fluidos. El estudio se enfocó en la región de cizallamiento primaria, de gran importancia en el estudio científico del maquinado [22, 23].
El modelo MEF se utilizó para realizar un plan de experimentos en un diseño factorial fraccionado de 2(5-1) para cinco variables de entrada en dos niveles [24], el cual fue implementado en el programa MINITAB. Las cinco variables de entrada consideradas fueron: profundidad de corte, velocidad de corte, ángulo de desprendimiento de la arista de corte y la densidad y viscosidad del material de trabajo. Las variables de salida seleccionadas fueron la velocidad de la viruta y la posición del punto de estancamiento. Las investigaciones en maquinado han mostrado que la velocidad de la viruta sobre la superficie de salida de la herramienta está relacionada con el fenómeno de formación de la viruta, que involucra variables como flujo de esfuerzos y velocidad de deformación [25, 26]. La posición del punto de estancamiento influye en el espesor de viruta sin cortar y en la profundidad mínima de corte. Estas dos variables son fundamentales en maquinado de precisión y en micro y nano maquinado [27, 28]. Finalmente se desarrollaron dos metamodelos (un modelo del modelo) [29, 30] con el propósito de determinar cuáles variables de entrada presentaban mayor efecto en las variables de salida. El primer metamodelo se realizó por medio de regresión estadística con el programa MINITAB [31], y el segundo empleando la técnica de lógica difusa [12] usando el FUZZY LOGIC TOOLBOX de MATLAB [32].
Modelo matemático
En este trabajo se propone la representación del material de trabajo como un fluido de elevada viscosidad con el objetivo de representar la alta velocidad de deformación característica del proceso de maquinado. Se utilizó un modelo Navier-Stokes [33] (en 2D) para representar el fluido, suponiendo incompresibilidad. Definiendo condiciones de frontera, el modelo de se representa con las ecuaciones 1a, 1b y 1c en donde: Vx, Vy representan componentes de la velocidad; ρ es la densidad, P es la presión y μ la viscosidad. Las fuerzas del diferencial de fluido en unidad de masa se toman en las componentes X e Y cómo y D representa la derivada material.
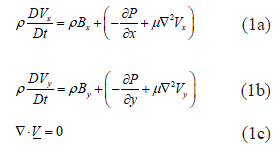
Modelo computacional
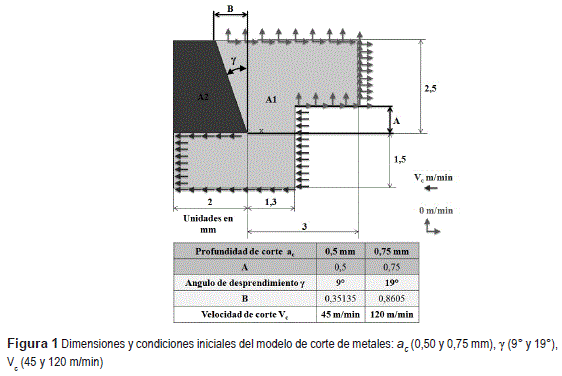
En la figura 1 se ilustra el esquema de maquinado ortogonal desarrollado en Ansys, mostrando el material de trabajo (área A1) y la herramienta de corte (área A2). La herramienta de corte se simula como un material sólido, con densidad de 7000 kg/m3 (valor aproximado de la densidad de una herramienta de corte tipo CERMET [34]). El material de trabajo se representó como un fluido y la velocidad de corte (Vc) se representó como la velocidad de flujo del fluido, la profundidad de corte (ac) se representa por la dimensión A y el ángulo de desprendimiento (γ) por la dimensión B en la figura 1. A las líneas de contorno del área A1 se asignó una velocidad inicial nula (ver figura 1), para asemejar el comportamiento de equilibrio [35]. A la frontera que representa la superficie de salida de la herramienta no se asigna valor inicial, al suponer que la interacción herramienta - material de trabajo se mantiene en equilibrio durante la formación de la viruta [5] (ver figura 1).
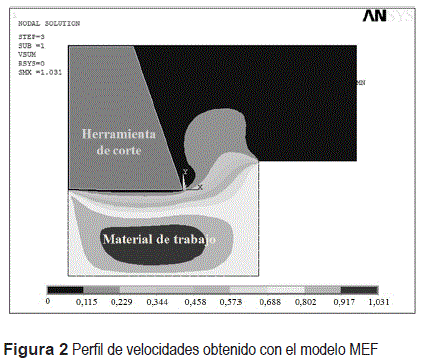
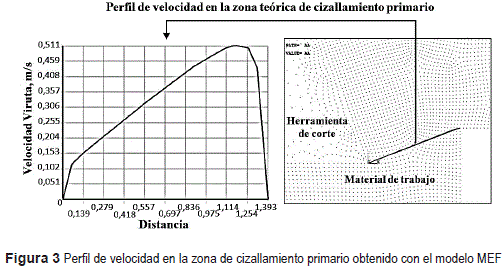
En la figura 2 se muestra el perfil de velocidades y en la figura 3 se observa el perfil de velocidades en la zona de cizallamiento primario obtenidos con la simulación para el caso de γ = 9°, ac = 0,5 mm, Vc = 45 m/min, densidad y viscosidad del material de trabajo 2700 kg/m3 y 106 N*s/m2 respectivamente.
Diseño de experimentos
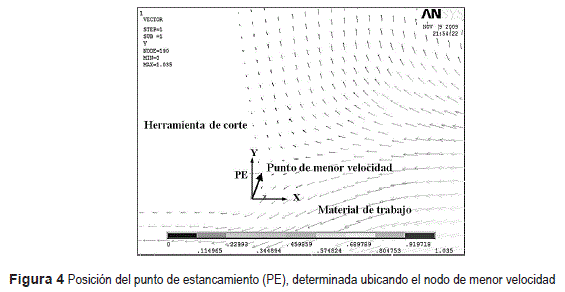
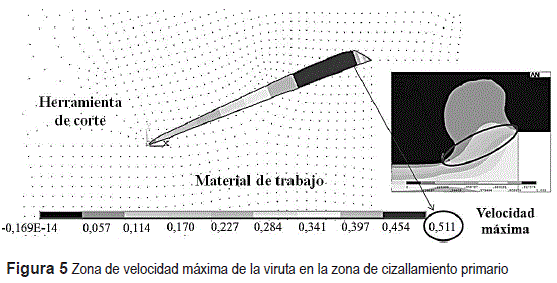
Para el diseño de los experimentos con el modelo desarrollado, se utilizo el programa MINITAB. Las salidas consideradas fueron la posición del punto de estancamiento (PE) y la velocidad de salida de la viruta (Vchip). La posición del punto de estancamiento (PE) se determina ubicando sobre la superficie de desprendimiento el punto con velocidad cero (ver figura 4). La posición espacial de PE con respecto a la componente Y del sistema de referencia se ubica en la punta de la herramienta de corte (ver figura 4). La velocidad de la viruta se considera máxima en la zona de cizallamiento primario (ver figura 5).
Modelo factorial fraccionado 2(5-1)
Se consideró un diseño de cinco variables de entrada en dos niveles para identificar las variables de entrada con mayor efecto en las variables de salida [36]. Los valores de los dos niveles de las variables de entrada consideradas se seleccionaron de la literatura [14, 25, 26] y fueron: ángulo de desprendimiento (γ) 9° y 19°, profundidad de corte (ac) 0,5 y 0,75 mm, velocidad de corte (Vc) 45 y 120 m/min, densidad materiales de trabajo: acero 7850 kg/ m3 y aluminio 2700 kg/m3 [37] y viscosidad materiales de trabajo: acero 106 y aluminio 107 N*s/m2.
De esta forma se tiene un modelo factorial 25, con 32 corridas o experimentos. Para disminuir el número de experimentos se utiliza un modelo fraccionado de menor resolución. El fraccionamiento se realiza disminuyendo estos a la mitad, obteniendo un modelo 2(5-1), de resolución V (cinco) el cual permite identificar los efectos independientes principales de la interacción entre las variables [24].
Discusión de resultados, modelo factorial fraccionado 2(5-1)
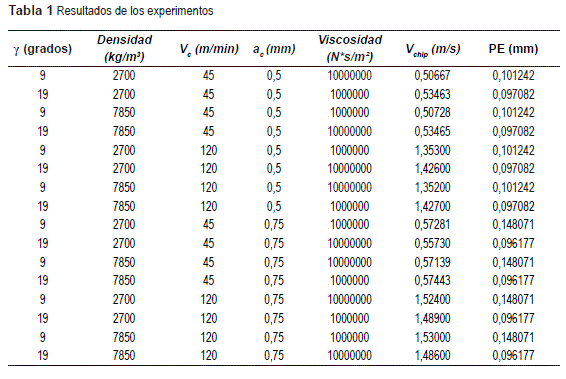
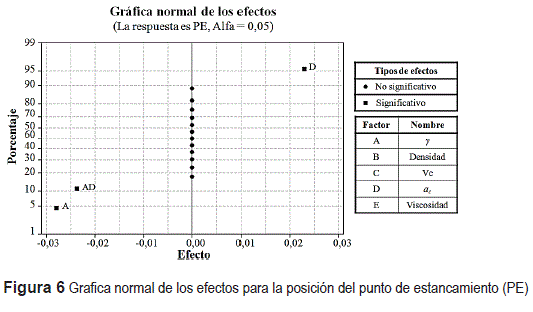
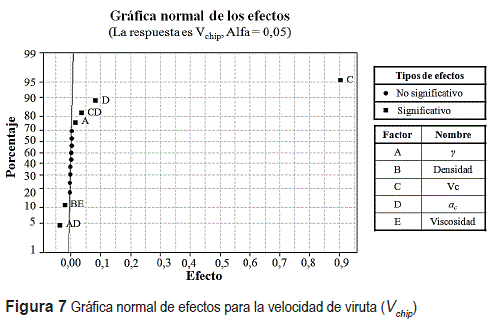
Utilizando MINITAB se definieron los experimentos que se procesaron con el modelo de maquinado en Ansys. Los resultados se muestran en la tabla 1, se utilizó un diseño de experimentos factorial fraccionado 25-1 con variables de entrada: profundidad de corte (ac), ángulo de desprendimiento (γ), Velocidad de corte (Vc), viscosidad del material de trabajo (Viscosidad), densidad del material de trabajo (Densidad) y variables de salida: velocidad de viruta (Vchip) y posición del punto de estancamiento (PE). Para el análisis se empleó la herramienta interacción de efectos [36] en las variables salida con respecto a las variables de entrada. Los resultados se ilustran en las figuras 6 y 7 de los efectos normales para PE y Vchip, los puntos que se encuentran más alejados tanto a la derecha como a la izquierda de la línea recta en 0,00 indican que estadísticamente tienen un efecto más significativo en la variable de salida estudiada.
La figura 6 es la gráfica normal de los efectos para la posición del punto de estancamiento (PE), donde ''Porcentaje'' es la normalización de menor a mayor de los valores de los efectos en las variables de salida, ac es la profundidad de corte, γ representa el ángulo de desprendimiento, Vc es la velocidad de corte, ''Viscosidad'' se refiere a la viscosidad del material de trabajo y ''Densidad'' es la densidad del material de trabajo. De acuerdo con los resultados de los experimentos con el modelo MEF la posición del punto de estancamiento solo dependería de las variables geométricas, ac y γ, como se observa en la figura 6. Lo anterior no es consecuente con la realidad física mostrando una limitante en el modelo MEF planteado, pues se sabe por evidencia experimental que las propiedades del material de trabajo así como la velocidad de corte tienen una influencia importante en la posición del punto de estancamiento [38, 39].
Según los resultados de los experimentos con el modelo MEF, la velocidad de la viruta Vchip depende de las tres variables Vc, γ y ac , como se observa en la figura 7, este resultado es consistente con experimentos físicos del proceso de maquinado [3, 23]. Adicionalmente se encontró que la densidad y la viscosidad del material de trabajo influyen también en la V chip, situación interesante que no se encuentra en la teoría clásica del proceso de maquinado [6, 40] pero que ocurre según verificación experimental [3].
Metamodelo utilizando lógica difusa
Usando lógica difusa con la herramienta FUZZY LOGIC TOOLBOX de MATLAB [32], se implementó un metamodelo [29] basado en los experimentos con el modelo MEF. El modelado por lógica difusa es una herramienta no probabilística, en la que se parametrizan valores verdaderos de problemas de los cuales no se tiene un conocimiento preciso y con altos niveles de incertidumbre [41]. La lógica difusa ya ha sido empleada para análisis y optimización en procesos de maquinado [42-44] debido a su amplia funcionalidad en la representación de datos con alta variabilidad.
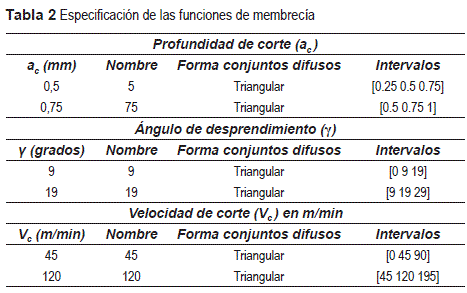
Para la formulación del modelo difuso se emplearon funciones de membrecía compuestas por conjuntos difusos de forma triangular, que se definen con intervalos de tres valores (ver tabla 2), dos valores extremos con el mínimo grado de pertenecía (igual a cero) y el valor intermedio con el máximo grado de pertenecía (igual a uno) [13]. Se uso el condicional AND para todas las reglas, la implicación MIN para el grado de pertenecía en los conjuntos difusos, la agregación MAX en las funciones de membrecía y la defusificación mediante el método del centroide [13, 43]. El metamodelo está compuesto por tres entradas cada una con dos conjuntos difusos, doce reglas de las cuales cuatro están relacionadas con la salida PE y ocho relacionadas con Vchip. Las salidas son PE con tres conjuntos difusos y Vchip con siete.
Entradas difusas
De acuerdo con el análisis factorial se tomaron como variables de entrada aquellas que presentaron efectos significativos en el modelo (ver figuras 6 y 7). De esta manera, las entradas consideradas fueron la profundidad de corte (ac), ángulo de desprendimiento (γ) y Velocidad de corte (Vc). Como se puede observar en la tabla 2, para cada entrada se definieron dos conjuntos difusos que fueron nombrados según los valores usados en el diseño de experimentos, estos valores tienen el máximo grado de pertenencia en los intervalos de los conjuntos difusos a los que pertenecen [13].
Diseño de salidas difusas
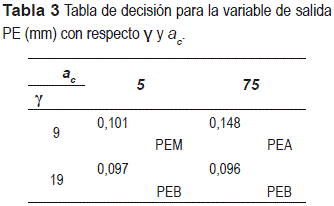
La salida posición del punto de estancamiento (PE) está en función de las variables de entrada ac y γ, al ser las únicas dos variables de entrada que presentaron un efecto significativo en PE. La tabla 3 es la tabla de decisión para la variable de salida PE (mm) con respecto γ y ac , los números difusos considerados son ''punto de estancamiento bajo'' (PEB), ''punto de estancamiento medio'' (PEM) y punto de estancamiento alto (PEA). En la tabla 3 implícitamente pueden apreciarse las reglas, que fueron obtenidas de acuerdo con las relaciones y los valores encontrados en la experimentación.
Reglas:
IF (γ IS 9) AND (ac IS 5) THEN (PE IS PEM).
IF (γ IS 9) AND (ac IS 75) THEN (PE IS PEA).
IF (γ IS 19) AND (ac IS 75) THEN (PE IS PEB).
La salida velocidad de la viruta (Vchip) depende de las tres entradas del modelo, pues las tres presentaron un efecto significativo en Vchip. Siendo entonces necesario fijar alguna de las tres entradas para el desarrollo de las reglas, en este caso se dejó fijo el ángulo de desprendimiento (γ). La tabla 4 es la tabla de decisión para la variable de salida Vchip (m/s), con γ = 9° y variando Vc y ac , los números difusos definidos son ''baja velocidad de la viruta'' (BVchip), ''velocidad de la viruta'' (Vchip), ''media velocidad de la viruta'' (MVchip) y ''alta velocidad de la viruta'' (AVchip).
Reglas:
IF (γ IS 9) AND (ac IS 5) AND (Vc IS 45) THEN (Vchip IS BVchip ).
IF (γ IS 9) AND (ac IS 5) AND (Vc IS 120) THEN (Vchip IS MVchip).
IF (γ IS 9) AND (ac IS 75) AND (Vc IS 120) THEN (Vchip IS AVchip ).
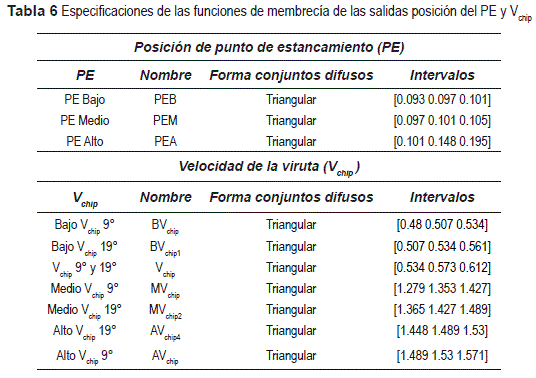
La tabla 5 es la tabla de decisión para la variable de salida Vchip, con γ = 19° y variando Vc y ac , las números difusos definidos son ''baja velocidad de la viruta uno'' (BVchip1), ''velocidad de la viruta'' (Vchip), ''media velocidad de la viruta dos'' (MVchip2) y ''alta velocidad de la viruta cuatro'' (AVchip4). En la tabla 6 se muestran las especificaciones de los conjuntos difusos en las funciones de membrecía.
Reglas:
IF (γ IS 19) AND (ac IS 5) AND (Vc IS 45) THEN (Vchip IS BVchip1).
IF (γ IS 19) AND (ac IS 5) AND (Vc IS 120) THEN (Vchip IS MVchip2).
IF (γ IS 19) AND (ac IS 75) AND (Vc IS 120) THEN (Vchip IS AVchip4).
Metamodelo con regresión lineal
Para comparar el metamodelo con lógica difusa se realizó un metamodelo adicional utilizando regresión lineal multivariable con Minitab [31]. La regresión realizada se expresa en las ecuaciones (2) y (3), para PE y Vchip respectivamente.
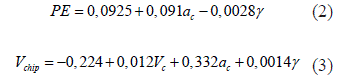
Discusión de resultados con los metamodelos
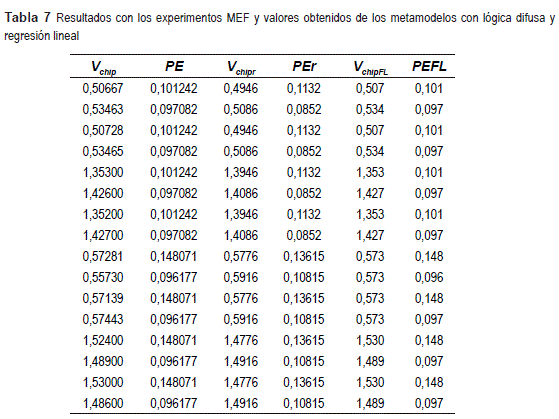
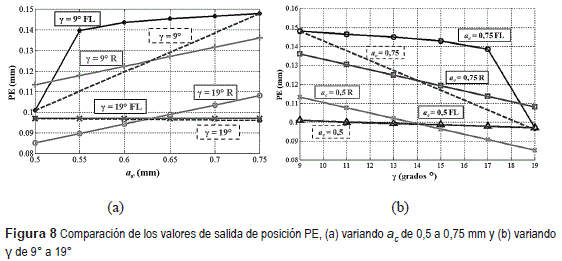
En la tabla 7 se presenta la comparación entre los valores experimentales de la simulación MEF con el metamodelo por lógica difusa y con el metamodelo por regresión lineal, donde velocidad de la viruta modelo MEF es Vchip, punto de estancamiento modelo MEF es PE, velocidad de la viruta modelo regresión es Vchipr, punto de estancamiento modelo regresión es PEr, velocidad de la viruta modelo FL es VchipFL, Punto de estancamiento modelo FL es PEFL. En la tabla 7 puede apreciarse que el modelo de lógica difusa es más preciso en los valores puntuales que la regresión y puede considerarse como una descripción cualitativa de los experimentos realizados.
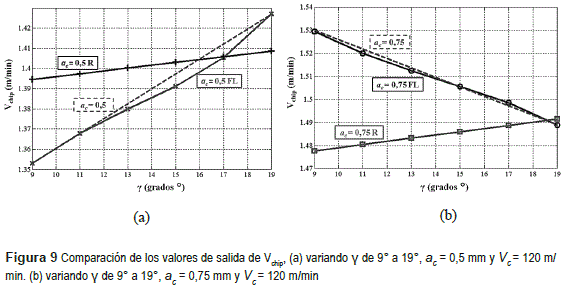
En las figuras 8 y 9 se puede observar un comportamiento más preciso del metamodelo por lógica difusa que el metamodelo regresión. En ambas figuras los valores obtenidos con la simulación MEF se muestran en línea punteada y las funciones de los metamodelos se identifican con FL (lógica difusa) y R (regresión). En el metamodelo con regresión se observan valores poco precisos, especificamente en la figura 9(b) donde la regresión se encuentra muy lejana de los valores experimentales además de presentar una pendiente contraria a la de la experimentación. El metamodelo por lógica difusa presenta en general un comportamiento más cercano a la experimentación.
Conclusiones
Se realizó un modelo MEF del proceso de maquinado aproximando el material de trabajo al flujo de un fluido muy viscoso e incompresible contra un cuerpo rígido que representaba la arista de corte. El comportamiento de la velocidad de flujo de la viruta fue similar al postulado por Trent [39]. De acuerdo con los resultados de las simulaciones, la densidad y la viscosidad del material de trabajo influyen también en la velocidad de flujo de la viruta, situación interesante que no se menciona en la teoría clásica.
De acuerdo a los resultados del diseño de experimentos en la simulación, la posición del punto de estancamiento solo dependería de las variables geométricas ac y γ. Esto no es consecuente con la realidad física mostrando una limitante en el modelo, pues se sabe por evidencia experimental que las propiedades del material de trabajo así como la velocidad de corte tienen una influencia importante en esta variable.
El empleo de metamodelos demostró ser una herramienta adecuada para encontrar una representación adecuada del proceso, de una forma rápida y económica. El metamodelo con lógica difusa mostró un comportamiento general acorde con los resultados de los experimentos MEF. De otro lado el metamodelo usando regresión numérica, es poco exacto en los valores puntuales de las salidas.
Debido a que el software MEF utilizado (Ansys), no permite modificar las variables esfuerzo, deformación y temperatura, no es posible ajustar mejor el modelo propuesto. De hecho usar un fluido incompresible, produce una homogenización del volumen de control y no permite la simulación de estas variables. El modelo propuesto no incluyó la interacción viruta - herramienta, la cual es fundamental en el estudio del proceso de maquinado por la altísima fricción presente y la consecuente formación de la llamada zona de cizallamiento secundaria.
Las mencionadas limitaciones del modelo se evidencian por la influencia casi exclusiva de las variables geométricas, y una muy baja sensibilidad con respecto a las propiedades del material de trabajo. Por lo expuesto, es necesario continuar trabajando en esta propuesta inicial para incluir la simulación y modificación dinámica de las variables esfuerzo, deformación y temperatura así como la interacción viruta - herramienta.
Referencias
1. M. Shaw. ''Introduction''. Metal Cutting Principles. 2nd ed. Ed. Oxford University Press. New York, US. 2005. pp. 1-8. [ Links ]
2. E. Trent, P. Wright. ''Introduction: Historical and Economic Context''. Metal Cutting. 4th ed. Ed. John Wiley & Sons Inc., Butterworth-Heinemann. Oxford, UK. 2000. pp. 1-8. [ Links ]
3. V Astakhov. ''Tribology of Metal Cutting''. Tribology and Interface Engineering Series. Vol. 52. 2006. pp. 1-43. [ Links ]
4. M. Cakir, K. Cavdar. ''Development of a knowledge- based expert system for solving metal cutting problems.'' Materials & Design. Vol. 27. 2006. pp. 1027-1034. [ Links ]
5. V Astakhov. ''Introduction''. Metal Cutting Mechanics. 1st ed. Ed. CRC Press LLC. New York, US. 1998. pp. 1-9. [ Links ]
6. T. Childs, K. Maekawa, T. Obikawa, Y. Yamane. ''Chip formation fundamental.'' Metal Machining Theory an applications. 1st ed. Ed. Arnold Publishers. 2000. London, England. pp. 35-80. [ Links ]
7. H. Ernst, M. Merchant. ''Chip formation, friction and high quality machining surface on surface treatment of metals''. American Society of Metals. Vol. 29. 1941. pp. 299-378. [ Links ]
8. M. Merchant. ''Mechanics of the metal cutting process.'' J. Appl. Phys. Vol. 16. 1945. pp. 318-324. [ Links ]
9. X. Wang, I. Jawahir. ''Recent advances in plasticity applications in metal machining: slip-line models for machining with rounded cutting edge restricted contact grooved tools.'' International Journal ofMachining and Machinability of Materials. Vol. 2. 2007. pp. 347-360. [ Links ]
10. D. Montgomery. Design and Analysis of Experiments. 5th ed. Ed. John Wily and Sons. New Jersey, US. 2001. pp. 1-19. [ Links ]
11. O. Zienkiewicz, R. Taylor. The Finite Element Method. 8th ed. Ed. Butterworth-herinemann. Boston, US. 2000. pp. 1-84. [ Links ]
12. U. Dixit, P. Dixit. ''Predictive Modeling of Metal Forming and Machining Processes Using Soft Computing''. Modeling of Metal Forming and Machining Processes - by Finite Element and Soft Computing Methods. 1st ed. Ed. Springer. New Delhi, India. 2008. pp. 503-547. [ Links ]
13. G. Bojadziev, M. Bojadziev. Fuzzy set, Fuzzy logic, Application. 1st ed. Ed. World Scientific Publishing Co.. Singapore. 1998. pp. 117-206. [ Links ]
14. M. Dirikolu, T. Childs, K. Maekawa. ''Finite element simulation of chip flow in metal machining.'' International Journal of Mechanical Sciences. Vol. 43. 2001. pp. 2699-2713. [ Links ]
15. J. Mackerle. ''Finite-element analysis and simulation of machining: a bibliography (1976-1996)''. Journal of Materials Processing Technology. Vol. 86. 1998. pp. 17-44. [ Links ]
16. J. Mackerle. ''Finite element analysis and simulation of machining: an addendum: A bibliography (1996-2002)''. International Journal of Machine Tools and Manufacture. Vol. 43. 2003. pp. 103-114. [ Links ]
17. O. Zienkiewicz. ''Chapter 18''. The Finite Element Method in Engineering Science. 2nd ed. Ed. McGraw- Hill. London, England. 1971. pp. 551. [ Links ]
18. E. Usui, K. Maekawa, T. Shirakashi. ''Simulation analysis of cutting fluid action''. J. Japan. Soc. Prec. Eng. Vol. 43. 1977. pp. 1063-1068. [ Links ]
19. V. Astakhov, J. Outeiro. ''Metal Cutting Mechanics, Finite Element Modelling''. Machining. 1st ed. Ed. Springer. London, England. 2008. pp. 1-28. [ Links ]
20. T. Childs, K. Maekawa, T. Obikawa, Y. Yamane. ''Finite Element Methods''. Metal Machining Theory an applications. 1st ed. Ed. Arnold Publishers. London, England. 2000. pp. 199-225. [ Links ]
21. H. Bil, S. KIlIç, A. Tekkaya. ''A comparison of orthogonal cutting data from experiments with three different finite element models''. International Journal of Machine Tools and Manufacture. Vol. 44. 2004. pp. 933-944. [ Links ]
22. V. Marinov. ''Hybrid analytical-numerical solution for the shear angle in orthogonal metal cutting—Part I: theoretical foundation''. International Journal of Mechanical Sciences. Vol. 43. 2001. pp. 399-414. [ Links ]
23. V. Astakhov, M. Osman, M. Hayajneh. ''Re-evaluation of the basic mechanics of orthogonal metal cutting: velocity diagram, virtual work equation and upper- bound theorem''. International Journal of Machine Tools and Manufacture. Vol. 41. 2001. pp. 393-418. [ Links ]
24. D. Montgomery. ''Two-Level Fractional Factorial Designs''. Design and Analysis of Experiments. 5th ed. Ed. John Wily and Sons. New Jersey, US. 2001. pp. 303-362. [ Links ]
25. G. Giorleo, R. Teti, U. Prisco, D. D'Addona. ''Merging Neural Network Material Rheological Behaviour Modelling with FEM - Simulation of Orthogonal Metal Cutting''. Machining Science and Technology: An International Journal. Vol. 7. 2003. pp. 401-417. [ Links ]
26. M. Shaw. ''Shear Stress in Cutting''. Metal Cutting Principles. 2nd ed. Ed. Oxford University Press. New York, US. 2005. pp. 142-153. [ Links ]
27. V. Venkatesh, S. Izman. ''Mechanics of Materials Cutting.'' Precision engineering. 1st ed. Ed. McGraw- Hill. New Delhi, India. 2007. pp. 80-107. [ Links ]
28. M. Jackson. ''Mechanical Micromachining''. Micro and Nanomanufacturing. 1st ed. Ed. Springer. New York, US. 2007. pp. 191-254. [ Links ]
29. K. Fang, R. Li, A. Sudjianto. Design and modeling for computer experiments. 1st ed. Ed. Chapman & Hall/ CRC. London, England. 2006. pp 3-65. [ Links ]
30. J. Posta, G. Klaseboera, E. Stinstra, T. van Amstel, J. Huetink. ''Multi-stage metal forming: Variation and transformation''. Journal of Materials Processing Technology. Vol. 209. 2009. pp. 2648-2661. [ Links ]
31. D. Montgomery. ''Fitting Regression Models''. Design and analysis of experiments. 5th ed. Ed. John Wily and Sons. New Jersey, US. 2001. pp. 392-426. [ Links ]
32. The MathWorks, Inc. Fuzzy Logic Toolbox™ User's Guide. © COPYRIGHT 1995-2008 The MathWorks, Inc. Natick, US. 2008. pp. 1-345. [ Links ]
33. I. Shames. ''Flujo viscoso incompresible general: Las ecuaciones de Navier-Stockes''. Mecánica de fluidos. 3rd ed. Ed. McGRAW-HILL. Bogotá D. C., Colombia. 1995. pp. 397-430. [ Links ]
34. T. Childs, K. Maekawa, T. Obikawa, Y. Yamane. '' Work material: Typical mechanical and thermal behaviours, Appendices''. Metal Machining Theory an applications. 1st ed. Ed. Arnold Publishers. 2000. London, England. pp. 375-380. [ Links ]
35. M. Shaw. ''Plastic Behavic''. Metal Cutting Principles. 2nd ed. Ed. Oxford University Press. New York, US. 2005. pp. 45-78. [ Links ]
36. D. Montgomery. ''The 2k Factorial Design''. Design and Analysis of Experiments. 5th ed. Ed. John Wily and Sons. New Jersey, US. 2001. pp. 218-287. [ Links ]
37. International Nickel Company. Properties of some metals and alloys: chemical composition/mechanical properties/physical properties/specifications/sources of additional information. International Nickel Company of Canada (editor). Development and Research Division. New York, US. 1968. pp. 1-62. [ Links ]
38. E. Ceretti, M. Lucchi, T. Altan. ''FEM simulation of orthogonal cutting: serrated chip formation''. Journal of Materials Processing Technology. Vol. 95. 1999. pp. 17-26. [ Links ]
39. E. Trent, P. Wright. ''Machinability''. Metal cutting. 4th ed. Ed. John Wiley & Sons Inc., Butterworth-Heinemann. Oxford, UK. 2000. pp. 251-310. [ Links ]
40. G. Boothroyd, W. Knight.Fundamentals of Machining and Machine tools. 2nd ed. Ed. CRC Press. New York, US. 1989 pp. 1-59. [ Links ]
41. S. Choi, R. Grandhi, R. Canfield. Reliability-based structural design. 1st ed. Ed. Springer. London, England. 2007. pp 1-7. [ Links ]
42. M. El Baradie. ''A fuzzy logic model for machining data selection''. International Journal of Machine Tools and Manufacture. Vol. 37. 1997. pp. 1353-1372. [ Links ]
43. K. Hashmi, M. El Baradie, M. Ryan. ''Fuzzy-logic based intelligent selection of machining parameters''. Journal of Materials Processing Technology. Vol. 94. 1999. pp. 94-111. [ Links ]
44. K. Hashmi, I. Graham, B. Mills, M. Hashmi. ''Adjustment approach for fuzzy logic model based selection of non-overlapping machining data in the turning operation''. Journal of Materials Processing Technology. Vol. 142. 2003. pp. 152-162. [ Links ]