ARTÍCULO ORIGINAL

Acumulación de daño y redistribución de los esfuerzos en materiales reforzados con fibras

Damage accumulation and redistribution of stresses in fiber reinforced material

Anatoli S. Ovchinsky¹, Pedro Tamayo Meza^2*, Juan M. Sandoval-Pineda², Luis A. Flores-Herrera², Alejandro Álvarez Zapata²

¹Instituto de Metalurgia, Academia de Ciencias de Rusia, Lenninsky Prozpekt 49, Moscú, Rusia.

²Laboratorio de Fuerza Atómica. Sección de Estudios de Posgrado. Escuela Superior de Ingeniería Mecánica y Eléctrica. Instituto Politécnico Nacional. Av. de las Granjas, N°.682, Delegación Azcapotzalco, C.P. 02250, México, DF.

^*Autor de correspondencia: teléfono: + 55 + 7296000, ext. 64503, correo electronico: ptamayom@ipn.mx (P. Tamayo)

(Recibido el 28 de agosto de 2012. Aceptado el 11 de octubre de 2013 )

Resumen

Se analiza el proceso de fractura de materiales compuestos, considerando la interacción de diferentes factores que tienen un carácter muy particular. La resistencia a la ruptura de las fibras, la resistencia localizada de la matriz y la fuerza de adherencia entre la fibra y la matriz, por lo general varían de manera substancial y, además, la distribución del reforzamiento es errática y casual. Analíticamente la interacción entre estos imprevisibles factores durante la fractura del compuesto no pueden ser plenamente descritos mediante el uso de métodos probabilísticos. El desarrollo de métodos computacionales abre enormes posibilidades para simular la influencia de estos factores durante el proceso de fractura del compuesto. Determinadas dificultades surgen en el desarrollo de estas investigaciones porque éstas sintetizan problemas de física de materiales, así como de mecánica al tener que considerar y analizar simultáneamente la estructura real del material. Por lo anterior, resulta conveniente junto con la simulación numérica aplicada al estudio de determinados fenómenos y a la solución de problemas prácticos, hacer uso de criterios que son fundamentales para simular los procesos de delaminación de las fibras fracturadas y el desarrollo de grietas en la matriz.

Palabras clave: Fractura, interfase, delaminación, fibras, matriz

Abstract

During the analysis of fracture processes of composite materials we deal with the interaction of different factors that have a very particular character. There exist a substantial variation between the breaking resistance of the fibers, the resistance of the matrix and the adhesion resistance of the matrix, as well as the arrangement of the reinforcement which is erratic and random. The unpredictable interaction between these factors during the fracture of the compound is not fully described by using probabilistic methods. The development of computational methods opens an enormous amount of possibilities to simulate the influence of these factors during the fracture process of the composite. The use of computational methods is complex because the algorithms must synthesize both physical and mechanical problems of materials considering at the same time the real structure of the materials. Because of that, the use of fundamental criteria is suitable in order to create the simulation of the delamination processes in cracked fibers and the development of cracks in the matrix.

Palabras clave: Fracture, interface, delamination, fiber, matrix

Introduction

El rompimiento de algunas fibras en el compuesto conduce a una sobrecarga de las fibras circundantes, así como al surgimiento de esfuerzos tangenciales en la interfase, y a un incremento de la intensidad del esfuerzo en micro volúmenes adyacentes. La propagación de la fractura a nivel micro estructural puede darse por rompimiento de las fibras circundantes, por delaminación (exfoliación) de la fibra, así como por el desarrollo de grietas en la matriz. Considerando que la simulación numérica de experimentos en computadores se utiliza con amplitud en la física metalúrgica, no son muchos los trabajos en el campo de la modelación del proceso de fractura de materiales compuestos a nivel micro estructural.

Durante la simulación de materiales compuestos con fibras frágiles, las fibras se multi fragmentan [1]. El análisis de los procesos de redistribución de los esfuerzos y su dinámica demostró que las fibras suelen romperse, fragmentándose tanto en trozos inferiores a la longitud crítica (como resultado de la acción de las ondas de sobrecarga), así como en trozos significativamente superiores al crítico (por delaminación de la matriz). Sin embargo, a pesar de la diversidad de situaciones que surgen durante el rompimiento de las fibras, el mecanismo fundamental que interviene para que las fibras fracturadas aporten al trabajo, es la redistribución del esfuerzo entre ellas mediante las deformaciones de corte, y las correspondientes tensiones tangenciales en la matriz. Debido a esto, como elemento estructural del material compuesto se considera el trozo de fibra rodeada con matriz adherida a él, cuya longitud es el doble de la longitud que transfiere la carga l_c(min), determinada en el supuesto de que los componentes del sistema se deforman elásticamente.

Es fundamental estimar la longitud crítica de la fibra. Como se muestra en la ecuación 1, ésta depende de la relación entre la rigidez de los componentes E = E_f / G_m, y sus fracciones de volumen b≈0.95(1 -V_f), y que conforme a z_p(min) =1.63 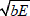.d_f, donde b es la distancia entre las fibras, parámetro adimensional que se determina como: 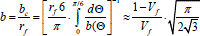, y que para una serie de casos aproximadamente es: b = 0,955(1 - V_f)/V_f ≈ (1 - V_f)/V_f, entonces la longitud crítica l_c(min) se puede determinar como se muestra en la ecuación 1.

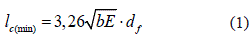
Estimar la mínima longitud crítica permite relacionar la resistencia de las fibras originales con la resistencia de los segmentos cortos de fibras en el compuesto, que designaremos como l_c.

Modelos estructurales de compuestos con fibras frágiles

En la simulación de compuestos con fibras frágiles en primer lugar se considera que las fibras se fracturan reiteradamente.

El análisis de los procesos de redistribución de los esfuerzos, procesos dinámicos, demostró que las fibras pueden romperse, fragmentándose en trozos inferiores a la longitud crítica como resultado del efecto de una onda de sobrecarga, así como en trozos significativamente mayores al desprenderse de la matriz. A pesar de las diferentes situaciones que surgen durante el rompimiento de las fibras, el mecanismo fundamental que incorpora al trabajo a las fibras fracturadas es la redistribución del esfuerzo entre ellas mediante las deformaciones de corte y los correspondientes esfuerzos tangenciales en la matriz. En consecuencia, como elemento estructural consideramos un trozo de fibra con matriz adherida él, cuya longitud es el doble de la longitud de transferencia de la carga l_c(min), suponiendo que los componentes se deforman elásticamente (1).

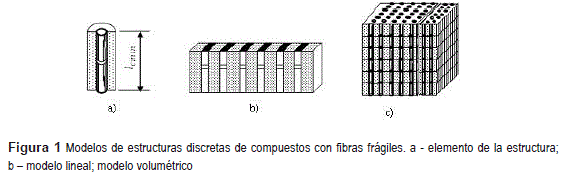
Se analizó una fibra con longitud crítica para construir un modelo analítico de rompimiento de material compuesto [2, 3]. Sin embargo, la construcción de modelos discretos de compuestos supone que el elemento seleccionado posee una resistencia ideal, y tiene una zona defectuosa localizada, es decir, se predefine un posible lugar para el rompimiento de la fibra, figura 1a. Arreglando los elementos de diferente manera, se propone un modelo que refleja la estructura del material compuesto con distintos grados de aproximación. Combinando en serie estos elementos, o bien, conectándolos en paralelo, se puede obtener sencillos modelos lineales o unidimensionales de compuestos. Análogamente, es posible construir dos variantes de modelos planos o bidimensionales, que simulan tanto el ensamble de las fibras en el área transversal del material, figura 1b, así como su estructura a lo largo de ellas. Es lógico imaginar, que tanto los modelos lineales y planos son variantes simplificadas de modelos tridimensionales, que simulan una distribución de los elementos estructurales en materiales compuestos reales, figura 1c. La construcción de un modelo lineal, plano o tridimensional está determinada por los objetivos y los problemas que se asignan para la simulación de los procesos de fractura. Estos mismos factores determinan la distribución de los defectos en los vértices donde se acoplan los elementos, o la simulación de los puntos de su disposición dentro de éstos. El análisis de estos defectos puede llevarse a cabo utilizando simplificados modelos lineales o planos, y los tridimensionales en la mayoría de los casos son poco recomendables. Por esta razón, resulta efectivo el desarrollo de un modelo cuasi - volumétrico, en el cual es posible rastrear el desarrollo de la fractura en una determinada área del material, pero en donde se toman en cuenta los procesos que se desarrollan en el volumen circundante, por ejemplo, la delaminación,figura 1c.

Redistribución de la resistencia en fibras de segmentos cortos

Con los resultado de los ensayos de tensión de las fibras, construimos una función de densidad de la probabilidad g(σ_fb), o bien una distribución de la probabilidad G(σ_fb) de que las fibras se rompan en un cierto rango de esfuerzo. La resistencia de las fibras frágiles está determinada por la presencia de defectos, cuya distribución según su intensidad depende de su longitud. Debido a esto, si las funciones originales g(σ_fb) y G(σ_fb) fueron construidas durante el ensayo de una fibra con longitud L_f, entonces éstas funciones caracterizan la resistencia de una fibra con sus correspondientes dimensiones. Pero en la simulación numérica de un modelo de compuesto se requiere conocer cómo se distribuye la resistencia en los trozos cortos de fibra con longitud crítica l_c(min). Para ello simulamos las fibras como una cadena compuesta de n_f eslabones, donde n_f = L_f / l_c(min) [2].

Si F (G_fb) es la distribución de probabilidad de que se rompa un eslabón de la cadena, entonces la probabilidad de que no se rompan todos los n_f eslabones es [1 - F(σ_fb)] n_f , y significa que no existe ninguna probabilidad de que se rompa toda la cadena [1 - G(σ_fb)].

Como resultado de esto, se obtuvo una función que relaciona la probabilidad de rompimiento de algunos trozos separados de fibra de longitud l_{c min}, con la probabilidad de fractura de una fibra de longitud L_f, ecuación 2:

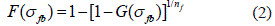
El enlace de las funciones diferenciales de distribución de la resistencia de los trozos cortos de fibras f(σ_fb), y las fibras con longitud inicial se puede expresar entonces mediante la ecuación 3:

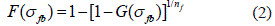
Destacamos, que para grandes valores de L_f / l_c(min), es decir, para grandes n_f, la distribución f(σ_fb) tiene un carácter claramente pronunciado, y la transición, ecuación 2, evidencia muy bien el efecto de escala solamente en aquel rango de magnitudes, donde se expresa claramente la función de la resistencia respecto a su longitud [4, 5].

Por lo tanto, cuando se utilizan las Ecuaciones 2 y 3, es necesario evaluar no solo l_c(min), sino que también L_f , es decir, aquella longitud de la fibra que después de los ensayos la información estadística puede ser la base para ulteriores cálculos. Determinar esta longitud extrema es posible en base al análisis estadístico de las funciones experimentales del promedio de la resistencia de la fibra respecto a sus dimensiones. Es posible emplear los datos experimentales de los ensayos de tensión sobre una fibra con longitud estándar, pero para determinar n_f = L_f / l_c(min), se requiere que en lugar de L_f, emplear un tamaño sustituto cercano a la longitud extrema, por encima de la cual el efecto de escala resulta menos ostensible.

Para un análisis más acertado se sugiere colocar la distribución inicial de la resistencia sobre fibras con longitud más reducida; éstas se aproximan mejor a la distribución de la resistencia de fibras con longitud crítica y de forma más precisa se reacomodan en él.

Aproximación estadística de distribución de la resistencia. Expresión analítica

Para describir la distribución estadísticamente de la resistencia de la fibra, por lo general se emplean las funciones de Weibull, ecuación 4 y 5:

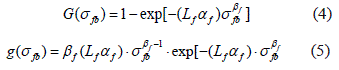
El parámetro α_f está asociado con el promedio de la resistencia 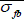de una fibra y se expresa mediante la ecuación 6:

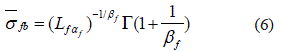
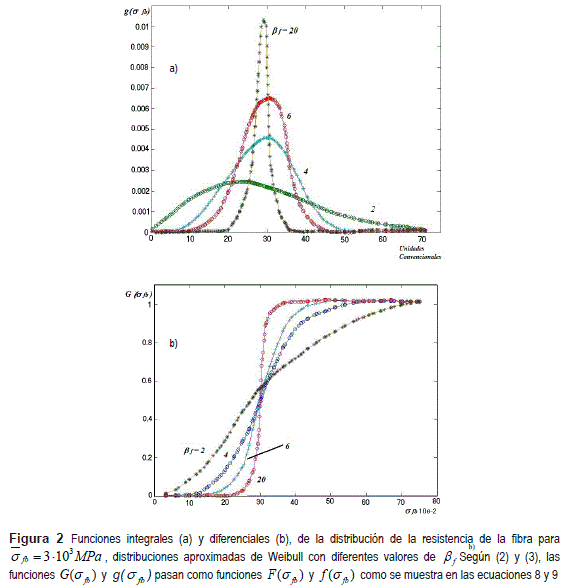
Donde: Γ(....) es una γ función. El parámetro β_f, que caracteriza la dispersión de la resistencia, se relaciona con la dispersión de la distribución mediante la función expresada en la ecuación 7

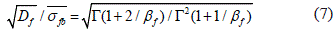
En la figura 2, se muestran el comportamiento de las leyes de Weibull de distribución de la resistencia para fibras con , y distintos valores del parámetro β_f.

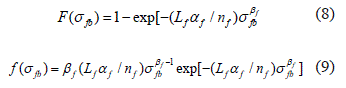
Utilizando la función (6), la expresión (9) toma la forma de la ecuación 10:

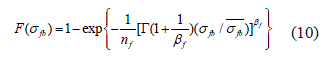
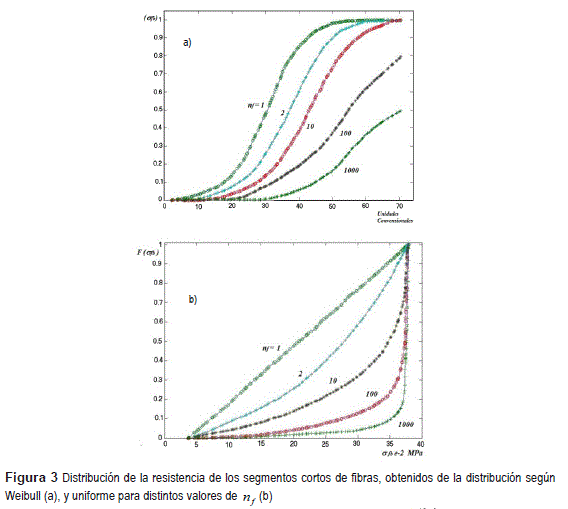
En la figura 3, se muestran los cambios característicos de las funciones f(σ_fb) y F(σ_fb) en relación con la magnitud de n_f. Señalamos, que el uso de la transformada de la ecuación 2, aplicada a la distribución de la resistencia según Weibull, nos lleva a un incremento considerable de la resistencia al aumentar n_f. Una naturaleza fundamentalmente diferente en el cambio de la función de distribución se observa, si la distribución estadística de la resistencia la aproximamos a una distribución confinada, por ejemplo, uniforme en el intervalo 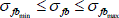y 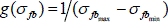. El uso de las ecuaciones 2 y 3, aplicadas a una distribución uniforme conduce a un cambio cualitativo del tipo de distribución estadística, y a un mínimo incremento de la resistencia de la fibra, tendiente a σ_fbmax, al disminuir su longitud, figura 3.

Simulación numérica de los valores aleatorios de la resistencia; discusión del problema

Existen varias definiciones del método de Monte Cario, o modelación estadística [6, 7], En particular, así denominan los métodos que emplean números aleatorios [8], Sin embargo, ''números aleatorios'' es un concepto bastante indefinido, porque si se dispone de una secuencia de números aleatorios, entonces en ellos es posible establecer algunas regularidades. En la práctica no se requiere disponer de una secuencia de números verdaderamente aleatorios. Si en relación a algún uso concreto la ley es insignificante, entonces para una aplicación dada los números se consideran aleatorios [8].

Justamente en este principio nos basamos para el uso de programas estándares que contienen el moderno software matemático, y que permiten generar números pseudo aleatorios [9]. En nuestro caso empleamos subprogramas estándares generadores de números aleatorios uniformemente distribuidos en un intervalo de [0,1]. Cada vez que se requirió el uso del programa se elaboró un número aleatorio íK. Entonces disponiendo de números aleatorios uniformemente distribuidos, es posible generar y otros tipos de distribuciones, por ejemplo, la requerida función F(σ_fb).

Uno de los métodos en que nos basamos para obtener los valores aleatorios de la resistencia consistió en que igualamos las dos funciones de distribución, como se muestra en la ecuación 11:

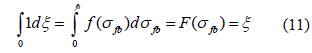
Si se puede determinar F^*(ξ), que es el inverso de F(σ_fb), entonces el valor aleatorio de la resistencia se puede determinar según la ecuación 12:

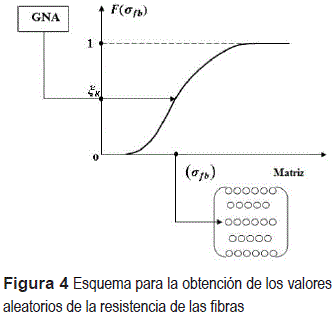
En la figura 4, señalamos cómo obteniendo los números aleatorios ξ_k en el intervalo de 0 a 1, y empleando el gráfico de una función integral de distribución de la resistencia, es posible encontrar el valor aleatorio correspondiente de la resistencia de las fibras [10].

GNA - Generador de números aleatorios

Basándose en la expresión analítica F(σ_fb) para la distribución de los defectos según su intensidad, relacionados con la longitud del elemento estructural, ecuación 10, obtenemos para él una expresión para los valores aleatorios de la resistencia de la fibra en áreas dañadas empleando la ecuación 13:

Sustituyendo en lugar de F(σ_fb) los números aleatorios ξ_k, uniformemente distribuidos en el intervalos de 0 a 1, mediante la Ecuación 13, obtenemos los valores aleatorios de la resistencia de las fibras para una distribución predeterminada, figura 4. A partir de estos valores de la resistencia en el computador se generan matrices numéricas unidimensionales, bidimensionales y tridimensionales, correspondientes al modelo discreto propuesto de material compuesto, como se exhibió en la figura 1 [11].

Alteración en la capacidad de carga

El rompimiento de las fibras altera la capacidad de carga del material compuesto. Para simular la carga aplicada sobre un modelo de material compuesto, se requiere determinar la acumulación de fracturas en los lugares defectuosos de la fibra. La carga axial P_c , que soporta cada capa del compuesto fragmentado hasta alcanzar longitudes críticas, cuya magnitud axial es la mínima longitud crítica l_cmin , incluye la carga que soporta un volumen sin defectos C_σF_σ, un volumen con defecto , y una carga adicional Δσ_LF_L que soporta el volumen sin defectos resultante de la redistribución del esfuerzo. Entonces podemos plantear la ecuación 14:

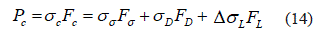
La tensión media en el compuesto σ_c se puede determinar entonces según la ecuación 15:

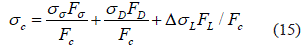
El área de los volúmenes con defectos F_D, es proporcional a la cantidad de elementos dañados en una determinada capa, y la superficie relativa F_D /F_C es igual a la relación del número de fibras fracturadas en la capa entre el número total de fibras. El número de fibras fracturadas en la capa crece a medida que se incrementa el esfuerzo, y su proporción relativa en un determinado volumen puede oscilar entre 0 a 1. Esta circunstancia permite introducir una función de acumulación de daño W(σ_f). que es la relación entre la cantidad de fibras dañadas en la capa, y la cantidad total de fibras, y caracteriza el incremento de la superficie relativa de áreas defectuosas en la sección de material simulado, y que la expresamos como en la ecuación 16:

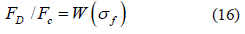
Entonces la superficie relativa del área sin lugares defectuosos es, como en la ecuación 17:

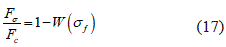
El área de la sección transversal de los volúmenes sobretensionados también es proporcional a la cantidad de fibras fracturadas en las capas, y la podemos expresar a través de la ecuación 18:

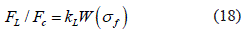
Entonces colocando las ecuaciones (16), (17) y (18) en la ecuación (15), obtenemos la ecuación 19:

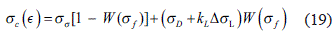
La ecuación 19, podemos analizarla como si fuera el diagrama de esfuerzo - deformación para un compuesto con fibras unidireccionalmente orientadas, puesto que σ_σ es la capacidad de carga de volúmenes sin defectos, y se determina empleando la ecuación de las mezclas, ecuación 20.

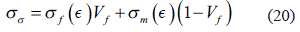
Similar a la regla de las mezclas, podemos expresar la capacidad de carga de los volúmenes dañados σ_D, y las cargas adicionales Δ σ_p , pero con unos coeficientes de mediación que reflejan las irregularidades localizadas del estado de esfuerzo, ecuaciones 21 y 22:

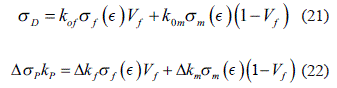
Donde los coeficientes k_of, k_0m, Δk_f y Δk_m - reflejan la carga relativa percibida por los segmentos anulares de las fibras fracturadas, de la matriz, sus circundantes, por las fibras vecinas y la matriz que los envuelve, por ejemplo, en la ecuación 23:

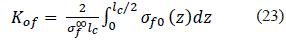
Donde: σ_f0(z) es la distribución axial del esfuerzo a lo largo de la fibra fracturada.

La introducción de estos coeficientes permite evaluar la capacidad de carga de los volúmenes dañados del material simulado, y considerar las particularidades de la interacción mecánica de los componentes. Estos coeficientes se determinan en base a un modelo, así como de la algoritmización de los procesos de redistribución del esfuerzo.

Fragmentación de la fibra: Simulación numérica

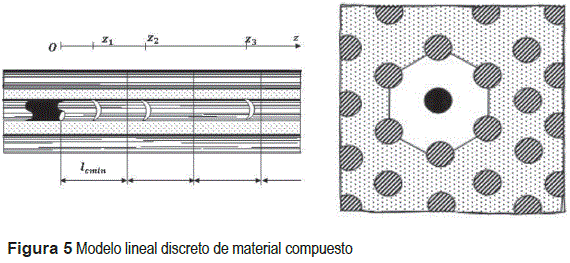
Las circunstancias relacionadas con la fragmentación de la fibra han sido analizadas ampliamente [12-14]. El impacto de los efectos dinámicos sobre la fragmentación de la fibra puede estudiarse con ayuda de un sencillo modelo lineal de compuesto, consistente en una fibra con asientos defectuosos casualmente distribuidos, y una perturbación generada bajo un determinado esfuerzo σ_f^∞ en un momento inicial t = 0, figura 5.

Suponemos, que las fibras vecinas se hayan en estado de tensión uniforme, correspondiente a un nivel de esfuerzo primario de fractura σ_f^∞. Entonces la fibra se parte en segmentos de longitud crítica mínima l_c(min). También suponemos, que en cada tramo de longitud crítica hay por lo menos un defecto casual. La intensidad de distribución de estos defectos se puede describir mediante la Ecuación 10. Como inicio de las coordenadas consideramos el lugar de la rotura primaria. Las coordenadas de los defectos podemos representarlo como en la ecuación 24

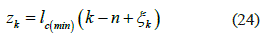
Donde: k = 1, 2, 3,..... , n es el número del próximo defecto, ξ_k - números aleatorios uniformemente distribuidos en el intervalo de 0 a 1.

En la memoria del computador se forman matrices unidimensionales de números que caracterizan los valores de las coordenadas de los defectos z₁, z₂,…….z_n, y valores al azar de la resistencia de la fibra en los sitios con defectos (σ_fb1), (σ_fb2),……. (_fbn), que se obtienen conforme con la ecuación 13. Una peculiaridad del modelo que proponemos consiste en que de los valores aleatorios de la resistencia, ecuación 13, se seleccionaron solamente aquellos que son mayores que σ_f^∞ - umbral del esfuerzo de la rotura primaria.

La transición de la etapa de acumulación de daño al desarrollo de una grieta magistral o macro fractura, ocurre como resultado de la interacción de diferentes mecanismos de fractura. La simulación numérica del proceso de fractura consiste en que a partir de valores aleatorios de la resistencia de la fibra σ_fb, obtenidos según la ecuación 13, en la memoria del computador generamos una matriz bidimensional de cifras que reflejan los valores de la resistencia de la fibra y su ubicación en una determinada área del material. En la figura 5, mostramos un fragmento del material con distribución hexagonal de las fibras.

El proceso real de fractura secuencial de las fibras en el área transversal que va acompañado de una redistribución del esfuerzo, es un problema extraordinariamente complejo para su esquematización. La redistribución del esfuerzo ocasiona el rompimiento de las fibras sobre tensionadas, éstas generan una segunda redistribución, éstas una tercera, y así sucesivamente. La dificultad en la esquematización reside en que, por lo general, es imposible separar los procesos que suceden en forma paralela y consecutivamente, y en los fenómenos que transcurren simultáneamente y de manera secuencial [15, 16].

Se considera, que durante la fractura de las fibras separadas la carga se redistribuye a las seis fibras vecinas, cuando el ordenamiento es hexagonal. El esfuerzo en las fibras, vecinas a la fracturada (en el área transversal), experimenta un incremento k_f1σ_fi, donde σ_fi es el esfuerzo de ruptura de una i fibra, y k_f1 es el coeficiente de transferencia de carga, que considera la fracción de volumen de los componentes, y la relación de sus propiedades elásticas y plásticas, se determina mediante la ecuación 25:

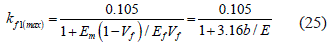
El rompimiento de las fibras individuales conduce a una sobrecarga de las vecinas, así como al surgimiento de esfuerzos tangenciales en la interfase y a un incremento de la intensidad del esfuerzo en micro volúmenes adyacentes de la matriz. El posterior desarrollo del proceso de fractura a nivel micro estructural puede darse por rompimiento de las fibras vecinas, por delaminación de la fibra fracturada, y por el desarrollo de grietas en la matriz. Considerando esta circunstancia, en las simulaciones posteriores junto con la generación de una matriz numérica, que describe los valores aleatorios de la resistencia de la fibra σ_fb, se generaron matrices de números que caracterizan valores aleatorios de los micro volúmenes de la matriz, adyacentes a las zonas dañadas de la fibra σ_mb, y valores aleatorios en la resistencia al corte de la adherencia τ_jb así como en los sitios de posibles rompimientos de las fibras. La simulación de los procesos de delaminación de las fibras fracturadas requiere de la algoritmizacion de este micro mecanismo de fractura y el desarrollo de los correspondientes criterios. Por esta razón es importante considerar las siguientes circunstancias.

Inicio de la exfolicación

Si los máximos esfuerzos tangenciales τ_max en los lugares donde se rompe la fibra superan a los valores localizados de la resistencia al desprendimiento τ_jb entonces se considera la desigualdad 26:

y la fibra fracturada comienza a desprenderse de la matriz.

Empleando la relación para los máximos esfuerzos tangenciales en la etapa cuando la matriz se deforma elásticamente, la exfoliación comienza cuando se tienen las condiciones mostradas en la ecuación 27:

y cuando la deformación al corte de la matriz es elástico-plástica, se tiene entonces la ecuación 28:

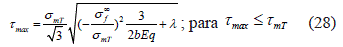
Dónde: σ_mT= 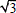τ_mT y λ=(q-1)/q. Cuando el comportamiento de la matriz es plástico - elástico, las máximas tensiones tangenciales decrecen con el tiempo, conforme a: 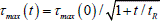. Entonces la exfoliación se inicia cuando σ_fb> σ_fτ. Las funciones (26) y (27) pueden analizarse como criterio, porque SI τ_max≥τ_jb donde τ_jb es el valor local de la resistencia al corte de la interfase en un lugar dado, a continuación del rompimiento de la fibra ocurre su desprendimiento de la matriz.

La fibra comienza a fracturarse

Si los valores máximos de la intensidad del esfuerzo en la matriz σ_(mi(max), adyacente al punto de ruptura de la fibra, exceden los valores localizados de resistencia de la matriz σ_(mb,σ_(mi(max)>σ_mb, entonces después de la fractura de la fibra sobreviene el rompimiento de los micro volúmenes adyacentes en la matriz. Utilizando las funciones para los valores máximos de la intensidad del esfuerzo en la matriz, se dan 4 posibles soluciones, que se muestran en el conjunto de ecuaciones 29:

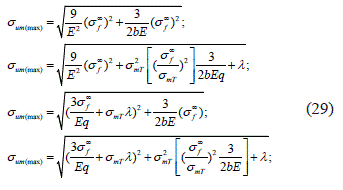
en función de la fracción de volumen, y de la relación de las propiedades elásticas de los componentes, así como en función del nivel de los esfuerzos σ_f^∞, los valores máximos de la intensidad del esfuerzo en la matriz, adyacente al punto de ruptura de la fibra.

Durante la simulación del desprendimiento de la fibra y el desarrollo de grietas en la matriz, es necesario evaluar la longitud de los segmentos delaminados y la profundidad de las grietas surgidas en la matriz.

Prolongación de zona exfoliada de la fibra fracturada

Para determinar la longitud de la zona exfoliada se requiere de una representación dinámica, en el cual el segmento exfoliado de fibra durante su desplazamiento es afectado por una fuerza de roce de intensidad constante, y considerando la intensidad del esfuerzo en la matriz, se tiene la ecuación 30.

que es la intensidad de la deformación en la matriz; entonces la extensión de la zona exfoliada se puede determinar por la ecuación 31:

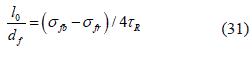
En la simulación de los procesos de delaminación en algunos casos es fundamental la relación l₀ entre la mínima longitud crítica l_c(min), entre la longitud del elemento estructural. Considerando que l_c(min)= 3.26 , tenemos la ecuación 32:

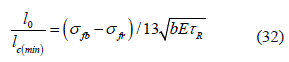
Profundidad de la grieta en la matriz

Para calcular la profundidad de propagación de grietas en la matriz, proponemos llevar a cabo una construcción adicional. Destacamos un elemento cilindrico de matriz, adyacente a una fibra fracturada. Si analizamos este elemento en equilibrio bajo el efecto de los esfuerzos tangenciales, aplicados solamente en la superficie cilíndrica, se establece que la propagación de los esfuerzos de tensión en la matriz sea uniforme, ecuación 33:

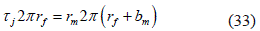
Entonces se puede establecer, que los esfuerzos tangenciales decrecen a medida de que se separan de la fibra fracturada, ecuación 34:τ

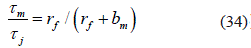
Donde τ_j y τ_m son los esfuerzos tangenciales en el borde de la fibra fracturada y alejada de ella a una profundidad b_m, respectivamente. Si disminuyen los esfuerzos tangenciales, entonces se reduce la intensidad del esfuerzo en la matriz, y se expresa como: 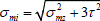. Por lo tanto, si en el borde de la fibra fracturada se cumple el criterio de fractura de la matriz σ_fb>σ_fm, entonces a una cierta distancia de la fibra, este criterio puede no cumplirse.

Se considera que en las regiones vecinas, donde se cumple el criterio de fractura de la matriz, y donde este no se cumple, son los límites de micro grietas que surgen en la matriz durante la fractura de la fibra. Entonces, la profundidad de la grieta en la matriz se determinará de las condiciones expresadas en la ecuación 35:

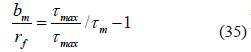
Donde τ_max, es el valor máximo de los esfuerzos tangenciales que surgen en el borde de la fibra fracturada y la matriz, τ_m es el esfuerzo en el borde de la grieta con profundidad b_m que se obtiene de las condiciones σ_fb>σ_fm.

La relación τ_max / τ_m se describirá de diferente forma en función de un mayor o menor esfuerzo de fluencia de la matriz al corte con los valores τ_max y τ_m o bien, en función de un mayor o menor .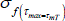

La simulación numérica de semejantes micro mecanismos de fractura, tales como la delaminación de la fibra, y el desarrollo de grietas en la matriz, requiere de la construcción de modelos estructurales tridimensionales de compuestos.

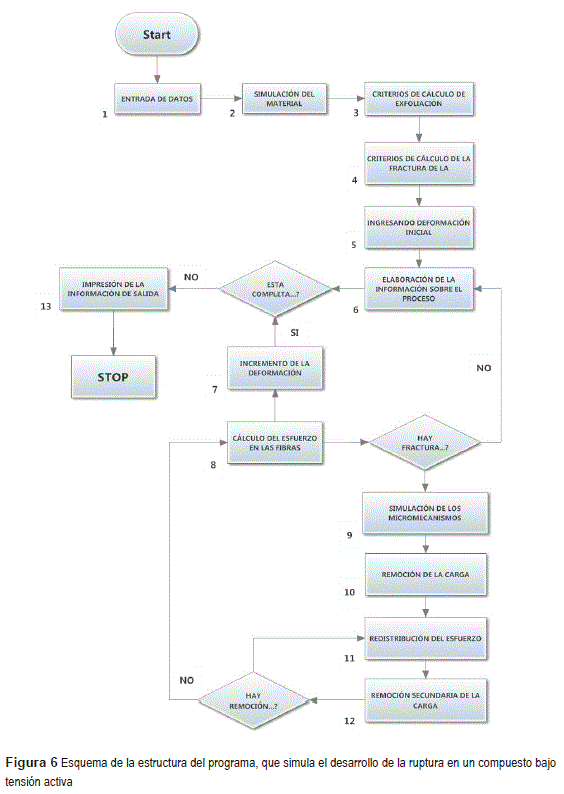
Los eventos individuales de fracturas de las fibras son el micro mecanismo primario de rompimiento del compuesto con fibras frágiles y matriz dúctil. Junto con el rompimiento de las fibras individuales en el modelo que proponemos, simulamos micro mecanismos secundarios de fractura: exfoliación de las fibras fracturadas de la matriz, rompimiento de las fibras por sobrecargas localizadas, y rompimiento de los volúmenes adyacentes de matriz. En base a estas consideraciones desarrollamos un bloque esquemático de la interacción de los diferentes micro mecanismos de fractura y las consecuencias de los efectos de las sobrecargas localizadas y su aporte al trabajo de las fibras durante el desarrollo del proceso de exfoliación, y que es básico para la estructuración del programa y formulación de los algoritmos a través de un programa cuyo diagrama de bloques se muestra en la figure 6.

Conclusiones

Se detectó uno de los mecanismos que obstaculizan la ruptura del compuesto cuando disminuye la fuerza de adherencia entre los componentes del sistema. El estudio de estos efectos permite de la misma forma plantear el problema de cómo optimizar el calibre de la fuerza de adherencia entre los componentes del sistema, que asegura la integridad monolítica del material y la correspondiente redistribución de los esfuerzos, por un lado, y por el otro - garantiza el amortiguamiento de los procesos dinámicos y la requerida ductilidad de fractura del compuesto en su conjunto.

El trabajo con un modelo lineal estructural discreto, corroboró la suposición de que la razón de la fractura de las fibras en trozos significativamente inferiores a la longitud crítica, reside en la sobrecarga que se genera en la fibra fracturada y su propagación longitudinal.

La fragmentación secuencial de las fibras aproximadamente en trozos iguales es el resultado de la interferencia de las ondas de sobrecarga, procedentes de diferentes centros de ruptura. La exfoliación, o separación de la fibra fracturada de la matriz reduce el nivel de sobrecarga, y la probabilidad de posteriores rompimientos de la fibra.

El pronóstico directo de las propiedades del material compuesto requiere del uso de modelos más complejos, en particular, de modelos que permiten reproducir en los computadores las transiciones cualitativas a partir de la etapa de acumulamiento de daño hasta llegar a la macro fractura del material.

El desarrollo ulterior de estos problemas supone el desarrollo de investigaciones en las siguientes direcciones fundamentales:

1. Estudio y sistematización de los mecanismos de fractura de los materiales bajo diferentes niveles estructurales.

2. Caracterización de las propiedades mecánicas de los componentes estructurales, desarrollo de métodos estadísticos para su descripción y métodos de evaluación de las propiedades localizadas de micro volúmenes.

3. Construcción de modelos y algoritmos de redistribución del esfuerzo, relacionados con los diferentes actos de acumulación de daño en el material.

4. Desarrollo de modelos complejos estructurales y de los algoritmos que hacen posible reproducir en los computadores los distintos fenómenos en estudio.

Los resultados obtenidos y los ejemplos analizados por simulación computarizada para la solución de múltiples problemas relacionados con la predicción de las propiedades de resistencia y optimización de la estructura de los materiales compuestos, permiten exponer que es una nueva tendencia en los procesos de investigación de los procesos de fractura de los materiales que se fundamentan en el método de la simulación estructural de complejos sistemas.

Agradecimientos

El presente trabajo fue posible dentro del marco del proyecto SAPPI N°20121012, Instituto Politécnico Nacional, Secretaría de Investigación y Posgrado; y proyecto CONACyT, N° 84309. Al personal del Laboratorio 20, Instituto de Metalurgia BAIKOV, Academia de Ciencias de Rusia; a los alumnos del Programa de posgrado del IPN, M.C. Julio Cerecedo Márquez e Ignacio Bautista Adame, por la realización de los ensayos de simulación y procesamiento de los datos.

Referencias

1. T. Vaughan, C. McCarthy. ''Micromechanical modeling of the transverse damage behavior in the fiber reinforced composites''. Composites Science and Technology. Vol. 71. 2011. pp. 388-396.         [ Links ]

2. B. Rosen. Mechanics ofstrain-hardening ofcomposites, in: Fiber Composites [ Russian translation]. 1^st ed. Ed. Mir. Moscow. Russia. 1967. pp. 54-96.         [ Links ]

3. B. Semionov, S. Kruglov, Y. Tishenkova. ''Study of strength and fracture tensile, reinforced steel and boron fibers''. Composites Materials. 2^nd ed. Ed. M. Nauka. Minsk. Russia. 1981. pp. 82-88.         [ Links ]

4. G. Guniayev, A. Zhigun, B. Perov. ''The strength of born fibers'' The mechanics of polymers. Vol. 6. 1970. pp. 1141-1145.         [ Links ]

5. Y. Gusiev, A. Ovchinsky. ''Modelirovaniye na IBM protsessov razrusheniya voloknistij kompositsionnij materialov pri postoyanno deistvuyushey raztiagivayushey nagruzke'' Mecánica de Materiales Compuestos. Vol. 2. 1984. pp. 263-270.         [ Links ]

6. H. Niederreiter. ''Quasi-Monte Carlo methods and pseudo-random numbers''. Bulletin of the American Mathematical Society. 84^th ed. Boston. USA. 1978. pp. 957-1041.         [ Links ]

7. I. Sobol. Monte Carlo Computational Methods. 1^st ed. Ed. Nauka. Moscow. Russia. 1973, pp. 312.         [ Links ]

8. A.Wilkinson, D. Dingley. ''The distribution of plastic deformation in a metal matrix composite caused by straining transverse to the fibre direction''. Acta Metallurgica et Materialia. Vol. 40. 1992. pp. 3357-3368.         [ Links ]

9. K. Hibbitt. Dassault Systems ABAQUS/Standard User'sManual, version 5.6. Rhode Island, USA. 1996.         [ Links ]

10. E. Car, F. Zalamea, S. Oller, J. Miguel, E. Oñate. ''Numerical simulation of the fiber reinforced composite materials - two procedures''. Int. J. Solids Struct. Vol. 39. 2002. pp. 1967-1986.         [ Links ]

11. E. Barbero, P. Lonetti. ''A damage model for composites defined in terms of available data''. J. mech. Compos. Mater. Struct. Vol. 8. 2001. pp. 299-316.         [ Links ]

12. P. Maimi, P. Camanho, J. Mayugo, C. Davila. ''A continuum damage model for composite laminates: Part I - Constitutive model''. Machanics of Materials. Vol. 39. 2007. pp. 897-908.         [ Links ]

13. S. Mileiko, N. Sorokin, A. Tsirlin. ''Strength of boro-aluminium composite reinforced with brittles fibers''. Mejanika Polimerov. Vol. 5. 1973. pp. 840-846.         [ Links ]

14. C. Davila, P. Camanho, C. Rose. ''Failure criteria for FRP laminates''. J. Compos. Mater. Vol. 39. 2005. pp. 323-345.         [ Links ]

15. R. O'Higgins, C. McCarthy, M. McCarthy.'' Identification of damage and plasticity parameters for continuum damage mechanics modeling of carbon and glass-reinforced composite materials''. Strain. Vol. 47. 2009. pp. 105-115.         [ Links ]

16. D. Trias, J. Costa, J. Mayugo, J. Hurtado. ''Random models versus periodic models for fiber reinforced composites''. Comput. Mater. Sci. Vol. 38. 2006. pp. 316-324.         [ Links ]