Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.70 Medellín Jan./Mar. 2014
ARTÍCULO ORIGINAL
Optimización de secciones de vigas y columnas para el cumplimiento de la deriva en edificaciones de concreto reforzado mediante Redes Neuronales Artificiales
Optimization of beam and column sections for compliance drift of reinforced concrete buildings using Artificial Neural Networks
Jorge Arcila Zea1*, Carlos Alberto Riveros Jerez2, Javier Enrique Rivero Jerez2
1Escuela de Ingeniería. Departamento de Ingeniería Civil. Universidad EAFIT. Medellín. Colombia. AA. 1226.
2Facultad de Ingeniería. Escuela Ambiental. Universidad de Antioquia. Medellín. Colombia. AA.
*Autor de correspondencia: teléfono: + 57 + 4 + 2760032, correo electrónico: jarcila@eafit.edu.co (J. Arcila)
(Recibido el 22 de agosto de 2013. Aceptado el 23 de enero de 2014)
Resumen
Este artículo presenta los resultados del uso de Redes Neuronales Artificiales (RNA) para la estimación de secciones óptimas de vigas y columnas en concreto reforzado en edificaciones aporticadas simétricas de 1 a 6 pisos teniendo en cuenta los requisitos mínimos exigidos en la NSR-10 relacionados con la deriva y el diseño sísmico. Además se estudió la sensibilidad de la deriva respecto a los valores de dimensiones de vigas y de columnas, para que una vez se tenga una mejor comprensión de dicha relación, se puedan obtener diseños óptimos de manera más rápida, sencilla y confiable en comparación con los procedimientos utilizados actualmente.
Palabras clave: Optimización, redes neuronales artificiales (RNA), deriva, diseño sísmico, estructuras aporticadas
Abstract
This article presents the application of Artificial Neural Networks (ANN) to estimate optimal sections of beams and reinforced concrete columns for symmetric framed buildings with 1-6 floors taking into consideration the minimum requirements of the NSR-10 related with drift and seismic design. It is also studied the sensitivity of drift to the values of dimensions of beams and columns providing a better understanding of this relationship in order to obtain optimal designs more quickly, easily and reliably as compared to current used procedures.
Keywords: Optimization, artificial neural networks (ANN), drift, seismic design, framed structures
Introducción
Uno de los objetivos básicos del diseño sísmico es evitar daños en las estructuras ante temblores moderados, restringiendo los desplazamientos laterales en una edificación. La forma más usual de controlar dicho movimiento es limitando la deriva a cierto valor. Para lograr esto, se deben dimensionar las vigas y las columnas (o muros) de tal forma que sean lo bastante rígidos para controlar los desplazamientos de la estructura. Las dimensiones que se plantean para un primer análisis por lo general no son adecuadas y es necesario iniciar un proceso de ensayo y error con secciones hasta encontrar las que permitan cumplir con los requisitos de la deriva en primera instancia. Lo tedioso del proceso anterior hace que se busquen secciones pensando sólo en la seguridad estructural, y poco en la economía, obteniéndose diseños que no son óptimos. Los programas de estructuras actuales, siendo de por sí bastante potentes, no tienen aún incorporadas rutinas para hallar la solución más óptima a un diseño, a pesar de existir técnicas para esto como las Redes Neuronales Artificiales (RNA) y otras más.
En el presente estudio se propone una metodología basada en modelos de RNA para abordar el problema de optimización en estructuras, buscando las secciones de vigas y columnas óptimas que garanticen el cumplimiento de la deriva máxima según lo exigido en las Normas Colombianas de Diseño y Construcción Sismo Resistente (NSR-10), para edificios con pórticos en concreto reforzado. Se estudia además la relación entre secciones de elementos y valores de deriva, para que con un mayor conocimiento de dicha relación se puedan tener diseños correctos y óptimos de una forma más rápida y segura de lo que se hace en el presente.
Inteligencia artificial en la ingeniería estructural
Con el auge de la computación electrónica en los últimos años se ha desarrollado el campo de la inteligencia artificial (I.A), en el cual se busca, a partir de técnicas algorítmicas, emular la capacidad de raciocinio de un ser humano. Las técnicas de I.A más aplicadas en la ingeniería estructural han sido los Algoritmos Genéticos, las Redes Neuronales Artificiales, los Algoritmos de Inteligencia de Enjambre y los Algoritmos de Temple Simulado. Con éstas técnicas se han resuelto una variedad de problemas para los cuales no existe solución analítica o serían bastante dispendiosos de resolver.
Con las técnicas anteriores se han abordado problemas de: diseño de elementos de concreto reforzado [1-6], y de acero [7-11], monitoreo y detección de daño [12], y análisis dinámicos de edificios [13, 14]. Los trabajos reportados e indicados antes se pueden agrupar en dos tipos: problemas de predicción de valores para una o varias variables o de optimización. De éste último tipo es el problema que se considera en la presente investigación.
El problema de la optimización en la ingeniería estructural
Los primeros intentos por optimizar en estructuras se pueden rastrear hasta los trabajos de Maxwell en 1869 y Mitchell en 1904. Sin embargo, fue necesario esperar hasta 1951 para que aparecieran las primeras técnicas para el diseño plástico óptimo de vigas y pórticos [15]. En la década de los 60 se desarrolló el soporte matemático de las teorías de optimización, las cuales comenzarían a ser aplicadas, en el caso de la ingeniería estructural, en los años 70 [16].
RNA en la ingeniería estructural
La técnica que se plantea para el presente estudio son las RNA. Su uso en ingeniería civil no es nuevo, ya que sus primeros usos datan de los años 80 en las áreas de estructuras, recurso hídrico, vías y transporte y geotecnia [17]. Al igual que otras técnicas de I.A, las RNA se han empleado en la ingeniería estructural para estudiar problemas sobre: diseño de elementos en concreto reforzado con acero y fibras [5, 6], detección de daño en estructuras [12], análisis dinámico de estructuras en acero [13] y en concreto [14], análisis no lineal de estructuras de concreto [18, 19], diseño de estructuras basado en desempeño [20], análisis de confiabilidad en estructuras [21], y diseño de elementos en acero [22, 23]. En los problemas antes mencionados es posible identificar dos usos distintos de las RNA: uno enfocado en la predicción de uno o varios valores en un problema como en [6, 12-14, 18, 19] y otro enfocado en la optimización de una o varias variables como en [5, 20-23].
Redes neuronales artificiales: definiciones básicas, características y fases de modelación
Las RNA son una herramienta computacional que pretende emular el proceso de trabajo de las neuronas del cerebro y del sistema nervioso de los seres humanos. Una RNA está constituida por: i) un conjunto de entradas y/o de salidas, ii) los pesos sinápticos, iii) la regla de propagación, iv) la función de activación y v) la función de salida [24]. Una vez seleccionado el tipo y arquitectura de la RNA, se siguen tres etapas con el fin de calibrarla: la etapa de entrenamiento en la cual se ajustan los pesos sinápticos; la etapa de validación en la cual se minimiza el posible sobreajuste y la etapa de prueba en la cual se analiza la capacidad predictiva de la red.
El modelo de RNA que se empleó en esta investigación fue el perceptrón multicapa (MLP en inglés). El MLP es una RNA multicapa empleada como aproximador universal de funciones. Su arquitectura está constituida por una capa de neuronas de entrada, una de salida y una oculta (aunque podría contener n capas ocultas). Se seleccionó este tipo de red por cuatro razones: 1) su capacidad de modelar datos de modelos no lineales, 2) su capacidad de extraer las características más significativas de los datos de entradas, mejorando su capacidad predictiva, 3) su alta conectividad entre neuronas lo cual le permite calcular de mejor forma los pesos sinápticos, y 4) el extenso uso que se ha dado a este tipo de red en investigaciones en diversos campos. De hecho, es el modelo más empleado en las aplicaciones prácticas. [25, 26]. El algoritmo más usado para entrenar un MLP es el de retropropagación o back-propagation (BP). Este se fundamenta en calcular el error en los datos de la capa de salida, y luego propagarlo hacia la capa oculta para modificar los pesos sinápticos de las neuronas de dicha capa. El proceso continúa hasta que se alcance un valor de tolerancia o cierto número de iteraciones. El BP tiene dos desventajas: su lentitud de convergencia y su facilidad de caer sobreajustes. Para resolver estos inconvenientes se han desarrollado métodos para mejorar el BP como: los algoritmos de gradientes conjugados y conjugados escalados y el algoritmo de Levenberg-Marquardt [24, 26]. De los tres mencionados, se usó en esta investigación el algoritmo de Levenberg-Marquardt debido no sólo al buen desempeño que ha tenido en investigaciones similares a ésta sino también porque es reconocida su capacidad de minimizar errores en funciones no lineales [26].
Metodología usada
Se seleccionaron las RNA para el presente problema ya que son una técnica que le permite al diseñador estructural almacenar muchos diseños óptimos y luego entrenar una red neuronal que podría usar para estimar las secciones óptimas de los elementos estructurales en una edificación. Esto le ayudaría al diseñador estructural a ahorrar tiempo y lograr un diseño óptimo. Frente a otras posibles técnicas de optimización, las RNA ofrecen algunas ventajas: i) pueden ser alimentadas en forma constante con más datos para mejorar su capacidad de predicción, ii) captan fácilmente las relaciones entre los datos de entrada y de salida en un problema dado a pesar del posible ruido que puedan tener los mismos, y iii) permiten una implementación sencilla y rápida por parte del diseñador estructural.
Definición de la función objetivo y restricciones
En los problemas de optimización es necesario definir una función objetivo. Una función objetivo es aquella que representa cualquier cantidad que se desee minimizar o maximizar [27, 28]. Dada la complejidad del modelo matemático de la respuesta dinámica tridimensional de una edificación, no fue posible obtener una función analítica de la deriva en términos de las secciones de los elementos estructurales. Sin embargo, se sabe de la dinámica de estructuras que la deriva es función de varias propiedades de una edificación que definen cómo responde ésta a una carga dada. Esto se expresa en la ecuación (1), a manera de función objetivo ''conceptual''. Dicha función es necesario definirla como un conjunto de datos, obtenidos de diversas estructuras modeladas con elementos finitos para las cuales se calculaban las derivas a medida que se cambiaban las dimensiones de sus elementos.
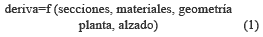
Las restricciones para (1) también se definieron: se dejaron fijos los materiales y las geometrías y se limitó la deriva máxima al 1,0 % de la altura de entrepiso, según se indica en [29].
Definición de la geometría y propiedades mecánicas de los materiales usados en los modelos
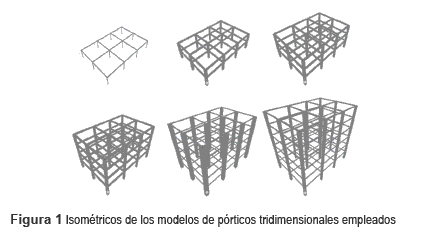
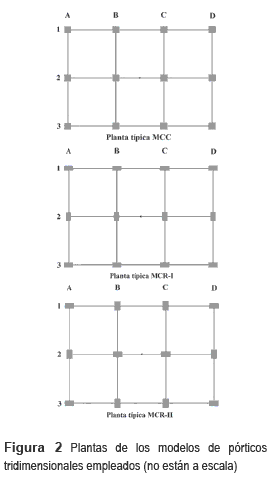
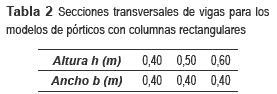
Las estructuras modeladas eran con pórticos 3D regulares en altura y en planta, construidas en concreto reforzado, con luces iguales de 6,0 m, espesor de losa de 0,10 m, altura entre pisos de 3.0 m y número de pisos entre 1 y 6 nombrados como T1, T2, T3, T4, T5 y T6. Se definieron modelos con columnas cuadradas (MCC), y con modelos con columnas rectangulares (MCR). A su vez, de este último hay dos subtipos, diferenciados sólo por la orientación de algunas columnas, llamados MCR-I y MCR-II. Para el análisis de los mismos se empleó el programa SAP2000®. Para los MCC se definieron 20 tamaños de vigas y a cada uno se asignaron 15 secciones de columna desde 0,10 m hasta 0,80 cm de lado. Para los MCR-I y MCR- II se definieron 3 tamaños de vigas y a cada uno se asignaron tamaños de columnas rectangulares con valores de altura de 0,80 m hasta 0,40 m con variaciones de 0,10 m. El ancho se determinó según relaciones anchoCOL/alturaCOL iguales a 0.4, 0.5 y 0.6. La idea de tener tal cantidad de secciones es contar con varios valores que describan correctamente la función objetivo y que además permitan estudiar la sensibilidad de la deriva a cambios en la sección transversal, aunque muchas de éstas no sean aptas desde el punto de vista del diseño sísmico. Es importante aclarar también que hay más secciones de columnas cuadradas que rectangulares por dos motivos: primero, la sección cuadrada es única, ya que una de sus dimensiones es igual a la otra, mientras que en el caso de secciones rectangulares se tienen más posibilidades lo cual necesariamente obliga a seleccionar sólo algunas rectangulares, y segundo, porque la sección cuadrada para una columna es la menos óptima, ya que aporta igual inercia en sus dos direcciones principales. El concreto se definió con peso específico de 24,0 kN/m3, y relación de Poisson 0,20. Para las vigas se tomó una resistencia a la compresión de 21.0 MPa y para las columnas de 28.0 MPa. El módulo de elasticidad se calculó de acuerdo con lo planteado en C.8.5.1 en [29] para concreto de densidad normal. En las figuras 1 y 2 se presentan los isométricos y las plantas de los modelos usados mientras que en las tablas 1 y 2 se presentan las secciones de vigas definidas.
Cargas para el modelo
Para todos los modelos se consideraron dos tipos de cargas: las muertas debidas al peso propio de la estructura y las cargas sísmicas. Las cargas muertas eran calculadas por el programa SAP2000® de forma automática y comprendía el peso de vigas, columnas y losa. El análisis dinámico se llevó a cabo usando el Método Modal Espectral, para el espectro de diseño propuesto en [29] para la ciudad de Medellín (Colombia) con un perfil de tipo C.
Datos y arquitectura para los modelos de RNA
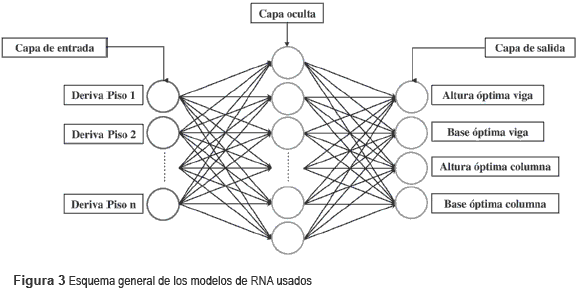
De acuerdo a lo explicado, se obtuvieron 1800 MCC, 270 MCR-I y 270 MCR-II, para un total de 2.340 modelos. Con los datos obtenidos se creó una base de datos donde se relacionaban los valores de derivas con la sección de vigas y columnas correspondiente. Se definieron 6 modelos de RNA tipo MLP para cada modelo de edificio de 1 a 6 pisos. Dichos modelos de RNA se llevaron a cabo en MATLAB® y fueron creadas de acuerdo a lo expresado en (1) y sus restricciones, definiendo como entradas las derivas y como salidas las secciones de vigas y columnas óptimas para el valor de deriva requerido. El número de neuronas en la capa de entrada es igual al número de pisos del modelo correspondiente (es decir, entre 1 y 6), en la de salida es de 4 (altura y ancho de viga y de columna) y en la oculta se definió de acuerdo con las necesidades de convergencia y de entrenamiento que surgían en cada modelo. La función de activación usada fue la sigmoidal, ya que es adecuada cuando se usan datos de modelos no lineales [26]. Los datos usados para cada fase de entrenamiento eran seleccionados en forma aleatoria por MATLAB® pero tomando siempre con porcentajes 70-15-15 de acuerdo con lo sugerido en [30]. El esquema de las RNA usadas se presenta en la figura 3.
Resultados obtenidos para los modelos de RNA
Valores predichos por los modelos de RNA
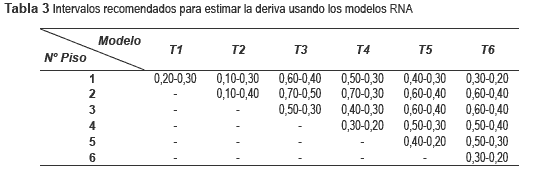
Se decidió determinar qué valores de deriva se podrían recomendar para el uso de los modelos de RNA creadosyllevar acabo estimaciones confiables de la sección óptima. Dichos valores fueron dados en forma de intervalos. Estos intervalos se obtuvieron observando que contuvieran al menos el 75 % de los datos obtenidos para cada piso y tipo de modelo particular. Con el fin de hacer una selección racional de los mismos, se descartaron: i) aquellos modelos con secciones que condujeron a valores mayores para la deriva de acuerdo con lo planteado por A.6.4.1 en [29] y ii) aquellos con secciones menores que las exigidas por C.21.3.4 en [29] para estructuras con capacidad especial de disipación de energía (DES). Los intervalos se presentan en la tabla 3.
Alcances y limitaciones de los modelos de RNA
Los alcances y limitaciones de los modelos RNA y valores propuestos acá se estudiaron a partir de dos puntos clave: i) Sistema estructural: la respuesta sísmica de edificaciones está controlada en buena parte por el sistema estructural usado ya que determina la forma de transmitir las cargas, y controlar los desplazamientos; ii) Geometría en planta y en alzado: la irregularidad geométrica en una estructura determina su capacidad de disipar energía durante un sismo e influye en sus desplazamientos laterales. Éstas hacen menos eficiente un sistema estructural dado. De los dos tipos de irregularidades geométricas posibles, aquellas en planta son las que más afectan la deriva, ya que hacen que no coincidan los centros de rigidez y de masa en un nivel ocasionando momentos torsores que deben tenerse en cuenta en el cálculo de la deriva. Teniendo en cuenta lo antes expuesto, sólo se recomienda el uso de los modelos RNA y los valores acá sugeridos a sistemas estructurales en pórticos con un número de pisos entre 1 y 6 y regulares en planta.
Resultados sobre la influencia de las columnas y las vigas en la deriva
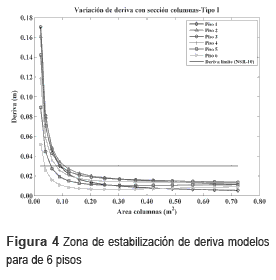
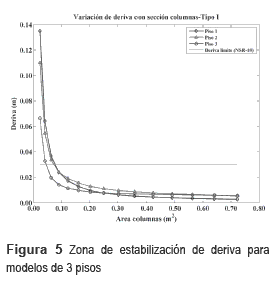
Se pudo determinar que la deriva se estabiliza para todos los pisos de una edificación con pórticos y regular a partir de un valor determinado de sección de columnas. Este valor da inicio a lo que acá se denominará como zona de estabilización de deriva la cual corresponde a aquella porción de las curvas deriva contra área de columnas cuadradas en la cual la gráfica tiene una tendencia lineal. Lo anterior implica que aunque haya un incremento en la sección de las columnas no mejora la deriva. Estas curvas tiene dos características importantes: i) no cambian su tendencia conforme cambia la sección de vigas manteniendo el mismo comportamiento en todos los casos y ii) fueron definidas para secciones cuadradas, ya que son las menos óptimas al tener igual inercia en ambos sentidos. Para cada tipo de edificación según su número de pisos y para cada sección de vigas, se construyó la respectiva curva basados en los MCC. En todas ellas se pudo constatar la tendencia ya mencionada. Además se notó que esta zona iniciaba aproximadamente en el mismo punto para modelos con igual número de pisos, independiente de la sección de viga usada. Teniendo en cuenta lo anterior, se pudo seleccionar para cada tipo de modelo el valor de sección de columna óptimo, el cual corresponde al valor de sección más cercano al punto donde inicia la zona de estabilización en cada caso. Respecto a la orientación de las columnas, se obtuvieron mejores resultados para la deriva en MCR-I y MCR-II. Para dos columnas con igual área, se obtuvieron derivas menores para aquellas con geometría rectangular. Es importante anotar que la sección rectangular es la más óptima, ya que permite definir un lado fuerte y uno débil los cuales se orientan según las necesidades de rigidez lateral en la edificación.
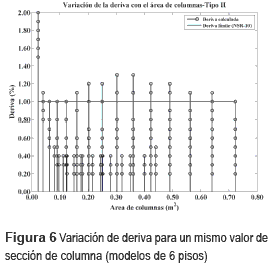
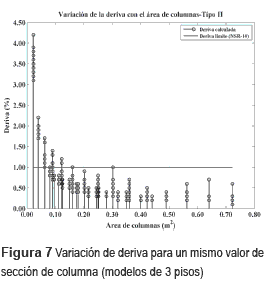
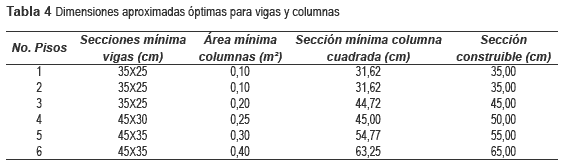
Respecto a las vigas, se pudo constatar que para una misma sección de columna se obtienen diferentes valores de deriva según la sección de viga considerada, lo cual demuestra una influencia de las vigas en las derivas. Esta influencia, determinada por las diferencias entre los valores de deriva para una misma sección de columna es más notoria en los pisos superiores que en los inferiores. De nuevo esta tendencia se pudo corroborar con todas las secciones de viga usadas. Puede decirse entonces que las vigas, además de rigidizar la losa (aumentando el efecto de diafragma rígido en su plano), ayudan al control de derivas principalmente en los pisos del tercio superior de la edificación. Esto está en concordancia con el comportamiento esperado para el sistema estructural en pórticos, el cual es menos eficiente para el control de derivas en los pisos superiores. Para aclarar lo antes explicado, se definieron dos tipos de gráficas de variación de deriva contra sección de columna cuadrada: la tipo I definida para una misma sección de viga y utilizada para mostrar en forma principal la estabilización de las derivas con el aumento de la sección de columnas y la tipo II definida para todas las secciones de viga usadas y utilizada para mostrar en forma principal cómo cambia la deriva con la sección de viga. Por razones de espacio sólo se presentan dos ejemplos de cada una de las gráficas mencionadas. En las figuras 4 y 5 se muestran gráficas tipo I y en las figuras 6 y 7 gráficas tipo II. De acuerdo con lo hallado hasta acá, y de acuerdo con C.9.5.2 en [29] para el control de deflexiones, y con C.21.3.4 en [29] para evitar el mecanismo de falla viga fuerte-columna débil, se obtuvieron las secciones mínimas de vigas y columnas a partir de las cuales se cumplen los requisitos de diseño sísmico, y que además por ser las mínimas adecuadas, representan el menor costo. Estas secciones pueden tomarse como referencia para iniciar el predimensionamiento de estructuras de aporticadas y regulares como las estudiadas acá. Dichas dimensiones se presentan en la tabla 4.
Resumen y conclusiones
Se planteó una aplicación de RNA a la obtención de secciones óptimas de vigas y columnas en edificaciones aporticadas y regulares de 1 a 6 pisos en concreto reforzado. Luego de elaborar varios modelos en SAP2000® con diversas secciones de elementos, se calcularon las derivas en dichos modelos. Con estos datos de secciones y derivas se crearon modelos RNA en MATLAB® que permitieran estimar la sección óptima en cualquier otra edificación con características similares de sistema estructural, geometría y número de pisos a las consideradas en este estudio. Se definieron intervalos para valores de deriva los cuales pueden usarse como base para estimar las secciones en elementos por medio de los modelos RNA, teniendo en cuenta la deriva esperada por el diseñador según su criterio. Se determinó la existencia de una zona de estabilización de deriva para estructuras aporticadas y simétricas. Esta zona se caracteriza porque al aumentar la sección de columnas no se reducen los valores de deriva. El punto donde esta tendencia lineal inicia corresponde a la sección óptima para el tipo de edificación considerada. Respecto a las vigas se determinó que para una misma sección de columnas se obtienen diferentes valores de deriva según la sección de viga que se emplee. Las diferencias entre valores de deriva son más marcadas en los pisos superiores donde los pórticos son menos eficientes para el control de desplazamientos laterales. Además, para mayores secciones de vigas se controlan mejor las derivas, ya que ayudan a rigidizar el diafragma. Teniendo en cuenta lo planteado, se determinaron las secciones óptimas para los modelos creados. Estos valores pueden usarse como referencia para estimar secciones en edificaciones con características similares a las acá estudiadas. Dichos valores se presentan en la tabla 4. La metodología acá propuesta podría extenderse a otros sistemas estructurales, con algunos tipos de irregularidades y diferente número de pisos.
Agradecimientos
Este artículo forma parte de los resultados del proyecto de investigación titulado ''Desarrollo de algoritmos de optimización de diseño de estructuras de concreto reforzado'' registrado con el código PI10-1-07 en la Sede de Investigación Universitaria de la Universidad de Antioquia, ejecutado por los autores en 2011. Los recursos fueron proporcionados por la Escuela Ambiental, adscrita a la Facultad de Ingeniería de la misma Universidad
Referencias
1. N. Lagaros, M. Papadrakakis, G. Kokossalakis. ''Structural optimization using evolutionary algorithms''. Computers and Structures. Vol. 80. 2002. pp. 571-589. [ Links ]
2. C. Camp S. Pezeshk, H. Hansson. ''Flexural design of reinforced concrete frames using a genetic algorithm''. Journal of Structural Engineering. Vol. 129. 2003. pp. 105-115. [ Links ]
3. N. Ahmadi, R. Moghadas, A. Lavaei. ''Dynamic analysis of structures using neural networks''. American Journal of Applied Sciences. Vol. 5. 2008. pp. 1251-1256. [ Links ]
4. M. Sonmez. ''Discrete optimum design of truss structures using artificial bee colony algorithm''. Structural and Multidisciplinary Optimization. Vol. 43. 2011. pp. 85-97. [ Links ]
5. D. Suji, S. Natesan, R. Murugesan, R. Sanjai. ''Optimal design of fibrous concrete beams through simulated annealing''. Asian Journal of Civil Engineering-Building and Housing. Vol. 9. 2008. pp. 193-213 [ Links ]
6. C. Ferreira, M. Barros, A. Barros. ''Optimal design of reinforced concrete T-sections in bending''. Engineering Structures. Vol. 25. 2003. pp. 951-964. [ Links ]
7. M. Leps, M. Sejnoha. ''New approach to optimization of reinforced concrete beams''. Computers and Structures. Vol. 81. 2003. pp. 1957-1966. [ Links ]
8. C. Coello, A. Christiansen. ''Multiobjective optimization of trusses using genetic algorithms''. Computers and Structures. Vol. 75. 2000. pp. 647-660. [ Links ]
9. M. Ghozi, P. Aji, P. Suprobo. ''Evolutionary Parallel SAP2000 for truss structure optimization''. International Journal Academic Research. Vol. 3. 2011. pp. 1140-1145. [ Links ]
10. C. Chan, M. Wong. ''Evolutionary optimization of braced steel frameworks for tall buildings using a hybrid OC-GA method''. Advances in Engineering Structures, Mechanics and Construction-Solid Mechanics and Its Applications. Vol. 140. 2006. pp. 205-214. [ Links ]
11. J. Lee. C. Yun. ''Damage localization for bridges using probabilistic neural networks''. KSCE Journal of Civil Engineering. Vol. 11. 2007. pp. 111-120. [ Links ]
12. N. Caglar, M. Elmasa, Z. Yamana, M. Saribiyikb. ''Neural networks in 3-dimensional dynamic analysis of reinforced concrete buildings''. Construction and Building Materials. Vol. 22. 2008. pp. 788-800. [ Links ]
13. G. Vanderplaats. ''Structural optimization: where we've been and where we're going''. Computer Aided Optimum Design of Structures V. Vol. 28. 1977. pp. 45-54. [ Links ]
14. L. Schmit, B. Farshi. ''Some approximation concepts for structural synthesis''. Journal of American Institute of Aeronautics and Astronautics. Vol. 12. 1974. pp. 692-699. [ Links ]
15. H. Adeli. ''Neural Networks in Civil Engineering: 1989-2000''. Computer-Aided Civil and Infrastructure Engineering. Vol. 16. 2001. pp. 126-142. [ Links ]
16. M. Hadi. ''Neural networks applications in concrete structures''. Computers and Structures. Vol. 81. 2003. pp. 373-381. [ Links ]
17. N. Caglar. ''Neural network based approach for determining the shear strength of circular reinforced concrete columns''. Construction and Building Materials. Vol. 23. 2009. pp. 3225-3232. [ Links ]
18. M. Hakan. ''An evaluation of effective design parameters on earthquake performance of RC buildings using neural networks''. Engineering Structures. Vol. 32. 2010. pp. 1888-1898. [ Links ]
19. O. Möller, R. Foschi, L. Quiroz, M. Rubinstein. ''Structural optimization for performance-based design in earthquake engineering: Applications of neural networks''. Structural Safety. Vol. 31. 2009. pp. 409-499. [ Links ]
20. N. Lagaros, M. Papadrakakis. ''Neural network based prediction schemes of the non-linear seismic response of 3D buildings''. Advances in Engineering Software. Vol. 44. 2012. pp. 92-115. [ Links ]
21. N. Lagaros, M. Papadrakakis. ''Reliability-based structural optimization using neural networks and Monte Carlo simulation''. Computer Methods in Applied Mechanics and Engineering. Vol. 191. 2002. pp. 3491-3507. [ Links ]
22. L. Zhang, G. Subbarayan. ''An evaluation of back- propagation neural networks for the optimal design of structural systems: Part I. Training procedures''. Computer Methods in Applied Mechanics and Engineering. Vol. 191. 2002. pp. 2873-2886. [ Links ]
23. L. Zhang, G. Subbarayan. ''An evaluation of back- propagation neural networks for the optimal design of structural systems: Part II. Numerical evaluation''. Computer Methods in Applied Mechanics and Engineering. Vol. 191. 2002. pp. 2887-2904. [ Links ]
24. E. Caicedo, J. López. ''Perceptrón Multicapa y Algoritmo Backpropagation''. Una aproximación práctica a las Redes Neuronales Artificiales. 1a ed. Ed. Universidad del Valle. Cali, Colombia. 2009. pp. 75-136. [ Links ]
25. B. del Brío, A. Sanz. ''Fundamentos de las Redes Neuronales Artificiales'', ''Redes Neuronales Supervisadas'', ''Aplicaciones de Redes Neuronales Artificiales''. Redes neuronales y sistemas difusos. 2a ed. Ed. Alfaomega. Ciudad de México, México. 2002. pp. 13-32, pp. 63-84, 209-240. [ Links ]
26. S. Haykin. ''Introduction'', ''Learning Processes'', ''Single Layer Perceptrons'', ''Multilayer Perceptrons''. Neural Networks. A comprehesive foundation. 2a ed. Ed. Pearson Prentice Hall. Singapur, Singapur. 1999. pp. 23-71, 72-124, 136-170, 178-266. [ Links ]
27. B. Gottfried, J. Weisman. ''Introduction'', ''Optimization fundamentals''. Introduction to optimization theory. 1st ed. Ed. Prentice Hall. New Jersey, USA. 1973. pp. 4-22, 26-57. [ Links ]
28. R. Haftka, Z. Gürdal. ''Classical tools in Structural Optimization''. Elements of Structural Optimization. 3rd ed. Ed. Kluwer Academic Publishers. Amsterdam, The Netherlands. 1992. pp. 23-61. [ Links ]
29. AIS. ''Título A'', ''Título C''. Normas Colombianas de Diseño y Construcción Sismo-Resistente. Bogotá, Colombia. 2010. pp. A15-A30, A76, C42, C69, C178. [ Links ]
30. M. Hudson, M. Hagan, H. Demuth. ''Multilayer Networks and Backpropagation Training''. Neural Network Toolbox, User's Guide. Ed. The Mathworks Inc. Natick, USA. 2011. pp. 3.2-3.28. [ Links ]