Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.70 Medellín jan./mar. 2014
ARTÍCULO ORIGINAL
Método basado en clasificadores k-NN parametrizados con algoritmos genéticos y la estimación de la reactancia para localización de fallas en sistemas de distribución.
OA fault location method applied in power distribution systems based on k-NN classifiers parameterized using genetic algorithms and the reactance estimation
Andrés Zapata-Tapasco, Sandra Pérez-Londoño, Juan Mora-Flórez*
Grupo de Investigación en Calidad de Energía Eléctrica y Estabilidad (ICE3), Universidad Tecnológica de Pereira. CP 660003. Pereira, Colombia.
*Autor de correspondencia: telefax: + 57 + 6 + 321 1757, correo electrónico: jjmora@utp.edu.co (J. Flórez)
(Recibido el 6 de febrero de 2012. Aceptado el 09 de octubre de 2013)
Resumen
En este artículo se presenta una estrategia de parametrización de un localizador de fallas basado en una técnica simple pero eficiente de aprendizaje, conocida como k vecinos más cercanos (k-NN). Esta técnica se complementa con un método plenamente probado de localización basado en la estimación de la impedancia de falla.
La estrategia híbrida se validó en un circuito prototipo real, con resultados de error aceptables para aplicaciones en sistemas de distribución de energía eléctrica. Finalmente y como ventaja importante de la metodología propuesta se resalta la facilidad de implementación, cuando se trata de circuitos de distribución reales (más de 100 nodos).
Palabras clave: Híbrido, impedancia de falla, localización de fallas, k vecinos más cercanos, sistemas de distribución
Abstract
In this paper, a parameterization strategy of a k nearest neighbors (k-NN) based fault locator is described. This technique is complemented by a well validated location method based on the estimation of the fault impedance.
This hybrid strategy is validated in a real power distribution feeder, having obtained acceptable results. Finally and as an important advantage of the here proponed methodology, it is remarkable the easy implementation process, considering real distribution feeders (more than 100 nodes).
Keywords: Hybrid, fault impedance, fault location, k nearest neighbors, power distribution systems
Introducción
Un tema de actualidad e importancia en el sector eléctrico mundial es la calidad de la energía, ya que los nuevos esquemas de regulación demandan que las empresas presten un mejor servicio. Así mismo, una de las principales causas de la pérdida de continuidad en los sistemas eléctricos son las fallas paralelas, que según diferentes estudios, cerca al 80% ocurren en el sistema de distribución [1]. El restablecimiento depende del tiempo de la localización de la falla, que en la mayoría de empresas distribuidoras, debido a problemas de infraestructura, está asociado a una posible llamada telefónica de usuarios afectados o al tiempo que demora la cuadrilla en localizar la falla mediante una inspección visual de la sección de red que se presume afectada [2].
Los métodos basados en el modelo eléctrico de la red, proporcionan información sobre la distancia asociada a la impedancia de falla, desde la subestación hasta el lugar donde ha ocurrido la falla [3-6]. Debido al gran número de laterales, la distancia estimada se cumple para varios sitios del sistema, convirtiendo éste en un problema de múltiple estimación, que complica la ubicación del lateral bajo la condición de falla. Existen adicionalmente, modelos basados en la extracción de información de bases de fallas, los cuales han sido probados con éxito en la localización de fallas [7-9].
En este artículo y como alternativa novedosa de solución al problema de localización de fallas en sistemas de distribución, se propone una metodología híbrida que utiliza el análisis de las curvas de reactancia y una técnica de clasificación basada en la estrategia de los k vecinos más cercanos, parametrizada con algoritmos genéticos. Esta última técnica utiliza diferentes características o descriptores extraídos de las señales de tensión y de corriente medidas en la subestación de distribución.
Aspectos teóricos básicos
La técnica de clasificación para localización de fallas a utilizar hace parte de los denominados métodos de aprendizaje basado en ejemplos (MBC), a partir de los cuales se deriva el método basado en el vecino más cercano. Los parámetros de ajuste se hallan utilizando el Algoritmo Genético de Chu Beasley (AGCB). Adicionalmente, un método basado en la estimación de la reactancia de falla (MBM), se utiliza como complemento para estimar la distancia.
En esta sección se presentan los aspectos teóricos más relevantes de estas técnicas.
Técnica de clasificación basada en el método de los k vecinos más cercanos
El método de clasificación basado en los k-vecinos más cercanos (k-NN o k-nearest neighbors) se fundamenta en que las propiedades de un dato x de entrada son similares a las de los datos de su vecindad, entonces éste pertenece a la misma clase que la clase más frecuente de sus k vecinos más cercanos [10]. Esta regla es adecuada para abordar un problema de aprendizaje, debido a sus propiedades estadísticas bien establecidas y la sencillez de implementación en problemas reales.
El algoritmo general del método de los k vecinos más cercanos asume que todos los ejemplos corresponden a puntos en un espacio p-dimensional 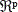 los cuales tienen establecida una clase C. Los datos de entrenamiento son de la forma presentada en (1).
los cuales tienen establecida una clase C. Los datos de entrenamiento son de la forma presentada en (1).
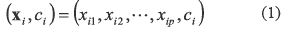
Para un nuevo punto xq se calcula la distancia a los ejemplos de entrenamiento de acuerdo a la función de distancia escogida. Se seleccionan aquellos más cercanos y se asigna al nuevo dato una clase dependiendo del método de asignación.
En caso que se presente un empate entre dos o más clases, se debe contar con alguna regla heurística para su ruptura. Algunas de estas reglas consisten en seleccionar la clase a la cual pertenece el vecino más cercano o seleccionar la clase con distancia media menor [10].
Algoritmo Genético de Chu Beasley(AGCB)
Este algoritmo fue diseñado principalmente para resolver el problema de la designación generalizada, y en este caso aplicado en la parametrización del clasificador k-NN.
El AGCB presenta varias modificaciones con respecto a la teoría fundamental de los algoritmos genéticos cuyas características más importantes son [11]: a) Utiliza la función objetivo para identificar los individuos de mejor calidad y permite manejar infactibilidad; b) Reemplaza sólo un individuo de la población en cada ciclo generacional, sólo si el individuo nuevo es de mejor calidad y c) Contiene el criterio de diversidad de los individuos para evitar la convergencia prematura a óptimos locales.
Validación cruzada
El proceso de validación cruzada consiste en dividir el conjunto de entrenamiento en n subconjuntos. El MBC se entrena con (n-1) subconjuntos y el subconjunto que no se utilizó en el entrenamiento se utiliza para la prueba [3]. Este proceso se repite hasta que cada uno de los n subconjuntos haya sido utilizado en la prueba. El error de validación cruzada se evalúa como una función de los errores en las n pruebas. Este resultado indica el comportamiento global del MBC.
Técnicas de reducción del conjunto de entrenamiento
En la medida que el conjunto de datos que se utiliza para el entrenamiento es más grande, se supone que contiene más información asociada, pero el proceso computacional se hace más lento y exigente. Si se reduce el tamaño de la base de datos de una forma adecuada, es posible conservar la información contenida, reduciendo la exigencia computacional.
Para reducir el tamaño del conjunto de entrenamiento, existen técnicas de condensación y de edición. La técnica de condensación de Hart permite seleccionar un subconjunto de la muestra inicial, de tal forma que los datos faltantes son clasificados correctamente al utilizar el método k NN [12]. La técnica de condensación consiste en seleccionar un conjunto inicial de datos y con éstos se entrena un clasificador k NN inicial. Posteriormente, se clasifican los demás datos; si la clase del nuevo dato es diferente a la previamente asignada, éste entra a ser parte del conjunto de entrenamiento. En el otro caso, si el nuevo dato es clasificado correctamente, éste no se incluye en el conjunto de entrenamiento dado que ya está representado.
Método basado en el gráfico de reactancias
El método a utilizar para la estimación de la distancia de falla es el basado en el principio de la reactancia de falla propuesto por Morales, Mora y Vargas [13]. La descripción detallada de este método está fuera del alcance de está documento.
Metodología propuesta para el desarrollo del localizador basado en k-NN
Como alternativa de solución al problema de localización de fallas que además permite eliminar el problema de múltiple estimación, se propone una metodología híbrida, la cual utiliza un MBM para estimar la distancia a la cual ocurrió la falla y un MBC para encontrar la zona bajo falla.
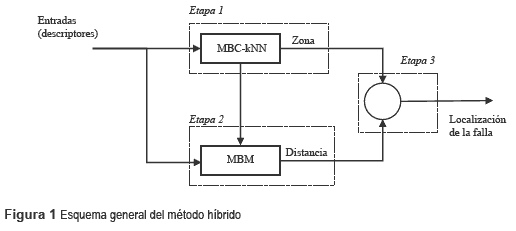
La metodología se basa en una estrategia general utilizada por el método híbrido propuesto para la localización de fallas, tal como se presenta en el esquema mostrado en la figura 1.
En la etapa 1 se implementa el método de clasificación para encontrar la zona en falla. En la etapa 2 y con la zona hallada en la etapa 1, se selecciona un ramal equivalente donde se estima la distancia a la cual ocurrió la falla. Con la distancia y la zona, en la etapa 3 se obtiene la localización de la falla en el sistema de distribución mediante un análisis de las respuestas del MBM y el MBC, eliminando el problema de la múltiple estimación del nodo bajo falla.
Etapa 1: Metodología propuesta para el desarrollo del localizador basado en k-NN
Para la implementación de la máquina de clasificación se siguió un esquema de tres fases, como se presenta en la figura 2. Las entradas o descriptores se definen como las variaciones los valores eficaces de la tensión, la corriente, la potencia aparente y la reactancia, entre las situaciones de prefalla y falla, considerando valores de fase y de línea [3].
Fase 1: Parametrización
Esta es la fase de mayor requerimiento computacional y está orientada a la selección de los mejores parámetros para configurar el clasificador basado en los k vecinos más cercanos (MBC-k NN). En esta fase se utiliza el AGCB como herramienta para seleccionar los mejores parámetros; la técnica de validación cruzada para evaluar los errores de clasificación del MBC- kNN; y también la técnica de condensación de Hart para reducir el conjunto de entrenamiento y así disminuir el tiempo computacional requerido.
La fase de parametrización sigue varios pasos las cuales se mencionan a continuación:
Paso 1: Zonificación de la red de distribución
El proceso de clasificación requiere que para cada uno de los datos de entrenamiento se le asigne una clase, con la cual se realizará la clasificación de un nuevo dato. Como recomendación, se debe tener en cuenta que una zona no debe tener más de un lateral con las mismas fases, para eliminar el problema de múltiple estimación [7].
Paso 2: Adquisición y pre-procesamiento de los datos
Los datos utilizados para el proceso de entrenamiento fueron obtenidos a partir de una herramienta de simulación de circuitos eléctricos utilizando ATP y Matlab [14].
El pre-procesamiento de los datos comprende la asignación de una etiqueta a los datos, dependiendo de la zona en la cual se encuentren, así como la normalización de los mismos para evitar que datos con magnitudes más altas dominen en el cálculo de la distancia.
Paso 3: Definición de los parámetros del MBC-kNN
Los parámetros básicamente representan la forma de calcular la distancia (d), el parámetro de la asignación de la clase (P) y el número de vecinos más cercanos (k). Las normas utilizadas para el cálculo de la distancia (parámetro d), se presentan en las ecuaciones (2) a (5) [15]

La distancia de Mahalanobis se puede expresar como la norma de la ecuación (4), con la matriz W calculada como la matriz de covarianza del conjunto de datos.
Adicionalmente, en el algoritmo básico de clasificación se modifica la manera como se asigna la clase a un nuevo individuo (parámetro P), así: a) k NN con distancia media, donde el nuevo dato se asigna a la clase con menor distancia media; b) k NN con una ponderación que varía inversamente con el cuadrado de la distancia, para que los puntos más cercanos tengan mayor peso y así asignar a la clase para la cual los pesos de sus k casos sumen el mayor valor [16]; c) k NN con distancia mínima, donde se selecciona un sólo caso por clase, normalmente el caso más cercano al baricentro de todos sus puntos. El nuevo dato se asigna a la clase cuyo representante esté más cercano; d) k NN con ponderación de las variables en el cálculo de la distancia.
Finalmente, el parámetro k toma valores enteros y define con cuantos elementos se va a comparar el nuevo dato.
Paso 4: Búsqueda de parámetros óptimos para cada combinación de descriptores
Para cada combinación de descriptores se determinan los parámetros óptimos usando el AGCB.
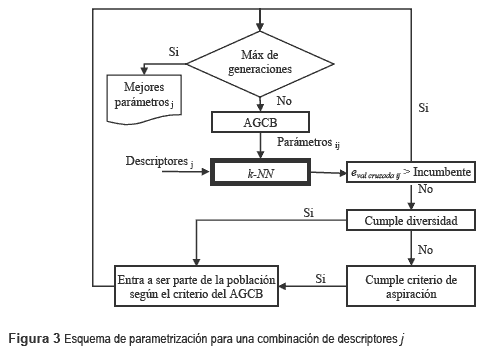
La fase de parametrización para una combinación de descriptores se muestra en la figura 3.
A partir de la figura 3, el AGCB crea una población inicial de individuos que contienen combinaciones deparámetros.Posteriormente, se crean nuevos individuos a partir de la población inicial y se evalúa su función objetivo como el error de validación cruzada (eval cruzada ij) en el método de clasificación. Si este error es mayor a la incumbente, el individuo es poco atractivo para el método y es desechado. En cambio, si es menor, se verifica que cumpla la diversidad para formar parte de la población según el criterio del AGCB. Si el individuo no es diverso, se verifica el criterio de aspiración para que éste forme parte de la población. El AGCB termina cuando se alcanza un número máximo de generaciones (iteraciones) o cuando se obtiene una función objetivo satisfactoria de la población.
Fase 2: Entrenamiento
En k NN no hay entrenamiento propiamente dicho, ya que simplemente lo que se realiza es la selección de la mejor base de datos utilizando la técnica de condensación de Hart. A partir de esta base de datos se realiza la clasificación de los datos de prueba.
Fase 3: Prueba
Con los datos no usados para las fases de parametrización y entrenamiento, se calcula la precisión de la máquina de clasificación. En este paso se obtiene la precisión utilizando los datos de prueba por medio de la ecuación (6), y con la MBC-kNN previamente ajustada con los parámetros óptimos obtenidos para cada una de las combinaciones de datos de entrada, según la fase 1.

Finalmente, utilizando la matriz de confusión de la máquina de clasificación, la cual muestra en las filas la información de cuantos datos fueron clasificados en cada clase y en las columnas cuantos datos pertenecen realmente a esa clase, se puede establecer un índice de confianza del método de clasificación y también identificar las zonas de mayor error.
Etapa 2: Estimación de la distancia al nodo en falla
La metodología propuesta para localización de fallas se basa en el método del gráfico de reactancias presentado por Morales, Mora y Vargas [13]. Como no es posible conocer el valor de cada carga del sistema de distribución, el método concentra la carga total al final del circuito. Para la aplicación propuesta en este artículo, la determinación del tipo de falla se realiza utilizando la propuesta de Ratan Das [4]. Dependiendo del tipo de falla, se selecciona la curva de reactancia de falla adecuada para determinar su localización.
El método de estimación de la distancia de falla, cuando ya se conoce o se ha especificado un sistema radial del circuito según la zona identificada en la etapa 1, se implementa tal como se presenta en [13].
Etapa 3: Unión del MBM y MBC
La etapa de unión se refiere a la localización de la falla a partir de los resultados obtenidos en las dos etapas anteriores. Para la implementación del MBM y MBC es necesario conocer el tipo de falla, que se obtiene utilizando el algoritmo presentado por Ratan Das [4].
En la etapa 1, el MBC distingue la zona en la cual ocurrió la falla, con esta información en la etapa 2 el MBM selecciona el sistema radial y estima la distancia de falla. La unión de esta información proporciona la localización real de la falla.
Aplicación de la metodología propuesta en un sistema de distribución
Esta metodología se desarrolló con ayuda del software Matlab® para elaborar los algoritmos necesarios, el software de simulación de circuitos eléctricos ATP y el software simulaciónRF, propio del equipo de trabajo [14], el cual simula automáticamente unas condiciones de falla deseadas y permite una rápida obtención de las bases de datos necesarias.
Descripción del sistema de prueba y escenarios
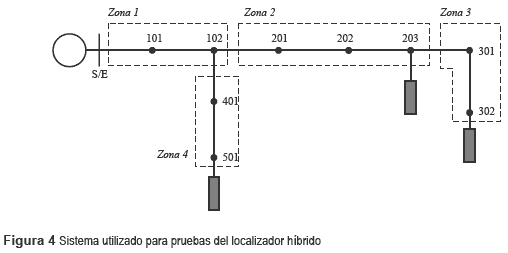
El sistema de prueba es un circuito real de 28 kV que consta de 11 nodos y 10 líneas, con un lateral y tres cargas. En la figura 4 se muestra el sistema de pruebas.
Los escenarios utilizados para probar el algoritmo, incluyen fallas en todos los nodos del sistema excepto en la subestación. Las resistencias de falla corresponden a valores entre 0,5 Ω y 40 Ω en pasos de 5 Ω, los cuales son valores comúnmente usados en este tipo de prueba [17]. Se utilizaron cinco valores de carga diferentes, a 60%, 80%, 100%, 120% y 140% de la carga promedio. En total se utilizaron 4050 registros de falla.
Descripción de la prueba
Los descriptores de entrada al MBC son las variaciones en la tensión, la corriente, la potencia aparente y la reactancia vista desde la subestación (dV, dI, dS y dX). Para cada uno de los descriptores mencionados se tienen las medidas de fase y de línea.
Para la prueba se utiliza una población inicial en el AGCB de 10 individuos y validación cruzada con 5 subconjuntos. Para la población inicial, se tomaron k vecinos más cercanos, correspondientes a fallas localizadas a intervalos de distancia iguales, para garantizar diversidad.
Rango de variación de los parámetros
Los parámetros que definen el clasificador basado en k-NN son tres; d representa la forma de calcular la distancia, P indica la forma de ponderación de los datos y asignación de la nueva clase y k indica el número de vecinos más cercanos utilizados para definir la clase del nuevo individuo.
El parámetro d puede tomar los siguientes valores: 1 para la distancia Euclídea, 2 para la distancia Manhattan, 3 para la norma L∞ o Chebyshev y 4 para la distancia de Mahalanobis.
El valor de P considera los tipos de asignación definidos a continuación: 1 para la selección de la clase con mayor frecuencia, 2 para la selección de la clase con menor distancia media, 3 para la selección de la clase con ponderación de casos seleccionados (1/d), 4 para la selección de la clase con menor distancia a un parámetro representativo, 5 para la selección con ponderación de datos (1/d2) y 6 para la selección con ponderación de datos (e-d).
Los valores de k son enteros y para esta investigación varían desde uno al 40% del número de datos del conjunto de parametrización. Este criterio responde a que se realiza una validación cruzada con 5 subconjuntos, con lo cual el parámetro k está limitado a 80% del total.
Parametrización, entrenamiento y pruebas del algoritmo de clasificación
En esta etapa se deben determinar aquellos parámetros que presenten robustez para diferentes condiciones de carga, así como la selección de la combinación de descriptores que permita una clasificación confiable. En total se realizaron 4 pruebas diferentes, cuyo resultado contiene las combinaciones de descriptores con mejores resultados en la precisión, los parámetros de calibración y el error de validación cruzada (error VC) de la etapa de parametrización.
Caso 1. Parametrización con datos en condiciones promedio
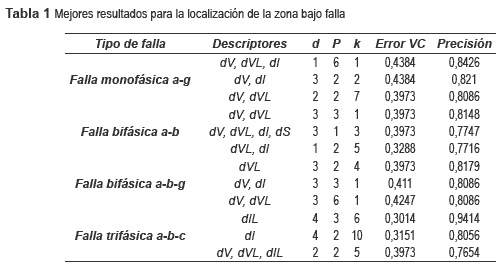
El conjunto de parametrización se obtiene a 100% de la carga promedio con un total 81 datos por cada tipo de falla. Los datos de prueba se obtienen al 60%, 80%, 120% y 140% de la carga promedio y corresponden a 324 registros de falla. Las tres mejores combinaciones de descriptores de entrada se presentan en la tabla 1 para 4 diferentes tipos de fallas.
Para este caso, el mejor desempeño se encuentra alrededor del 80% ante falla monofásica, bifásica o bifásica a tierra. Lo anterior indica que de cada 100 fallas evaluadas, a 80 de ellas se les determina adecuadamente su zona de ocurrencia. Finalmente, se observa un mejor comportamiento en el caso de la falla trifásica donde el desempeño supera el 94%.
Caso 2. Parametrización con los datos de casos extremos de carga
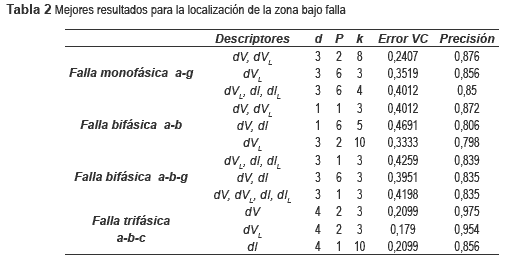
En este caso se utilizaron como datos de parame-trización, los obtenidos a 60% y 140% de la carga promedio. Los datos de prueba son los obtenidos a 80%, 100 % y 120% de la carga promedio. El número de registros de falla de parametrización es de 162 y para pruebas es de 243. Los mejores tres resultados se muestran en la tabla 2.
Se aprecia un incremento en la precisión del localizador de fallas, mostrando así que existe una mejor capacidad para interpolar o inferir un resultado adecuado, a partir de los datos de condiciones extremas. La precisión, comparada con el caso anterior, sube en promedio un 5,2%.
Caso 3. Parametrización inicial con datos en condiciones promedio y adición de datos utilizando condensación de Hart
En esta prueba, utilizando los parámetros obtenidos en el caso 1, se seleccionaron nuevos datos para el conjunto de entrenamiento al 60 y 140% de la carga promedio, a partir de la técnica de condensación de Hart. La precisión se calcula con los datos que no fueron utilizados en el entrenamiento, obtenidos mediante simulación para carga al 80 y al 120% de la carga promedio.
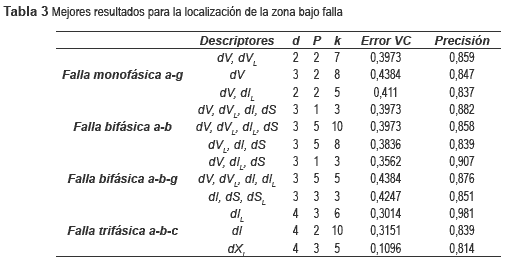
Los tres mejores resultados obtenidos para los todos los tipos de fallas se presentan en la tabla 3.
En este caso se aprecia una leve reducción del desempeño, si se realiza una comparación con el caso anterior. Se aprecia por tanto que la posibilidad de incluir nuevos datos en el conjunto de entrenamiento, a partir de un conjunto de datos nominales permite mantener el comportamiento de los dos casos anteriores. Sin embargo, se observa que sólo al adicionar más datos se obtienen mejores resultados. El problema asociado está relacionado con el tiempo computacional requerido y para evitarlo se utilizó la estrategia de reducción de Hart.
Caso 4. Doble parametrización con datos en condiciones nominales y adición de datos utilizando la condensación de Hart
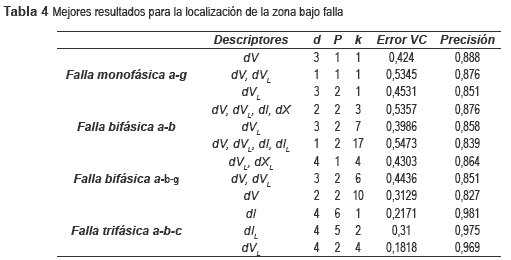
Este caso es similar al anterior, simplemente que se realiza una nueva parametrización luego que se han adicionado los datos utilizando la condensación de Hart. La precisión para este caso se calcula con los datos que no fueron utilizados en el entrenamiento, los cuales son los obtenidos de las bases de datos para carga al 80 y al 120% de la carga nominal. Los mejores resultados obtenidos para los diferentes tipos de fallas se presentan en la tabla 4.
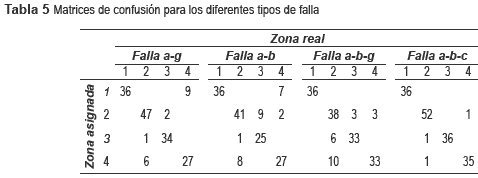
A partir de los resultados del caso 4, se infiere que no basta con aumentar la base de datos, sino que también se requieren calcular los nuevos parámetros para un mejor desempeño. En este caso, los resultados son los más adecuados, considerando todos los tipos de falla. Adicionalmente, en la tabla 5 se presentan las matrices de confusión, para la combinación de descriptores que obtuvo mejor desempeño.
En forma general y a partir de las pruebas realizadas, se observa que teniendo como entrada sólo la combinación de los descriptores de tensión de fase y de línea, se obtienen buenos resultados para los tipos de falla monofásica, bifásica y bifásica a tierra. Esto es importante porque permite una buena estimación del sitio de falla utilizando sólo medidas de tensión. Para fallas trifásicas las combinaciones que obtuvieron buenos resultados sólo utilizaron un descriptor como entrada entre dV, dS y dI. Adicionalmente, de la matriz de confusión se observa que en muy pocos casos se presentó confusión entre zonas no adyacentes.
Finalmente, se observa que el método de localización presenta buenos resultados cuando a partir de las bases de datos se interpola otros datos. Además, cuanto más aleatorio sean los datos escogidos para la parametrización el algoritmo tendrá una precisión menor.
Localización de fallas mediante el método de gráfico de reactancias
Como se explicó en la sección anterior, luego de localizar la zona en falla, se estima la distancia a la cual ésta ocurrió considerando el ramal específico. Para efecto de pruebas, en la figura 5 se presenta el error relativo calculado a partir de (7), para todos los nodos del sistema y considerando la falla monofásica a-g.
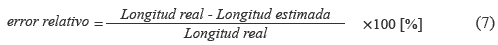
El ramal seleccionado para pruebas es el radial 1, que va desde la subestación hasta el nodo 302, con una longitud de 16 km.
Según la figura 5, el método se comporta relativamente bien para estimar la distancia a la falla, especialmente en caso de resistencias de falla inferiores a 15 Ω. En el caso de las fallas bifásica a-b, bifásica a tierra a-b-g y trifásica a-b-c, el error máximo es menor al 16%. Los resultados para el cálculo del error relativo en la estimación de la distancia utilizando el circuito radial 2 para todos los nodos, tienen un comportamiento similar a los del radial 1.
Conclusiones
La propuesta presentada en este artículo es una alternativa de fácil implementación y baja exigencia computacional, para aportar en la solución del problema de localización de fallas en redes de distribución de energía eléctrica. Esta estrategia integra un método clásico de estimación de la distancia, con una técnica intuitiva para determinar la zona en falla, lo cual soluciona el problema de la múltiple estimación y proporciona una localización confiable de la falla.
La metodología híbrida presentada es una buena aproximación a la solución del problema de localización de fallas en sistemas reales, ya que los errores obtenidos son bajos, aun cuando se consideran variaciones normales de la operación del sistema de potencia analizado. A partir de una base de datos con fallas obtenida normalmente por simulación, el método knn puede obtener buenos resultados de precisión, independientemente del tamaño del circuito analizado.
Finalmente, la técnica metaherística implementada como aporte original para la parametrización de la técnica de clasificación, permite obtener soluciones de alta calidad sin un gran esfuerzo computational.
Referencias
1. T. Short. ''Electric Power Distribution Handbook''. CRCpress. Vol. 1. 2003. pp. 8-30 [ Links ]
2. IEEE Std 37.114. ''IEEE Guide for Determining Fault Location on AC Transmission and Distribution Lines''. Power System Relaying Committee. Vol. 2004. pp. 1-36. [ Links ]
3. J. Mora. Localización de Fallas en Sistemas de Distribución de Energía Eléctrica usando Métodos Basados en el Modelo y Métodos Basados en el Conocimiento. Tesis Doctoral. University of Girona. Girona, España. 2006. pp. 21-86. [ Links ]
4. R. Das. Determining the locations of faults in distribution systems. Ph. D. dissertation. University of Saskatchewan. Saskatoon, Canada. 1998. pp 41-64. [ Links ]
5. A. Girgis, C. Fallon, D. Lubkeman. ''A fault location technique for rural distribution feeders'' IEEE Transactions on Industry and Applications. Vol. 26. 1993. pp. 1170-1175. [ Links ]
6. K. Srinivasan, A. St-Jacques. ''A new fault location algorithm for radial transmission lines with loads''. IEEE Transactions on Power Delivery. Vol. 4. 1989. pp. 1676-1682. [ Links ]
7. J. Mora, G. Morales, S. Pérez. ''Learning-based strategy for reducing the multiple estimation problem of fault zone location in radial power Systems''. IET Generation, Transmission & Distribution. Vol. 3. 2009. pp. 346-356. [ Links ]
8. R. Mahanty, P. Gupta. ''Application of RBF neural network to fault classification and location in transmission lines''. IEE Proceedings Generation, Transmission and Distribution. Vol. 151. 2004. pp. 201-212. [ Links ]
9. D. Thukaram, H. Khincha, H. Vijaynarasimha. ''Artificial Neural Network and Support Vector Machine Approach for Locating Faults in Radial Distribution Systems''. IEEE Transactions on Power Delivery. Vol. 20. 2005. pp. 710-721. [ Links ]
10. A. Moujahid, I. Inza, P. Larrañaga. Clasificadores knn. Departamento de Ciencias de la Computación e Inteligencia Artificial. Universidad del País Vasco- Euscal Herriko Unibertsitatea. Disponible en: http://www.sc.ehu.es/ccwbayes/docencia/mmcc/docs/t9knn.pdf. Consultado: Julio 2012. [ Links ]
11. S. Sivanandam, S. Deepa. Introduction to Genetic Algorithms. 1st ed. Ed. Springer Verlag. Heidelberg, Germany. 2003. pp 19-78. [ Links ]
12. P. Mitra, C. Murthy, S. Pal. ''Data condensation in large databases by incremental learning with support vector machines''. A. Sanfeliu, J. Villanueva, M. Vanrell, R. Alquezar, A. Jain, J. Kittler (editors). Proc. 15th Int. Conf. on Pattern Recognition. Vol. 2. 2000. pp. 708-711. [ Links ]
13. G. Morales, J. Mora, H. Vargas. ''Método de localización de fallas en sistemas de distribución basado en gráficas de reactancia''. Revista Scientia et técnica. Vol. 34. 2007. pp. 49-54. [ Links ]
14. J. Mora, J. Bedoya, J. Meléndez. ''Implementación de protecciones y simulación automática de eventos para localización de fallas en sistemas de distribución de energía''. Ingeniería y competitividad. Vol. 8. 2006. pp. 5-14. [ Links ]
15. V. Kecman. Learning and soft computing: Support Vector Machines, Neural Networks, and Fuzzy Logic Models. 1a ed. Ed. The M.I.T. Press. Cambridge, London. 2001. pp. 27-29. [ Links ]
16. B. Wang, Y. Zeng, Y. Yang. Generalized nearest neighbor rule for pattern classification. Proceedings of the 7th Congress on Intelligent Control and Automation. Chongqing, China. 2008. [ Links ]
17. J. Dagenhart. ''The 40-Ground-Fault Phenomenon''. IEEE Transactions on Industry Applications. Vol. 36. 2000. pp 30-32. [ Links ]