ARTÍCULO ORIGINAL

Simulación de la propagación de pulsos ópticos en guías de ondas microestructuradas

Simulation of optical pulse propagation in microstructured waveguides

Sonia Valbuena-Duarte^1*, Francisco Racedo-Niebles²

¹Grupo de Matemáticas e Informática de la Corporación Universitaria de la Costa de Ciencias Básicas (MATINCUC), Universidad de la Costa. Cra. 55 N.° 58-66. C.P. 080002. Barraquilla, Colombia.

²Grupo de Espectroscopía Óptica de Emisión y Laser (GEOEL), Facultad de Ciencias Básicas, Universidad del Atlántico. Km 7 Antigua Vía Puerto Colombia. C.P. 081007. Barranquilla, Colombia.

^*Autor de correspondencia: correo electrónico: fran@mail.uniatlantico.edu.co (F. Racedo)

(Recibido el 29 de julio de 2014. Aceptado el 30 de julio de 2014)

Resumen

Se estudia la propagación de pulsos ópticos por el método de diferencias finitas en guías de onda estructuradas tipo ridge para aplicaciones en sistemas de transmisión de óptica en la región de 1,55 m. Con la transformación de las ecuaciones de Maxwell de su forma continua a una formulación discreta para el sistema en estudio y con las condiciones de contorno apropiadas se implementó un algoritmo en Matlab que permitió visualizar el comportamiento del pulso al propagarse en la geometría del guía ridge. Se realizaron simulaciones variando la longitud de onda, el ancho de la región del núcleo y el índice de refracción de los materiales obteniéndose resultados similares a los reportados en la literatura. Este estudio permite proponer una geometría apropiada y sugerir materiales para confeccionar este tipo de guía de onda para aplicaciones en sistemas de comunicaciones ópticas.

Palabras Clave:Guía de onda, diferencias finitas, núcleo, frontera, algoritmo

Abstract

In this paper we study the propagation of optical pulses by the finite differences method in a ridge waveguides structured for applications in optical transmission systems in the region of 1.55 µm. With the transformation of Maxwell's equations its discrete formulation, for the system under study, and the appropriate boundary conditions was implemented an algorithm in Matlab geometry of the waveguide studied. Variations in simulation were made in the wavelength, width of the core and the refractive index materials with which the results obtained were consistent with those reported in the literature. This study allows proposing an appropriate geometry and materials for making waveguides for applications in optical communications systems.

Keywords:Waveguide, finite differences, core, boundary, algorithm

Introducción

El método de diferencias finitas, MDF, se fundamenta en aproximar las ecuaciones diferenciales de un problema determinado por ecuaciones de diferencias. Estas últimas se obtienen del truncamiento de la series de Taylor [1]. El sistema de ecuaciones en diferencias que se obtiene forma lo que se conoce como un sistema de ecuaciones lineales, el cual es susceptible de solucionarse computacionalmente de manera aproximada. En caso de que también exista dependencia temporal de las ecuaciones el método acostumbrase a denominar método de diferencias finitas en el dominio del tiempo, por sus siglas en ingles FDTD [2]. En este trabajo se aplicará el FDTD para analizar estructuras de confinamiento óptico como una guía de onda estructuradas tipo ridge [3] y estudiar la propagación del pulso óptico bajo diferentes condiciones. El estudio de guías de onda estructuradas en materiales cristalinos, tales como los semiconductores, es nuevo y de interés tecnológico ya que es deseable el poder contar con microestructuras confinantes que permitan disminuir el tamaño actual de los dispositivos sin comprometer su rendimiento [4]. Para esto se solucionan las ecuaciones de Maxwell en cierta región espacial Ω y ∂Ω su contorno , bajo condiciones iniciales en que si t=0, el valor de las funciones incógnitas u, para todos los puntos de la región espacial Ω obedecen la ecuación (1):

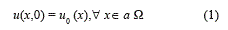
Esta condición de borde hace referencia a conocer en todo los instante de tiempo el valor de u, o de su derivada espacial ∂u/∂x, o de una combinación de ambas en la frontera ∂Ω de Ω. La resolución del problema consiste en hallar una función u = u(x; t) que sea continua en Ω + ∂Ω, y que sea diferenciable dos veces en Ω, y que cumpla con las condiciones iniciales y de borde [5]. La aplicación del método de las diferencias finitas se inicia con el muestreo en la región Q de un conjunto de puntos discretos, llamados malla o grilla, comúnmente denominado dominio computacional, y con una ventana de temporal de observación y un intervalo Δt de muestreo temporal definido. Seguidamente se aproxima la ecuación diferencial mediante una ecuación en diferencias. Posteriormente se evalúa la ecuación en diferencias en cada uno de los puntos de la malla y en la ventana temporal seleccionada. Finalmente, se resuelve numéricamente el sistema de ecuaciones lineales resultante que relacionan los campos en los distintos puntos o nodos de la malla. En términos simples el FDTD se basa en la discretización, tanto espacial como temporal, de los campos electromagnéticos y la posterior aproximación de las derivadas parciales, que aparecen en las ecuaciones rotacionales de Maxwell expresadas en el dominio del tiempo, por cocientes de diferencias finitas. Obteniéndose así un problema algebraico donde se calcula, en instantes sucesivos, el valor del campo eléctrico o magnético en cada punto del espacio a partir del valor del campo eléctrico o magnético en el mismo punto en el instante de tiempo anterior y de los valores del campo magnético o eléctrico en sus nodos adyacentes [5] Una de las ventajas del FDTD es que permite que se introduzca una perturbación en la estructura simulada y analizar la evolución tanto espacial como temporal del campo electromagnético en la misma [6].

Fundamentos matemáticos

Las ecuaciones rotacionales de Maxwell dependientes del tiempo, (2) y (3), en un medio lineal homogéneo e isotrópico son:

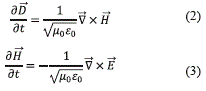
Donde µ₀ es la permeabilidad magnética y la permitividad eléctrica. Si se separan las ecuaciones rotacionales en sus componentes espaciales, se obtienen las ecuaciones (4) a (9).

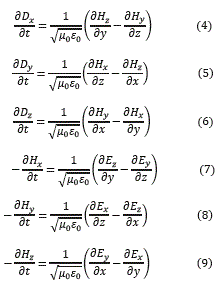
Sobre estas ecuaciones es que se implementa el FDTD.

En [7-9], se propuso un conjunto de ecuaciones en diferencias finitas para resolver el conjunto de ecuaciones de Maxwell. Para el caso tridimensional, objeto de este estudio, la región se divide en una red o grilla de celdas cubicas con coordenadas dadas por la ecuación (10).

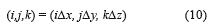
Identificando a Δx, Δy y Δz, como los incrementos espaciales. Con estos cada funcional dependiente del espacio y tiempo se puede escribir como se muestra en la ecuación (11).

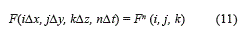
Siendo Δt, el intervalo de tiempo.

Ahora las derivadas espaciales y temporales de la función se implementan por medio de una aproximación en diferencias finitas centradas, dada por (12), evaluándolas en redes superpuestas.

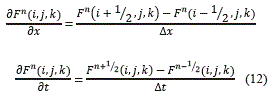
Al utilizar la ecuación (2) se evalúa el campo E en cada instante de tiempo n y con la ecuación (3) se evalúa el campo magnético H en cada instante de tiempo (n + 1/2).

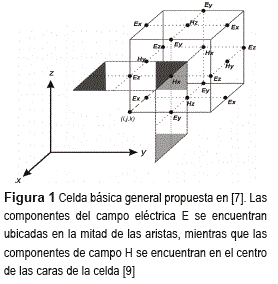
El método se basa en la utilización de las ecuaciones anteriores para calcular las derivadas de los campos electromagnéticos en las ecuaciones (4) a (9). Esto significa que el vértice de un cubo que pertenece a una grilla se encuentra en el centro de su cubo perteneciente a otra grilla como se muestra en la figura 1.

Al aplicar este método a las ecuaciones (4) a (9), se obtiene un sistema de ecuaciones en diferencias finitas. Esto permite transformar las ecuaciones ''continuas'' de Maxwell a una forma discreta. Por medio del algoritmo de diferencias centrales se obtienen de tres ecuaciones para el vector D, una para cada dirección x, y e z y tres para las componentes x, y e z del vector H. A manera de ejemplo se muestra la ecuación (13), en diferencias finitas correspondientes a la ecuación (4).

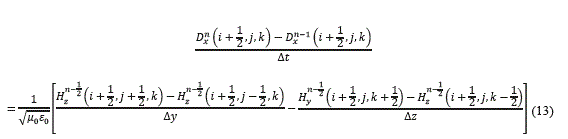
Similares ecuaciones se obtienen para las direcciones y, z de D. De forma similar la ecuación de las diferencias finitas (14) correspondiente a la ecuación (7) se muestra a continuación:

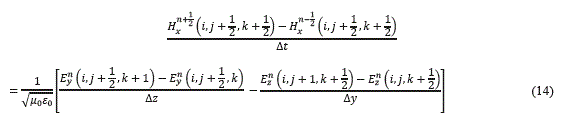
Similares ecuaciones se obtienen para las direcciones y, z de H.

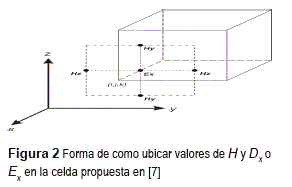
Estas dos ecuaciones, (13) y (14), y las cuatro faltantes similares,son las seis ecuaciones discretas en diferencias centrales en el espacio libre de las ecuaciones rotacionales de Maxwell. Como se puede observar, en la ecuación (13), los puntos utilizados para calcular D_x en un punto de la malla son las componentes de H_z^n-1/2 y H_y^n-1/2. Estos valores de H se encuentran ubicados en la mitad de las aristas de un cuadrado con orientación perpendicular al eje x y cuyo centro es el punto donde se calculará E_x, como se muestra en la figura 2 siguiente:

De manera similar se obtienen interpretaciones semejantes para D_y y D_z.

Para el caso de una onda electromagnética del tipo TE se tiene:

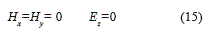
Sustituyendo en las ecuaciones (4) a (9) t teniendo en cuenta que D=εE y B=µ H sí; obtienen las ecuaciones de (16) a (18).

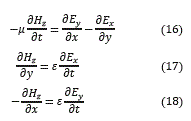
Para el casodeunaonda TM setiene la ecuación (19):

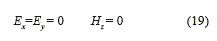
Sustituyendo en las ecuaciones (4) a (9), se obtienen las ecuaciones (20),(21) y (22).

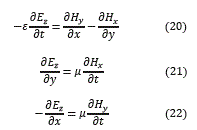
Las ecuaciones en diferencias finitas para las ondas TM y TE pueden escribirse de la forma:

Pata el raro de onda TE :

La expresión en diferencias finitas para la ecuación (16) se transforma en (23).

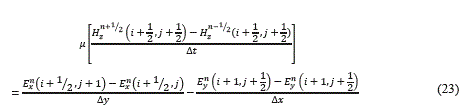
Despejando H_z^n+I/2 se tiene la ecuación (24) siguiente:

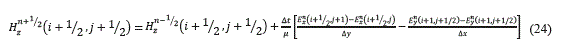
Utilizando el hecho de que en guías dieléctricas se definen los siguientes parámetros:

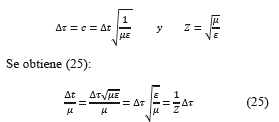
Sustituyendo estas en (24) se tiene la ecuación (26):

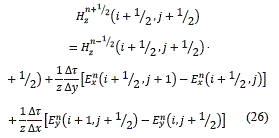
La ecuación (17) en diferencias finitas se expresa como muestra la ecuación (27):

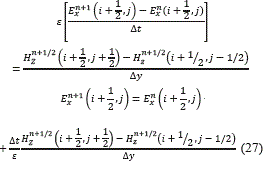
De (16) y (18) se tiene:

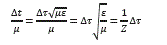
Permitiendo obtener la ecuación (28):

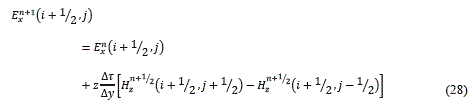
Para la ecuación (18) se obtiene la ecuación (29):

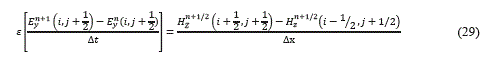
Reagrupando términos se obtiene (30):

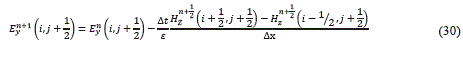
Simplificando se obtiene (31):

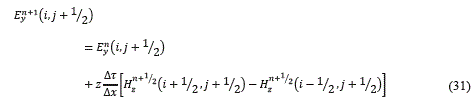
De manera similar se procede para ondas TM, obteniéndose el conjunto de ecuaciones dadas por (32):

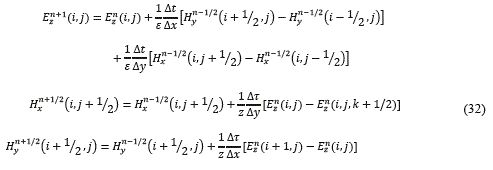
Recordando que D(ω)=ε_r(ω) E(ω), y utilizando el hecho de que se trabaja con un material dieléctrico, entonces esta expresión toma la forma dada en (33):

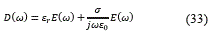
Si se transforma (33), del dominio de la frecuencia a un dominio temporal por medio del uso del análisis de Fourier se obtiene la ecuación (34):

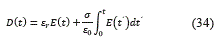
Para discretizar esta ecuación se aproxima por medio de una sumatoria la integral obteniendo (35):

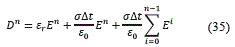
Si se despeja Eⁿ, se obtiene (36):

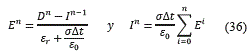
Esta elección permite elegir el tamaño de la celda espacial, posibilitando que la celda temporal quede determinada por (37):

Donde la constante c₀ representa la velocidad de la luz en el vacío.

Resultados y discusión

Una vez obtenidas las ecuaciones en diferencias finitas se implementó un algoritmo eficiente en Matlab para simular la propagación del pulso óptico en la guía microestructurada. Dentro del algoritmo se incluyeron rutinas tipo Absorving Boundary Condition (ABC), acopladas a Perfectly Matched Layers (PML), modificadas para evitar soluciones espurias. En este algoritmo se implementó una Graphic User Interface (GUI), que permite introducir y modificar parámetros tales como la longitud de onda, dimensiones geométricas del guía de onda como el ancho, altura y largo de las diferentes capas que conforman la guía de onda microestructurada, así como también modificar el valor del índice de refracción de las diferentes capas que conforman la microestructura. Esto permite obtener como respuesta las características espaciales del haz, así como el comportamiento modal de la estructura enfuncióndelos parámetros de entrada.

En la figura 3, se muestra una vista superficial de la microestructura del guía de onda propuesto. Se observan dos secciones de 21 rectángulos cada una, separadas por una región de aproximadamente de 2 µm. Las dimensiones de cada rectángulo son de 250 x 220 nm en dirección horizontal y en dirección vertical de la hoja respectivamente. En 3-D, estos rectángulos son paralelepípedos rectos. En el diseño los 42 rectángulos son del mismo material y en la GUI se introduce el índice de refracción del material escogido. El área entre los rectángulos es de un material distinto cuyo índice de refracción se introduce por medio de la GUI. Este material viene a configurar el núcleo de la guía de onda, como comúnmente se denomina la región guiante, que es la encargada de transportar la luz o el pulso electromagnético desde la entrada de la estructura, en el lado izquierdo de la hoja, hasta la parte derecha de la misma. El material del cual están hechos los rectángulos modifica el índice de refracción de la región donde estos se encuentran de tal forma que el valor promedio del índice de refracción de las regiones donde se encuentran ubicados los rectángulos es ligeramente mayor que el de la región del núcleo, permitiendo así confinar el pulso óptico en la región central. En el proceso de simulación en esta región central se observaron 4 lóbulos, dos blancos y dos oscuros, que representan la observación en diferentes instantes de tiempo y diferentes posiciones del pulso al propagarse. Se observa que para las condiciones estudiadas se consiguió un excelente confinamiento en la región del núcleo. También se observa, en el color, que el lóbulo oscuro que se encuentra a la derecha es de menor tonalidad y dimensión que los tres anteriores indicando que la intensidad del pulso ha decaído al propagarse a lo largo de la estructura. Esto debido a la absorción natural del material simulado a la longitud de onda estudiada.

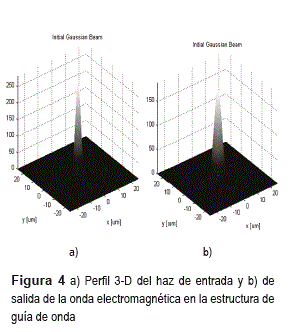
En la figura 4 siguiente se observan los perfiles 3-D del haz de entrada, izquierda, y en la salida, derecha, de la microestructura.

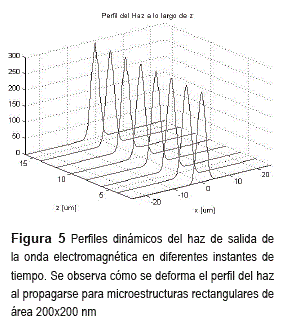
En la figura arriba, se observa que el perfil del haz de entrada es un poco más intenso que el de salida. Además se observa que el FWHM del perfil del haz de entrada es más estrecho que el del haz de salida. Esto es debido a que normalmente en sistemas de comunicaciones ópticas los haces que se utilizan corresponden a dispositivos láseres semiconductores que una vez enfocados en la región del núcleo de la guía de onda poseen un diámetro modal del orden de 2 a 3 µm [10, 11]. El FWHM, del perfil de salida a 80%, es de 4,5 µm en la dirección horizontal. Resultado este que concuerda con la dimensión horizontal simulada. Este resultado fue cuantificado por medio de las imágenes obtenidas que se muestran en la figura 5.

Para la simulacion de las microestructuras rectangulares con dimensiones horizontales iguales a 300 nm o mayores, manteniendo fija la dimension vertical en torno de 220 nm, se obtuvieron guias de ondas multimodales como se puede apreciar en la figura 6 a continuación.

En el caso de estructuras con dimensión horizontal de las microestructuras inferiores a 230 nm se obtuvo un comportamiento multimodal de la estructura reflejando condiciones de confinamiento pobres. Este comportamiento se debe principalmente a que con estas dimensiones, y menores, la región donde se encuentra embebidos las microestructuras rectangulares posee un índice de refracción medio muy similar al de la región guiante o núcleo. Hecho este que permite un pobre confinamiento del pulso.

Conclusión

El método FDTD es una herramienta útil y fácil de implementar para resolver problemas transitorios que se comportan según las ecuaciones de Maxwell. El algoritmo implementado con en el método FDTD es flexible y relativamente fácil de implementar. Una limitación presentada por el método es su estabilidad ya que depende de la grilla elaborada en el proceso de discretización y del tamaño del intervalo de tiempo utilizado para ejecutar los pasos en el tiempo.

En cuanto a la microestructura implementada para confinar la luz en la región guía o núcleo se consiguió determinar las dimensiones laterales apropiadas para un óptimo confinamiento del pulso al propagarse a lo largo de la estructura. Con estos datos geométricos se introdujo vía teclado valores de índice de refracción correspondientes a diferentes tipos de materiales permitiendo determinar cuál combinación de materiales era la apropiada para confeccionar la guía de onda. A través de estos ensayos se pudo determinar que el material ''base'' indicado es InGaAs con índice de refracción de 3.504 y el material de las microestructuras recomendado es InAlAs con índice de refracción de 3.354. Esta combinación de índices de refracción permite que la región confinante tenga un índice de refracción efectivo, calculado por el método de índice efectivo [9, 11, 12] de 3.490 apropiado para el confinamiento en la región núcleo y aplicación en la región de 1,55µm. Otra combinación de materiales apropiada para utilización en esta región de comunicaciones ópticas se basa en el uso de polímeros UV curables ópticos tal como el NOA61, que posee un índice de refracción de 1.547 y utilizada como núcleo de la guía de onda y el NOA81 utilizado para las microestructuras. Este último polímero posee un índice de refracción de 1.540 [12]. El índice efectivo de la región que confina la luz en el núcleo es de 1.540. Esta guía de onda es apropiada para uso en la región de transmisión de 1,55 µm. En este caso las dimensiones apropiadas para los paralelepípedos rectangulares obtenidas en la simulación es de 500x 500 nm. Si se comparan los dos materiales propuestos se recomienda implementar la guía de onda en material polimérico debido a que las técnicas de deposición de las películas de materiales poliméricos son de bajo costo comparadas con las técnicas de deposición de semiconductores. Además las dimensiones de las microestructuras a base de material polimérico son mayores y ofrecen mayor resistencia dinámica que las semiconductoras. De otro lado el tiempo de cómputo utilizado por el algoritmo es del orden de unos pocos segundos.

Referencias

1. K. Yee. ''Numerical solution of initial boundary value problem involving maxwell's equatios in isotropic media''. IEEE Transactions on Antennas and Propagation. Vol. 14. 1966. pp. 302-307.         [ Links ]

2. Z. Sacks, D. Kingsland, R. Lee, J. Lee. ''A perfectly matched layer anisotropic absorber for use as an absorbing boundary conditions''. SIAM. Vol. 512. 2012. pp. 317-337.         [ Links ]

3. D. Sullivan. Electromagnetic simulation using the FDTD method. 2^nd ed. Ed. IEEE Press. New York, USA. 2007. pp. 180-207.         [ Links ]

4. A. Taflove, S. Hagness. Computational electrodynamics the finite-difference time-domain method. 2^nd ed. Ed. Springer. 2012. pp. 245-282.         [ Links ]

6. F. Racedo, N. Torres. Teoría electromagnética. 1^st ed. Ed. Universidad del Atlántico. Barranquilla, Colombia. 2010. pp. 25-65.         [ Links ]

7. M. López, J. Gaspar, J. Manzanares. ''Aplicación del método de diferencias finitas en el dominio del tiempo a la simulación del campo electromagnético usando Matlab'' Revista Mexicana de Física. E 52. 2006. pp. 58-64.         [ Links ]

8. S. Valbuena, F. Racedo. Método de diferencias finitas en electromagnetismo. 1^st ed. Ed. EDUCOSTA. Barranquilla, Colombia. 2010. pp. 15-45.         [ Links ]

9. S. Nam, J. Kang, J. Kim, ''Direct pattering of polymer optical waveguided using liquid state UV-curable polymer''. Macromolecular Research. Vol. 14. 2006. pp. 114-116.         [ Links ]

10. U. Ascher and L. Petzold. ''Computer methods for ordinary differential equations and differential-algebraic equations''. SIAM. Vol. 137. 1998. pp. 121-138.         [ Links ]

11. J. Douglas, H. Rachford. ''On the numerical solution of heat conduction problems in two and three space variables''. Transactions ofthe American Mathematical Society. Vol. 82. 1956. pp. 421-439.         [ Links ]

12. C. Fletcher. Computational techniquess for fluid dynamics. 1^st ed. Ed. Springer-Verlag. Berlin, Germany. 1988. pp.125-132.         [ Links ]