ARTÍCULO ORIGINAL

Modelo de cálculo de las emisiones difusas de gases de efecto invernadero procedentes del transporte. Análisis según variables de diseño urbanístico

Calculation model for greenhouse gases diffuse emissions from transport. Analysis by urban design variabless

Sergio Zubelzu-Mínguez^1*, Alfonso Isidro López-Díaz², Miguel Ángel Gutiérrez-García², Fernando Blanco-Silva³

¹Departamento de Estadística e Investigación Operativa II (Métodos de Decisión), Facultad de Ciencias Económicas y Empresariales, Universidad Complutense de Madrid. Campus de Somosaguas. C.P. 28223. Pozuelo de Alarcón, España.

²Área Departamental Tecnológica, Facultad de Ciencias y Artes, Universidad Católica de Ávila. Calle Canteros, s/n. C.P. 05005. Ávila, España.

³Unidad Energía y Sostenibilidad, Universidad Santiago de Compostela, Campus Sur. Avenida de las Ciencias, 4. C.P. 15782. Santiago de Compostela, España.

^*Autor de correspondencia: Sergio Zubelzu Mínguez, correo electrónico: szubelzu@ucm.es

(Recibido el 05 de agosto de 2013. Aceptado el 04 de agosto de 2014)

Resumen

Entre las medidas más relevantes para frenar el calentamiento global se encuentra el control de las denominadas emisiones difusas, siendo las emisiones derivadas de las fuentes móviles una de las componentes más importantes dentro de tales emisiones. En el presente trabajo se han estudiado las emisiones difusas en el marco del diseño urbanístico y se han desarrollado métodos para el cálculo de las emisiones derivadas del tráfico rodado en función de parámetros de diseño urbanístico; como los usos del suelo, la longitud de viales o la edificabilidad, obteniendo así expresiones no lineales que permiten predecir los niveles de emisiones para diferentes usos. Los resultados muestran coeficientes de determinación de 0,644 para el uso residencial, 0,591 para el uso industrial, 0,592 para el uso terciario y 0,591 para los equipamientos, cifras de las que se deduce una mayor capacidad explicativa del modelo predictivo de las emisiones para el uso residencial.

Abstract

Control of diffuse emissions can be included among the most relevant actions aimed at breaking global warming. Emissions from road traffic join outstandingly in diffuse emissions. This paper studies these kind of emissions related to urban planning and proposes a model to calculate emissions, by using variables such as land use, vial length or edificability. Paper proposes nonlinear equations through emission levels for each land use can be estimated. Results show coefficient of determination of 0.644 for residential use, 0.591 for industrial, 0.592 for commercial and 0.591 for equipments. Figures that probe a higher explanatory power for model linked to residential uses.

Keywords: greenhouse emissions, carbon footprint, urban planning, diffuse emissions

Introducción

Con el fin de frenar el aumento de la concentración de Gases de Efecto Invernadero (GEI) los países más industrializados firmaron en 1997 el Protocolo de Kyoto, en el que se comprometían a reducir sus emisiones en el periodo 2008-2012 en un 5,2% en conjunto [1]. Con posterioridad a los acuerdos de Kyoto se habían celebrado diferentes cumbres sobre el clima (Montreal 2005, Bali 2007, Copenhague 2009, Cancún 2010, Durban 2011 y Doha 2012) en las que se ha venido acordando prolongar los objetivos del protocolo inicial. La conclusión más relevante de todas las anteriores pudiera ser el compromiso alcanzado en DOHA de tener preparado un nuevo acuerdo global contra el clima para el año 2015.

En España las primeras actividades obligadas a adoptar compromisos de control y reducción de emisiones fueron las incluidas en el Plan Nacional de Asignación [2]. Fuera de estas actividades concretas, existen un conjunto de sectores cuyas emisiones se denominan difusas que representan un volumen importante de las emisiones nacionales. Estos sectores son el transporte, los usos residenciales, los residuos, la actividad comercial o la industrial a pequeña escala. Es así que estas emisiones difusas alcanzan cierta relevancia en muchas regiones y se han estudiado de forma específica en relación al contexto urbano [3, 4]. Dentro de las fuentes difusas, las referidas a los sistemas de transporte también han sido objeto de diversas investigaciones entre las que cabe citar los trabajos de [5, 6]. Entre las fuentes de emisiones difusas, el tráfico rodado constituye una de las de mayor relevancia, como puede deducirse de los estudios de [7-9].

Por las razones expuestas, la correcta modelización y el consecuente control de las emisiones difusas en general, y de las procedentes de las fuentes móviles en particular, constituye una de las alternativas más potentes para la reducción de las emisiones globales. Entre las medidas que pueden adoptarse para propiciar la reducción de las emisiones procedentes de las fuentes móviles cabe distinguir dos clases: por un lado las medidas correctoras vinculadas con las emisiones ya existentes y por otro las preventivas orientadas al tráfico que se producirá como resultado de la ejecución del planeamiento urbanístico. El planeamiento urbanístico es la ordenación del crecimiento de las ciudades y una actividad de carácter transversal subyacente a las actividades económicas. Tiene una influencia determinante sobre las emisiones de GEI en general [10, 11] y sobre las difusas en particular al ordenar los transportes, la tipología de terrenos o la gestión de los residuos [12].

La principal ventaja de la vinculación del cálculo de las emisiones de GEI con el planeamiento urbanístico tiene que ver con la facilidad para implementar medidas para su reducción y compensación basadas en decisiones de diseño que el planeador puede adoptar en la línea, por ejemplo, de lo estudiado por [13] referido a los desarrollos industriales, [14] respecto de la intensidad residencial, [15] para el diseño urbano o incluso por [16] referido a las soluciones edificatorias. Estas decisiones pueden estar basadas, por ejemplo, en la reserva de terrenos no urbanizables o destinados al sistema de espacios libres y zonas verdes, ambas con efecto sumidero, o en el diseño sostenible de la red viaria de manera que se minimicen las emisiones.

Por consiguiente, el objetivo principal del presente trabajo ha sido desarrollar una herramienta predictiva que permita calcular las emisiones de GEI que se produzcan en los crecimientos urbanísticos en función de las variables de diseño urbanístico.

Experimentación

Para la consecución de dicho objetivo se ha seguido una metodología que ha implicado dar los pasos siguientes: i) Definir el contexto y el ámbito de aplicación del modelo; ii) seleccionar una región a partir de la cuál construir el modelo; iii) desarrollar una técnica para simular la generación y el reparto del tráfico; iv) desarrollar un modelo para el cálculo de las emisiones; v) construir el método que permita predecir las emisiones a partir de las variables explicativas.

Contexto y ámbito de aplicación

El instrumento básico de ordenación urbanística a nivel municipal en España es el denominado Plan General de Ordenación Municipal (o nomenclatura equivalente según la legislación concreta), documento que regula la acción urbanística general para todo el término municipal. En este documento se adoptan decisiones que poseen un efecto claro sobre las emisiones como son el modelo de ocupación del suelo (adscribiendo el territorio a alguna de las tres clases permitidas: urbano, urbanizable o rústico) o la definición de los usos del suelo (industrial, residencial, terciario) y de los sistemas generales (dotaciones, equiparables a los usos del suelo a los efectos del presente análisis, e infraestructuras que actúan como vector de las emisiones pero que no las generan de forma directa).

Se han considerado como entidades que deben soportar la determinación de las emisiones [17] aquellos ámbitos de desarrollo de suelo urbanizable en los que se proponen cada uno de los usos susceptibles de generar emisiones (residencial, industrial, terciario o dotacional). Para cada uno de estos cuatro tipos de ámbitos considerados como entidades se ha desarrollado una metodología que permite el cálculo de las emisiones derivadas del tráfico rodado a partir de las variables de diseño urbanístico que maneja el planeador.

Región objeto del estudio

Para construir el modelo se ha seleccionado una región de desarrollo económico homogéneo y con municipios económicamente interdependientes para evitar problemas derivados de los diferentes niveles de emisión identificados por [18]. Se ha buscado una región de municipios de tamaño medio cuyas emisiones han sido estudiadas en menor medida que para las grandes ciudades respecto de las que existe un mayor número de estudios como por ejemplo [19, 20].

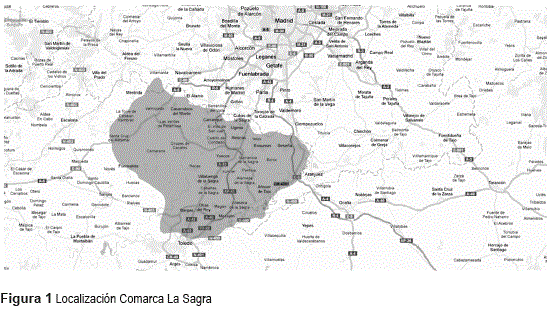
Tomando en consideración las premisas anteriores, se ha seleccionado la comarca de La Sagra ubicada en la Provincia de Toledo y que linda con la Comunidad de Madrid (Figura 1). Está compuesta por un total de 31 municipios que ocupan 700 km2 aproximadamente y cuentan con una población aproximada de 140.000 habitantes. Los municipios poseen una población que oscila entre valores mínimos próximos a 1.000 habitantes y máximos en la cercanía de los 15.000. Illescas y Seseña son los municipios de mayor tamaño y que constituyen el centro de actividad de la comarca.

Modelo de simulación del tráfico

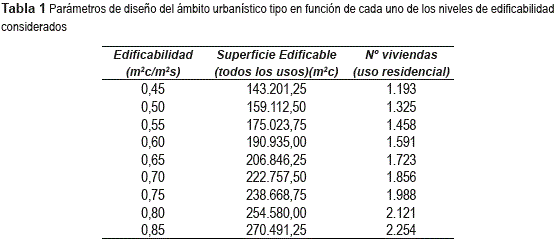
Para modelizar el tráfico se ha supuesto un desarrollo urbanístico testigo con una superficie de suelo de 318.225 m². La generación de tráfico de este desarrollo testigo se ha calculado bajo los supuestos de que su uso fuese residencial, industrial, terciario o dotacional y, para cada uno de estos cuatro supuestos, que el planeador propusiese diferentes valores de edificabilidad (m² construidos -m²c- por cada m² de suelo -m²s-) propios de la región en estudio. Las cifras que resultan de estos diferentes valores de edificabilidad quedan expresadas en la tabla 1.

Además, puesto que se trata de desarrollos urbanísticos testigo, se ha considerado que se localizasen en cada uno de los 31 municipios analizados y dentro de éstos, en las superficies potencialmente aptas para el crecimiento urbano. De esta forma se ha podido diferenciar entre la longitud interior al municipio (variable de diseño urbanístico al depender de los viales proyectados) y la exterior (variable ajena al diseño urbanístico) que habría de recorrerse para acceder a los potenciales destinos.

La simulación de los flujos de tráfico se ha basado parcialmente en propuestas existentes para estimar flujos de tráfico urbano como por ejemplo [21, 22]. El modelo de simulación del tráfico empleado en el presente trabajo asume que el flujo de movimientos entre dos zonas i, j (N_ij), es directamente proporcional a la generación tráfico en la zona origen i (g_i), a la atracción que ejerce cada zona destino j (a_j) y a la función de fricción (F(c_ij)) que representa el coste del desplazamiento entre las dos zonas. La expresión queda reflejada en la ecuación 1.

Cada uno de los tres componentes de la ecuación 1 se define en los puntos siguientes:

•    La función de fricción depende de la distancia entre el origen y el destino mediante la siguiente expresión (ecuación 2).

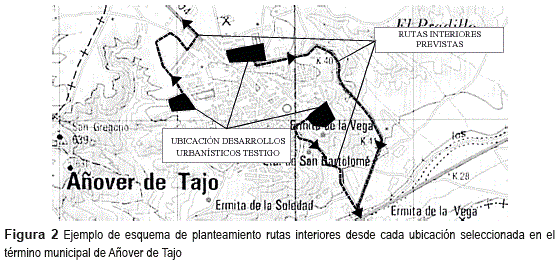
Donde d_ij representa la distancia desde el origen i al destino j y a el factor de fricción. Para la determinación del factor de fricción algunos autores han realizado ajustes estadísticos con diferentes funciones (exponenciales y potenciales principalmente), como por ejemplo [23-25]. De entre la relación de valores propuestos en la bibliografía, en el presente caso se ha adoptado un valor de 3,5 para minusvalorar el efecto de poblaciones alejadas pero con muchos habitantes (Madrid capital y su entorno especialmente). Para la consideración de la distancia recorrida se ha distinguido entre la distancia exterior al municipio de origen y la distancia interior al mismo. Las distancias exteriores han sido objeto de medición directa sobre plano a partir del trayecto de mínima distancia. Para el cálculo de la distancia interior se han trazado las rutas interiores al municipio que habrían de seguirse desde cada una de las hipotéticas ubicaciones del desarrollo testigo, para alcanzar las vías supramunicipales que conducen a los destinos. Sirva como ejemplo el expuesto en la figura 2 que representa algunas de las posibles ubicaciones del ámbito tipo y las rutas interiores que debieran recorrerse en Añover de Tajo.

Para la definición de la capacidad de atracción (a_j) deben definirse en primer lugar los posibles destinos de los movimientos generados. Se supone que el 90% de los movimientos son interiores al municipio y que el 10% restante podría dirigirse a cualquiera de los municipios ubicados en un radio de 70 km desde el municipio. El reparto entre cada uno de los municipios ubicados en este ámbito de influencia se realiza con arreglo a un coeficiente de reparto (r_j). Para definir este coeficiente de reparto, adoptando un criterio similar a [26], se asume que los movimientos exteriores pueden deberse a motivos laborales (se repartirán entre los diferentes destinos en función del número de empresas), de ocio (según el número de comercios) o personales (en función del tamaño de la población).

Para la asignación de pesos a cada uno de los motivos se ha recurrido a la Encuesta de Movilidad de las Personas Residentes en España [27]. Según los datos de la encuesta, agrupando los motivos de movilidad para un día laborable medio, se puede asumir que el 46,26 % de los movimientos se deben a motivos laborales, el 28,78% a personales y el 24,96 % a cuestiones de ocio. Así, la expresión final del coeficiente de reparto adopta la forma que se observa en la ecuación 3.

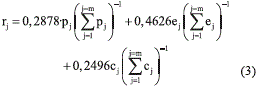
Donde p_j representa la población de cada uno de las posibles poblaciones destino, e_j hace referencia al total de empresas de cada uno de los posibles puntos destino y c_j alude al total de establecimientos comerciales.

•    En cuanto al tráfico generado en los ámbitos, algunos estudios proponen cifras para esta generación, como por ejemplo los realizados por [28] para tres distritos de la ciudad de Madrid o por [29] en el Estado de Florida. El Institute of Transportation Engineers (ITE) en su manual Trip Generation Handbook [30] incluye múltiples referencias para las tasas de generación de tráfico por usos adaptadas a las condiciones urbanísticas de los Estados Unidos. En el presente estudio se han adoptado las siguientes tasas de generación, adaptadas a partir de los datos expuestos por [28-30]:

- Uso residencial: 0,46 viajes de vehículo motorizado por persona residente (ocupación de 3 personas por vivienda). El 80% proceden de vehículos ligeros.

- Uso Terciario: 0,03 viajes/m² construidos (30% vehículos pesados).

- Uso Industrial: 0,014 viajes/m² construidos (80% vehículos pesados).

- Uso Dotacional: 0,016 viajes/m² construidos (15% vehículos pesados).

Todo el esquema anterior permite conocer el número de movimientos que desde cada uno de los 31 municipios analizados se dirigirá hacia cada uno de los municipios atractores incluidos en su zona de influencia. Conociendo este dato y la distancia entre cada uno de los municipios se puede calcular la longitud total recorrida por todos los movimientos que se generarían en el desarrollo urbanístico testigo.

Cálculo de las emisiones

La longitud recorrida es el dato base sobre el que calcular las emisiones de GEI mediante la aplicación de los factores de conversión oportunos. En el presente documento se han adoptado para estos factores los valores propuestos por el Department for Environment, Food and Rural Affairs (DEFRA) del Gobierno Británico [31] por considerarlos suficientes y acordes con el alcance deseado para el planeamiento general. En la publicación referida del DEFRA se incluyen valores promedio de emisiones de CO₂ equivalente (CO_2e) para vehículos pesados y para turismos en función del tipo de combustible. Estos factores se reproducen en la tabla 2.

En el presente estudio se ha adoptado el valor propuesto para los vehículos pesados sin más transformación. Para los turismos se ha calculado el promedio entre turismos diésel y gasolina al no disponerse de información específica del parque de vehículos en la región en estudio; el resultado final del factor de emisión para turismos es 0,238025 kgCO_2e/km. Con ello, los resultados definitivos de las emisiones imputables a cada uno de los ámbitos se obtienen aplicando los factores anteriores a la longitud recorrida por cada uno de los movimientos calculados.

Construcción del modelo predictivo

Para construir el modelo predictivo se han empleado técnicas estadísticas de regresión lineal 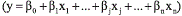y no lineal (logarítmica, inversa, cuadrática, cúbica, potencia, compuesto, logística, curva-S, crecimiento y exponencial) siendo las emisiones de GEI la variable explicada (y) y los parámetros de diseño urbanístico (edificabilidad, uso del suelo y longitud viaria), las explicativas (x_i).

Para el contraste del coeficiente de determinación se ha empleado el test F, mientras que para probar la validez de los coeficientes de regresión se ha utilizado el test t. La validez de estas dos técnicas se ha demostrado aún sin poder asumirse estrictamente la similitud de la distribución de los residuos de regresión con la distribución normal gaussiana [32].

Resultados y discusión

Se han realizado los cálculos de las emisiones de GEI que se generarían en cada uno de los 31 municipios y se han obtenido resultados, en función de cada uso del suelo, para las emisiones tanto interiores como exteriores al municipio e imputables tanto al tráfico ligero como al pesado. En un primer momento se han analizado los resultados de forma individual por municipios. Los resultados quedan expuestos en la figura 3.

En el gráfico expuesto en la figura 3 parece observarse que las emisiones más elevadas para cualquier uso del suelo aparecen vinculadas en general a dos tipos de municipios. El primer tipo lo constituyen los municipios de mayor tamaño como son Illescas, Seseña o Yuncler en los que las distancias interiores que deben recorrer los vehículos son relevantes de cara a las emisiones. El segundo tipo está formado por municipios de menor tamaño pero más alejados de los principales municipios que atraen los movimientos, como por ejemplo los municipios de Olías del Rey o Carranque. En este segundo tipo de municipios los trayectos exteriores adquieren mayor relevancia que los interiores sobre el nivel de emisiones.

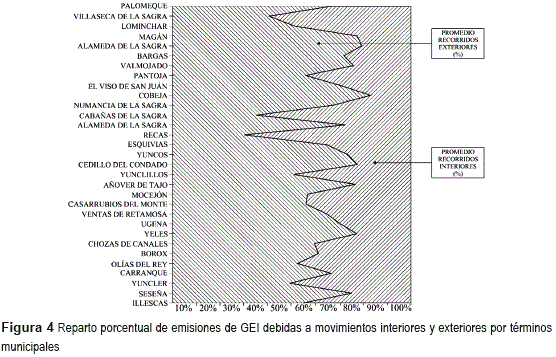
Aun habiendo supuesto que la mayor parte de los movimientos son interiores al municipio, las mayores distancias que se consideran para el cálculo de las emisiones exteriores hacen que éstas sean las más relevantes en muchos de los casos como se deduce de lo expresado en la figura 4.

Véase cómo los municipios de Illescas o Yuncler poseen un mayor peso de los desplazamientos interiores sobre las emisiones, al contrario que Carranque u Olías del Rey.Los casos de Magán y Añover del Tajo son singulares por cuanto están afectados por la presencia muy próxima de un municipio de considerable relevancia que atrae la mayor parte de los movimientos que generan, lo que justifica que las emisiones derivadas de las distancias interiores pudiesen llegar a ser mayores que las exteriores incrementándose así el peso de las emisiones interiores.

También resulta singular el caso del municipio de El Viso de San Juan por cuanto, aunque se trata de un municipio de pequeño tamaño, posee un modelo de ocupación del suelo basado en urbanizaciones dispersas lo que incrementa las distancias recorridas en el interior del municipio.

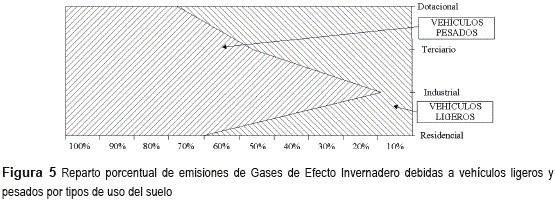
Si el análisis se centra en el reparto de las emisiones imputables a cada tipo de vehículo, los resultados muestran una clara dominancia de las emisiones derivadas de los vehículos pesados en los usos industrial y terciario, al contrario que en los usos residencial y dotacional. Estas proporciones están reflejadas en la figura 5.

Para la construcción del modelo de predicción a partir de los datos anteriores cabe observar en un primer lugar las relaciones entre las variables independientes y dependiente. La tabla 3 muestra los resultados de las emisiones de GEI distinguiendo entre usos. Se trata de valores promedio para los 31 municipios considerados y para las distancias interiores calculadas derivadas de cada una de las localizaciones propuestas.

Los datos expuestos en la tabla 3 muestran una mayor relevancia de las emisiones de GEI vinculadas a los usos industriales y terciarios frente a los dotacionales y residenciales. Resultados similares a los obtenidos por [18].

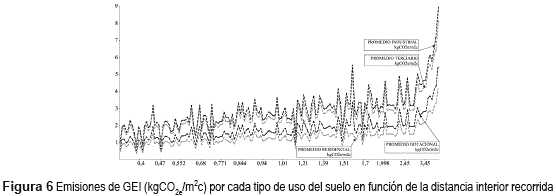
La figura 6 expuesta a continuación muestra las emisiones (resultados promedio para todos los valores de edificabilidad) vinculadas a cada una de las distancias interiores calculadas para cada uno de los 31 municipios.

El gráfico expuesto en la figura 6 muestra una clara relación creciente, percibiéndose de nuevo los mayores valores referidos a los usos terciario e industrial frente a los residenciales y dotacionales. El patrón de comportamiento observado en la figura 6 se repite cuando los resultados se filtran para cada uno de los niveles de edificabilidad. Esta afirmación se comprueba fácilmente analizando los coeficientes de correlación lineal entre las emisiones referidas a cada tipo de uso y la distancia que se muestran en la tabla 4.

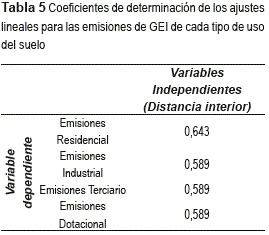
Los coeficientes expuestos en la tabla 4 muestran una intensidad de la relación lineal elevada lo que constituye un adecuado punto de partida para aplicar las técnicas de regresión lineal. La tabla 5 muestra los resultados del coeficiente de determinación (R2) para cada uno de los ajustes lineales realizados.

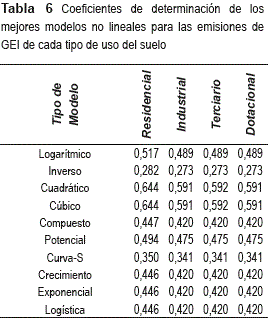
A pesar de las elevadas cifras expuestas en la tabla 5, los resultados para el coeficiente de determinación de cada uno de los ajustes no lineales muestran una mayor capacidad explicativa en los modelos cúbico y cuadrático frente a los modelos lineales, como se deduce de los datos incluidos en la tabla 6.

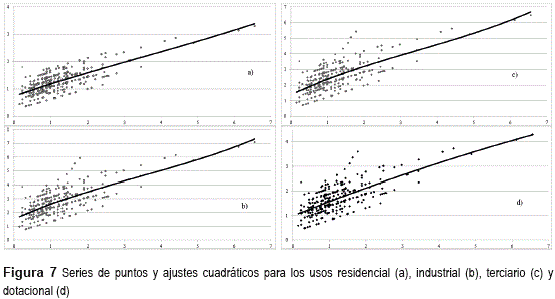
Como puede observarse en las tablas 5 y 6, los modelos cúbico (y=β₀+(β₁x₁)+ (β₂x₁²)+ (β₃x₁³)) y cuadrático (y=β₀+(β₁x₁)+ (β₂x₁²)) proporcionan una capacidad explicativa mayor que los modelos lineales. De entre los dos modelos referidos, a la vista de la similitud entre los coeficientes de determinación, se ha optado por seleccionar el modelo cuadrático debido a su mayor simplicidad. La figura 7 muestra los puntos observados y el ajuste cuadrático para cada uno de los usos.

Si la mayor capacidad explicativa del modelo cuadrático se analiza a la vista del gráfico incluido en la figura 6, cabe achacar la componente de orden 2 del modelo a las emisiones derivadas de los municipios en los que las distancias interiores son más elevadas. El gráfico expuesto en la figura 7 muestra como la tendencia se asemeja a la lineal hasta un valor de la distancia interior recorrida próxima a los 3 km, valor por encima del cual el incremento de emisiones se torna potencial.

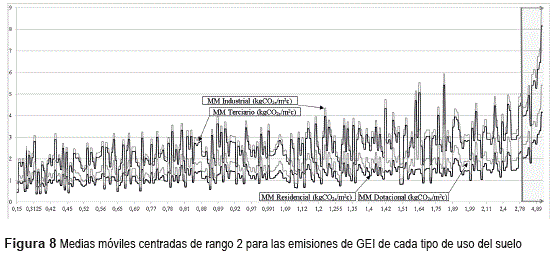
Este comportamiento se observa con mayor claridad en la figura 8 en la que se han representado las medias móviles centradas de rango 2 para cada uno de los tipos de emisiones, marcando la zona de la serie que justifica la componente cuadrática.

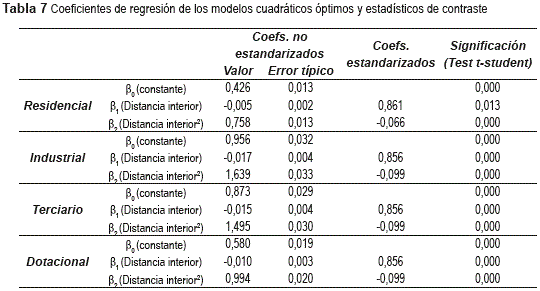
Para la concreción definitiva de los modelos quedan pendientes de presentar los coeficientes de regresión de cada uno de ellos. En la tabla 7 se incluyen tanto los valores para estos coeficientes como los estadísticos propios de cada uno de ellos.

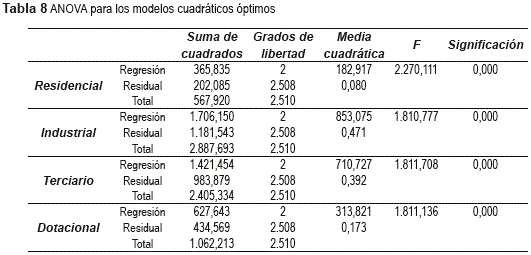
Como puede observarse en la tabla 7, todos los resultados obtenidos son significativos para un nivel de confianza del 95%, mientras que si el nivel de confianza se fija en el 99% únicamente para el coeficiente β₁ del ajuste para el uso del suelo residencial sería imposible descartar su nulidad, aunque por un pequeño margen. Los cálculos del ANOVA expuestos en la tabla 8 permiten excluir la nulidad del coeficiente de determinación para un nivel de confianza del 99%.

Conclusiones

El modelo propuesto en el presente trabajo permite incorporar el cálculo de las emisiones de GEI vinculadas al tráfico rodado de forma sencilla en el proceso de planeamiento urbanístico. Las expresiones obtenidas permiten al planeador conocer el nivel de emisiones vinculado a cada decisión de planeamiento sin más que conocer la longitud viaria prevista para cada desarrollo.

Este ejercicio garantiza la sostenibilidad en el diseño urbano desde las fases de planeamiento general hasta la ejecución urbanística y edificatoria. La herramienta desarrollada en el presente trabajo permite además adoptar medidas de reducción y compensación mediante la implementación de superficies destinadas a la fijación de los contaminantes emitidos, el modelo de ocupación del suelo, los usos previstos o el diseño de la trama viaria.

El modelo de cálculo propuesto en el presente trabajo permite además analizar la sensibilidad de las emisiones de GEI ante variaciones de los parámetros de diseño urbanístico: usos del suelo, edificabilidad, longitud viaria o modelo de ocupación del suelo.

Respecto de los resultados concretos del estudio, los niveles de emisión de GEI son superiores en los usos industriales y terciarios. En estos dos tipos de usos del suelo las emisiones son mayoritariamente debidas a los vehículos pesados, al contrario que en los usos residencial y dotacional en los que resultan más relevantes las emisiones debidas a los vehículos ligeros.

Los mayores niveles de emisión aparecen vinculados a municipios de tamaño elevado y con grandes distancias interiores o a municipios que, independientemente del tamaño, se encuentran alejados de los principales focos atractores de movimientos. Las mayores distancias interiores derivadas del mayor tamaño de los municipios o de modelos extensivos de ocupación del suelo tienen un efecto potenciador de las emisiones y justifican la mayor capacidad explicativa de los modelos cuadráticos y cúbicos frente a los lineales.

En cuanto a los modelos de predicción de las emisiones, la distancia interior como variable dependiente ha mostrado una capacidad explicativa adecuada. Los ajustes con mayor capacidad explicativa han sido los modelos no lineales cúbico y cuadrático para todos los tipos de uso. El modelo óptimo se ha considerado el cuadrático cuya capacidad explicativa alcanza el 64,4% de la varianza de las emisiones para el uso residencial, el 59,1% para los usos dotacional e industrial y un 59,2% para las emisiones en los usos terciarios.

Referencias

1. P. Restrepo, D. Tobón, J. Flórez. ''Institucionalidad en torno a los mercados decarbono y los mecanismos de flexibilización derivados del Protocolo de Kioto''. Revista Facultad de Ingeniería Universidad de Antioquía. Vol. 46. 2008. pp. 46-57.         [ Links ]

2. J. Císcar. ''El mercado europeo de emisiones de gases de efecto invernadero y la economía española''. Economistas. Vol. 104. 2005. pp. 126-134.         [ Links ]

3. J. Lin, Y. Liu, F. Meng, S. Cui, L. Xu. ''Using hybrid method to evaluate carbon footprint of Xiamen City, China''. Energy Policy. Vol. 58. 2013. pp. 220-227.         [ Links ]

4. S. Puliafito, D. Allende. ''Patrones de Emisión de la Contaminación Urbana''. Revista Facultad de Ingeniería Universidad de Antioquia. Vol. 42. 2007. pp. 38-56.         [ Links ]

5. S. Sharma, S. Mishra. ''Intelligent Transportation Systems-Enabled Optimal Emission Pricing Models for Reducing Carbon Footprints in a Bimodal Network''. Journal of Intelligent Transportation Systems. Vol. 17. 2013. pp. 54-64.         [ Links ]

6. A. Mathez, K. Manaugh, V. Chakour, A. El-Geneidy, M. Hatzopoulou. ''How can we alter our carbon footprint? Estimating GHG emissions based on travel survey information''. Transportation. Vol. 40. 2013. pp. 131-149.         [ Links ]

7. R. Fernández, E. Valenzuela. ''Gestión ambiental de tránsito: cómo la ingeniería de transporte puede contribuir a la mejoría del ambiente urbano''. Eure. Vol. 30. 2004. pp. 97-107.         [ Links ]

8. H. Romero, F. Irarrázaval, D. Opazo, M. Salgado, P. Smith. ''Climas urbanos y contaminación atmosférica en Santiago de Chile''. Eure. Vol. 36. 2010. pp. 35-62.         [ Links ]

9. E. Hertwich, G. Peters. ''Carbon Footprint of Nations: A Global, Trade-Linked Analysis''. Environmental Science and Technology. Vol. 43. 2009. pp. 6414- 6420.         [ Links ]

10. D. Engel, S. Petsch, H. Hagen, S. Guhathakurta. ''Neighborhood relation diagrams for local comparison of carbon footprints in urban planning''. Information Visualization. Vol. 11. 2012. pp. 124-135.         [ Links ]

11. S. Petsch, S. Guhathakurta, L. Heischbourg, K. Muller, H. Hagen. ''Modeling, Monitoring, and Visualizing Carbon Footprints at the Urban Neighborhood Scale''. Journal of Urban Technology. Vol. 18. 2011. pp. 81- 96.         [ Links ]

12. R. Farreny, J. Oliver, M. Montlleó, E. Escribá, X. Gabarrell, J. Rieradevall. ''The ecodesign and planning of sustainable neighbourhoods: the Vallbona case study (Barcelona)''. Informes de la Construcción. Vol. 63. 2011. pp. 115-124.         [ Links ]

13. H. Dong, Y. Geng, F. Xi, T. Fujita. ''Carbon footprint evaluation at industrial park level: A hybrid life cycle assessment approach''. Energy Policy. Vol. 57. 2013. pp. 298-307.         [ Links ]

14. T. Kim, H. Kim. ''Analysis of the effects of intra-urban spatial structures on carbon footprint of residents in Seoul, Korea''. Habitat International. Vol. 38. 2013. pp. 192-198.         [ Links ]

15. C. Ho, Y. Matsuoka, J. Simson, K. Gomi. ''Low carbon urban development strategy in Malaysia - The case of Iskandar Malaysia development corridor''. Habitat International. Vol. 37. 2013. pp. 43-51.         [ Links ]

16. P. La Roche. ''Calculating greenhouse gas emissions for buildings: analysis of the performance of several carbon counting tools in different climates''. Informes de la Construcción. Vol. 62. 2010. pp. 61-80.         [ Links ]

17. British Standards Institution (BSI). Guide to PAS 2050: How to assess the carbon footprint of goods and services. 1st ed. Ed. BSI. London, UK. 2008. pp. 56.         [ Links ]

18. Y. Wang, N. Li. ''The provincial carbon footprint and trade''. Advanced Materials Research. Vol. 524-527. 2012. pp. 3514-3518.         [ Links ]

19. B. Sovacool, M. Brown. ''Twelve metropolitan carbon footprints: A preliminary comparative global assessment''. Energy Policy. Vol. 38. 2010. pp. 4856- 4869.         [ Links ]

20. S. Ganga, B. Gurjar, R. Kumari. ''Urban and country level greenhouse gas emissions and carbon footprints: A comparative study of a megacity, Delhi and India''. Journal of environmental science & engineering. Vol. 53. 2011. pp. 137-142.         [ Links ]

21. L. Willumsen. ''Modelos simplificados de transporte urbano''. Eure. Vol. 12. 1985. pp. 49-64.         [ Links ]

22. C. Lizárraga. ''Expansión metropolitana y movilidad: el caso de Caracas''. Eure. Vol. 38. 2012. pp. 99-125.         [ Links ]

23. C. González, I. Sarmiento. ''Modelación de la distribución de Viajes en el Valle de Aburrá utilizando el modelo gravitatorio''. Dyna. Vol. 76. 2009. pp. 199- 208.         [ Links ]

24. C. González, I. Sarmiento. ''Análisis de la modelación de la distribución de viajes para diferentes categorías socioeconómicas en el Valle de Aburrá''. Revista Facultad de Ingeniería Universidad de Antioquia. Vol. 64. 2012. pp. 115-125.         [ Links ]

25. M. Valdivia, H. Ávila, C. Galindo. ''Fricción de la distancia, autocorrelación espacial de la productividad e impacto de la longitud por carretera en la dinámica de convergencia de la región centro de México (1993- 2003)''. Investigaciones Geográficas. Vol. 71, 2010. pp. 72-87.         [ Links ]

26. C. González, I. Sánchez, J. Holguín. ''An empirical investigation on the impacts of spatial and temporal aggregation on empty trips models''. Revista Facultad de Ingeniería Universidad de Antioquia. Vol. 64. 2012. pp. 150-162.         [ Links ]

27. J. Ropero. Encuesta de Movilidad de las Personas Residentes en España. Ministerio de Fomento. Madrid, España. 2008. pp. 474.         [ Links ]

28. C. López, M. Delgado, D. Hoz Sánchez, A. Monzón. Relación existente entre la producción de viajes en el municipio de Madrid y los usos urbanísticos. Actas del VIII Congreso de Ingeniería de los Transportes. A Coruña, España. 2008. pp. 267.         [ Links ]

29. R. Ewing, M. Deanna, L. Shi-Chiang. ''Land Use Impacts on Trip Generation Rates''. Transportation Research Record: Journal of the Transportation Research Board. Vol. 1518. 2007. pp. 1-6.         [ Links ]

30. Institute of Transportation Engineers. Trip Generation Handbook. 2nd ed. Ed. Institute of Transportation Engineers. Washington, USA. 2004. pp. 164.         [ Links ]

31. Department of Energy and Climate Change; Department for Environment, Food and Rural Affairs. Guidelines to Defra/DECC's GHG Conversion Factors for Company Reporting. Ed. DECC, Defra. Londres, UK. 2011. pp. 85.         [ Links ]

32. D. Gujarati. Basic Econometrics. 5^th ed. Ed. McGraw- Hill. New York, USA. 1995. pp. 838.         [ Links ]