ARTÍCULO ORIGINAL

Uso de lógica difusa para la administración de un sistema disipador de energía en estructuras compuesto por amortiguadores magnetoreológicos

Use of fuzzy logic for the administration of a structural control system based on magnetorheological dampers

Luis Augusto Lara-Valencia^1*, Yamile Valencia-Gonzalez¹, José Luis Vital de Brito²

¹ Departamento de Ingeniería Civil, Universidad Nacional de Colombia (Sede Medellín). Carrera 80 N.° 65-223, Núcleo Robledo. Medellín, Colombia.

² Departamento de Engenharia Civil e Ambiental, Universidade de Brasília. Campus Universitário Darcy Ribeiro. CEP. 70910-900. Brasília, Brasil.

* Autor de correspondencia: Luis Augusto Lara Valencia, correo electrónico: lualarava@unal.edu.co

(Recibido el 23 de agosto de 2013. Aceptado el 10 de julio de 2014)

Resumen

Los amortiguadores magnetoreológicos son mecanismos disipadores de energía que desarrollan fuerzas de control variables útiles para la administración de sistemas estructurales sujetos a excitaciones dinámicas. Estos dispositivos son generalmente regidos por algoritmos complejos y sofisticados que necesitan de un gran poder de procesamiento. En este artículo se plantea el uso de un algoritmo de control fundamentado en lógica difusa, el cual realiza ajustes en la señal de comando de amortiguadores magnetorreológicos de forma simple y rápida basado en el conocimiento heurístico que se tenga de la estructura. A partir de un ejemplo numérico desarrollado, fue posible determinar que el proyecto de control propuesto se mostró suficientemente competente y confiable para administrar fuerzas de control, consiguiendo reducciones de picos de respuesta hasta de un 68%.

Palabras Clave: dinámica de estructuras, control semi-activo de estructuras, lógica difusa, amortiguadores magnetoreológicos

Abstract

Magnetorheological dampers are energy dissipation devices that develop variable control forces useful for the administration of structural systems under the effect of dynamic loads. In general, these devices are governed by complex and sophisticated algorithms that required a high processing power. This paper proposes the use of a control algorithm based on fuzzy logic which makes adjustments to the command signal of magnetorheological dampers in a simple and faster way based on the heuristic knowledge of the structure analyzed. From a numerical example was possible to establish that the proposed control project was competent and reliable enough to manage control forces, achieving peak of responses reductions up to 68%.

Keywords: dynamic of structures, semi-active control of structures, fuzzy logic, magnetorheological dampers

Introducción

El control de sistemas estructurales es un área de conocimiento que ha venido cobrando gran protagonismo en los últimos años, esto debido principalmente a la materialización de estructuras elevadas y de gran esbeltez, que tienen el propósito de ser lugares seguros y confortables para la ocupación humana, incluso ante el efecto de fenómenos ambientales fuertes de tipo transitorio. Para tal fin, estos sistemas precisan de herramientas que faciliten la disipación de energía y alivien las posibles consecuencias que se puedan generar en este tipo de situaciones.

Uno de los mecanismos con mayor potencial de auxiliar y proteger sistemas estructurales ante eventos circunstanciales, son los amortiguadores magnetoreológicos, dispositivos con la capacidad de administrar fuerzas de control variables. Su funcionamiento se basa en la polarización de partículas magnéticas micrométricas que restringen el flujo de un fluido especial confinado en un cilindro hidráulico, con lo que se desarrollan fuerzas fluctuantes que dependerán directamente del campo magnético aplicado en el dispositivo.

A pesar de lo promisorio de estos dispositivos, su puesta en funcionamiento presenta un gran obstáculo, la dificultad para implementar en tiempo real los algoritmos administradores del sistema estructura-controlador debido a la complejidad del problema, la difícil y dispendiosa solución matemática del mismo, y la gran cantidad de datos y variables que necesitan ser procesados.

Debido a esto, en el presente artículo se propone una metodología sencilla, basada en lógica difusa, que define la señal de comando adecuada a ser empleada en amortiguadores magnetoreológicos, con el objetivo de generar fuerzas de control que reduzcan de forma eficiente, rápida y segura las solicitaciones de sistemas estructurales sometidos a la acción de cargas transitorias.

Amortiguadores magnetoreológicos

Los amortiguadores magnetorreológicos (MR) son controladores estructurales de tipo semi-activo. Estos dispositivos se caracterizan por utilizar un líquido ajustable, denominado fluido magnetoreológico, cuya principal particularidad es su capacidad para modificar su viscosidad al ser expuesto a un campo magnético. Cuando estos fluidos se encuentran en su estado natural son tratados como fluidos Newtonianos. No obstante, si un campo magnético es aplicado, la idealización teórica que más se ajusta al comportamiento descrito por este tipo de fluido es el modelo visco-plástico.

El fluido MR está compuesto de partículas micrométricas magnéticamente polarizables que están dispersas en un medio portante de consistencia oleosa [1]. Generalmente, este tipo de fluidos son líquidos de flujo libre, sin embargo, en presencia de un campo magnético, las partículas magnéticas adquieren un momento dipolar que se alinea con el campo externo provocando que las partículas formen cadenas lineales paralelas a dicho campo.

Una vez constituidas las cadenas formadas a partir de la unión de las partículas magnéticamente polarizables, el movimiento del líquido se ve restringido, aumentando así la resistencia al flujo. La rata de cambio estará directamente relacionada a la magnitud del campo magnético aplicado y puede ocurrir en pocos milisegundos.

A pesar de que el descubrimiento y los primeros desarrollos de fluidos MR se hayan dado en los años 1940 con los trabajos pioneros del ingeniero e inventor Jacob Rabinow [2,3 y 4], solo recientemente se han venido aprovechando las características especiales de este tipo de fluidos para estudios y aplicaciones en el campo del control de vibraciones en estructuras civiles, específicamente aprovechando el control de flujo del fluido MR para administrar fuerzas de amortiguamiento en dispositivos disipadores de energía construidos con base en este líquido.

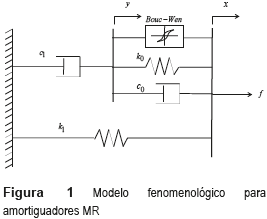
Es posible encontrar en la literatura diversos modelos que describen de manera más o menos adecuada el comportamiento numérico de los amortiguadores MR. Sin embargo, generalmente es resaltado que uno de los modelos que demostró mayor precisión emulando el desempeño real de este tipo de dispositivos, es un modelo paramétrico conocido como modelo fenomenológico [5]. El modelo fenomenológico es un modelo de Bouc-Wen modificado, el cual está compuesto por un amortiguador posicionado en serie con el modelo de histéresis original de Bouc-Wen y un resorte ubicado en paralelo con el sistema entero. La figura 1 presenta un esquema del modelo fenomenológico que será utilizado para el desarrollo del proyecto de control estructural propuesto.

El modelo fenomenológico puede ser divido en dos partes con el objetivo de obtener las ecuaciones que rigen el comportamiento del disipador. Si se considera solamente la sección superior del modelo se obtiene la ecuación (1):

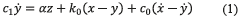
Donde c₁ es un coeficiente de amortiguamiento, incluido en el modelo con el objetivo de reproducir el comportamiento observado a bajas velocidades; y^. es la velocidad del amortiguador con coeficiente de amortiguamiento c₁; α es un factor de escala; k₀ y c₀ son, respectivamente, parámetros que controlan la rigidez y el amortiguamiento del sistema a grandes velocidades; (x-y) y 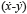son, respectivamente, el desplazamiento y la velocidad relativa que aplica al modelo de Bouc-Wen, al resorte con constante de rigidez k₀ y al amortiguador con coeficiente de amortiguamiento c₀. Finalmente, el coeficiente z es la variable histerética del modelo de Bouc-Wen, la cual está definida por la expresión (2):

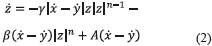
Donde A, n, β y γ son parámetros constantes del modelo, sugeridos comúnmente en la literatura.

Si la ecuación (1) se resuelve en términos de 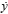, es posible obtener la ecuación (3):

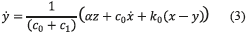
Para determinar el valor de la fuerza total f generada por el sistema, basta sumar las contribuciones de la sección superior e inferior del modelo fenomenológico. De esta manera, es posible deducir la ecuación (4):

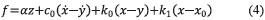
Donde k₁ representa la rigidez del acumulador y x₀ simboliza el desplazamiento inicial del resorte con rigidez k₁, asociado con la fuerza nominal de amortiguamiento debida al acumulador del amortiguador.

Si se sustituye la ecuación (1) en la ecuación (4), se tendrá la ecuación (5):

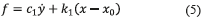
Lógica difusa

El concepto de lógica difusa fue concebido por el profesor Lofti A. Zadeh en los años 1960, con el objetivo de proporcionar fundamentos que permitieran utilizar razonamiento aproximado, a través de proposiciones imprecisas basadas en la teoría de conjuntos difusos, de forma análoga como el razonamiento clásico utiliza proposiciones precisas basadas en la teoría de conjuntos clásica [6]. De esta manera, la lógica difusa ofrece una inferencia matemática que permite aproximar las capacidades del raciocinio humano para ser utilizadas en problemas en que se tenga un conocimiento amplio y suficiente del sistema analizado, permitiendo modelaciones complejas mediante la representación y manipulación de conocimientos imperfectamente descritos, vagos o imprecisos [7].

La lógica difusa ha demostrado ser una herramienta efectiva en la solución de problemas de control, pues a partir de datos reales del desempeño de un sistema, es posible inferir un conjunto de funciones o de parámetros clasificatorios que permiten determinar una acción de control a efectuar. Con esto, el proyecto de control se simplifica mucho, evitando de esta manera la solución de ecuaciones diferenciales, la utilización de artificios matemáticos complejos y reduciendo el gasto computacional propio de problemas de control.

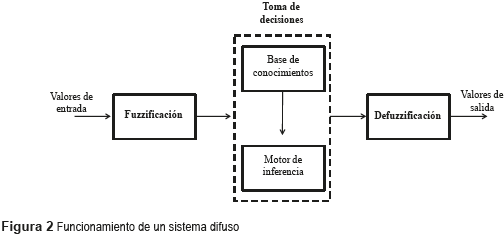
Como se muestra en la figura 2, el funcionamiento de un sistema basado en lógica difusa se fundamenta en tres etapas: fuzzificación, toma de decisiones y defuzzificación de las decisiones tomadas. A continuación se presenta una breve descripción de cada una de las etapas empleadas en un proyecto de control que hace uso de lógica difusa.

Fuzzificación

La primera etapa de un proyecto que utilice la lógica difusa como herramienta de análisis y solución es la denominada fuzzificación. El proceso de fuzzificación puede ser definido como la conversión del conjunto de entradas numéricas en conjuntos difusos. Las operaciones realizadas en la lógica difusa son efectuadas en términos de conjuntos difusos, de esta forma, los datos de entrada deberán expresarse como conjuntos difusos o singletones (elementos unitarios), que son un tipo especial de conjunto difuso. Los valores de entrada necesitan ser designados como valores de pertinencia de uno o más conjuntos difusos en que el universo analizado haya sido dividido. Estos valores de pertinencia son determinados a partir de la intersección del conjunto de datos con los conjuntos difusos del universo seleccionado.

Toma de decisiones

Una vez concluido el proceso de fuzzificación se procede con la siguiente fase del proyecto, esta etapa es conocida como la toma de decisiones. En este paso, un motor de inferencia es empleado con el propósito de determinar los valores de salida del proyecto. Para conseguirlo, el sistema de inferencia se apoya de una base de conocimientos construida a partir de la información disponible del sistema analizado. Esta base de conocimientos está constituida por un banco de datos (funciones de pertinencia) y por un conjunto de reglas que describen el sistema (variables lingüísticas, formato de reglas condicionales, etc.).

Defuzzificación

La etapa final del proceso de aplicación de la lógica difusa consiste en la defuzzificación de las decisiones tomadas. Mediante este procedimiento, es posible reducir el conjunto difuso obtenido al final de la etapa de la toma de decisiones a un singleton. En otras palabras, la defuzzificación es la operación de conversión del conjunto difuso de salida en un valor numérico único. Existen diversos métodos de defuzzificación, siendo los más comunes el método del centroide y el método de la media ponderada de los máximos. En este trabajo, particularmente, se empleó el método del centroide como herramienta de transformación de la salida numérica del proyecto de control propuesto.

El método del centroide es probablemente el procedimiento más utilizado en la defuzzificación de las salidas de un sistema regido por lógica difusa. Este método consiste en determinar el centro de gravedad de la distribución obtenida en el eje de las abscisas. De esta manera, para una distribución continua o discreta se tendrá, respectivamente, las ecuaciones (6) y (7):

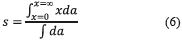
Donde s es el valor numérico de la salida, x y x_i son los valores de las abscisas del punto centroide para la distribución continua y discreta, respectivamente, da y δA_i son los valores de las áreas existentes entre el grado de pertinencia y el eje de las abscisas para cada salida activada.

Modelo numérico empleado

El modelo numérico utilizado en este trabajo es una idealización teórica obtenida a partir de un prototipo experimental, construido en escala real en el laboratorio del Departamento de Estructuras, Geotecnia y Geología aplicada de la Universidad de Basilicata en Italia. Detalles de la obtención de parámetros de dicho modelo numérico pueden ser consultados en [8-11].

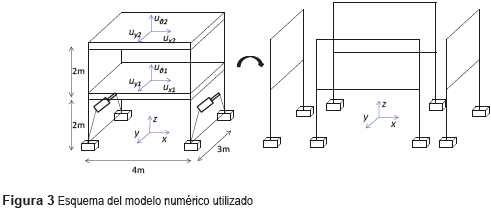
El sistema analizado consiste de un edificio aporticado de dos pisos, con tres grados de libertad por piso (desplazamientos horizontales en los ejes X y Y, y rotación en torno del eje Z). Además, el modelo numérico fue desarrollado teniendo en cuenta el efecto de los mecanismos encargados del control estructural, los cuales son dos amortiguadores MR que se encuentran instalados en la base de la edificación. La figura 3 muestra un esquema del modelo utilizado y su respectiva reducción para la simplificación del análisis.

Los parámetros de masa (M), rigidez (K) y amortiguamiento (C) del modelo son condensados, respectivamente, en las matrices presentadas en (8, 9 y 10). Así:

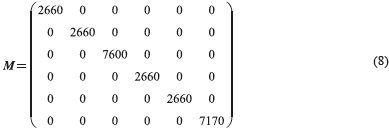
Donde los elementos de masa asociados al desplazamiento tienen unidades de kg y los elementos de masa asociados a la rotación tienen unidades de kg∙m². Ya los elementos de rigidez asociados al desplazamiento y a la rotación tendrán unidades, respectivamente, de N/m y N∙m. Finalmente, los elementos de amortiguamiento asociados al desplazamiento tendrán unidades de N∙s/m, mientras que los elementos de amortiguamiento asociados a la rotación tendrán unidades de N∙s∙m.

Los amortiguadores MR que se utilizaron en el modelo numérico corresponden a disipadores reales referenciados comercialmente como amortiguadores MR RD-1005-3, desarrollados por la empresa Lord Corporation. Para simular numéricamente el comportamiento característico de estos dispositivos, se utilizará el modelo fenomenológico ya descrito en este mismo trabajo.

Con base en ensayos realizados sobre amortiguadores MR RD-1005-3 fue posible determinar los principales parámetros y características mecánicas que definen el desempeño y la conducta del mecanismo disipador [12]. La tabla 1 presenta un resumen con aquellos parámetros constantes obtenidos en el estudio referenciado en [12] y que son necesarios para el modelaje de este amortiguador en particular.

Adicionalmente, se identificó que los parámetros restantes necesarios para la puesta en marcha del modelo fenomenológico eran parámetros variables dependientes del voltaje aplicado en el disipador. Fue entonces determinado que la forma en que estas variables se alteran, corresponde a un comportamiento cercano al descrito en las ecuaciones (11, 12 y 13):

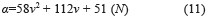
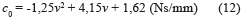
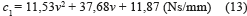
Control semi-activo del modelo utilizando lógica difusa

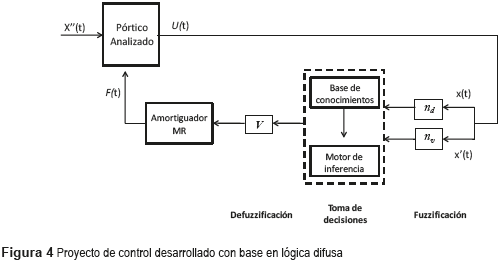
El esquema del proyecto de control difuso propuesto para reducir las vibraciones del pórtico analizado puede ser visto en la figura 4.

Este controlador se basa en las investigaciones desarrolladas en [13, 14]. Con base en estos trabajos, fueron utilizadas como variables de entrada del proyecto de control los valores de desplazamiento y velocidad del primer piso del pórtico objeto de estudio, siendo la variable de salida el valor de voltaje a ser aplicado a los mecanismos de disipación de energía.

El proceso de fuzzificación de los valores de entrada del controlador inicia empleando dos funciones lineales, una para el desplazamiento y la otra para la velocidad, funciones que tienen como objetivo normalizar las respuestas de la estructura en el universo de las funciones de pertinencia definido en el intervalo [-1,1]. Las funciones lineales utilizadas en este trabajo fueron las expresiones (14) y (15):

Donde n_d y n_v son, respectivamente, los valores de entrada normalizados en el universo de las funciones de pertinencia del desplazamiento y de la velocidad, en cuanto k_d y k_v son definidos como factores de escala para el desplazamiento y la velocidad, respectivamente. Basados en análisis de parámetros [13], los factores de escala pueden ser calculados mediante las expresiones (16) y (17):

Donde x_max y 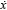_max representan, respectivamente, los valores máximos de desplazamiento y velocidad de la estructura sin control sometida al efecto de una excitación cualquiera. Para determinar los factores de escala de este trabajo, la estructura fue sometida a la acción de un registro de aceleración actuando en la base, cerciorándose de que el registro fuera compatible con las excitaciones que serían utilizadas en el sistema (escalonamiento en el tiempo y en magnitud de acuerdo con las dimensiones de la estructura). Con esto, se determinó que los factores de escala a utilizar deberían ser k_d = 612 y k_v = 20.

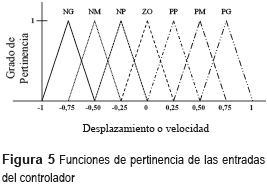
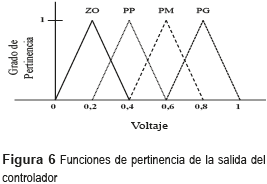
Una vez determinadas las funciones lineales utilizadas para fuzzificar las entradas numéricas del sistema, se pasa a definir las funciones de pertinencia de las entradas y de la salida del controlador. Para el caso específico de las entradas, estas funciones consistirán de siete triángulos idénticos sobrepuestos entre sí en el medio de la base, y definidos a lo largo del universo [-1, 1]. Ya las funciones de pertinencia de la salida del controlador (voltaje) consistirán de cuatro triángulos iguales sobrepuestos entre si también en el medio de la base y definidos para un universo de funciones de pertinencia [0, 1]. Cabe anotar que la definición de las funciones de pertinencia del sistema y sus universos son tomados de [13], siendo éste conjunto de reglas adaptadas al conocimiento heurístico que se tiene del sistema estudiado en este trabajo. Las figuras 5 y 6 presentan, respectivamente, un diagrama de las funciones de pertinencia de las entradas y de la salida del controlador proyectado.

Los valores lingüísticos difusos NG, NM, NP, ZO, PP, PM y PG se refieren, respectivamente, a negativo grande, negativo mediano, negativo pequeño, cero, positivo pequeño, positivo mediano y positivo grande.

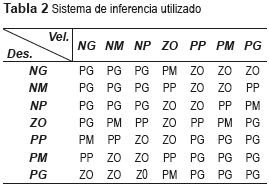
La fase de toma de decisiones será ejecutada con base en un motor de inferencia, que está ligado a una base de conocimientos y que funcionará de acuerdo al grado de pertinencia de las entradas del controlador. El sistema de reglas de inferencia permite calcular el voltaje necesario para que los dispositivos de control disipen eficientemente la energía entrante en la estructura. El sistema se basa en el siguiente principio básico: Si la estructura se encuentra fuera de su posición neutra y la tendencia de su movimiento es la de apartarse aún más de esa posición neutra, entonces el voltaje aplicado debe ser aumentado para incrementar así la capacidad de amortiguamiento. No obstante, si la estructura se encuentra fuera de su posición neutra y la tendencia de su movimiento es la de aproximar el sistema a la posición neutra, entonces poco o ningún voltaje será necesario. La tabla 2 presenta el sistema de inferencia desarrollado en [13] y que fue adaptado para este trabajo.

El grado de pertinencia de la salida del controlador será determinado mediante el método de los mínimos, el cual consiste en seleccionar el grado de pertinencia de salida igual al grado de pertinencia de la entrada menor.

Finalmente, la estrategia de defuzzificación será realizada utilizando el método del centroide, el cual permitirá determinar un valor de voltaje a partir de las áreas sobrepuestas de las funciones de pertinencia de salida. El valor del voltaje obtenido mediante el método del centroide se encuentra en el universo [0, 1], por tanto es necesario utilizar un factor de escala que mapee los valores de salida del universo difuso [0, 1] al universo real [0, 2,5]. El factor de escala utilizado en este trabajo será regido por la expresión (18):

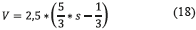
Donde V es el valor de voltaje a aplicar a los dispositivos de control y s es el valor numérico de la salida del método del centroide. El proceso de defuzzificación utilizado en este trabajo fue proyectado de tal forma, que si el valor de voltaje ultrapasa el valor máximo de voltaje permitido en el análisis (2,5 volts), automáticamente se sustituirá el valor determinado en (18) por el valor de voltaje máximo estipulado. Ejemplos numéricos detallados del funcionamiento del controlador difuso aquí presentado pueden ser consultados en [10].

Resultados y discusión

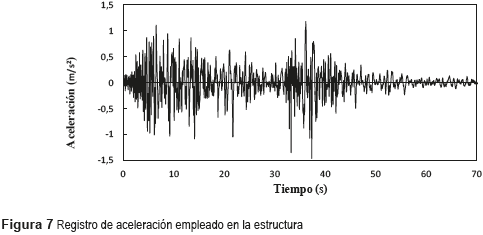
Definidos los principios básicos de funcionamiento del controlador difuso propuesto, se examinará el desempeño de dicho sistema, empleándolo en el pórtico descrito en el modelo numérico. Así, la estructura es sometida en su base a la acción de un registro de aceleración de origen natural y que globalmente reproduce el espectro de suelo tipo B de acuerdo con la norma italiana OPCM3431. Antes, el registro pasó por una preparación inicial, consistente en escalonarle en el tiempo y en magnitud para hacerle compatible con las dimensiones de la estructura. La figura 7 muestra el registro de aceleración utilizado para excitar el sistema estructural analizado.

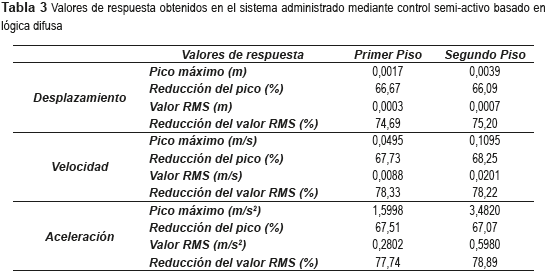
El control mediante lógica difusa se mostró suficientemente apto para disipar la respuesta de la estructura. Para el primer piso, los valores máximos de desplazamiento, velocidad y aceleración fueron, respectivamente, de 0,0017m, 0,0495m/s y 1,5998 m/s², lo que representa reducciones de 66,67%, 67,73% y 67,51% cuando se comparan las respuestas del sistema controlado con las respuestas del sistema sin control. Si son comparados los valores RMS de respuesta del primer piso de la estructura controlada y no controlada, es posible obtener porcentajes de reducción de 74,69%, 78,33% y 77,74% en el desplazamiento, la velocidad y la aceleración, respectivamente.

Los porcentajes de reducción de respuesta del segundo piso de la estructura controlada, no difieren mucho de aquellos obtenidos para el primer piso. Los valores pico de desplazamiento, velocidad y aceleración fueron, respectivamente, de 0,0039m, 0,1095m/s y 3,4820m/s², lo que indica reducciones de 66,09%, 68,25% y 67,07% cuando estos valores son confrontados con los valores del sistema sin control. Por otro lado, los porcentajes de reducción de los valores RMS de la respuesta para el segundo piso del sistema controlado tuvieron valores de reducción de 75,20%, 78,22% y 78,89% en el desplazamiento, la velocidad y la aceleración, respectivamente, si se comparan con los valores del sistema sin control.

La tabla 3 presenta los valores de respuesta máxima y los valores RMS de cada piso de la estructura cuando ésta es sometida a la acción del registro de aceleración mostrado en la Figura 7. En la misma tabla también se presentan los valores de reducción de respuesta en términos de porcentajes, aclarando que los porcentajes de reducción, corresponden a valores calculados mediante la comparación de los valores de respuesta del sistema equipado con control difuso, con los valores de respuesta de la estructura sin control.

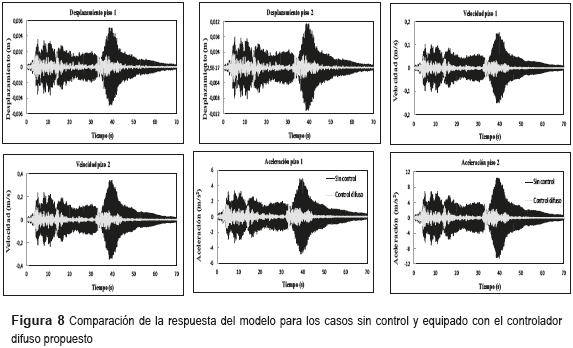
En la figura 8 es posible también examinar el desempeño a lo largo del tiempo del sistema administrado mediante la estrategia de control difuso propuesta. En esta figura se puede observar claramente el historial del sistema controlado comparado con las respuestas del sistema sin control.

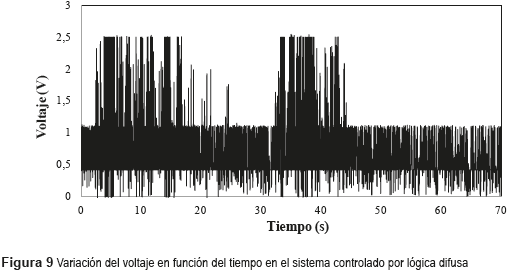
El grafico de variación de voltaje en función del tiempo muestra claramente una franja de tensión en la que el voltaje aplicado a los amortiguadores MR permanece prácticamente constante durante la mayor parte del tiempo del análisis, esta franja de valores se encuentra limitada, aproximadamente, entre los 0,4 y 1,1 volts. Por otro lado, es también posible observar, del mismo gráfico, que el aumento de la señal de comando de los amortiguadores MR es de alguna manera proporcional a la ampliación e intensificación de la excitación actuante en la estructura. La figura 9 presenta la evolución de la tensión a lo largo del tiempo propuesta por el proyecto de control difuso para la administración del sistema estructural sometido a la acción del registro de aceleración mostrado en la figura 7.

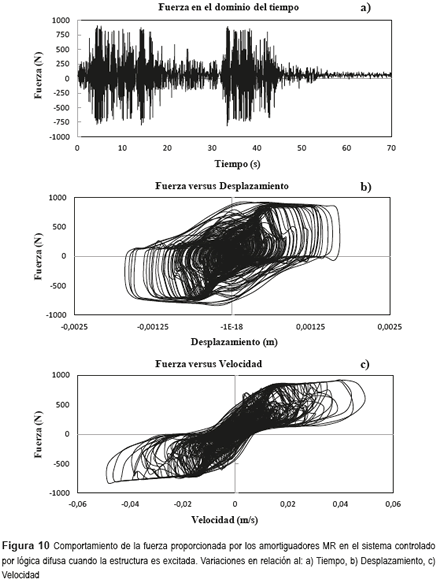
La variación de la tensión a lo largo del tiempo generada por el algoritmo de control difuso propuesto, genera en los amortiguadores MR una fuerza de control que actuará en la estructura, reduciendo de esta forma los valores de respuesta del pórtico cuando éste es excitado. La figura 10 presenta la evolución de la fuerza de control desarrollada por el conjunto controlador-amortiguador, para este caso particular, en relación al tiempo, desplazamiento y velocidad. De esta figura es destacable el comportamiento poco convencional del grafico ''Fuerza versus Desplazamiento'', el cual presenta una forma distorsionada de la representación comúnmente obtenida en este tipo de controladores semi-activos, esto debido probablemente a variaciones rápidas y bruscas del voltaje propias de las decisiones tomadas por el algoritmo de control difuso propuesto y que no son tan comunes en otros algoritmos de control utilizados comúnmente en amortiguadores MR.

Conclusiones

El proyecto de control estructural fundamentado en lógica difusa propuesto en este artículo muestra la valía de los algoritmos de control basados en el conocimiento heurístico que se tenga del problema abordado, equiparando de alguna forma el desempeño de algoritmos altamente sofisticados y complejos que logran reducciones de valores de respuesta importantes, pero que requieren de alto poder de procesamiento.

A partir del ejemplo numérico desarrollado fue posible observar que el controlador trabajado alcanzó reducciones en los picos de los valores de respuesta de la estructura estudiada de hasta 68%, en cuanto la reducción de los valores de respuesta RMS de los dos niveles del pórtico analizado eran reducidos hasta en un 78%, valores significativos en los que se demuestra disminuciones mayores a 2/3 de las amplitudes de movimiento del sistema, lo que necesariamente lleva a pensar en una mejor reacción por parte de la estructura ante eventualidades ambientales de carácter transitorias.

De esta forma, es posible concluir que la estrategia de administración de fuerzas de control se mostró bastante equilibrada, pues combina claramente una notable eficiencia junto con rapidez de procesamiento y simplicidad. En un potencial caso práctico, el controlador basado en conjuntos difusos planteado podría ser implementado fácilmente a partir de un estudio riguroso de las principales características y propiedades del sistema estructural que se pretenda administrar.

Agradecimientos

Los autores agradecen el apoyo brindado por la Universidad Nacional de Colombia sede Medellin, la Universidad de Brasilia y el CNPq para el desarrollo de este trabajo.

Referencias

1.  G. Yang. Large-Scale Magnetorheological Fluid Damper for Vibration Mitigation: Modeling, Testing and Control. Ph.D. Dissertation, University of Notre Dame. Indiana, USA. 2001. pp. 1-480.         [ Links ]

2.  J. Rabinow. ''The magnetic fluid clutch''. AIEE Transactions. Vol. 67. 1948. pp. 1308-1315.         [ Links ]

3.  J. Rabinow. Magnetic fluid torque and force transmitting device. U.S. Patent 2575360. 1951.         [ Links ]

4.  S. Dyke. Acceleration feedback control strategies for active and semi-active control systems: modeling, algorithm development, and experimental verification. Ph.D. Dissertation, University of Notre Dame. Indiana, USA. 1996. pp. 255.         [ Links ]

5.  B. Spencer, S. Dyke, M. Sain, J. Carlson. ''Phenomenological model of a magnetorheological damper''. Journal of engineering mechanics. Vol. 123. 1997. pp. 230-238.         [ Links ]

6.  G. Chen, T. Pham. Introduction to fuzzy sets, fuzzy logic and fuzzy control systems. 1^st ed. Ed. CRC Press. Florida, USA. 2001. pp. 316.         [ Links ]

7.  R. Tanscheit, E. Sharf. Controle de um braço mecânico através de um controlador nebuloso self-organizing. Proceedings of the 8^th Anais Congresso Brasileiro de Automática. Pará, Brazil. 1990. pp. 481-487.         [ Links ]

8.  R. Carneiro. Controle semi-ativo de vibrações em estruturas utilizando amortecedor magnetoreológico. Doctoral Thesis, Universidade de Brasília. Brasília, Brazil. 2009. pp. 135.         [ Links ]

9.  A. Contento, V. Gattulli, M. Lepidi, F. Potenza. Identificazione di modelli per un protótipo sperimentale di telaio tridimensionale com controventi semi-attivi. Report DISAT-UOIS N.° 2. L'Aquila, Italy. 2006. pp. 33.         [ Links ]

10.  L. Lara. Estudo de algoritmos de controle semi-ativo aplicados a amortecedores magnetoreológicos. Doctoral Thesis, Universidade de Brasília. Brasília, Brazil. 2011. pp. 223.         [ Links ]

11.  L. Lara, J. Brito, Y. Valencia. ''Reducción de vibraciones en un edificio mediante la utilización de amortiguadores magnetoreológicos''. DYNA. Vol. 171. 2012. pp. 205-214.         [ Links ]

12.  M. Basili. Controllo semi attivo di strutture adiacenti mediante dispositivi magnetoreologici: teoria, sperimentazione e modellazione. Doctoral Thesis, Università degli studi di Roma ''La Sapienza''. Rome, Italy. 2006.         [ Links ]

13.  Y. Liu, F. Gordaninejad, C. Evrensel, G. Hitchcock. ''An Experimental Study on Fuzzy Logic Vibration Control of a Bridge Using Fail-Safe Magneto-Rheological Fluid Dampers''. SPIE - The International Society for Optical Engineering. Vol. 4330. 2001. pp. 281-288.         [ Links ]

14.  C. Dias. Fuzzy Control of Magnetorheological Dampers for Vibration Reduction of Seismically Excited Structures. Ph.D. Dissertation, Florida State University. Tallahassee. Florida, USA. 2005. pp. 1-454.         [ Links ]