Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.75 Medellín abr./jun. 2015
https://doi.org/10.17533/udea.redin.n75a20
ARTÍCULO ORIGINAL
DOI: 10.17533/udea.redin.n75a20
Robust tracking control for linear vibrating mechanical systems
Control de seguimiento robusto para sistemas mecánicos vibratorios lineales
Francisco Beltrán-Carbajal*
Departamento de Energía, Unidad Azcapotzalco, Universidad Autónoma Metropolitana. Av. San Pablo N.° 180, Colonia Reynosa Tamaulipas. México D.F., México.
* Corresponding author: Francisco Beltrán Carbajal, e-mail: fbeltran.git@gmail.com
DOI: 10.17533/udea.redin.n75a20
(Received March 01, 2015; accepted April 20, 2015)
Abstract
A novel output feedback tracking control approach is proposed for underactuated linear mass-spring-damper vibrating mechanical systems of multiple degrees of freedom. The presented control design methodology considers robustness against unmodeled dynamics and external forces. The proposed control scheme only requires measurements of the position output variable. Tracking error integral compensation is properly used to avoid real-time disturbance estimation. Analytical and numerical results prove the effectiveness of the introduced active vibration control scheme for resonant and chaotic vibration attenuation on the output variable response.
Keywords: mechanical vibration systems, mass-spring-damper systems, multiple degrees-of-freedom mechanical systems, active vibration control
Resumen
Se propone un enfoque de control novedoso para seguimiento por realimentación de la salida para sistemas mecánicos vibratorios del tipo masa-resorte-amortiguador lineales sub-actuados. La metodología de diseño de control que se presenta considera robustez con respecto de dinámicas no modeladas y fuerzas externas. El esquema de control propuesto solamente requiere mediciones de la variable de la salida de posición. Se utiliza compensación integral del error de seguimiento de manera apropiada para evitar la estimación en tiempo real de las perturbaciones. Resultados analíticos y numéricos muestran la efectividad del esquema de control activo de vibración para atenuación de vibraciones resonantes y caóticas afectando la respuesta de la variable de salida.
Palabras clave: sistemas mecánicos vibratorios, sistemas masa-resorte-amortiguador, sistemas mecánicos de múltiples grados de libertad, control activo de vibraciones
Introduction
Active vibration control design for complex vibrating mechanical systems of multiple degrees of freedom is commonly based on reduced order models. Moreover, weakly damped flexible mechanical structures can be perturbed by completely unknown resonant excitation forces during their operation; as a consequence, undesirable forced vibrations are amplified. This problem becomes quite defiant for practical applications where the available number of sensors and actuators is much less than the number of degrees of freedom of the flexible structure to be controlled.
Thus, output feedback control of dynamical systems subjected to endogenous and exogenous disturbances represents a long standing challenging research topic. In this regard, active disturbance rejection control has been recently proposed to deal with these issues [1, 2]. Here, disturbances are estimated and compensated by the controller in real time. In [3], disturbance rejection has been also addressed from a model-free control perspective, introducing recently the algebraic design methodology of intelligent Proportional-Integral-Derivative controllers (iPIDs), where an unknown mathematical model is replaced by an ultra-local model.
This paper deals with efficient and robust tracking control in underactuated linear mass-spring-damper systems with multiple degrees of freedom without on-line disturbance estimation. A wide variety of vibrating mechanical engineering systems can be represented by mass-spring-damper models. Some practical application examples of mass-spring-damper systems can be found in dynamic vibration absorbers [4-7], balancing of rotating machinery [8-10], metal-cutting machine tools [11, 12], vehicle suspension systems [13] and other real engineering systems (see, e.g., [14-16]). Thence, efficient control of mass-spring-damper systems is a high relevance research topic in practical engineering systems.
In previous works, it has been shown theoretically and experimentally the potential application of the Generalized Proportional-Integral (GPI) control design methodology for robust perturbation rejection in a mass-spring-damper mechanical system of one degree of freedom [17] and in the synthesis of active vibration absorption schemes to attenuate undesirable harmonic vibrations [18]. GPI control and integral reconstructors of the state variables for constant linear systems were introduced in [19] to avoid the use of asymptotic state observers. Thus, GPI control represents a good alternative for active control of controllable mechanical systems using only measurements of the output variables.
In this paper, a novel output feedback dynamic control scheme is proposed for robust reference position trajectory tracking tasks in perturbed underactuated linear mass-spring-damper system with multiple degrees of freedom. It is shown that the mechanical system exhibits the differential flatness property [20], which is advantageous exploited in our study. A simplified mathematical model of the transformed differentially flat mechanical system is used for control design purposes. Unmodeled dynamics and external forces are lumped in a state-dependent perturbation affecting the known system dynamics. The perturbation signal is locally approximated by a family of certain order Taylor polynomials into a small time window. Then, GPI control, differential flatness and Taylor polynomial expansion of the perturbation signal are properly combined for the synthesis of the presented control scheme, which only requires measurements of the system position output variable.
A challenging simulation case study was purposely selected to evaluate the dynamic performance of the proposed control approach, showing satisfactory results. Robustness is considered with respect to unmodeled dynamics, resonant excitation forces and chaotic disturbances generated by an uncertain symmetric gyro with linear-plus-cubic damping subjected to harmonic excitation as well [21].
Multiple degrees-of-freedom mass-spring-damper system
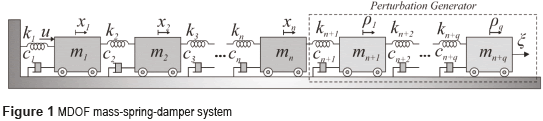
Consider the Multiple - Degrees-Of-Freedom (MDOF) vibrating mechanical system schematically represented in Figure 1. The vibration system consists of a completely controllable state main system (Σ1) and an uncertain dynamic perturbation generator system (Σ2) subjected to unknown time varying bounded disturbances ξ(t), possibly generated by another dynamic system as well. The generalized coordinates are the positions of the mass carriages, xi and ρj, i = 1, 2, ..., n, j = 1, 2, ..., q. In addition, u is a single force control input for regulation and trajectory-tracking tasks on the mechanical system, and y=xn represents the position output variable to be controlled. mi, ki and ci denote mass, stiffness and viscous damping associated to the i-th degree-of-freedom.
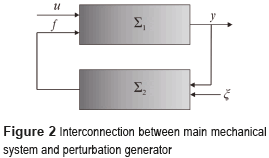
The vibration mechanical system can also be represented by the feedback energetic interconnection of Figure 2. Here, the main mechanical system and the perturbation generator are modeled by Σ1 and Σ2, respectively, where f is the induced disturbance force affecting the main system. Notice that the main system resembles a highly perturbed underactuated MDOF system with a single input (u) and a single output (y). The mathematical model of the mechanical system is described by the coupled ordinary differential Eqs. (1) and (2).
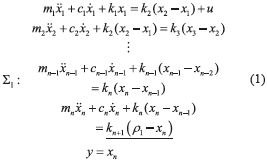
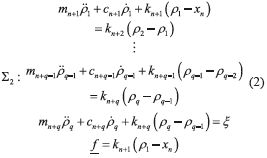
The augmented system given by (1) and (2) is stable in the case of u ≡ 0 and ξ ≡ 0. Indeed, defining the storage function (3) as the total energy of the system, with x0 = 0 and ρ0 = xn.
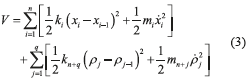
And taking the time derivative of V along the system trajectories results in the expression (4).
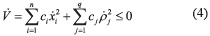
Then 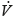 ≡ 0 if and only if
≡ 0 if and only if 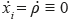 , and hence xi = ρj ≡ 0. Therefore, from the LaSalle's Theorem [22] is proved that the augmented system (1) and (2) is globally asymptotically stable. In addition, as a consequence, it is widely known that for any bounded (control or disturbance) input signals, the state variables will also remain bounded (see, e.g., [23]).
, and hence xi = ρj ≡ 0. Therefore, from the LaSalle's Theorem [22] is proved that the augmented system (1) and (2) is globally asymptotically stable. In addition, as a consequence, it is widely known that for any bounded (control or disturbance) input signals, the state variables will also remain bounded (see, e.g., [23]).
A robust output feedback tracking control scheme
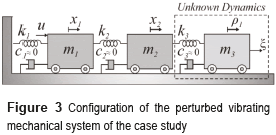
Firstly, we consider that, without any loss of generality and for simplicity, the dynamics associated to the first two masses is only known. Therefore, the two degree-of-freedom underactuated mechanical system is perturbed by the unknown force (5).

Notice that the force f is, strictly speaking, a time-varying disturbance depending on the unknown dynamics of the perturbation generator system coupled to the second mass m2 through the spring k3.
Moreover, the equilibrium points of the properly controlled dynamical system (1) and control input parameterized in terms of the desired output position 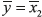 are given by (6), where the notation (
are given by (6), where the notation (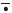 ) is used to denote stable equilibrium operation condition.
) is used to denote stable equilibrium operation condition.

Let z1 = x1, z2 = x1, z3 = x2, z4 = 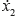 , we have the state space description (7).
, we have the state space description (7).
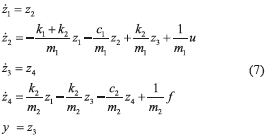
The known mass-spring-damper system dynamics (7) exhibits the differential flatness property and, hence, the controllability property as well [20]. Therefore all state variables and the control input can be parameterized in terms of the flat output y and a finite number of its time derivatives. For this, the time derivatives up to fourth order for y are obtained as (8).
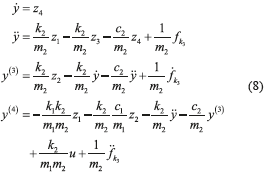
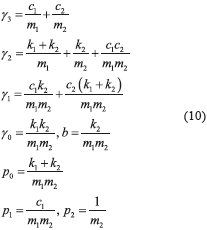
Therefore the differential parameterization results in (9) with positive constants (10).
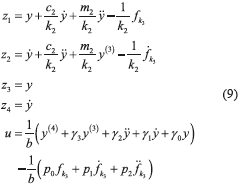
The flat output y then satisfies the perturbed input-output differential Eq. (11).
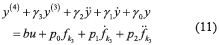
Thus, the structural property of differential flatness can be conveniently used to design an output feedback dynamic control scheme for reference trajectory tracking tasks for the output position variable y and, consequently, all trajectories of the dynamical system as described by (9).
The perturbed input-output mathematical model (11) can also be rewritten in the form (12), where we assume that the position output variable y is the only available measurement signal for the synthesis of some tracking control scheme. Evidently, this assumption is established in order to reduce control implementation costs.
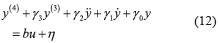
where η is a completely unknown disturbance signal affecting the dynamics of the output variable y, which is given by (13).
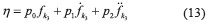
Note that, one can additionally consider small parametric uncertainties into the disturbance signal η.
It is assumed that the bounded disturbance signal η can be approximately reconstructed into a sufficiently short time interval by a family of Taylor polynomials of r th degree as (14) around a given time instant t0 ≥ 0 [5, 17].
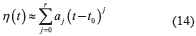
where coefficients aj are completely unknown, and residual terms of the truncated Taylor expansion are negligible if t↓t0 or r→∞.
Note that, one could simply choose a (straight line) first order truncated Taylor polynomial function to get an approximation of a time-varying signal into a quite small time window. Nevertheless, a Taylor polynomial family of higher order will allow to get a better reconstruction of some signal into a short period of time, say, (t0,t0+ε), where ε is a positive and sufficiently small value.
Hence, by using the polynomial approximation (14) for the signal η, the dynamics of the mechanical system can be locally described as (15).
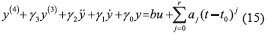
From Eq. (15), one can then obtain, by successive integrations with respect to time, the structural estimates (16) for the time derivatives up to third order of the flat output y [19]. Here the notation ''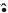 '' is used to represent derivative estimates.
'' is used to represent derivative estimates.
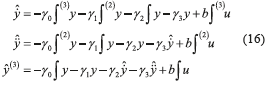
For simplicity, the integral 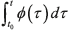 is described by
is described by 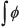 and
and 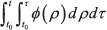 by
by 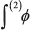 , and so on.
, and so on.
In the integral reconstruction of the time derivatives of the position output signal, the system initial conditions and the coefficients aj were intentionally ignored. Therefore, the structural estimates (16) differ from the actual values by an algebraic polynomial up to (r+3)th degree of the form (17).
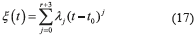
where constants λj depend on the unknown initial conditions at t0 ≥ 0 and the coefficients of the disturbance model (14).
The robust output feedback tracking dynamic controller (18) using integral reconstruction of the time derivatives (16) is then proposed.
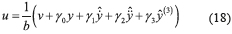
The auxiliary control input v given by expression (19) is synthesized to get the desired asymptotic output tracking of the reference position trajectory y*(t) specified for the mechanical system.
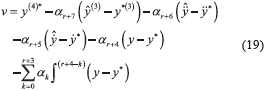
The last integral error compensation terms are used to actively reject disturbances due to estimation errors, unmodeled dynamics and parametric uncertainty.
Substitution of the controller (18) into system (15), and differentiating r+4 times the resulting expression with respect to time, results in the closed loop dynamics of the tracking error (20), e = y – y*.
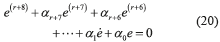
The characteristic polynomial associated with the closed loop tracking error dynamics (20) is then given by (21).
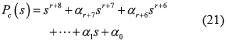
Therefore, the control gains αj, j = 0, 1, 2, ..., r+7, are selected so that the characteristic polynomial (21) is a Hurwitz polynomial, sufficiently far from the imaginary axis in the left half of the complex plane, faster than the highest excitation frequencies present in disturbances. In this way, the asymptotic tracking of the desired reference position trajectory y*(t) can then be verified. Since the characteristic polynomial (21) does not depend of the coefficients aj of the polynomial expansion of the disturbance signal (14) and the constants λj of the derivatives reconstruction error polynomial (17), the control scheme (19) continually self-updates for any operation time interval of the mechanical system. Notice that under the assumption of a small residual term of the truncated Taylor polynomial expansion of the disturbance signal η in the vicinity of the current time t, the tracking error dynamics represents an asymptotically exponentially stable system perturbed by a uniformly bounded signal of very small amplitude. Therefore, the tracking error remains uniformly bounded by a small radius disk centered at the origin [23].
Finally, we now consider the tracking control problem for the n DOF linear vibrating mechanical system using a single control input u applied to the first mass m1. Since the vibrating mechanical system (1) is a differentially flat dynamical system, we get the disturbed input-output transformed system dynamics (22), where yn denotes the available output position variable of the mass mn to be used in the controller synthesis. Again, η represents the disturbances affecting the known system dynamics.
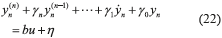
Hence, by following the control design methodology described above, we propose the output feedback tracking dynamic control scheme (23) for asymptotic reference trajectory tracking tasks, yn(t), for n DOF linear vibrating mechanical systems.
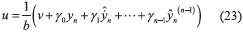
Where the auxiliary control input v is now given by Eq. (24).
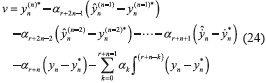
One can likewise get, by successive integrations of Eq. (22), integral recontructors 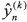 , k = 1, 2,…, n-1, for the time derivatives of the flat output yn.
, k = 1, 2,…, n-1, for the time derivatives of the flat output yn.
The closed loop dynamics of the tracking error, e=yn–y*, is thus described by Eq. (25).
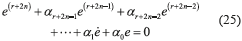
Hence, the asymptotic tracking of the desired reference trajectory y*n(t) can be accomplished by the proper selection of the control gains αj, j = 0, 1, 2, ..., r+2n – 1 as it is stated above.
A study case: simulation results
The robust and efficient performance of the proposed control approach was verified for the weakly damping vibrating mechanical system shown in Figure 3. Our case study considers unmodeled dynamics associated with the unknown secondary mechanical system (m3, c3, k3) perturbed as well. The mechanical system of three degrees of freedom is characterized by the set of parameters given in Table 1. Then, the natural frequencies of the mechanical system are computed as: ωn1 = 6.6854 rad/s, ωn2=17.361 rad/s and ωn3=35.174 rad/s.
Moreover, resonant and chaotic dynamical disturbance forces ξ described by (26) were purposely taken into account in the robustness assessment. Evidently, this situation is the worst operation scenario for any vibrating mechanical system.
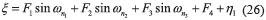
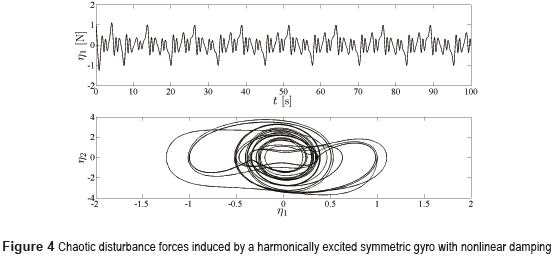
The perturbation force amplitudes are: F1=0.5 N, F2=0.25 N, F3=0.3 N and F4=4 N. The chaotic force term η1 is generated by a symmetric gyro shaker with linear-plus-cubic damping given by (27), which is also subjected to harmonic excitation [21]. The parameter values of this highly nonlinear dynamical system are: α2=100, β=1, b1=0.5, b2=0.05, ω = 2 and g=36, with initial conditions: η1(0)=1, η2(0)=0.2. Figure 4 depicts the time response and phase trajectory of the perturbation force generator exhibiting both regular and chaotic dynamics (motions).
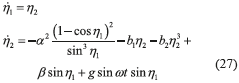
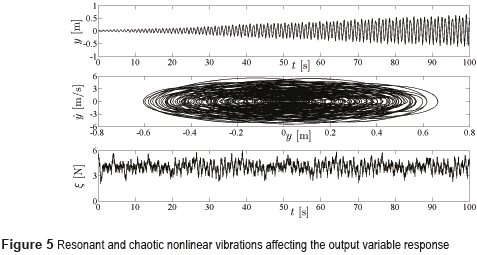
Figure 5 shows the presence of large nonlinear vibrations when the mechanical system is subjected to resonant and chaotic disturbance forces ξ and operated without active vibration control (u≡0). Certainly, these vibration levels are prohibited, and the active vibration control should hence supress undesirable vibrations below acceptable vibration attenuation levels.
On the other hand, the active vibration control scheme (23) was specified to suppress vibrations and simultaneously achieve robust tracking of the reference trajectory y*(t) on the position output variable, y=x2. The motion profile y*(t) planned for the mechanical system is described by (28).
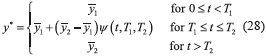
where  1= 0 m,
1= 0 m, 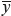 2=0.01 m, T1=5 s, T2=10 s, and ψ(t, T1,T2) is a Bézier polynomial, with ψ(T1, T1,T2)=0 and ψ(T2, T1,T2)=1, given by (23).
2=0.01 m, T1=5 s, T2=10 s, and ψ(t, T1,T2) is a Bézier polynomial, with ψ(T1, T1,T2)=0 and ψ(T2, T1,T2)=1, given by (23).
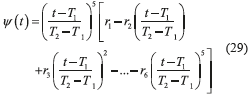
with r1=252, r2=1050, r3=1800, r4=1575, r5=700, r6=126.
The disturbance signal η(t) was locally approximated by a family of Taylor polynomials of fourth degree. Thus, the design parameters for the controller were selected to have a twelfth order closed-loop characteristic polynomial of the form (30).
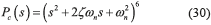
with natural frequency ωn=100 rad/s and damping ratio ζ=0.7071.
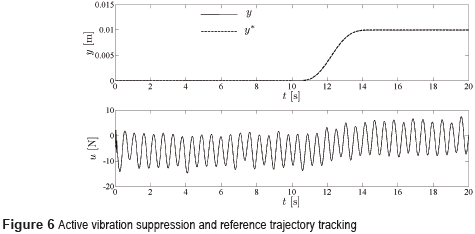
Figure 6 manifests the robust and efficient performance of the proposed output feedback control scheme. The vibration suppression and satisfactory tracking of the reference position trajectory are clearly verified. Therefore, the presented design methodology represents a good alternative for the controller synthesis for underactuated perturbed linear mass-spring-damper mechanical systems employing measurements of the single position output variable only.
Conclusions
In this paper, a novel output feedback dynamic control scheme has been proposed for robust reference position trajectory tracking tasks for underactuated linear MDOF mass-spring-damper mechanical systems subjected to disturbances due to un-modeled dynamics and exogenous forces. The state dependent disturbances are induced by couplings of the system with another unknown mass-spring-damper system. The perturbation signal was locally approximated by a family of Taylor polynomials of certain degree in order to reduce the complexity of the controller design. Then, GPI control, differential flatness and the Taylor polynomial expansion of the perturbation signal were properly combined for the synthesis of the presented control scheme. An important feature of the control scheme is its capability of rejecting disturbances using only measurements of the position output variable and simultaneously to perform the motion planning specified for the mechanical system. The robust performance of the control scheme was verified for resonant vibration suppression and active rejection of chaotic disturbances generated by an uncertain symmetric gyro with linear-plus-cubic damping perturbed by harmonic excitation as well, showing satisfactory results. Therefore, the presented control approach represents a good alternative for the controller synthesis for underactuated perturbed linear mass-spring-damper systems.
References
1. J. Han. ''From PID to Active Disturbance Rejection Control''. IEEE Transaction on Industrial Electronics. Vol. 56. 2009. pp. 900-906. [ Links ]
2. Z. Gao. Active Disturbance Rejection Control: A Paradigm Shift in Feedback Control System Design. Proceedings of the American Control Conference. Minneapolis, USA. 2006. pp. 2399-2405. [ Links ]
3. M. Fliess, C. Join. ''Model-free control''. International Journal of Control. Vol. 86. 2013. pp. 2228-2252. [ Links ]
4. B. Korenev, L. Reznikov. Dynamic Vibration Absorbers. 1st ed. Ed. John Wiley & Sons. Chichester, England. 1993. pp. 1-296. [ Links ]
5. F. Beltrán. ''Variable frequency harmonic vibration suppression using active vibration absorption''. Rev. Fac. Ing. Univ. Ant. N.º 73. 2014. pp. 144-156. [ Links ]
6. F. Beltrán, G. Silva. ''Adaptive-Like Vibration Control in Mechanical Systems with Unknown Parameters and Signals''. Asian J. Control. Vol. 15. 2013. pp. 1613-1626. [ Links ]
7. F. Beltrán, G. Silva. ''Active Vibration Control in Duffing Mechanical Systems Using Dynamic Vibration Absorbers''. Journal of Sound and Vibration. Vol. 333. 2014. pp. 3019-3030. [ Links ]
8. S. Zhou, J. Shi. ''Active balancing and vibration control of rotating machinery: a survey''. Shock and Vibration Digest. Vol. 33. 2001. pp. 361-371. [ Links ]
9. J. Vance, F. Zeidan, B. Murphy. Machinery Vibratin and Rotordynamics. 1st ed. Ed. John Wiley & Sons. New Jersey, USA. 2010. pp. 71-114. [ Links ]
10. F. Beltrán, G. Silva, M. Arias. ''Active Unbalance Control of Rotor Systems Using On-Line Algebraic Identification Methods''. Asian J. Control. Vol. 15. 2013. pp. 1627-1637. [ Links ]
11. K. Byung, R. Seung, P. Jong. ''Development of a 3-axis desktop milling machine and a CNC system using advanced modern control algorithms''. International Journal of Precision Engineering and Manufacturing. Vol. 11. 2010. pp. 39-47. [ Links ]
12. F. Beltrán, E. Chavez, A. Favela, R. Vazquez. ''Active Perturbation Rejection in Motion Control of Milling Machine Tools''. Rev. Fac. Ing. Univ. Ant. N.° 69. 2013. pp. 193-204. [ Links ]
13. E. Chavez, F. Beltrán, A. Valderrabano, A. Favela. ''Active Vibration Control of Vehicle Suspension Systems Using Sliding Modes, Differential Flatness and Generalized Proportional-Integral Control''. Rev. Fac. Ing. Univ. Ant. N.° 61. 2011. pp. 104-113. [ Links ]
14. S. Rao. Mechanical Vibrations. 5th ed. Ed. Prentice Hall. New Jersey, USA. 2011. pp. 10-13. [ Links ]
15. S. Braun, D. Ewins, S. Rao. Encyclopedia of Vibration. 1sted. Ed. Academic Press. London, UK. 2002. pp. 1-26. [ Links ]
16. A. Piersol, T. Paez. Harris's Shock and Vibration Handbook. 6th ed. Ed. McGraw-Hill. Columbus, USA. 2010. pp. 6.1-6.33. [ Links ]
17. H. Sira, F. Beltrán, A. Blanco. ''A Generalized Proportional Integral Output Feedback Controller for the Robust Perturbation Rejection in a Mechanical System''. Sciences et Technologies de l'Automatique. Vol. 5. 2008. pp. 24-32. [ Links ]
18. F. Beltrán, G. Silva, H. Sira. Active Vibration Absorbers Using Generalized PI and Sliding-Mode Control Techniques. Proceedings of the American Control Conference. Denver, USA. 2003. pp. 791-796. [ Links ]
19. M. Fliess, R. Marquez, E. Delaleau, H. Sira. ''Correcteurs Proportionnels-IntégrauxGénéralisés''. ESAIM: Control, Optimization and Calculus of Variations. Vol. 7. 2002. pp. 23-41. [ Links ]
20. M. Fliess, J. Lévine, P. Martin, P. Rouchon. ''Flatness and defect of nonlinear systems: introductory theory and examples''. International Journal of Control. Vol. 61. 1995. pp. 1327-1361. [ Links ]
21. H. Chen. ''Chaos and chaos synchronization of a symmetric gyro with linear-plus-cubic damping''. Journal of Sound and Vibration. Vol. 255. 2002. pp. 719-740. [ Links ]
22. H. Khalil. Nonlinear Systems. 3rd ed. Ed. Prentice Hall. New Jersey, USA. 2002. pp. 126-130. [ Links ]
23. W. Rugh. Linear System Theory. 2nd ed. Ed. Prentice Hall. New Jersey, USA. 1996. pp. 203-216. [ Links ]