Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.76 Medellín July/Sept. 2015
https://doi.org/10.17533/udea.redin.n76a03
ARTÍCULO ORIGINAL
DOI: 10.17533/udea.redin.n76a03
Fuzzy logic controller to cooperative mobile robotics Implemented in leader-follower formation Approach
Controlador de lógica difusa para robótica cooperativa móvil implementando el método líder-seguidor
Manuel Alejandro Molina-Villa*, Daniel Ricardo Avendaño-Flórez, Leonardo Enrique Solaque-Guzmán, Nelson Fernando Velasco-Toledo
Grupo de investigación en Desarrollo de Aplicaciones Mecatrónicas (GIDAM), Facultad de Ingeniería, Universidad Militar Nueva Granada. Carrera 11 n.o 101-80. C. P. 110111. Bogotá, Colombia.
* Corresponding author: Manuel Alejandro Molina Villa, e-mail: mmolina2127@hotmail.com
DOI: 10.17533/udea.redin.n76a03
(Received December 03, 2014; accepted April 29, 2015)
ABSTRACT
This paper presents the design of a fuzzy logic cooperative control by implementing the leader-follower approach that allows establishing and maintaining a specific geometric formation to a mobile robot group while they are moving along a predefined trajectory. As a result of the research, it was proved by simulation, a cooperative control system that permits a set of robots to keep a specific formation while the group performs a predetermined mission. This control system helps avoid obstacles by modifying the formation or by changing the leader inside the group.
keywords: Control systems, cooperative robotics, mobile robotics, fuzzy logic control, leader-follower
RESUMEN
Este artículo presenta el diseño de un controlador de lógica difusa implementando el método líder-seguidor para un sistema de robótica cooperativa móvil, que permita a un grupo de robots establecer y mantener una formación geométrica especifica mientras se desplazan siguiendo una trayectoria de referencia. Como resultado de la investigación, se probó mediante simulación un sistema de control cooperativo, que permite a un grupo de robots mantener una formación específica mientras desarrollan una misión determinada. Este controlador permite evadir obstáculos cambiando la formación o cambiando el líder del grupo en cualquier momento.
palabras clave: Sistema de control, robótica cooperativa, robótica móvil, controlador de lógica difusa, líder-seguidor
1. Introduction
Currently, the research in robotics has extended its interest to multi-robot systems trying to make easier the robots implementation in real applications that could help the society. Certainly, this kind of systems could develop several complex applications more economically and efficiently than a single-robot system. The construction of a multi-robot system has another advantage; the robots that are implemented are simpler, cheaper and more flexible than a single powerful robot developing a specific task [1].
The main idea of the cooperative mobile robotics is that one group of mobile robots can develop the same task better than a single robot, if they work coordinately. Controlling the position of each robot while they are moving in group, is the main problem of the formation control. However, if the group works cooperatively, each robot can take advantage sharing sensor signals; as a consequence, they save resources and have better fault-tolerance. This kind of robotics is introduced in applications such as smart assistive environments or security; but its current main interest is to maintain a specific formation when the group is moving. Three main solutions are used to solve this problem, the leader-follower, virtual structure and behavior-based approaches [2], they are used for introducing the cooperative robotics in many applications for instance, search and rescue missions [3], automated highway systems [4], and robot soccer.
The virtual structure approach takes the total group formation as a single rigid structure, because this method is based on the arrangement around virtual points. In this approach, all robots work as a single complex robot that can move and rotate. This approach is used in applications where the trajectory and the formation are the same all time, but it is not appropriate if the application requires a decentralized system [5].
On the other hand, in behavior-based approach, each robot has a specific task but the interaction between them generates global desirable behaviors. Such specific task could be, for example, avoiding obstacles and collisions, seeking a goal or keep the formation. The task to be developed by each robot is determined, depending on the weighted sum of the basic behaviors that denotes the relative importance of each behavior. Then, the efficiency of this complex approach cannot be easily determined posing the main disadvantage of this method [5].
In the leader-follower approach, the problem is divided into two different roles. One robot is denominated the leader of the group and others are identified as followers. In this method, the leader is the unique robot that knows the reference trajectory [6] and its responsibility is to guide the group to follow the reference, but the followers' responsibility is to maintain the formation respect to the leader [7]. This is the most common technique used in research, because the formation control practically is converted into two simple problems, a trajectory tracking by the leader and a control to keep the formation by the followers [8-10]. Furthermore, this method simplifies the programming and is more efficient computationally than the other two techniques, but its drawback is that the group must have a full-time communication, to send the leader's position to all the followers and if it does not exist a feedback from the leader, the formation could be broken [11, 12].
The main contribution of this paper is to develop a fuzzy logic control for a wheeled mobile robot group, which establishes and maintains a geometrical formation, during the route to the goal using the Leader-follower approach. Other contribution is the implementation of the fuzzy logic to design a control system that permits the group to change different aspects as the role, the pattern formation or the reference of each robot while the mission is being developed, giving different methods to avoid obstacles and resolve the noise problems.
The mobile robots present a lot of perturbations because they are in a really noisy environment, and all those disturbances are a big problem for the movement of the robots. An example of noise source to solve by the controller is the communication delay between the robots. The fuzzy logic control has had good results solving this kind of problem as in [3], and fuzzy logic is well implemented in this kind of robotics because it is the simplest way to develop it [13].
2. Formation control
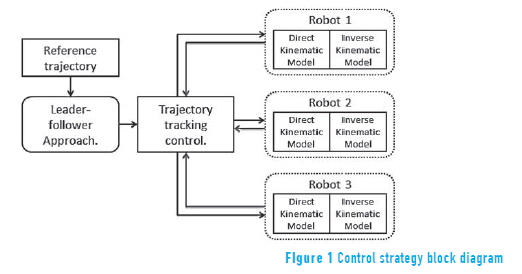
In order to solve the formation control problem for a group of mobile robots, it is necessary to implement two independent controllers (see Figure 1). The objective of the first one is to maintain each robot inside the group formation. On the other hand, the second one is divided in two parts: an individual controller implemented in each robot and a trajectory tracking control that guides the robot to follow the instruction that the group controller sends. The last controller is developed depending on each mobile robot configuration. This article focuses primarily on the design of the trajectory generation control, based in the leader-follower approach using a fuzzy logic controller.
To develop the group controller, the leader-follower approach is the best solution, considering that it generates all trajectories that each robot has to follow. This controller must guide each robot to converge into a desired geometrical formation and maintain it while the group is moving along a trajectory. To achieve this goal, the controller receives the reference trajectory and its responsibility is to generate the linear velocities that each mobile robot should have to maintain the formation [14]. The reference trajectory is associated to inertial coordinate system and it can be implemented in any robot that moves on the plane (X, Y), and is defined as follows in the Eq. (1), where Tx and Ty represent the axes position respectively:
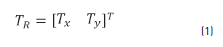
3. Mobile robot modeling
To develop a group controller that can be used in any type of mobile robot, the system is modeled as a simple particle that moves in the plane (X, Y) [15, 16]. The differential equations that describe the kinematic behavior of robot motion are the Eq. (2), where x and vare the particle position and velocity respectively [17].
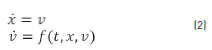
The kinematic behavior of the mobile robot is defined by the following state vector in the Eq. (3) [15, 16]. Also, the following space state equations represent the movement of each robot inside the plane, as the Eqs. (4) and (5) describe them, where uk is the vector that contains the system reference and the system outputs are the positions (X, Y) of each robot [18, 19].
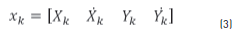
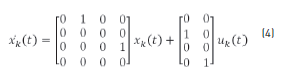
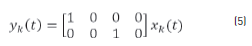
4. Leader-follower approach
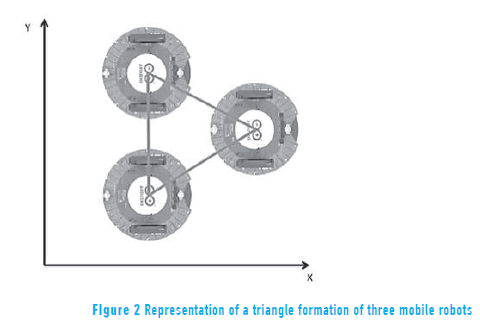
In the leader-follower approach, one robot is assigned as the leader of the group and the rest of the robots are the followers. The main function of the leader is to guide the group formation to follow the trajectory reference (1). Also, each follower must establish and maintain its position inside the formation in reference to the leader's movement. The followers only know the relative displacement of the other robots but just the leader knows the trajectory reference (see Figure 2).
To determine the error ek, the position of each robot xk is compared with the global position hkin the Eq. (6). After that, the errors of the adjacent robots are averaged in Ek , as the Eq. (7). Also, the relative position error zkof each robot is calculated with the difference between the error 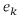 and the average error
and the average error  , proved in the Eq. (8). The objective of the control system is to reduce this relative error to 0, which means that the robots are in formation [20].
, proved in the Eq. (8). The objective of the control system is to reduce this relative error to 0, which means that the robots are in formation [20].
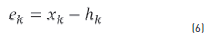

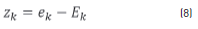
The equations that describe the robot movement have linearly independent variables, for this reason the system can be separated in two subsystems. Each one, describe the movement in one axis (X or Y) and is represented by the following space state Eqs. (9) and (10) and the transfer function Eqs. (11) and (12).
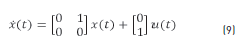
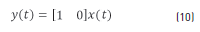
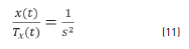

5. Fuzzy logic controller
The formation controller was designed to create any formation pattern using the leader-follower approach, where the leader has to follow the trajectory reference, and the followers have to maintain a specific position in relation to the leader. Robots can form various shapes in formation, the most common geometrical shapes are line and triangle, and both were tested in this article. The formation trajectory control is responsible to generate the linear velocities that each mobile robot must have to precisely follow the formation trajectory.
To control the group, the specific position of each robot inside the formation is necessary; each position is contained in the M formation, the Eq. (13) describes the matrix. With the reference trajectory and the formation position, the leader calculates and sends the specific global position that each robot must maintain; the result of the Eq. (14) is sent to each robot. It is important to note that any robot can be leader or follower, depending on the mode of operation assigned to each one.
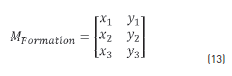
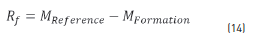
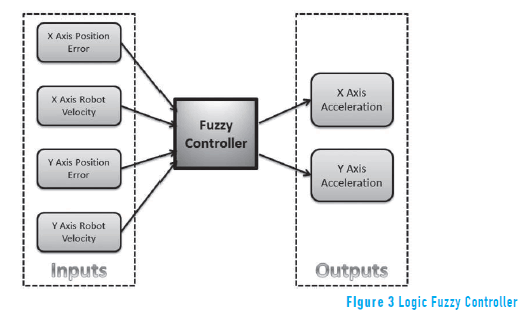
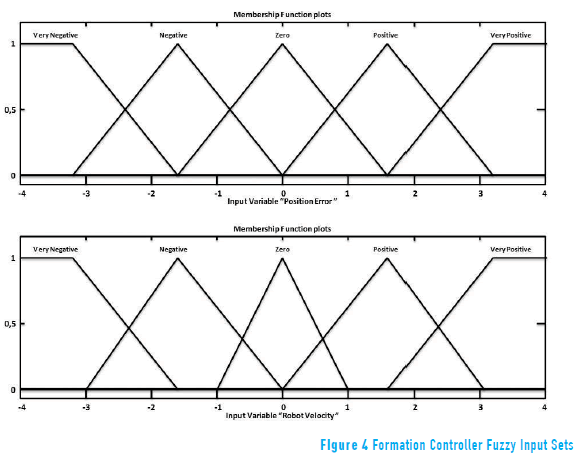
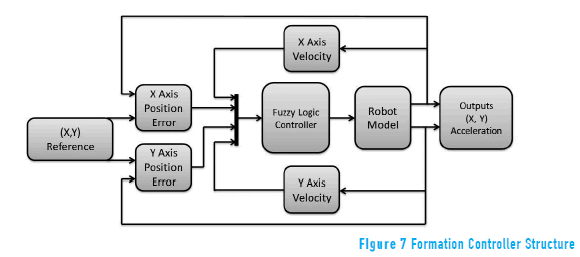
To develop an effective and computationally less expensive controller, triangular inputs and outputs were used since these are adequate for the requirements of the system. This formation fuzzy logic controller was developed with four inputs and a double output (see Figure 3). The inputs are the position errors and the actual lineal velocities for each axis, as the Eq. (15) describes (see Figure 4). On the other hand, the outputs of the controller are the lineal accelerations that the robot must have in each axis to reduce the error (see Figure 5). When the error of the position equates to zero, the robot is in the correct position inside the formation.
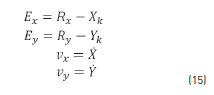
After analyzing the particle's movement inside the space, it was determined to control the position of each robot is necessary to know two specific things: the position error that each robot has and the way in which each one is moving (velocity). Consequently, the model does not consider external forces that perturb the movement. The fuzzy controller for evaluating the desired acceleration calculates the output depending if the robot has to slow down or accelerate in each axis. For example, if the robot presents a position error and does not have velocity, the controller should accelerate the robot, causing it to move toward the target. The situation would be different if the robot has the same position error but this time it has a positive velocity, in this case the controller should slow down the robot, causing it to stop into the target. Finally, if the robot is in the target, the controller should keep the robot in the same place without any velocity.
A total of 19 rules for each axis were used for the formation controller and they are presented in the Table 1, and the Figure 6 depicts the fuzzy action surface for each axis system under the fuzzy rules. The control surface shows that there are not strong changes, which generate extreme control actions, and permits to conclude that the system does not present abrupt actions as high accelerations or strong changes in the position of the wheels.
Since the X axis motion is not directly related to the movement of the Y one, it is possible to conclude that the variables are linearly independent, and for that reason, one fuzzy logic controller was implemented in each axis separately. To control all group formation each robot that forms part of the group must have the same fuzzy logic controller, and the interaction between all the robots makes the formation (see Figure 7).
To evaluate the fuzzy logic controller, its performance was compared with the PID controller developed in [14]. For each controller, the response produced by a step input was evaluated and the controllers were adjusted to produce the same over peak, with the objective to make a valid comparison. In the Table 2 the characteristic parameters calculated for each set of controllers are summarized. What is more, the Figure 8 shows the approximation curves to the final set point trajectory (Step), for each controller with same criteria.
Table 2 and Figure 8 shows the PID controller presents an over peak and content of ripple greater than its fuzzy counterpart, requiring almost the same time establishment. Although the PID controller acts at a higher speed, the fuzzy controller improve the values of some of the most important performance rates, such as the overshoot, oscillations and ripple factor.
6. Results
To test the control system developed in this article, several proofs of different type were developed by changing leader, reference and formation, looking to prove if the control works in a positive way. The first test was developed by simulating a group of three robots that maintains a triangular formation and follows a constant reference trajectory, with the robot R2 selected as a leader. The control response analysis allows concluding that the formation control system generates the right trajectories. These paths permit the group to follow the reference and maintain the desired pattern formation (see Figure 9).
After checking the leader robot, it successfully follows the reference trajectory and the follower robots are able to establish and maintain its position in the formation, the next test was developed by changing the reference each 30 seconds. This is the first method to avoid obstacles, since these can be avoided by changing the reference with the help of a vision system, implemented on an external computer that monitors the obstacles (see Figure 10).
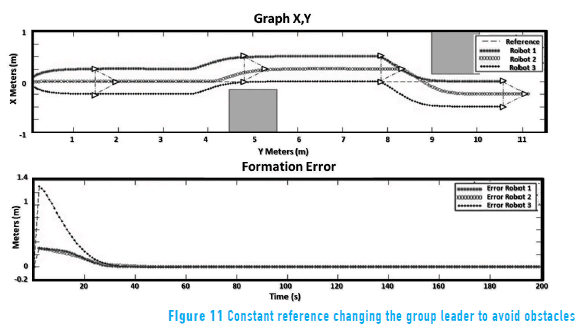
The following test was changing the group's leader with a constant reference. The group of robot must change the group leader in two cases. The first one is, if the actual leader presents a fault or it is lost; the second one, if a robot detects an obstacle in front of it, the leader of the group changes searching to avoid the obstacle (see Figure 11). This method presents an advantage since it does not need an external computer to work appropriately.
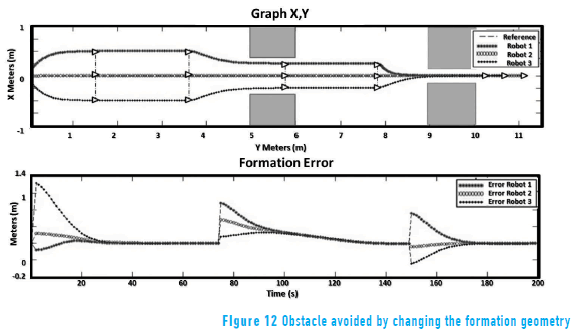
The next test was developed by changing the formation pattern, verifying if the control system allows the group to change it at any time. This is a useful tool in several situations, for example, it is a solution to move the group inside the restricted spaces or carry objects with different geometries. In this paper the change of formation was tested as a solution to avoid obstacles (see Figure 12).
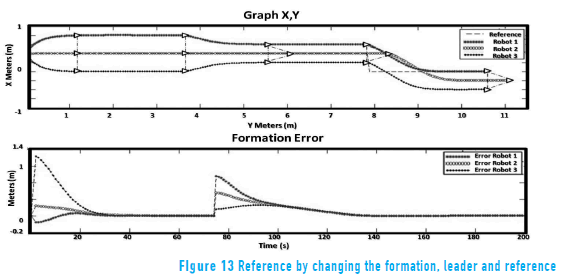
Finally, several changes that the control system allows were tested. At 10 seconds, the formation was changed; then, after 20 seconds, the reference and leader will change (see Figure 13). With this last test is established that the control system generates the references to maintain a formation while a target is followed, in addition to allowing the formation or leader to be changed at any time.
7. Conclusions
The first remarkable conclusion is that fuzzy controllers do not require a precise knowledge of the process, neither the exact model to perform its control; this was confirmed in the experimentation. Considering the quantitative information contained in Table 2, it was determined that the traditional control (PID), responds faster but with a bigger over peak that generates more ripples percentage than the fuzzy logic controller. Although, according to the settling time parameter the PID controller is 10% faster, it is possible to conclude that the Fuzzy logic controller is highly desirable in this control process, because it has fewer oscillations that improving the robot formations.
This work demonstrates that fuzzy logic can be used to solve the formation problem control, position control and avoid obstacles, and collisions control. The controller developed consists in a fuzzy logic formation controller, which is suitable for changing the desired formation and the leader of the group at any time. Also, the controller variability allows avoiding obstacles encountered on the group of robots way by changing the leader, the reference or the formation.
It was shown by means of simulation, that the control strategy has a good performance by generating the formation trajectories, because the leader robot leads the group to follow the reference trajectory, and followers' robots achieve to establish and maintain its position in the formation successfully. The formation trajectories generated by this controller can be used as a reference for tracking control system of any mobile robot moving in the plane (X, Y).
8. Acknowledgements
This work is supported by the project ING-1537 namely "Estudio de técnicas de control cooperativo descentralizado en formación de robots móviles no holonómicos –Fase II", funded by the research vice rectory of the Militar Nueva Granada University in Bogotá, Colombia.
9. References
1. K. Ng, M. Trivedi. Multirobot convoying using neuro-fuzzy control. Proceedings of the 13th International Conference on Pattern Recognition. Vol. 4. Vienna, Austria. 1996. pp. 417-421. [ Links ]
2. P. Varaiya. "Smart cars on smart roads: problems of control". IEEE Transactions on Automatic Control. Vol. 38. 1993. pp. 195-207. [ Links ]
3. M. Sisto, D. Gu. A fuzzy leader-follower approach to formation control of multiple mobile robots. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing, China. 2006. pp. 2515-2520. [ Links ]
4. I. Nourbakhsh, K. Sycara, M. Koes, M. Yong, M. Lewis, S. Burion. "Human-robot teaming for search and rescue". IEEE Pervasive Computing. Vol. 4. 2005. pp. 72-78. [ Links ]
5. M. Ghiasvand, K. Alipour. Formation control of wheeled mobile robots based on fuzzy logic and system dynamics. Proceedings of the 13th Iranian Conference on Fuzzy Systems (IFSC). Qazvin, Iran. 2013. pp. 1-6. [ Links ]
6. B. Young, R. Beard, J. Kelsey. A control scheme for improving multi-vehicle formation maneuvers. Proceedings of the American Control Conference. Vol. 2. Arlington, USA. 2001. pp. 704-709. [ Links ]
7. P. Tabuada, G. Pappas, P. Lima. Feasible formations of multi-agent systems. Proceedings of the American Control Conference. Vol. 1. Arlington, USA. 2001. pp. 56-61. [ Links ]
8. M. Amoozgar, K. Alipour, S. Sadati, M. Dehsara. Position control of multiple wheeled mobile robots using fuzzy logic. Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM). Montreal, Canada. 2010. pp. 587-592. [ Links ]
9. P. Song, A coordination framework for weakly centralized mobile robot teams. Proceedings of the IEEE International Conference on Information and Automation (ICIA). Harbin, China. 2010. pp. 77-82. [ Links ]
10. H. Mehrjerdi. "Hierarchical fuzzy cooperative control and path following for a team of mobile robots". IEEE/ASME Transactions on Mechatronics. Vol. 16. 2011. pp. 907-917. [ Links ]
11. X. Li, "Robot formation control in leader-follower motion using direct Lyapunov method". International Journal of Intelligent Control and Systems. Vol. 10. 2005. pp. 244-250. [ Links ]
12. A. Brandao, M. Sarcinelli, R. Carelli, T. Bastos. Decentralized control of leader-follower formations of mobile robots with obstacle avoidance. Proceedings of the IEEE International Conference on Mechatronics (ICM). Malaga, Spain. 2009. pp. 1-6. [ Links ]
13. A. Saffiotti. "The uses of fuzzy logic in autonomous robot navigation". Soft Computing. Vol. 1. 1997. pp. 180-197. [ Links ]
14. M. Molina, N. Velasco, L. Solaque, A. Riveros. Decentralized cooperative control technique for non-holonomic mobile formation. Proceedings of the III International Congress of Engineering Mechatronics and Automation (CIIMA). Cartagena, Colombia. 2014. pp. 1-5 [ Links ]
15. J. Veerman, G. Lafferriere, J. Caughman, A. Williams. "Decentralized control of vehicle formations". Systems & Control Letters. Vol. 54. 2005. pp. 899-910. [ Links ]
16. J. Veerman, G. Lafferriere, J.S. Caughman, A. Williams. "Flocks and formations". Journal of Statistical Physics. Vol. 121. 2005. pp. 901-936. [ Links ]
17. F. Bravo, D. Patino, K. Melo, C. Parra. Switching control and modeling of mobile robots formation. Proceedings of the IEEE IX Latin American and IEEE Colombian Conference on Automatic Control and Industry Applications (LARC) Robotics Symposium. Bogotá, Colombia. 2011. pp. 1-6. [ Links ]
18. K. Mathia, G. Lafferriere, T. Titensor. Cooperative control of UAV platoons – a prototype. Proceedings of the Euro UAV Conference and Exhibition. Paris, France. 2007. pp. 1-12. [ Links ]
19. A. Williams, G. Lafferriere, J. Veerman. Stable motions of vehicle formations. Proceedings of the 44th IEEE Conference on Decision and Control, and European Control Conference (CDC-ECC). Seville, Spain. 2005. pp. 72-77. [ Links ]
20. J. Fax, R. Murray. "Information flow and cooperative control of vehicle formations". IEEE Transactions on Automatic Control. Vol. 49. 2004. pp. 1465-1476. [ Links ]