Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.78 Medellín Mar. 2016
https://doi.org/10.17533/udea.redin.n78a04
DOI: 10.17533/udea.redin.n78a04
ARTÍCULO ORIGINAL
Effect of different combinations of size and shape parameters in the percentage error of classification of structural elements in vegetal tissue of the pumpkin Cucurbita pepo L. using probabilistic neural networks
Efecto de diferentes combinaciones de parámetros de tamaño y forma en el porcentaje de error de la clasificación de elementos estructurales en tejido vegetal de Cucurbita pepo L. 'Calabaza', utilizando redes neuronales probabilísticas
Jimy Frank Oblitas-Cruz1*, Wilson Manuel Castro-Silupu2, Luis Mayor-López3
1Facultad de Ingeniería, Universidad Privada del Norte. Av. Del Ejército 920 - Urb. El Molino. C. P. 13007. Trujillo, Perú.
2Facultad de Ingeniería y Ciencias Agrarias, Universidad Nacional Toribio Rodríguez de Mendoza de Amazonas. El Franco - Barrio de Higos Urco. Chachapoyas, Perú.
3Instituto de Agroquímica y Tecnología de Alimentos, Universidad Politécnica de Valencia. Camino de Vera, s/n. C. P. 46022. Valencia, España.
* Corresponding author: Jimy Frank Oblitas Cruz, e-mail: jimy.oblitas@upn.edu.pe
(Received September 25, 2014; accepted September 14, 2015)
ABSTRACT
The optimal combination of size and shape parameters for classifying structural elements with the lowest percentage error is determined. For this purpose, logical sequences and a series of micrographs of tissues of the pumpkin Cucurbita pepo L. were used to identify and manually classify structural elements into three different classes: cells, intercellular spaces and unrecognizable elements. From each element, eight parameters of size and shape (area, equivalent diameter, major axis length, minor axis length, perimeter, roundness, elongation and compaction) were determined, and a logical sequence was developed to determine the combination of parameters that generated the lowest error in the classification of the microstructural elements by comparison with manual classification. It was found by this process that the minimum error rate was 12.7%, using the parameters of major axis, minor axis, perimeter and roundness.
Keywords: Combination, size and shape parameters, probabilistic neural network
RESUMEN
Se procedió a determinar la combinación óptima de parámetros de tamaño y forma a fin de obtener la clasificación de elementos estructurales con el menor porcentaje de error. Para este efecto se procedió a utilizar secuencias lógicas y una serie de micrografías de tejido de Cucurbita pepo L.'calabaza' a partir de las cuales se determinaron y clasificaron manualmente los elementos estructurales en tres diferentes clases (células, espacios intercelulares y elementos no reconocibles). De cada elemento se determinaron ocho parámetros de tamaño y forma (área, diámetro equivalente, longitud eje mayor, longitud eje menor, perímetro, redondez, elongación, compactación), se elaboró una secuencia lógica para determinar la combinación de parámetros que generaba el menor error en la clasificación de los elementos microestructurales, mediante comparación con la clasificación manual y se determinó con este proceso que el mínimo porcentaje de error fue 12,7%, mediante el uso de los parámetros de eje mayor, eje menor, perímetro y redondez.
Palabras clave: Combinación, parámetros de tamaño y forma, redes neuronales probabilísticas
1. Introduction
With wider markets opening up and with the accompanying developments in marketing methods, it has become necessary to address more sophisticated consumer demands with regard to the quality characteristics of food products. This has imposed on food science the requirement to develop means to determine the relationships between the structure of a foodstuff, its properties and its functionality, since, in addition to the basic components present in a foodstuff, the ways in which these are arranged have a significant effect on the properties and attributes demanded by consumers [1-4].
The arrangement of these basic components has various levels of complexity and effects on functionality, with the structure of the product as a whole often being the result of the rearrangement of previous, less complex, structures during processing. Thus, the properties of the food product are ultimately the result of successive compositional and structural changes in the raw material which is the result of the physical and chemical phenomena that occur during processing: heat and mass transfer in multiphase systems, microstructural and macrostructural changes (including deformation and relaxation of structural elements), enzymatic reactions, phase transitions, etc. [3, 5-9].
In view of the above, for a proper design of food products and processes, it is necessary to understand and to be able to model changes in the structure of food during the transformation process and to predict the relationship between these structural changes and the properties of the end product. However, existing models are unrealistic, paying little attention to structure and structural changes [3], mainly because of the high complexity and heterogeneity of the structure at different levels (nano, micro, meso and macro) [6, 10].
At present, these structure–property–process relationships are poorly understood and models based upon them have a limited range of application [5, 11]. It is therefore necessary to clarify which components and interactions of these complex systems are the most significant, so a model that is able to generate results can be developed and can be extrapolated to different processing conditions [7].
Among the different levels of structural complexity, the most influential and perhaps one of the least understood is the microstructure. At a microstructural level, it is necessary to consider the structure and chemistry of the cell wall, the turgor pressure and the means of access of fluid to the cell, and, at higher levels, the structure of the tissue (cell orientation, number of pores and intercellular spaces) and types of tissues or organs [4].
There have been a number of studies (e.g. [12, 13, 14]) of the structure–property–process relationships in materials subjected to osmotic dehydration and convective drying. By examining the changes generated in mechanical properties as a result of density changes and alterations in the tissue (cell breakage and formation of air pockets), these investigations have shown that the structure before, during and after processing affects mass transfer, mechanical properties and textural properties.
From the above considerations, it can be seen that one of the major challenges facing food science and engineering is the characterization and prediction of the structural changes that food undergoes during processing and the effect of these changes on the properties of the final food product—in other words, the structure–property–process relationships [5, 15, 16]. It is therefore necessary to develop and implement methodologies for analyzing structure at different levels and incorporate these into the development of more realistic models.
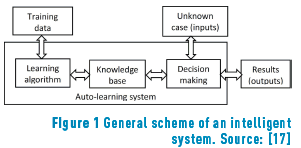
In this context, it is appropriate to consider the use of an intelligent system; the general scheme is shown in Figure 1. Such systems have been successfully used in classification of fruit according to parameters related to maturity [15]. Because of their self-learning capability, these systems could be applied to recognition of the constituent elements in plant tissues (cells and intercellular spaces).
In these systems, images are quantitatively characterized according to morphological characteristics and color parameters, among others; these are used to represent the food and to train the system. Using these researched data previously classified, the researcher trains the data into an intelligent classification system, providing the ability to classify the unknown cases and simulate the way a trained user performs the classification task [17-19].
Decisions based on patterns of shape, size, color, etc. have been used successfully in fruit classification, harvest time prediction, muscle texture analysis, assessment of size distribution and identification of seeds and leaves, assessment of extruded food, and plant structure analysis [16, 20, 21].
Although current advances in computer capabilities have allowed the construction of sophisticated machines to replace human actions, there is still a large gap in those activities that require simulation of the five senses, especially when this is aimed at systems of classification and prediction based on pattern recognition [18, 19, 22, 23].
In this context, computer-generated artificial classifiers try to imitate decisions using both neural networks and Bayesian discriminants [21, 24], interacting with a database at all levels of the process to provide greater accuracy and more effective use of the information from that database in decision making [17, 25].
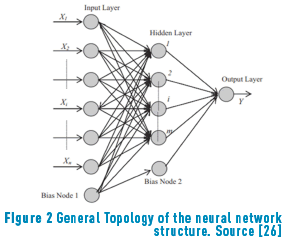
Neural networks, initially inspired by the human nervous system, combine the complexity of statistical techniques with self-learning, imitating the human cognitive process. Figure 2 illustrates the typical topology of a neural network structure; the entire network is a very complicated set of interdependences and may incorporate some degree of nonlinearity [16].
2. Methodology
2.1. Samples
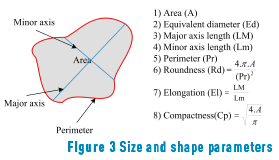
Micrographs of the pumpkin Cucurbita pepo L. were used: parenchymal tissue cylinders of the intermediate zone of the mesocarp were obtained, parallel to the major axis of the fruit, and were treated according to the method of [9]. These micrographs were characterized by parameters related to the size and shape of their constituent elements, as shown in Figure 3.
2.2. Methods
a) Development of program for analysis of size and shape parameters of plant tissue
The program used to analyze the plant tissue microstructure was implemented in the mathematical software Matlab v.2010a. This program gets parameters of size and shape of the structural elements of tissue and used to power the intelligent classification system based on probabilistic neural networks.
The details of the program analysis and classification of structural elements are as follows:
- Interface pretreatment. This interface, generically called the guide in the Matlab software, allows the user to load the micrograph in JPEG format (with standard compression and digital image coding), producing a three-dimensional matrix to which standard matrix operations can be applied to perform image enhancement.
- Interface restoration and classification. The user is able to perform restoration operations (such as removal of spaces and skeletonization). This restoration procedure is followed by segmentation (separation of the elements that constitute the tissue coloring into elements of different colors), which creates an image called matrix L. In this interface, automatic classification of elements as cells, intercellular spaces and unrecognizable elements is also performed, generating a labeled image.
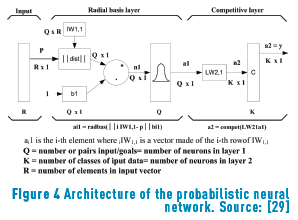
The system is based on a probabilistic neural network called newppn. This is a feed forward network. It is specialized for classification when an input is presented. The first layer computes distances from the input vector to the training input vectors and produces a vector whose elements indicate how close the input is to a training input. The second layer sums these contributions for each class of inputs to produce as its net output a vector of probabilities. Finally, a competitive output layer picks the maximum of these probabilities, and produces a 1 for that class and a 0 for the other classes. The design parameter of this probabilistic neural network is the spread of the radial basis transfer function [27, 28]. Little or no training is required for a probabilistic neural network (except for spread optimization), so the architecture shown in Figure 4 is used.
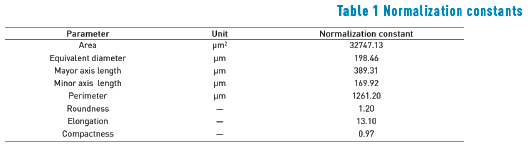
Each size and shape parameter of the structural elements was first normalized by dividing by a corresponding normalization constant from a matrix for normalization (Table 1). Each normalization constant was the value that achieves 0.95 in cumulative frequency distribution for the respective parameter.
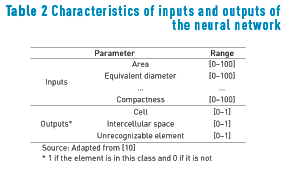
Whether or not an output neuron was determined by three class identifiers, expressed in binary code (Table 2). With this, the classification process was ended.
b) Selection and application of shape parameters in recognition system
To determine the effect of different combinations of parameters on the classification of structural elements using the probabilistic neural network, the parameters were coded as shown in Table 3. The combinations of parameters are determined to avoid repetition and regardless of the order within each combination.
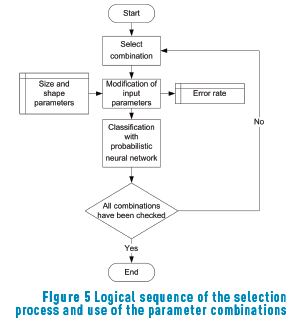
The parameter combinations were used as input to the classification process in the neural network. Figure 5 shows the logical sequence for the selection and use of parameter combinations in the intelligent classification system.
The classification was performed on a total of 322 elements, of which 169 were cells, 99 intercellular spaces and 54 unrecognizable elements.
c) Evaluation of the error rate in the classification of structural elements
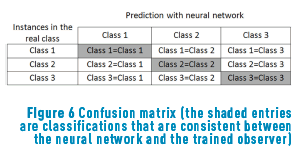
The classification results were then compared with the results of manual classification performed by a trained operator. The efficiency of the classification of the neural network was calculated using a confusion matrix, Figure 6; matrix determines overall classification efficiency and also the confusion between classes. Consequently, it is a visualization tool used in supervised learning in this, each column represents the number of predictions of each class, while each row represents the instances in the actual class.
d) Determination of combination of size and shape parameters generating the optimal classification
To find the combination of parameters that generates the optimal classification, the combination with the highest weighted efficiency rating was determined. This procedure also takes into account the efficiency ranking with regard to cells and intercellular spaces.
3. Results
3.1. Informatics application
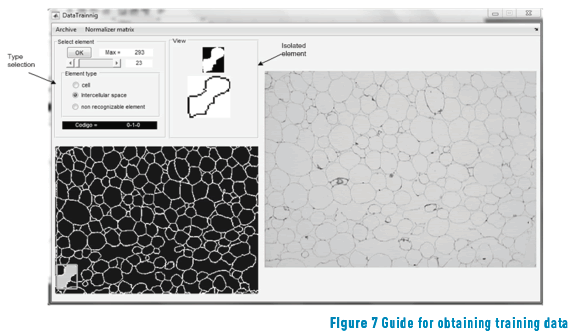
The source code was developed, as described in Section 2.2a, and implemented in Matlab; this consisted of an interface for extracting information of size and shape parameters in micrographs and train probabilistic neural networks with combinations of the above parameters. This interface was developed specially trained to allow users to discriminate different structural elements, through a logical sequence and guides specially developed for this purpose (Figure 7).
3.2. Application of different combinations of size and shape parameters
It is proceeded to determine the number of combinations of parameters of shape and size according to the function (1):
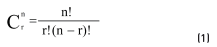
Where:
n = number of parameters of size and shape
r = number of parameters of group [2-7]
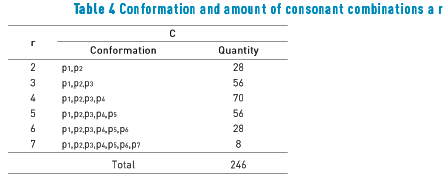
Table 4 details the formation, distribution of parameters pi, and amount of combinations.
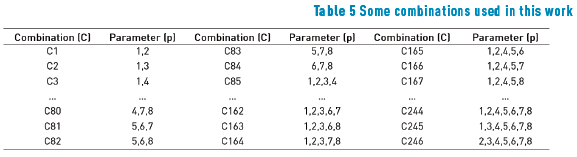
The sequence of parameters that make up each combination was determining implementing an algorithm in Matlab script. Table 5 shows some combinations obtained with the script before and used in this work.
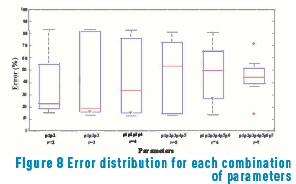
Subsequently, each combination of input parameters was evaluated in the standings through the neural network, determining the percentage of error for each combination. The distribution of errors in chart, boxes and whiskers, shown in Figure 8.
The box-and-whisker plot in Figure 8 shows, for each combination of parameters, the minimum error rate as the lower whisker. It should be noted that for most of the combinations, 50% of the data is within the interquartile range.
The optimal combination of parameters is obtained by minimizing the error, as shown in Figure 9; these codes are commented in Table 5.
Figure 9 shows that this classification system, based on a probabilistic neural network is able to sort through a good approximation to the various structural elements in the cellular tissue of Cucurbita pepo L., getting errors mean errors between 12.7 and 14.6%. These results support the potential use of artificial intelligence in combination with computer vision systems for classification and structure prediction in food products [15, 30-33].
4. Discussion
In the classification of structural elements in plant tissues, different combinations of input parameters generate different results [17, 33]. However, it appears that neural networks are suitable for classification processes, and, largely because of their "black-box" nature, they exhibit great flexibility. In our case, the topology of the model could be adjusted by using different combinations of input parameters.
Figure 8 shows that different combinations of size and shape parameters yield different results in the classification process; these parameters have already been considered in other investigations [9, 16]. The collection of cases presented in [17] shows that in both the fresh and processed food sectors, artificial intelligence and neural networks can be used for classification purposes. However, it is also on the experimental results of several researchers that the main difficulty is the heterogeneity of criteria when determining the classification technique used in one case in particular; that is the reason why studies with [19] have been developed to compare the technique of regression of partial least-squares and more adequate architecture of the network or neural networks neural networks applied in a study in particular.
Figure 8 also shows that the error rate can be high, and only for some cases, there is a relatively low misclassification rate compared with the manual procedure. Errors as high as 7.5-25% have been found in classification of fish quality in blocks of 5% and as high as 11.5% in classification of the quality of fresh carrots [17].
5. Conclusions
Different combinations of input parameters in a probabilistic neural network used for classifying structural elements in plant tissues generate different levels of error. Exploratory data analysis showed that the combination with minimum error rate is found by combining four input size and shape parameters.
It was found that the minimum error rate, 12.7%, was obtained with a combination of the parameters of major axis, minor axis, perimeter, and roundness.
6. References
1. N. Acevedo, V. Briones, P. Buera and J. Aguilera, "Microstructure affects the rate of chemical, physical and color changes during storage of dried apple discs", Journal of Food Engineering, vol. 85, no. 2, pp. 222-231, 2008. [ Links ]
2. O. Fennema, S. Damodaran and K. Parkin, Food chemistry, 4th ed. Florida, USA: CRC Press, 2008. [ Links ]
3. P. Fito, M. LeMaguer, N. Betoret and P. Fito, "Advanced food process engineering to model real foods and processes: The 'SAFES' methodology", Journal of Food Engineering, vol. 83, no. 2, pp. 173-185, 2007. [ Links ]
4. L. Mayor, J. Pissarra and A. Sereno, "Microstructural changes during osmotic dehydration of parenchymatic pumpkin tissue", Journal of Food Engineering, vol. 85, no. 3, pp. 326-339, 2008. [ Links ]
5. P. Fito, "Modelos de relaciones estructura-propiedad-proceso en alimentos reales. Herramientas y aplicaciones", in VIII Iberoamerican Congress of Food Engineering (CIBIA), Lima, Perú, 2011. [ Links ]
6. L. Seguí, P. Fito and P. Fito, "A study on the rehydration ability of isolated apple cells after osmotic dehydration treatments", Journal of Food Engineering, vol. 115, no. 2, pp. 145-153, 2013. [ Links ]
7. L. Seguí, P. Fito and P. Fito, "Analysis of structure-property relationships in isolated cells during OD treatments. Effect of initial structure on the cell behaviour", Journal of Food Engineering, vol. 99, no. 4, pp. 417-423, 2010. [ Links ]
8. J. Aguilera, D. Stanley and K. Baker, "New dimensions in microstructure of food products", Trends in Food Science & Technology, vol. 11, no. 1, pp. 3-9, 2000. [ Links ]
9. L. Mayor, J. Pissarra and A. M. Sereno, "Microstructural changes during osmotic dehydration of parenchymatic pumpkin tissue", Journal of Food Engineering, vol. 85, no. 3, pp. 326-339, 2008. [ Links ]
10. W. Castro, L. Mayor, L. Segui and P. Fito, "Aplicación de redes neuronales a la clasificación de elementos estructurales en micrografias de tejido vegetal", VIII Iberoamerican Congress of Food Engineering (CIBIA), Lima, Perú, 2011. [ Links ]
11. H. Mebatsion, P. Verboven, Q. Ho, B. Verlinden and B. Nicolaï, "Modelling fruit (micro)structures, why and how?", Trends in Food Science & Technology, vol. 19, no. 2, pp. 59-66, 2008. [ Links ]
12. J. Barat, P. Fito and A. Chiralt, "Modeling of simultaneous mass transfer and structural changes in fruit tissues", Journal of Food Engineering, vol. 49, no. 2-3, pp. 77-85, 2001. [ Links ]
13. N. Mavroudis, P. Dejmek and I. Sjöholm, "Osmotic-treatment-induced cell death and osmotic processing kinetics of apples with characterised raw material properties", Journal of Food Engineering, vol. 63, no. 1, pp. 47-56, 2004. [ Links ]
14. L. Mayor, R. Cunha and A. Sereno, "Relation between mechanical properties and structural changes during osmotic dehydration of pumpkin", Food Research International, vol. 40, no. 4, pp. 448-460, 2007. [ Links ]
15. A. Nieto, D. Salvatori, M. Castro and S. Alzamora, "Structural changes in apple tissue during glucose and sucrose osmotic dehydration: shrinkage, porosity, density and microscopic features", Journal of Food Engineering, vol. 61, no. 2, pp. 269-278, 2004. [ Links ]
16. L. Mayor, R. Moreira and A. Sereno, "Shrinkage, density, porosity and shape changes during dehydration of pumpkin (Cucurbitapepo L.) fruits", Journal of Food Engineering, vol. 103, no. 1, pp. 29-37, 2011. [ Links ]
17. C. Du and D. Sun, "Learning techniques used in computer vision for food quality evaluation: a review", Journal of Food Engineering, vol. 72, no. 1, pp. 39-55, 2006. [ Links ]
18. A. Mizushima and R. Lu, "An image segmentation method for apple sorting and grading using support vector machine and Otsu's method", Computers and Electronics in Agriculture, vol. 94, pp. 29-37, 2013. [ Links ]
19. A. Fernandes et al., "Comparison between neural networks and partial least squares for intra-growth ring wood density measurement with hyperspectral imaging", Computers and Electronics in Agriculture, vol. 94, pp. 71-81, 2013. [ Links ]
20. M. El-Bakry and J. Sheehan, "Analysing cheese microstructure: A review of recent developments", vol. 125, pp. 84-96, 2014. [ Links ]
21. M. Omid, M. Khojastehnazhand and A. Tabatabaeefar, "Estimating volume and mass of citrus fruits by image processing technique", Journal of Food Engineering, vol. 100, no. 2, pp. 315-321, 2010. [ Links ]
22. K. Daqrouq and T. Tutunji, "Speaker identification using vowels features through a combined method of formants, wavelets, and neural network classifiers", Applied Soft Computing, vol. 27, pp. 231-239, 2015. [ Links ]
23. K. Nakano, "Application of neural networks to the color grading of apples", Computers and Electronics in Agriculture, vol. 18, no. 2-3, pp. 105-116, 1997. [ Links ]
24. F. Pernkopf and M. Wohlmayr, "Stochastic margin-based structure learning of Bayesian network classifiers", Pattern Recognition, vol. 46, no. 2, pp. 464-471, 2013. [ Links ]
25. T. Brosnan and D. Sun, "Improving quality inspection of food products by computer vision––a review", Journal of Food Engineering, vol. 61, no. 1, pp. 3-16, 2004. [ Links ]
26. S. Alacali, B. Akbas and B. Doran, "Prediction of lateral confinement coefficient in reinforced concrete columns using neural network simulation", Applied Soft Computing, vol. 11, no. 2, pp. 2645-2655, 2011. [ Links ]
27. F. Fernández, C. Hervás, P. Gutiérrez and M. Carbonero, "Evolutionary -Gaussian radial basis function neural networks for multiclassification", Neural Networks, vol. 24, no. 7, pp. 779-784, 2011. [ Links ]
28. W. Huang, S. Oh and W. Pedrycz, "Design of hybrid radial basis function neural networks (HRBFNNs) realized with the aid of hybridization of fuzzy clustering method (FCM) and polynomial neural networks (PNNs)", Neural Networks, vol. 60, pp. 166-181, 2014. [ Links ]
29. H. Demuth and M. Beale, Neural network toolbox for use with Matlab: User's Guide, 1st ed. Natick, USA: MathWorks, Inc., 2002. [ Links ]
30. C. Du and D. Sun, "Automatic measurement of pores and porosity in pork ham and their correlations with processing time, water content and texture", Meat Science, vol. 72, no. 2, pp. 294-302, 2006. [ Links ]
31. S. Kumar and G. Mittal, "Rapid detection of microorganisms using image processing parameters and neural network", vol. 3, pp. 741-751, 2010. [ Links ]
32. B. Ozyildirim and M. Avci, "Generalized classifier neural network", Neural Networks, vol. 39, pp. 18-26, 2013. [ Links ]
33. B. Zhang et al., "Principles, developments and applications of computer vision for external quality inspection of fruits and vegetables: A review", Food Research International, vol. 62, pp. 326-343, 2014. [ Links ]