Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista Facultad de Ingeniería Universidad de Antioquia
versão impressa ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.79 Medellín abr./jun. 2016
https://doi.org/10.17533/udea.redin.n79a08
ARTÍCULO ORIGINAL
DOI: 10.17533/udea.redin.n79a08
Model-based maximum power point tracking for wind generators
Seguimiento del punto de máxima potencia basado en modelo para generadores eólicos
Andrés Julián Saavedra-Montes*, Carlos Andrés Ramos-Paja, Carlos Alejandro Ramírez-Gómez
Departamento de Energía Eléctrica y Automática, Facultad de Minas, Universidad Nacional de Colombia, Carrera 80 # 65-223 - Núcleo Robledo. A. A. 1027. Medellín, Colombia
* Corresponding author: Andrés Julián Saavedra Montes, e-mail: ajsaaved@unal.edu.co
DOI: 10.17533/udea.redin.n79a08
(Received June 26, 2015; accepted March 28, 2016)
ABSTRACT
A model-based maximum power point tracking solution for wind systems is presented in this paper. The strategy uses the Loss-free resistor concept and a generator model, which relates the load impedance required to produce the maximum power depending on the generator rotor speed. The strategy performance is validated through simulation and the emulation of a multi-machine wind generation system. With the proposed strategy, it is possible to extract the maximum power of each generator and, therefore, the maximum power of the generation system.
Keywords: Power optimization, wind generation, loss-free resistor, multi-machine wind system
RESUMEN
En este artículo se presenta una estrategia de seguimiento del punto de máxima potencia, basada en modelo para generadores eólicos. La estrategia utiliza el concepto del resistor libre de pérdidas y un modelo del generador, el cual representa la impedancia de carga requerida para producir la máxima potencia posible en la velocidad del rotor del generador. Los resultados de la estrategia son validados a través de simulación y una emulación de un sistema con múltiples aerogeneradores. Con la estrategia propuesta es posible extraer la máxima potencia de cada generador y, por lo tanto, la máxima potencia del sistema de generación.
Palabras clave: Optimización de potencia, generación eólica, resistor libre de pérdidas, sistema eólico multi-máquina
1. Introduction
In the last decades, a common effort has been made to reduce the fuel oil dependence in several production and operating systems, because fuel oil utilization is an important cause of global warming and its consequences [1]. A strategy to support the demand of electric power, removing pressure from fuel oil production, is to extract electric power from alternative sources; therefore, wind generation systems have been developed as one of those alternative sources [2].
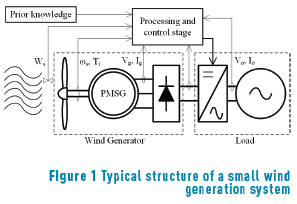
Wind energy has been a promising and effective source to provide electric power. Among the several wind generation systems implemented around the world, there are small wind generation systems, which are ranged from 200W to 5 kW, with a typical structure that is illustrated in Figure 1. The energy produced by wind generation systems depends on the wind speed, among other variables, and for each speed condition, it is possible to extract a corresponding maximum power [3, 4]. In order to achieve such maximum power production, maximum power point tracking (MPPT) algorithms are implemented in the processing stage of the system. Several MPPT algorithms are presented in the literature, where the most common ones are the tip speed ratio (TSR) control, the turbine torque control, and the perturb and observe strategy.
In TSR control, the generator speed n is regulated to keep an optimum TSR. To implement this algorithm, the wind speed Ws and the rotor speed of the wind turbine _s must be measured; additionally, a function between the power coefficient and the TSR is required [5]. The torque control strategy brings the wind generation system to the optimum torque which is associated with the optimum TSR. This algorithm requires the measurement of the turbine angular speed and the turbine mechanical torque Ti, additionally a previous knowledge of the optimum torque and the maximum power coefficient is required; however, the measurement of the wind speed is not necessary. In the perturb and observe algorithm, an input variable is perturbed, which can be the generator current, i.e. the input current to the converter, and the change in the output power is observed. If the change is positive, the input variable is perturbed again in the same direction; however, if the output power change is negative, the input variable is perturbed in an opposite direction. This process is repeated continuously to track the maximum power point (MPP) [3]. The perturb and observe strategy does not require to measure the wind speed or the turbine angular speed, either previous knowledge about the system, because the algorithm is independent of the turbine characteristic [5]. The main challenge for the algorithm is to track fast the changes of the wind speed because the generation system can arrive to the maximum power with some delay [3]. Other important challenge is the step size selection, because large steps mean fast response but also larges oscillation around the maximum power, i.e. high power losses. On the other hand, small steps improve the steady-state efficiency but reduce the convergence speed to the maximum power [6, 7].
In order to tackle some of the challenges related with small wind generation systems, a Model-Based MPPT (MB-MPPT) algorithm is proposed in this paper, which is implemented in two small wind generation systems. The implementation of the algorithm reduces the amount of sensors and control units required in contrast with other strategies, increasing the economic viability of small wind generation systems working together.
The rest of the paper is organized as follows: In Section 2 the MPP of a permanent magnet synchronous generator is analytically and experimentally illustrated. In the next section, the MB-MPPT is proposed and the Loss-Free Resistor (LFR) concept is introduced. Also, the MPPT strategy is experimentally validated and contrasted with a voltage control strategy. In Section 4, an application example of the MB-MPPT control, which consists of a multi-machine wind system controlled by the MB-MPPT is presented. Finally, conclusions in Section 5 close the paper.
2. Maximum power point in a permanent magnet synchronous generator
A reduced model of a permanent magnet synchronous generator (PMSG) is analyzed in order to illustrate its maximum power point. The output power of a three phase synchronous generator calculated from its per phase terminal voltage Vg and its armature current Ig is given by (1):
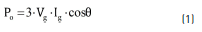
To obtain the MPP for a specific armature current value, the dPo/dIg is equated to zero (2):
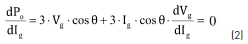
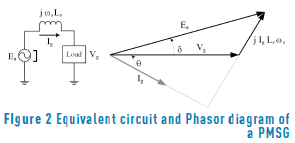
In (2), the dependence of generator terminal voltage from the armature current is observed, therefore, a function that solves the generator terminal voltage in function of the armature current is needed. That expression is obtained from the phasor diagram corresponding to an operating point of the PMSG. The phasor diagram, presented in Figure 2, is derived from its equivalent circuit.
In Figure 2, δ is the power angle, θ is the power factor angle, Ls is the inductance of the machine in H, ωs is the generator rotor speed in rad/s, and Ea is the electromotive force in V. The dependence of the generator terminal voltage from the armature current is obtained from the single-phase phasor diagram representing the generator in a specific operating point. Expression (3) is a geometric relation obtained from Figure 2, and for this analysis Ea, Ls and _s are considered constants:
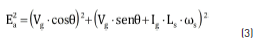
Solving Vg from (3), the relation of the terminal voltage as a function of the armature current is given by (4):
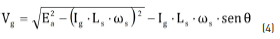
Replacing (4) in (2) leads to expression (5), which corresponds to the armature current value Ig_MPP at the MPP.
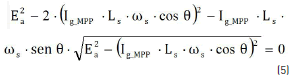
Solving the generator armature current from (5) leads to the expression to calculate the Ig_MPP given in (6). The current value is obtained for known values of the power factor, the electromotive force, the machine inductance, and the rotor speed. Finally, replacing Ig_MPP in (1) enables to calculate the MPP.

To illustrate the MPP, a small wind generation system was emulated in a power laboratory. The emulator is presented in Figure 3, where the PMSG was emulated with a synchronous generator keeping constant its field current. The wind turbine was emulated with an induction motor and its AC driver, which was used to change rotor speed.
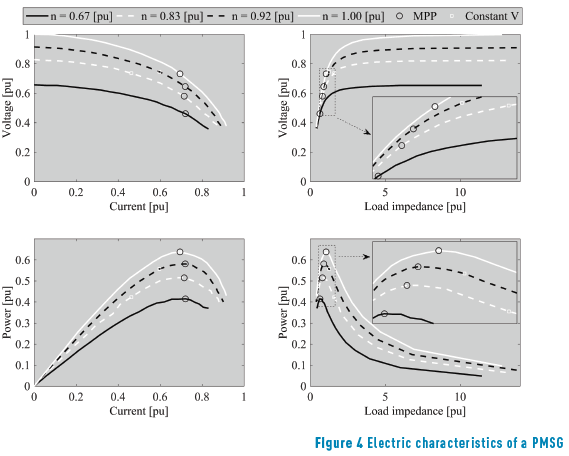
The generator terminal voltage and the generator output power were plotted in Figure 4 in function of the armature current and the load impedance. The four electric characteristics are plotted at four different rotor speeds, which were kept constant and are expressed in per unit (pu).
In Figure 4 the MPP is highlighted with black circles. In all the electric characteristics, the power extracted using a constant voltage control strategy is highlighted with white circles. From the figure, it is clear why a MPPT strategy is a better option to extract the maximum power from a small wind generation system in contrast with a constant voltage strategy. The power vs. load impedance characteristics point out there is a specific load impedance value that enables the extraction of the maximum power from the small wind generation system. Expression (7) models the optimal load impedance ZR depending on _s obtained from the experiments.
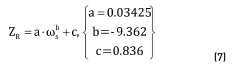
3. Model-based MPPT
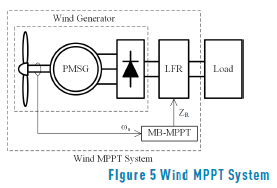
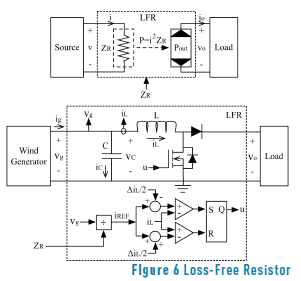
Based on the MPP model previously presented in (7), it is possible to calculate the optimal impedance that must be connected to the wind generator to extract the maximum power for any wind speed. However, since in classical wind power systems, e.g. Figure 1, the load imposes its impedance to the generator, it is necessary to insert an additional device between the wind generator and the load to perform an optimal impedance matching: set the impedance of the generator according to (7) to provide the maximum power possible to the load, which in turns exhibits any impedance different from (7). The device that fulfills such conditions is known as ''Loss-Free Resistor'' (LFR), which requires a control algorithm to define its input impedance ZR.
The LFR control algorithm must measure the generator speed n to set ZR according to (7), hence such a controller behaves as an optimization algorithm to track the optimal operation condition of the wind generator. Therefore, the control algorithm defining ZR from (7) is a Model-Based Maximum Power Point Tracker or MB-MPPT. Figure 5 illustrates the proposed Wind MPPT System (MPPTS) based on the LFR controlled by the MB-MPPT.
3.1. LFR implementation
The implementation of LFR is performed using dc/dc power converters as described in [8, 9]. In the particular case of the grid-connected wind MPPTS, two conditions must be provided by the LFR: first, the current requested to the generator must have low harmonic content to avoid damages [10], and second, the LFR must provide a boosting factor to match the generator voltage with the higher voltage of full-bridge inverters, which are standard for small power grid connections. Hence, this paper proposes the implementation of the LFR using a boost converter.
The top of Figure 6 presents the concept of a LFR used to impose the impedance of a power source. The LFR input port behaves as a variable impedance, while its output port behaves as a power source transferring the input power to the load. The bottom of Figure 6 shows the implementation of the LFR using a boost converter, where the generator impedance Zg = Vg/Ig must be regulated; Vg and Ig stand for the generator voltage and current, respectively. Due to the non-linear nature of Zg, a non-linear controller must be used to implement the LFR: the boost converter must be controlled to behave as a resistance at its input terminals.
From the circuit in Figure 6, the switched differential Eq. (8) describing the inductor current is obtained, where u = {0, 1} represents the binary control signal used to close {1} and open {0} the Mosfet. Then, representing the generator voltage Vg in terms of the rotor speed ws, the rotational constant k and the generator resistance Rg as Vg = k×w – Rg×Ig, the differential Eq. (9) describing Vg is obtained.
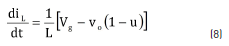
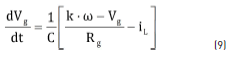
The Sliding-Mode Control (SMC) technique was selected to implement the LFR due to its non-linear nature and its binary control signal, which matches the binary nature of the Mosfet and diode. The approach used to design the SMC is the following: since the averaged value of the inductor current within the switching period corresponds to the generator current, i.e. volt-second balance where dVg/dt = 0 in (9) [11], a SMC is designed to regulate the averaged inductor current following a reference iREF, which in turns define the generator current. Then, iREF is calculated from the generator voltage Vg to guarantee the desired generator impedance ZR.
The sliding surface Sx adopted to regulate the inductor current iL is given in (10), which also describes the first sliding condition Sx = 0. The second sliding condition is given in (11) [12].
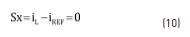
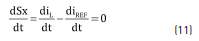
Three additional conditions must be fulfilled to guarantee the existence of the sliding-mode [12], which in turns guarantee the correct reference tracking and stability: transversality, equivalent control and reachability. The former one stands for the system controllability, where the control variable u must be present in the sliding surface derivative, i.e. the derivative with respect to u must be different from zero. Eq. (12) verifies that the proposed surface fulfills the transversality condition.
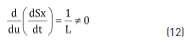
The equivalent control condition stands for the system stability, where the averaged value ueq of the control variable u must be constrained between the binary values of u, i.e. 0 < ueq < 1. Replacing u by ueq in (8), Eq. (13) describing ueq is obtained. Then, when the system is trapped within the sliding mode, i.e. Sx = 0 and iL = iREF, the condition 0 < ueq < 1 leads to (14), which describes the constraints that must be fulfilled by iREF to ensure the system stability. Hence, if the derivative of iREF fulfills (14), the sliding-mode is granted and the inductor current is successfully defined by iREF. It must be noted that the limits in (14) correspond to the physical limits of the inductor current derivative [11], hence the SMC provides the fastest behavior achievable by the converter.
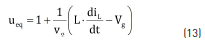
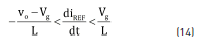
The reachability condition stands for the ability to reach the sliding surface [12], where it is required that the derivative of the states drives the system towards the sliding surface. In such a way, considering the proposed sliding surface Sx, two options are possible: first, the inductor current is higher than the reference current, i.e. iL > iREF or Sx > 0, second the inductor current is lower than the reference current, i.e. iL < iREF or Sx < 0. When iL > iREF it is required to reduce the inductor current, which implies opening the Mosfet and closing the diode (u = 0), while iL < iREF requires to increase the inductor current, which implies closing the Mosfet and opening the diode (u = 1). From such conditions, the reachability of the surface is granted by the control actions given in (15).
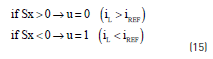
Such control law can be implemented using classical comparators. But, since near iL = iREF the switching frequency of the comparators, hence of the control command of the Mosfet, could become infinite due to the chattering phenomenon [11], the control law must be implemented using hysteric-comparators. Such a solution is standard in the implementation of SMC for power converters [11], where a hysteresis band H is imposed to limit the switching frequency of the converter. In the LFR case, the band is set to H = DiL and the control law is implemented as in (16). The bottom of Figure 6 illustrates the scheme of the proposed SMC, which uses a flip-flop S-R to hold the state of u defined by the implementation of (16).
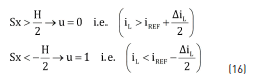
Since the proposed SMC fulfills the transversality condition, it is controllable. Moreover, since it fulfills the reachability condition, the system is driven to the sliding surface from any operation condition. In addition, since the equivalent control condition is fulfilled, when the system reaches the sliding surface it will be trapped there. Those conditions ensure an accurate tracking of the reference iREF; hence the inductor behaves as a current source to define the generator current ig. The last part of the LFR implementation is defining the SMC reference as iREF = Vg /ZR, where ZR stands for the LFR impedance reference. In such a way, since Ig = iREF, the impedance of the generator Zg is defined by ZR.
Finally, to ensure the SMC correct behavior, condition (14) must be fulfilled. From (9), (10) and (11), and taking into account that iL = iREF = Ig = Vg /ZR, the equivalent behavior of the controlled system is given by (17). Therefore, the generator voltage behaves as a first order system with settling time ts. Then the capacitor C must be selected to constraint diREF/dt = (1/ZR)×dVg/dt based on the limit (worst-case) values of k, ws, Vg, Rg and ZR: maximum k, maximum ws, minimum Vg, minimum Rg and maximum ZR.
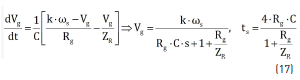
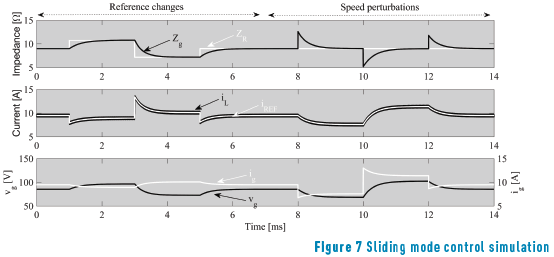
Based on the experimental bench described in Section 2, the following nominal parameters are adopted to illustrate the SMC performance: k×w = 282.16 V, Vg = 95 V, Rg = 20.73 W, ZR = 9 W, L = 250 mH, C = 50 mF, vo = 200 V, DiL = 500 mA. Figure 7 presents the system simulation, where changes on the impedance reference ZR are introduced at 1 ms (+20 %), 3 ms (-40 %) and 5 ms (+20 %); while changes on the rotor speed w are introduced at 8 ms (-20 %), 10 ms (+40 %) and 12 ms (-20 %). The SMC ensures the correct LFR behavior in all the perturbation conditions, where Zg follows ZR with a settling time ts = 1.26 ms as predicted by (17).
3.2. Experimental results
The experiments were carried out under three different wind speeds: the first condition imposes a rotor speed of 0.83 pu up to 40 s, then the speed was changed to 0.92 pu, and at 78 s the speed was changed again to 1.00 pu.
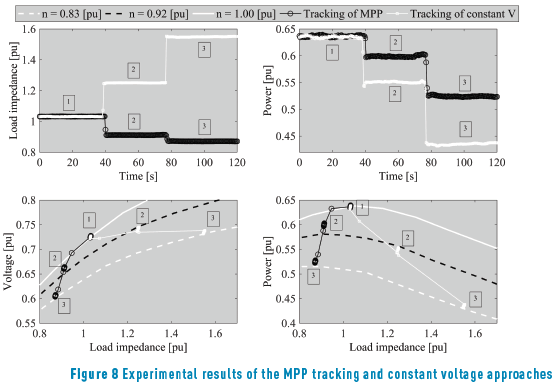
A first experiment was conducted by setting constant the generator voltage to 0.75 pu for all the operation conditions. The second experiment was performed by controlling the generator impedance in agreement with (7), which effectively tracks the MPP. The results of those experiments are presented in Figure 8, in both time domain and phase planes.
Figure 8 presents the impedance imposed to the generator (top-left) and the power produced (top-right) for both constant voltage and MPP tracking approaches. Such experimental results confirm the higher power production achieved with the proposed MB-MPPT strategy. Figure 8 also shows, at the bottom, the operating points in terms of impedance, voltage and power. Those phase planes confirm the accurate voltage regulation in the constant voltage approach, while the MPP tracking approach imposes a variable generator voltage to increase the power production.
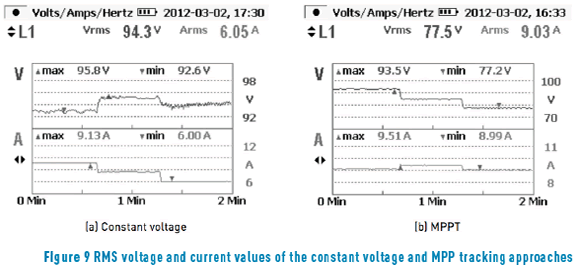
Figure 9 presents the experimental single-phase voltage and current RMS values for both experiments, which confirm the phase planes data reported in Figure 8.
4. Application example: a multi-machine wind system
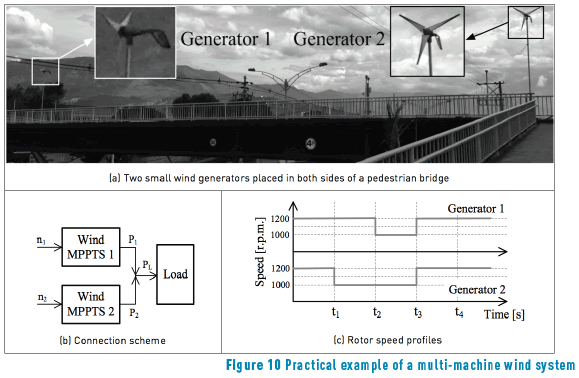
In urban environments, it is common to experience space restrictions that lead to divide the power production among multiple smaller wind-generators instead of a single larger device. This is the case of bridge mounted wind generators, where unbalance weight could be detrimental to the structural health of the bridge and pedestrians safety. An example of this practice is presented in Figure 10(a), where two wind generators are placed in opposites sides of a bridge.
This application example considers each wind generator regulated by a MB-MPPT controller as in Figure 5, where both generators supply the same load, e.g. a single grid-connected inverter. Figure 10(b) presents the connection scheme for those wind generators. Moreover, since both generators are placed at opposite sides of the bridge, different wind speed profiles are assumed, which produce the rotor speed profiles depicted in Figure 10(c).
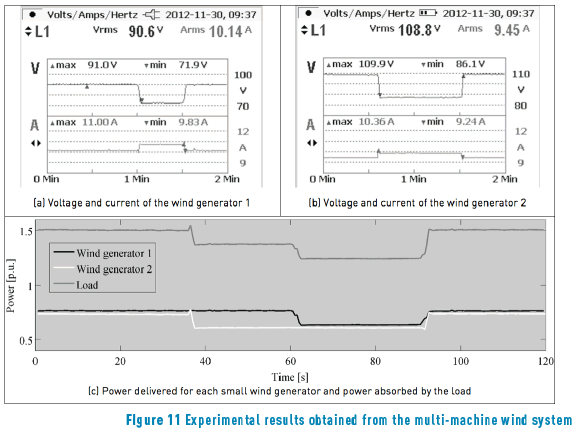
Two experimental units with the structure described in Figure 5 were used to represent both bridge mounted wind generators, where both wind turbine emulators where configured to impose the speed profiles given in Figure 10(c). The experimental results obtained with such a multi-machine wind system are presented in Figure 11. The single-phase voltage and current profiles of both generators are presented in Figure 11(a) and 11(b), while the three-phase power profiles produced by both generators are presented in Figure 11(c). In addition, such a figure also presents the power profile absorbed by the load.
This application example shows the usefulness of the proposed control technique to maximize the power produced by wind generation systems. Moreover, it is noted that, despite the number of generation units, the control complexity is not significantly increased.
5. Conclusions
A model-based maximum power point tracking for a multi-machine wind system was implemented. The tracking strategy uses the LFR concept and a PMSG model, which represents the load impedance to generate the maximum power for each generator rotor speed. This model and the generator rotor speed are the requirements to implement the strategy, which are less demanding than the requirements of commonly adopted MPPT strategies, therefore the strategy becomes a viable option when the MPPT is intended.
During the emulation of a wind generation system, the maximum power of each generator and therefore the maximum power of the whole generation system were extracted. The experimental results of the MPP tracking and constant voltage approaches illustrate the effectiveness of the proposed strategy in the extraction of the maximum power.
The main drawback of this solution concerns the requirement of parameterizing offline the optimal generator impedance. An improvement on this aspect could be done by adopting identification techniques that enable to correct ZR in agreement with the generator aging.
6. Acknowledgments
This work has been supported by Universidad Nacional de Colombia under the project MICRO-RED-26861 and by Colciencias (Fondo nacional de financiamiento para la ciencia, la tecnología y la innovación Francisco José de Caldas) under the project MicroRENIZ-25439 (Code 1118-669-46197) and the doctoral scholarship 095-2005.
7. References
1. L. Barroso, H. Rudnick, F. Sensfuss and P. Linares, ''The Green Effect'', IEEE Power Energy Mag., vol. 8, no. 5, pp. 22-35, 2010. [ Links ]
2. R. Moreno, G. Strbac, F. Porrua, S. Mocarquer and B. Bezerra, ''Making Room for the Boom'', IEEE Power Energy Mag., vol. 8, no. 5, pp. 36-46, 2010. [ Links ]
3. M. Abdullah, A. Yatim, C. Tan and R. Saidur, ''A Review of Maximum Power Point Tracking Algorithms for Wind Energy Systems'', Renew. Sustain. Energy Rev., vol. 16, no. 5, pp. 3220-3227, 2012. [ Links ]
4. S. Musunuri and H. Ginn, ''Comprehensive Review of Wind Energy Maximum Power Extraction Algorithms'', in IEEE Power and Energy Society General Meeting, San Diego, USA, 2011, pp. 1-8. [ Links ]
5. Y. Zhu, M. Cheng, W. Hua and W. Wang, ''A Novel Maximum Power Point Tracking Control for Permanent Magnet Direct Drive Wind Energy Conversion Systems'', Energies, vol. 5, no. 5, pp. 1398-1412, 2012. [ Links ]
6. C. Pan and Y. Juan, ''A Novel Sensorless MPPT Controller for a High-Efficiency Microscale Wind Power Generation System'', IEEE Trans. Energy Convers, vol. 25, no. 1, pp. 207-216, 2010. [ Links ]
7. J. Hui and A. Bakhshai, ''A New Adaptive Control Algorithm for Maximum Power Point Tracking for Wind Energy Conversion Systems'', in Power Electronics Specialists Conference (PESC), Rhodes, Greece, 2008, pp. 4003-4007. [ Links ]
8. A. Cid et al., ''Synthesis of Loss-Free Resistor based on Sliding-Mode Control and its Applications in Power Processing'', Control Eng. Pract., vol. 21, no. 5, pp. 689-699, 2013. [ Links ]
9. D. Shmilovitz, ''On the Control of Photovoltaic Maximum Power Point Tracker via Output Parameters'', IEE J. Electr. Power Appl., vol. 152, pp. 239-248, 2005. [ Links ]
10. Y. Xia, K. Ahmed and B. Williams, ''Different Torque Ripple Reduction Methods for Wind Energy Conversion Systems Using Diode Rectifier and Boost Converter'', in IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, Canada, 2011, pp. 729-734. [ Links ]
11. R. Erickson and D. Maksimovic, Fundamentals of Power Electronics, 2nd ed. Springer Science and Business Media, 2007. [ Links ]
12. D. Gonzalez, C. Ramos and R. Giral, ''Improved design of sliding mode controllers based on the requirements of MPPT techniques'', IEEE Trans. Power Electron., vol. 31, no. 1, pp. 235-247, 2015. [ Links ]