Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería Universidad de Antioquia
Print version ISSN 0120-6230
Rev.fac.ing.univ. Antioquia no.79 Medellín Apr./June 2016
https://doi.org/10.17533/udea.redin.n79a09
ARTÍCULO ORIGINAL
DOI: 10.17533/udea.redin.n79a09
On-line signature verification using Gaussian Mixture Models and small-sample learning strategies
Verificación de firmas en línea usando modelos de mezcla Gaussianas y estrategias de aprendizaje para conjuntos pequeños de muestras
Gabriel Jaime Zapata-Zapata1, Julián David Arias-Londoño2*, Jesús Francisco Vargas-Bonilla1, Juan Rafael Orozco-Arroyave1,3
1Departamento de Ingeniería Electrónica y Telecomunicaciones, Universidad de Antioquia. Calle 67 # 53-108. A. A. 1226. Medellín, Colombia.
2Departamento de Ingeniería de Sistemas, Universidad de Antioquia. Calle 67 # 53-108. A. A. 1226. Medellín, Colombia.
3Pattern Recognition Lab, Friedrich-Alexander University Erlangen-Nürnberg. Martensstraβe 3. 91058. Erlangen, Germany.
* Corresponding author: Julián David Arias Londoño, e-mail: julian.ariasl@udea.edu.co
DOI: 10.17533/udea.redin.n79a09
(Received May 30, 2015; accepted February 08, 2016)
ABSTRACT
This paper addresses the problem of training on-line signature verification systems when the number of training samples is small, facing the real-world scenario when the number of available signatures per user is limited. The paper evaluates nine different classification strategies based on Gaussian Mixture Models (GMM), and the Universal Background Model (UBM) strategy, which are designed to work under small-sample size conditions. The GMM's learning strategies include the conventional Expectation-Maximisation algorithm and also a Bayesian approach based on variational learning. The signatures are characterised mainly in terms of velocities and accelerations of the users' handwriting patterns. The results show that for a genuine vs. impostor test, the GMM-UBM method is able to keep the accuracy above 93%, even when only 20% of samples are used for training (5 signatures). Moreover, the combination of a full Bayesian UBM and a Support Vector Machine (SVM) (known as GMM-Supervector) is able to achieve 99% of accuracy when the training samples exceed 20. On the other hand, when simulating a real environment where there are not available impostor signatures, once again the combination of a full Bayesian UBM and a SVM, achieve more than 77% of accuracy and a false acceptance rate lower than 3%, using only 20% of the samples for training.
Keywords: On-line signature verification, Gaussian Mixture Models, Universal Background Model, Variational GMM-Supervector, Bayesian learning
RESUMEN
El artículo aborda el problema de entrenamiento de sistemas de verificación de firmas en línea cuando el número de muestras disponibles para el entrenamiento es bajo, debido a que en la mayoría de situaciones reales el número de firmas disponibles por usuario es muy limitado. El artículo evalúa nueve diferentes estrategias de clasificación basadas en modelos de mezclas de Gaussianas (GMM por sus siglas en inglés) y la estrategia conocida como modelo histórico universal (UBM por sus siglas en inglés), la cual está diseñada con el objetivo de trabajar bajo condiciones de menor número de muestras. Las estrategias de aprendizaje de los GMM incluyen el algoritmo convencional de Esperanza y Maximización, y una aproximación Bayesiana basada en aprendizaje variacional. Las firmas son caracterizadas principalmente en términos de velocidades y aceleraciones de los patrones de escritura a mano de los usuarios. Los resultados muestran que cuando se evalúa el sistema en una configuración genuino vs. impostor, el método GMM-UBM es capaz de mantener una precisión por encima del 93%, incluso en casos en los que únicamente se usa para entrenamiento el 20% de las muestras disponibles (equivalente a 5 firmas), mientras que la combinación de un modelo Bayesiano UBM con una Máquina de Soporte Vectorial (SVM por sus siglas en inglés), modelo conocido como GMM-Supervector, logra un 99% de acierto cuando las muestras de entrenamiento exceden las 20. Por otro lado, cuando se simula un ambiente real en el que no están disponibles muestras impostoras y se usa únicamente el 20% de las muestras para el entrenamiento, una vez más la combinación del modelo UBM Bayesiano y una SVM alcanza más del 77% de acierto, manteniendo una tasa de falsa aceptación inferior al 3%.
Palabras clave: Verificación de firmas en línea, Modelos de Mezclas Gaussianas, Modelo Histórico Universal, GMM-Supervector Variacional, aprendizaje Bayesiano
1. Introduction
Biometrics measures individuals' unique physical or behavioural characteristics with the aim of recognising or authenticating identity. The most common physical biometrics include fingerprints, hand or palm geometry, retina, iris, or facial characteristics, among others. On the other hand, behavioural characteristics include signature, voice (which also has a physical component), keystroke pattern, and gait, among others. According to [1], signature and voice technologies are one of the most developed. The handwritten signature is recognised as one of the most widely accepted personal attributes for identity verification. The signature is a symbol of consent and authorisation, especially in the credit card and bank-checks environment, and has been an attractive target of fraud for a long time. Currently, there is a growing demand for the processing of individual identification to be faster and more accurate, therefore the design of a robust automatic signature verification system becomes an important challenge.
A comparison of signature verification with other recognition technologies, e. g. fingerprint, face, voice, retina and iris scanning, reveals that signature verification has several advantages as an identity verification mechanism. Firstly, signature analysis can only be applied when the person is/was conscious and willing to write in the usual manner. To give a counter example, a fingerprint may also be used when the person is unconscious, i.e. drugged state. Forging a signature is deemed to be more difficult than forging a fingerprint, given the availability of sophisticated methods [2].
Unfortunately, signature verification is a difficult discrimination problem since a handwritten signature is the result of a complex process depending on the physical and psychological conditions of the signer, as well as the conditions of the signing process [3]. There are two major methods of signature verification. One is an on-line method to measure sequential data, such as handwriting speed and pen pressure, with a special device. The other one is an off-line method that uses an optical scanner to obtain handwriting data written on paper. The dynamic information of the pen-tip (stylus) movement such as pen-tip coordinates, pressure, velocity, acceleration, and pen-up/pen-down, can be captured by a tablet in real time but not by an image scanner [4].
The normal variability of signatures constitutes the greatest obstacle to be met in achieving automatic verification. Signatures vary in their complexity, duration, and vulnerability to forgery [5]. Moreover, signers vary in their coordination and consistency. Problems of signature verification are addressed by taking into account three different types of forgeries [6]: random forgeries, produced without knowing either the name of the signer nor the shape of its signature; simple forgeries, produced knowing the name of the signer but without having an example of his signature; and skilled forgeries, produced by people who attempt to imitate the original signature with prior knowledge of it. Clearly, the problem of signature verification becomes more and more difficult when passing from random to simple and skilled forgeries, the latest being a much more difficult task even more considering that humans use to make errors in several cases. Indeed, exercises in imitating a signature often allow humans to produce forgeries very similar with respect to the originals, making their discrimination practically impossible. In many cases, the distinction is complicated even more by the large variability introduced by some signers when writing their own signatures [4].
Unlike conventional pattern recognition systems, where every object to be recognised/classified is represented as a feature vector, the on-line signature verification (OSV) requires the processing of time dependent signals where every signature produces a set of feature vectors (one per instant of time). Since the observations at the time t are not independent from the previous observations, this problem has been addressed by means of stochastic models able to model that dependence, such as hidden Markov models (HMM) [7]. In most of the cases, the number of available samples for training the system is small, so one of the main challenges of the OSV problem, is to build a system able to achieve high recognition rates with a small number of training samples. This fact implies an important drawback for systems based on HMM because it is well-known that the large number of parameters of a HMM requires a large number of training samples in order to a get a properly fit of the model.
The assumption of independence among the observations is a strategy successfully applied in the speaker verification field. In this case, the verification task can be seen as a multiple-instance learning problem, where, instead of receiving a set of instances which are individually labelled, the system receives a set of labelled bags, where each bag is the set of observations representing a signature. This approach allows the use of models with less computational load and lower requirements on the number of training samples. This work explores the use of different strategies based on a class of generative models called Gaussian Mixture Models (GMM), which have the advantage of being able to process signals with different length, such as the ones coming from on-line digitised signatures, without the need of a previous standardisation of the signal length. This kind of models have been extensively used for speaker recognition [8], and they have also been tested for on-line signature verification [9]. GMMs are conventionally trained using the Expectation-Maximisation (EM) algorithm, which is an implementation of the Maximum Likelihood criterion. The EM algorithm provides a simple and quick way to train a GMM. However, it presents three main drawbacks. First of all, the EM algorithm requires a considerable number of samples for training the models. Second, it is sensitive to overfitting, i.e., it fits to the training data but lacks the generalisation ability to make accurate predictions for new data, and finally, it does not provide a compact way to estimate the correct number of Gaussian components M, so it must be set using a cross-validation strategy. In order to overcome the first two pointed out limitations, in [8], it was proposed a training strategy called GMM-Universal Background Model (GMM-UBM). It consists in training a ''universal'' model (a class independent GMM adjusted from all the observations in the universe), and using a Bayesian adaptation procedure to transform the UBM into a class-dependent model. This strategy has proved to achieve better results than the conventional GMM strategy [8, 10]. Following this approach, a system combining the advantage of discriminative and generative models was proposed in [11]. The system used a UBM, and more precisely, the mean vectors of user-dependent adapted GMM, to construct a new feature space where a Support Vector Machine (SVM) was employed to take the final decision. This method is typically called GMM-Supervector (GMM-SVM).
Although the UBM and GMM-SVM approaches have obtained significant improvements in comparison to the standard GMM strategy, in both cases the training of the UBM is still based on the EM algorithm, and its corresponding drawbacks remain. Recently, a full Bayesian learning for GMM has been proposed [12], which transforms the GMM into a hierarchical Bayesian model assigning prior distributions to the GMM parameters. The training algorithm based on this approach is called Variational EM, and in addition to show better performance under small sample size conditions, it provides a semi-automatic way to select the optimum number of Gaussian components, with the consequent reduction of the computational load during the training stage.
This paper addresses the problem of on-line signature verification and evaluates nine different classification strategies based on GMM, including a new variational version of the GMM-SVM model. The main aim of the work is to determine whether the strategies based on UBM, can reduce the requirements on the size of training set, in order to enable verification systems to operate in real situations, i.e. when the number of signatures available per user is quite limited. The paper is organised as follows: section 2 presents the features used to characterise the signatures and the classification methods; section 3 exposes the database and the experimental setup, as well as the results obtained. Finally, section 4 presents some conclusions derived from the results.
2. Methods
2.1. Characterization
The input signals from a digitising tablet include the position in the Xand Yaxes, and the pressure (pr) along the time during the writing of the signature. The position in the Xand Y axes were used to derive six additional dynamical features as suggested in [7]. The set of features includes:
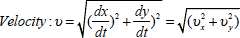 The logarithm of the velocity was also included using
The logarithm of the velocity was also included using 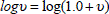
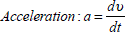
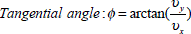
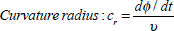
In a similar way to the velocity, the logPressure defined as 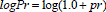 was also included. Therefore, for every instant of time tthe feature vector Otwas composed of eleven features as follows (see Eq. (1)):
was also included. Therefore, for every instant of time tthe feature vector Otwas composed of eleven features as follows (see Eq. (1)):
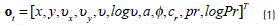
A whole signature is then represented by the complete set of feature vectors observed at different times, which can be expressed as (see Eq. (2)):
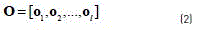
Where lis the length of the signature in terms of time instants.
2.2. Modelling and recognition
From a pattern recognition point of view, the classification of the signatures defined as in the Eq. (2), can be understood as a multi-instance learning problem [13]. In this work, this problem is addressed using several strategies based on Gaussian Mixture Models (GMM), with the aim of providing a system able to work under conditions of small number of training samples.
Gaussian Mixture Models - GMM
A GMM is a parametric probability density function represented as a weighted sum of Gaussian component densities. GMMs are commonly used in different tasks as a parametric model of the probability distribution of continuous measurements [8]. Formally a GMM can be expressed as (see Eq. (3)):
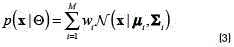
Where xis a ρ-dimensional continuous-valued data vector (i.e. measurements of features), 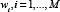 are the mixtures weights, and
are the mixtures weights, and 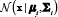 are the Gaussian components. Each component is a ρ-variate multivariate Gaussian function, with mean vector
are the Gaussian components. Each component is a ρ-variate multivariate Gaussian function, with mean vector 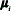 and covariance matrix
and covariance matrix 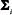 . The mixture weights satisfy the constraints
. The mixture weights satisfy the constraints 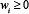 and
and 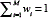 . The complete GMM is parametrised by the mean vectors, covariance matrices and mixture weights from all component densities. These parameters are collectively represented by the notation (see Eq. (4)):
. The complete GMM is parametrised by the mean vectors, covariance matrices and mixture weights from all component densities. These parameters are collectively represented by the notation (see Eq. (4)):
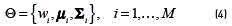
There are several techniques available for estimating the parameters of a GMM; however, traditionally, the most employed technique is the maximum likelihood (ML) estimation [14]. The ML estimation technique finds parameters that maximize the joint likelihood of the training data which are supposed to be independent and identically distributed (iid). Given a set X of N iid observations of ρfeatures 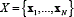 , the GMM likelihood can be written as (see Eq. (5)):
, the GMM likelihood can be written as (see Eq. (5)):
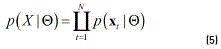
Although this expression is a non-linear function of the parameters 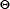 , the joint likelihood can be maximized with a simple and efficient update procedure called Expectation-Maximisation (EM) algorithm [14].
, the joint likelihood can be maximized with a simple and efficient update procedure called Expectation-Maximisation (EM) algorithm [14].
Once the parameters of the GMM were calculated, the detection system is a straight-forward generative classifier. For each class to be recognised (genuine or impostor), the parameters of a different GMM are estimated (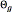 and
and 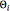 ). Thus, the evaluation is carried out calculating a likelihood ratio, in which for each GMM the a posteriori probability of a particular feature sequence
). Thus, the evaluation is carried out calculating a likelihood ratio, in which for each GMM the a posteriori probability of a particular feature sequence 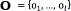 (extracted from a particular signature) is estimated. Applying the Bayes' rule and discarding constant prior probabilities, the likelihood ratio in the log domain becomes (see Eq. (6)) [15]:
(extracted from a particular signature) is estimated. Applying the Bayes' rule and discarding constant prior probabilities, the likelihood ratio in the log domain becomes (see Eq. (6)) [15]:
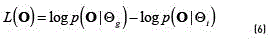
The likelihood ratio is compared with respect to a threshold λ in order to take a decision, accept or reject the signature. In the biometric verification research fields, typically the threshold λis set to the Equal Error rate threshold [16].
It is worth emphasising that, since the OSV task corresponds to a multi-instance learning, the terms in the log likelihood ratio must be computed as (see Eq. (7)):
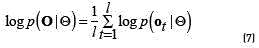
where the  scale factor is used to normalise the likelihood with respect to the duration of the signature, avoiding a possible bias due to different pattern lengths of correct and impostor signers. Note that lis the number of feature vector composing a single signature, while N in Eq. (5) is the total number of feature vectors per class (including multiple signatures).
scale factor is used to normalise the likelihood with respect to the duration of the signature, avoiding a possible bias due to different pattern lengths of correct and impostor signers. Note that lis the number of feature vector composing a single signature, while N in Eq. (5) is the total number of feature vectors per class (including multiple signatures).
Universal Background Model
The GMM-Universal Background Model (GMM-UBM) is a training strategy where all the available samples are used for training a ''universal'' model (a conventional GMM), and the class-dependent models are adapted from the UBM. There are several adaptation procedures proposed in the literature, but the most widely used are:
 using the Bayes formula (see Eq. (8)) [17]:
using the Bayes formula (see Eq. (8)) [17]: 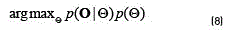
Where 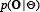 is the likelihood function of Ogiven the model parameters. The adaptation can be performed on all of the parameters of the model, even though in some applications it has been found that the most important parameters to be adapted are the mean vectors [8]. MAP assumes the prior distribution for the mean vectors as Gaussian. The adaptation rules are derived using the EM algorithm, which balances the new estimates on the adaptation data and the prior knowledge. For the mean vectors the adaptation is performed according to (see Eq. (9)):
is the likelihood function of Ogiven the model parameters. The adaptation can be performed on all of the parameters of the model, even though in some applications it has been found that the most important parameters to be adapted are the mean vectors [8]. MAP assumes the prior distribution for the mean vectors as Gaussian. The adaptation rules are derived using the EM algorithm, which balances the new estimates on the adaptation data and the prior knowledge. For the mean vectors the adaptation is performed according to (see Eq. (9)):
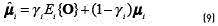
where 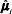 is the adapted mean vector for the component i,
is the adapted mean vector for the component i,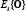 is the expected mean feature vector for the adaptation data, and
is the expected mean feature vector for the adaptation data, and 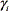 is the adaptation factor that controls the balance between the new data and prior knowledge. It can be estimated as (see Eq. (10)) [8]:
is the adaptation factor that controls the balance between the new data and prior knowledge. It can be estimated as (see Eq. (10)) [8]:
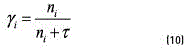
where 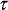 is a fixed relevant factor.
is a fixed relevant factor. 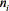 is similar to the cumulated responsibility of the component iin the generation of the new data O, i.e. the E step of the EM algorithm (see Eqs. (11) and (12)). Formally
is similar to the cumulated responsibility of the component iin the generation of the new data O, i.e. the E step of the EM algorithm (see Eqs. (11) and (12)). Formally
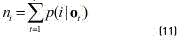
where
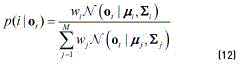
The expected mean 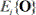 corresponds to the M step of the EM algorithm and can be estimated as (see Eq. (13)):
corresponds to the M step of the EM algorithm and can be estimated as (see Eq. (13)):
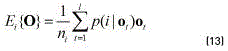

where 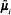 is the extended mean vector
is the extended mean vector 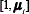 , required in order to include the bias term during the linear regression. The
, required in order to include the bias term during the linear regression. The 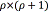 matrix A is estimated using a EM algorithm with auxiliar function given by (see Eq. (15)) [18]:
matrix A is estimated using a EM algorithm with auxiliar function given by (see Eq. (15)) [18]:
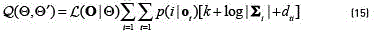
where k is the constant 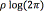 ,and
,and 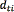 is the argument of the Gaussian function given by
is the argument of the Gaussian function given by 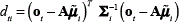 .
.
GMM-Support Vector Machine
This method was proposed in [11] and combines the modelling properties of the GMM-UBM scheme, with the discrimination capabilities of the Support Vector Machines (SVM) [19]. The method consists on building an UBM in the same way as the former approach, but unlike the GMM-UBM where the adapted model is class-dependent (genuine/impostor), in this case one adaptation per each single signature is performed, and the mean vectors of the adapted GMM are used to construct a GMM supervector that becomes in the new feature vector representing the signature, i.e. the GMM-UBM is used as a mapping between the original feature sequence O and the super vector 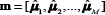 . Finally, the feature space constructed by stacking all the supervectors from the different signatures is used to feed a conventional classification stage based on SVM.
. Finally, the feature space constructed by stacking all the supervectors from the different signatures is used to feed a conventional classification stage based on SVM.
Variational Bayesian GMM
The Variational GMM (VGMM) is a hierarchical Bayesian model in which the parameters of the GMM are treated as random variables themselves with their corresponding prior distributions. The prior distribution imposed over the mixing coefficients 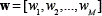 is a Dirichlet distribution, where by symmetry, the same parameter
is a Dirichlet distribution, where by symmetry, the same parameter 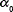 is used for each of the components (see Eq. (16)). The parameter
is used for each of the components (see Eq. (16)). The parameter 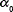 can be interpreted as the effective number of observations associated with each component in the mixture [14]. Similarly, the method introduces an independent Gaussian-Wishart prior governing the mean and precision (the inverse of the covariance matrix
can be interpreted as the effective number of observations associated with each component in the mixture [14]. Similarly, the method introduces an independent Gaussian-Wishart prior governing the mean and precision (the inverse of the covariance matrix 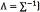 of each Gaussian component (see Eq. (17)) [14]. Formally,
of each Gaussian component (see Eq. (17)) [14]. Formally,
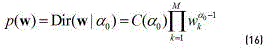
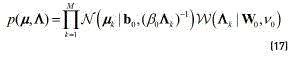
where 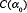 is the normalisation constant for the Dirichlet distribution, and
is the normalisation constant for the Dirichlet distribution, and 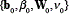 are the hyperparameters of the Gaussian-Wishart distribution.
are the hyperparameters of the Gaussian-Wishart distribution. 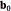 is the hypermean of the mean distribution which is typically set to 0by symmetry [14],
is the hypermean of the mean distribution which is typically set to 0by symmetry [14], 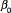 is a scaling factor,
is a scaling factor, 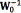 is the scale matrix, and
is the scale matrix, and 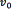 is called the ''degrees of fredom'', which must satisfy
is called the ''degrees of fredom'', which must satisfy 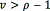 .
. 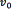 controls how strong the confidence is on the prior
controls how strong the confidence is on the prior 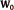 [20]. The training of this model can be achieved by an analogous algorithm to the EM called Variational EM (VEM), which, as the EM algorithm, also requires a proper initialisation of the hyperparamters [21]. The optimisation of the variational posterior distribution can also be split into two steps: the E step, where the current distributions over the model parameters are used to estimate the responsibility
[20]. The training of this model can be achieved by an analogous algorithm to the EM called Variational EM (VEM), which, as the EM algorithm, also requires a proper initialisation of the hyperparamters [21]. The optimisation of the variational posterior distribution can also be split into two steps: the E step, where the current distributions over the model parameters are used to estimate the responsibility 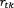 of the component k for generating the data point t, and the M step, where
of the component k for generating the data point t, and the M step, where 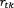 is used to re-estimate the parameters of the observed data
is used to re-estimate the parameters of the observed data 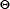 , analogously to the conventional EM algorithm, and the new hyperparameters of the Dirichlet and Gaussian-Wishart distributions. The re-estimation formula's for the hyperparameters are given by (see Eqs. (18-22)) [14]:
, analogously to the conventional EM algorithm, and the new hyperparameters of the Dirichlet and Gaussian-Wishart distributions. The re-estimation formula's for the hyperparameters are given by (see Eqs. (18-22)) [14]:
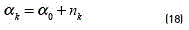
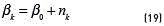
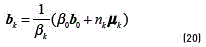
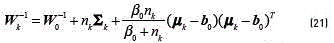
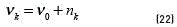
where 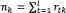 . For some observation x, the predictive distribution of this Bayessian model can be approximated as a mixture of Students t-distributions given by (see Eqs. (23) and (24)) [14]:
. For some observation x, the predictive distribution of this Bayessian model can be approximated as a mixture of Students t-distributions given by (see Eqs. (23) and (24)) [14]:
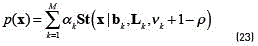
where the precision is given by
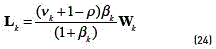
According to [14], when the size of the data set is large, the predictive distribution Eq. (23) reduces to a mixture of Gaussians. Given an observation Ot, the predictive distribution obtained from Eq. (23), can be used to estimate the responsibility of each component (similar to Eq. (12)) as (see Eq. (25)):
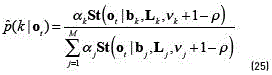
Using this responsibility and the re-estimation formula's for the k-th component of the M step in the VEM algorithm given by (see Eqs. (26) and (27)):
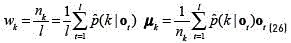
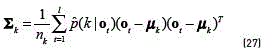
it is possible to estimate the parameters of a conventional UBM. Furthermore, from it, any of the two former strategies and/or adaptations can be applied [22].
3. Experiments and results
3.1. Database
The data set used for the experiments was the MCYT100 Signature sub-corpus, which contains 25 client signatures and 25 highly skilled forgeries (with natural dynamics) from 100 signers. Both, on-line information (pen trajectory, pen pressure and pen azimuth=altitude), and off-line information (image of the written signature) are included in the database. Nevertheless, in this work only the on-line part of the database was used. By considering the total number of signers and signatures, the number of available samples for simulation are 100 x (25 + 25) = 5000 [23].
3.2. Experimental setup
All the experiments were performed using a bootstrapping validation methodology, with ten repetitions. The size of training and testing subsets were adjusted from 90%-10% to 20%-80% respectively, in order to evaluate the sensitivity of the methods to the number of training samples, and to simulate more real operation conditions. It is worth noting that there are 25 genuine signatures per client in the database, therefore, 90%-10% and 20%-80% corresponds to 22 - 3 and 5 - 20 signatures respectively. Samples used during training are not involved in testing.
Three different experiments were performed: in the first one, genuine and impostor signatures per user were used for training two different models (following each of the strategies exposed in Section 2.2); the decision was taken by estimating the likelihood ratio (Eq. (6)) and comparing it with respect to the Equal Error Rate (EER) decision threshold. This is an unrealistic scenario because it uses the impostor samples during training, but it is used here only for comparison purposes. In the next experiments, the genuine signatures from all the users were used to train a UBM model, from which genuine models per user were adapted. The validation was performed using genuine signatures from other signers (random forgeries - called experiment 2) and impostor samples (skilled forgeries - called experiment 3). The likelihood ratio in this case was estimated between the genuine model and the UBM, and also comparing it against the EER threshold. The number of Gaussians for the UBM model was evaluated in the range between 5 and 20. The kernel function for the SVM based model was a Radial Base Function (RBF) and the regularisation and kernel parameters were set during validation. The results are presented in terms of false acceptance rate (FAR), false rejection rate (FRR) and EER, along with the area under the Receiver Operator Characteristic curve (AUC) and Detection Error Trade-off (DET) plots.
3.3. Results
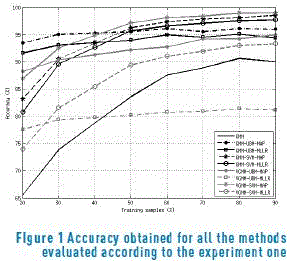
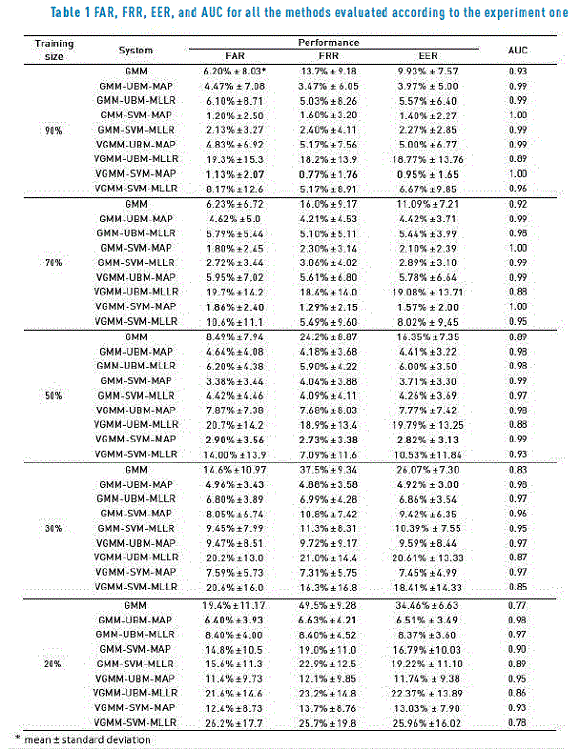
Table 1 shows the results for all the models and strategies described in Section 2.2, according to the experiment one. It is possible to observe how the performance of the models degrades with respect to a reduction in the number of training samples. However, it is worth to highlight that the system based on GMM-UBMMAP method was able to keep the accuracy above 93%, even when only 20% of the samples were used for training. The accuracy obtained by the GMM-SVM models, is considerable better than the GMM-UBM models when the available training subset is at least 50% of the whole database (corresponding to 13 signatures). When 90% of the samples were used for training, the relative reduction of the recognition rate using the GMM-SVM model is of 35.26% (2.57% in absolute terms). On the contrary, the performance of GMM-SVM models degrades faster for the experiments with 40% or less training data. The best result is achieved by the combination of the variational learning of UBM, along with a MAP adaptation and a SVM supervector classifier. This scheme yields to a recognition rate above 99% when the training included more than 80% of the samples. However, similar to the GMM-SVM models, its performance degrades quite fast with 40% or less training data. This could be explained because even though the training of the UBM is carried out using a full Bayesian method, this scheme requires two different adaptations, which demand enough data. It is worth to note that in this context the MAP adaptation always provided better results than the MLLR.
Figure 1 shows the accuracy obtained by all the methods evaluated according to the experiment one. As it was pointed out above, the best result was achieved by the combination of a variational GMM with a SVM, through a MAP adaptation, which following the notation in [11], could be called a Variational GMM-Supervector. Nevertheless, the standard GMM-UBM model was the most stable with respect to the size of the training subset. Anyway, all the models based on a UBM were better than the conventional GMM for small training sets.
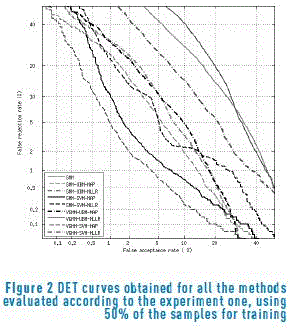
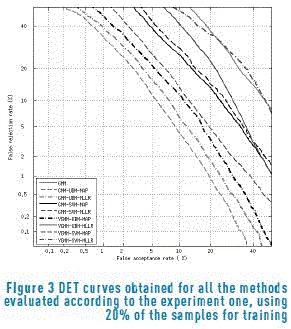
Figures 2 and 3 show the DET curves for all the methods evaluated according to the experiment one, using 50% and 20% of the samples for training respectively.
Table 2 shows the results for all the models according to the experiment two. This is a more realistic scenario in which there is not available impostor samples during the training stage. It is of course, a more difficult challenge for the system. As it was pointed out before, during the experiment two the system is tested using the validation subset of one genuine signer (positive class) against the validation set of all other signers (negative class). This process is repeated for all the signers in the database. Therefore, there are much more samples in the negative class than in the positive one. For instance, in the experiment 20%-80%, the model of every signer is tested using 20 genuine and 1980 impostor signatures. Bearing this in mind, it is possible to observe that several of the evaluated models were able to detect perfectly impostor signatures. Actually, the models based on GMM-SVM-MAP and VGMM-SVM-MAP, were able to detect all the impostor signatures even when only 20% of the samples were used for training. On the other hand, it is also possible to observe that as long as the number of training samples decreases, the system becomes more and more biased to the general class represented by the UBM. This fact is even more evident for systems using the combination of GMM and SVM models, whilst FAR remains in low rates, FRR increases to very high levels. This fact can be explained because during training, the samples used as positive class correspond to the genuine samples from one user, while the negative class is formed by the genuine samples from all other users in the database. This configuration produces an unbalanced training set that skews the system to the class with more data, reducing false positives and increasing false negatives. Although the percentage of training samples is reduced in the same proportion for both classes, this behaviour becomes more evident as the percentage of the training data is reduced because the number of genuine samples reaches critical values. Nevertheless, it is worth noting that the FRR obtained by VGMM-SVM-MAP during the experiment 20%-80% (38.2%) equates to 7.6 samples, i.e. the system made, on average, 7.6 mistakes every 2000 validations. Moreover, although the aim is to get a system with FAR and FRR as low as possible, in the context of biometric verification systems is most important do not give access to impostor people (i.e. to achieve a low FAR), than to commit some errors with genuine users (i.e. to achieve a low FRR), which would be asked to perform a new verification.
From Table 2, it is also possible to observe clearly, the superiority of the system based on the variational GMM-supervector. It is important to note that, for almost all the models, the performance degrades faster when the training set included less than 50% of the samples (around 12 signatures per user), which could be explained by the intrinsic variability among the signatures patterns from a single user, preventing the system to capture enough discriminative information from very small data sets. Anyway, the combination of a full Bayesian UBM and a SVM, was able to achieve more than 99.6% of accuracy using only 5 samples for training, and 99.8% when 12 signatures were used instead.
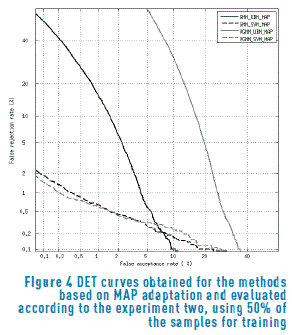
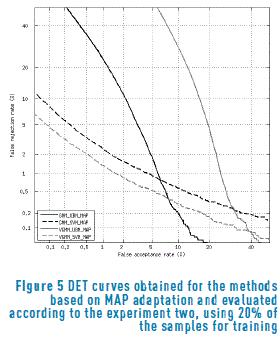
Figures 4 and 5 show the DET curves for the methods evaluated according to the experiment two, using
50% and 20% of the samples for training respectively. Only the models based on MAP adaptation were included, since in all the cases MAP beats MLLR. From these figures, it is possible to observe that for 50% of the training samples, the performance of the GMM-SVM-MAP method is quite similar to the variational version of the same scheme. However, for 20% of training samples, there is a greater difference between these two methods, confirming that the Bayesian approach is more suitable for small-sample conditions.
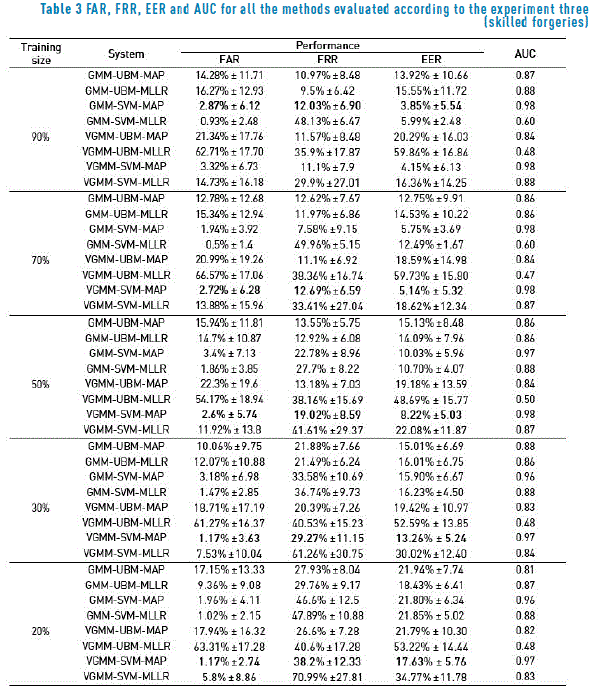
Table 3 shows the results for all the models according to the experiment three. This is the same system that in the experiment two but tested using the impostor samples per user. In this case, the imbalance is not as strong as in the former case, since in every repetition there are only 25 negative samples (the total number of impostor signatures per client in the database). Therefore, in this case the positive samples wrongly classified have more weight on the global error (we are aware that other performance measures such as the geometric mean or the probability excess are less sensitive to the relative class frequency in the test set. However, those kind of measures are not commonly used in the context of signature verification, so they cannot be used for comparison purposes. Anyway, since those kind of measures are usually estimated from sensitivity and specificity measures, they can be easily estimated from the FAR and FRR values provided in the tables if needed). The best performance was obtained by a system based on a GMM-UBM model with MAP adaptation, achieving on average, an error of 3.85% when the 90% of the samples were used for training. During the experiment 20%-80%, the best performance was obtained by the variational GMM-supervector. In this case, the FAR increases up to 1.17% in comparison to the 0.0% achieved in the former experiment. This means that on average, for every 100 validations with impostors signatures, the system accepted as genuine one. On the other hand, in this experiment the positive samples are the same than in the previous one, so the FRR values are exactly the same than in Table 2.
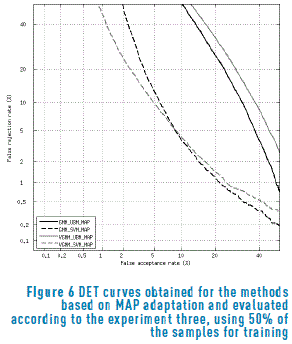
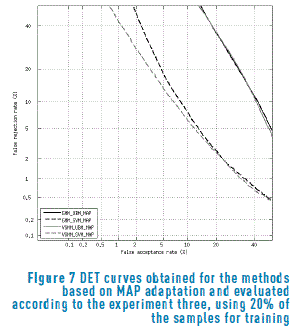
Figures 6 and 7 show the DET curves for the methods evaluated according to the experiment three, using 50% and 20% of the samples for training respectively. Once again, only the models based on MAP adaptation were included. Unlike the previous experiment, in this case the performance of the GMM-SVM-MAP and VGMM-SVM-MAP remain similar even during the experiment 20%-80%, with a slightly improvement of the variational method when the training samples were reduced up to 5 (20%).
3.4. Discussion
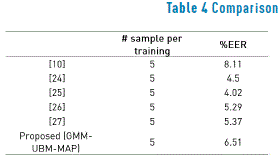
A comparison of the performance of different signature verification systems is a difficult task since each author constructs his own signature data-sets. The lack of a standard international signature database continues to be a major problem for performance comparison. For the sake of completeness, in Table 4 we present some results obtained by published studies that used the MCYT database. Although it is not possible to carry out a direct comparison of the results, since the methodologies of training and testing and the classification strategies used by each author are different, Table 4 enables one to visualise results from the proposed methodology along side results published by other authors. It is worth to highlight that, most of the papers include some percentage of impostor samples into the training set, whilst in our experiments, assuming that in more realistic conditions there are not impostor samples available, impostor samples were only used during testing. Results presented here could be considered acceptable, taking into consideration that only raw data (i.e. velocity, acceleration) were used to feed the classifier, while most of the papers use more advanced characterisation strategies. In the present work, the main aim is to test the generalization capabilities of the Bayesian learning techniques, presented in section 2.2, in the context of on-line signature verification; nevertheless, the next step is to combine this kind of learning techniques with more robust characterisation strategies, for which more direct comparisons can be made.
4. Conclusion
The paper evaluates nine different strategies based on Gaussian Mixture Models in the on-line signature verification task. All the models were tested under different conditions of available training samples and three different experiments including skilled forgeries during training and testing, and only in testing.
For almost all the methods evaluated, the performance degrades faster when the training set included less than 50% of the samples (around 12 signatures per user), which can be explained by the intrinsic variability among the signature patterns from a single user, preventing the system to capture enough discriminative information from very small data sets. However, for the genuine vs. impostor experiment, the GMM-UBM model was able to keep the equal error rate around 6% even when only 5 signatures per user were used in the training set. However, efforts to enhance feature extraction should be made.
In almost all the cases, the VGMM-UBM-SVM, was the model with the best performance, confirming that the Bayesian learning is more suitable for small-sample size conditions. This model was able to keep the false acceptation rate lower than 3% using only 5 signatures per used for training, and without any information about skilled forgeries. Moreover, when the system was tested against an impostor claiming to be another user but tracing his own signature, the system based on the combination of GMM-SVM, either using EM or Variational EM, achieved FARs equal to 0%, even for 20% of training samples, i.e. the systems rejected all the impostors without fail.
For all the experiments, the performance of MAP adaptation was by far better than the MLLR one. The combination of the classification strategies based on GMM-SVM and VGMM-SVM, with more advanced characterisation methods, should be the next step to figure out the real potential of these methods in the on-line signature verification task.
5. Acknowledgment
This research was supported by the project No. 111556933858 funded by COLCIENCIAS.
6. References
1. S. Liu and M. Silverman, ''A practical guide to biometric security technology'', IT Professional, vol. 3, no. 1, pp. 27-32, 2001. [ Links ]
2. K. Franke and J. Ruiz, ''Soft-biometrics: Soft-computing technologies for biometric-applications'', in AFSS International Conference on Fuzzy Systems, Calcutta, India, 2002, pp. 171-177. [ Links ]
3. S. Impedovo and G. Pirlo, ''Verification of handwritten signatures: An overview'', in 14th International Conference on Image Analysis and Processing (ICIAP), Modena, Italy, 2007, pp. 191-196. [ Links ]
4. J. Vargas, M. Ferrer, C. Travieso and J. Alonso, ''Off-line signature verification based on grey level information using texture features'', Pattern Recognition, vol. 44, no. 2, pp. 375-385, 2011. [ Links ]
5. M. Malekar and S. Patel, ''Off-line signature verification using artificial neural network'', International Journal of Emerging Technology and Advanced Engineering, vol. 3, no. 9, pp. 127-130, 2013. [ Links ]
6. M. Kumar, ''Signature verification using neural network'', International Journal on Computer Science and Engineering, vol. 4, no. 9, pp. 1498-1504, 2012. [ Links ]
7. E. Argones and J. Alba, ''Online signature verification based on generative models'', IEEE Transactions on Systems, Man, and Cybernetics, Part B, vol. 42, no. 4, pp. 1231-1242, 2012. [ Links ]
8. D. Reynolds, T. Quatieri and R. Dunn, ''Speaker verification using adapted Gaussian Mixture Models'', Digital Signal Processing, vol. 10, no. 1-3, pp. 19-41, 2000. [ Links ]
9. L. Wan and B. Wan, ''On-line signature verification with two-stage statistical models'', in 8th International Conference on Document Analysis and Recognition (ICDAR), Seoul, South Korea, 2005, pp. 282-286. [ Links ]
10. M. Martinez, J. Fierrez and J. Ortega, ''Universal background models for dynamic signature verification'', in 1st IEEE International Conference on Biometrics: Theory, Applications, and Systems (BTAS), Crystal City, USA, 2007, pp. 1-6. [ Links ]
11. W. Campbell, D. Sturim and D. Reynolds, ''Support vector machines using GMM supervectors for speaker verification'', IEEE Signal Processing Letters, vol. 13, no. 5, pp. 308-311, 2006. [ Links ]
12. H. Attias, ''Inferring parameters and structure of latent variable models by variational Bayes'', in 15th Conference on Uncertainty in Artificial Intelligence, Stockholm, Sweden, 1999, pp. 21-30. [ Links ]
13. S. García, J. Luengo and F. Herrera, Data Preprocessing in Data Mining, 1st ed. New York, USA: Springer, 2015. [ Links ]
14. C. Bishop, Pattern Recognition and Machine Learning, 1st ed. New York, USA: Springer, 2006. [ Links ]
15. D. Reynolds, ''Speaker identification and verification using Gaussian mixture speaker models'', Speech Communication, vol. 17, no. 1-2, pp. 91-108, 1995. [ Links ]
16. R. Duda, P. Hart and D. Stork, Pattern classification, 2nd ed. New Jersey, USA: Wiley-Interscience, 2000. [ Links ]
17. M. Ferras, L. Cheung, C. Barras and J. Gauvain, ''Comparison of speaker adaptation methods as feature extraction for SVM-based speaker recognition'', IEEE Transactions on Audio, Speech, and Language Processing, vol. 18, no. 6, pp. 1366-1378, 2010. [ Links ]
18. C. Leggetter and P. Woodland, ''Maximum likelihood liner regression for speaker adaptation of continuous density hidden Markov models'', Computer Speech and Language, vol. 9, no. 2, pp. 171-185, 1995. [ Links ]
19. C. Cortes and V. Vapnik, ''Support-vector networks'', Machine Learning, vol. 20, no. 3, pp. 273-297, 1995. [ Links ]
20. K. Murphy, Machine Learning: A Probabilistic Perspective, 1st ed. Cambridge, USA: MIT Press, 2012. [ Links ]
21. N. Nasios and A. Bors, ''Variational learning for Gaussian Mixture Models'', IEEE Trans. Systems, Man, Cybern., Part B, vol. 36, no. 4, pp. 849-862, 2006. [ Links ]
22. V. Sahu, H. Mishra and C. Shekar, ''Variational bayes adapted GMM based for audio clip classification models'', in 3rd Int. Conf. Pattern Recognition Mach. Intell., New Delhi, India, 2009, pp. 513-518. [ Links ]
23. J. Fierrez, J. Ortega, D. Torre and J. Gonzalez, ''Biosec baseline corpus: A multimodal biometric database'', Pattern Recognition, vol. 40, no. 4, pp. 1389-1392, 2007. [ Links ]
24. J. Montalvao, N. Houmani and B. Dorizzi, ''Comparing GMM and parzen in automatic signature recognition a step backward or forward'', in XVIII Brazilian Congress on Automatics, Bonito, Brazil, 2010, pp. 4463-4468. [ Links ]
25. N. Sae and N. Memon, ''Online signature verification on mobile devices'', IEEE Transactions on Information Forensics and Security, vol. 9, no. 6, pp. 933-947, 2014. [ Links ]
26. J. Fierrez, L. Nanni, J. López, J. Ortega and D. Maltoni, ''An on-line signature verification system based on fusion of local and global information'', in 5th International Conference on Audio- and Video-Based Biometric Person Authentication (AVBPA), Hilton Rye Town, NY, USA, 2005, pp. 523-532. [ Links ]
27. S. Garcia et al., ''Online Handwritten Signature Verification'', in Guide to Biometric Reference Systems and Performance Evaluation, 1st ed. D. Petrovska, G. Chollet and B. Dorizzi (eds). New York, USA: Springer, 2008, pp. 125-165. [ Links ]