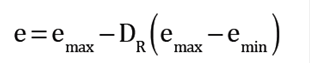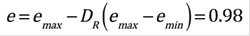1. Introduction
Blast densification is a common technique used to densify large areas of potentially liquefiable stratum, and thus, to prevent or mitigate the effects of earthquake-induced liquefaction and flow. The main limitation of this technique is that the design is largely empirical and there is not a well-established theoretical procedure available to conduct the design of a blasting program, and to estimate the number of passes needed to achieve a target density 1. Therefore, a rational procedure is needed to define and confirm how much improvement is required to meet the design objective of a particular project.
Blast densification consists on placing explosives throughout the layer requiring treatment, and then detonate them with multiple delays to generate a cyclic load. The high pressure wave breaks any interparticle bonds due to cementation and increases the pore fluid pressure. As the excess pore fluid pressure increases, the confining effective stresses decrease to zero and liquefaction is triggered. After liquefaction and as the induced pore fluid pressure dissipates, the soil reconsolidates to a denser state and the confining effective stresses return to the pre-blast values. Depending on the grain size distribution, initial density of the sand and the blast densification program, vertical axial strains up to 4 % can be achieved in a single pass 2. Further compaction can be achieved by implementing several passes 2)(3)(4)(5.
This paper proposes a methodology, based on the critical state concepts, to quantify the amount of densification or number of passes required to make the soil resistant to liquefaction and flow in the presence of shear stresses. This methodology provides engineers with a rational way to estimate how much improvement is required in the soil to meet the design objective of a particular project and the costs associated with it. The effects of gas, released and trapped during blasting, on the mechanical response of the soil are not considered in this paper. However, further details can be found in 2.
2. Mechanism during blast densification
One of the most accepted methods for defining whether or not a saturated granular soil will liquefy and flow is embodied in the concepts of the critical state soil mechanics. The critical state line (CSL) represents the relationship between the critical void ratio and effective stresses when a soil has failed 6. The soil response to monotonic or dynamic loads strongly depends on the mean normal effective stress, p’, and void ratio, e. This is illustrated on the state diagram shown in Figure 1. For example, a sample with an initial state above the CSL will tend to contract and develop positive excess pore water pressure when subjected to undrained loading until no further changes in effective stress occur. On the other hand, a sample in an initial state below the CSL will tend to dilate and develop negative pore water pressure, increasing the effective stresses until the critical state line is reached.
After each blast event, the excess pore water pressure rapidly builds up, decreasing the confining effective stresses to zero and triggering a condition of initial liquefaction. As the blast-induced pore pressure dissipates, the effective stresses will increase and a reduction in the soil void ratio [ in Figure 1(b)], will occur. Conceptually, no more blast densification is needed once the soil void ratio is below the critical state line [point A’ - Figure 1(b)] because, at this state, a dilative behavior is expected. However, further densification may be needed to account for extra stresses, ∆p, induced by the facility or embankment to be constructed, as noted by point B. If the embankment stresses are large enough to change the soil state to above the critical state line, and hence be loose of critical, it will be again susceptible to liquefaction and flow.
in Figure 1(b)], will occur. Conceptually, no more blast densification is needed once the soil void ratio is below the critical state line [point A’ - Figure 1(b)] because, at this state, a dilative behavior is expected. However, further densification may be needed to account for extra stresses, ∆p, induced by the facility or embankment to be constructed, as noted by point B. If the embankment stresses are large enough to change the soil state to above the critical state line, and hence be loose of critical, it will be again susceptible to liquefaction and flow.
3. Proposed methodology to quantify amount of densification
Figure 2 illustrates the proposed method for estimating the expected volume change during reconsolidation from a zero effective vertical stresses to the in-situ vertical stresses. The sketch shows the results of constrained compression tests on specimens initially prepared at two different dry densities, ρd1 and ρd2.
Point A represents the initial state of the sand in the ground. If the blast is large enough to liquefy the soil, and assuming that no volume change occurs during blasting (a good approximation for the very rapid loading resulting from a blast event), the state of the soil element will move to point A’. As the induced pore water pressure dissipates, the soil will reconsolidate along path A’-B, resulting in a void ratio change of Δe1. A second blast will cause the soil element B to move to point B’ (if liquefaction is induced) and will reconsolidate along path B’-C.
A similar trend is assumed for the subsequent blasts. In this manner, the volume changes measured in the laboratory can be used to predict the volume changes in the field after each blast event. For this purpose, a family of e− 𝜎 𝑣 ′ curves, similar to those shown in Figure 2, can be determined for values of ρ d and effective stress conditions expected during the blasting program.
This approach assumes that the densification of a loose deposit is a direct consequence of the blast induced pore water pressure dissipation and soil re-sedimentation, and that no soil volume change will occur during blasting due to the very rapid loading resulting from each blast event. Also, it is assumed that the soil experiences a one-dimensional (1D) consolidation process and thus, 1D constrained compression tests (oedometer tests) could provide a clear indication of the amount of densification that the soil mass will experience after each blast. These assumptions are representative of the soil behavior during and after blasting 2)(3)(5)(7).
3.1. Steps proposed to determine the number of passes for a given project
The following steps are proposed to quantify the amount of densification required to prevent liquefaction and flow for a given project.
Step 1. Identify the potentially liquefiable layers
Field penetration tests such as the cone penetration test and the standard penetration test can be used to determine the soil stratigraphy, and to identify loose sands and silty sands deposits below the groundwater table that are susceptible to liquefaction and flow. The advantage of the cone penetration test over the standard penetration test is that a continuous profile for stratigraphic interpretation is developed and the test results are more consistent and repeatable 8. The procedure presented by 8, in chapter 10, can be used to identify the soils that are prone to liquefaction and flow.
Step 2. Characterize the material collected from the loose layer
A complete geotechnical testing program should be conducted on the collected sand sample to evaluate its index properties. The laboratory program should be conducted according to the ASTM specifications and include the visual classification test, sieve analysis test [(9) & (10)], specific gravity test [(11)], and maximum and minimum densities tests [(12) & (13)].
Step 3. Estimate the initial in-situ void ratio
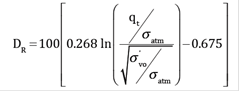
It is important to accurately measure the in-situ void ratio of the liquefiable layers before blasting. This parameter is needed to evaluate the soil liquefaction potential and to estimate the amount of densification needed at a particular project. The in-situ void ratio can be reliably measured by recovering undisturbed samples from the loose sand layer. However, for most practical cases, the cost of this alternative is large and almost prohibited. 8 presents a relationship that can be used to infer the in-situ void ratio from the cone penetration resistance test. This relationship was developed for clean sands with less than 15% fines content. The relative density and in-situ void ratio are computed as presented in Eqs. (1) and (2), respectively.
where D R is the relative density in percentage, q t is the corrected tip cone penetration resistance, σ atm is the atmospheric pressure (1 atm =1 bar = 100 kPa) and σ vo ′ is the initial effective vertical stress. e min and e max are the minimum and maximum void ratios respectively, determined as explained in step 2.
Step 4. Determine the critical state line
The position of the critical state line (CSL) is determined by conducting undrained triaxial compression tests on five or six reconstituted saturated specimens of identical soil. In order to ensure a fully contractive response and that the critical state line can be determine reliably, the samples should be consolidated to stresses higher than the critical state values at a given void ratio. The CSL must be defined over a range of void ratios and stresses representative of those in-situ values.
Step 5. Determine the expected void ratio change as function of the dry density
A series of one-dimensional constrained compression tests on dry samples are prepared at various dry densities representative of those densities expected in the field before and after blasting. Follow the procedure presented herein to estimate the void ratio change as function of dry density. These results represent well the behavior of saturated soil because they are function of maximum and minimum void ratio as well as the dry density.
Step 6. Compute the number of blast events needed to achieve the design objective
The amount of densification or the number of blast events required to prevent liquefaction in a given project will depend on the amount of axial deformation that the soil mass will be allowed to experience during an earthquake. Although a soil with a state of stresses below but close to the critical state line is not susceptible to liquefaction and flow, excessive axial deformations can occur during cyclic loading. Therefore, it is recommended to further densify the soil to ensure a fully dilative response, and to account for the load increment induced by the structures constructed above the soil.
Figure 3 illustrates the procedure proposed in this step. The first stage consists of estimating the void ratio change that will occur after each one of four or five blast events. These void ratio changes are computed from the results obtained in step 5. The second stage consists of conducting a cyclic triaxial test on a reconstituted saturated sample, at each estimated void ratio. The cyclic stress ratio applied to the samples must be representative of that of the expected earthquake. The third stage consists of quantifying the number of blast events. For practical purposes, the number of passes needed in a given project will correspond to that of the void ratio where the axial strain developed during cyclic loading is acceptable for the project in question.
3.2. Example calculation - number of blast events needed at a sanitary landfill (Oakridge landfill)
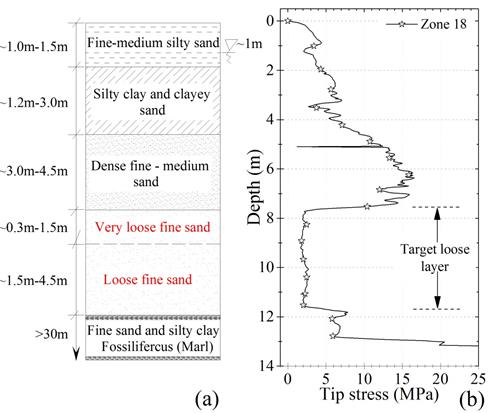
This example presents the step-by-step procedure proposed to estimate the number of passes needed to prevent liquefaction and excessive axial deformations at a sanitary landfill located in South Carolina, USA. A more detailed description of this site can be found in 2. The soil profile at the site is composed of six distinctive layers (Figure 4). Starting at the ground surface, the soil consists of (i) 1.0 m to 1.5 m fine-medium silty sand; (ii) 1.2 m to 3.0 m of silty clay and clayey sand; (iii) 3.0 m to 4.5 m of dense fine to medium sand; (iv) 0.3 m to 1.5 m of very loose fine sand; (v) 1.5 m to 4.5 m of loose fine sand; and (vi) more than 30 m of a fine sand and silty clay layer 3)(7. The water table is located between 0.8 - 1.5 m below the ground surface.
Step 1:Figure 4 shows a typical CPT sounding performed at the site before blasting. The loose sand layer susceptible to liquefaction and flow was found at a depth between 7.6m and 11.5m. The average thickness of the liquefiable layer in these zones was 4.0 m.
Step 2: A laboratory program was implemented to characterize the sand samples collected from the target loose layer during the blast densification program. The soil is a clean, fine grained sand, SP, angular in shape, with little fines. The average uniformity coefficient ( C u ) and curvature coefficient ( C c ) were 1.63 and 1.03, respectively, and the minimum and maximum void ratios were emin = 0.62 and emax = 1.04, respectively. The percentage of fines passing sieve # 200 was approximately 1.5% and 7% by weight when the dry and wet sieve analysis were conducted, respectively. The specific gravity value is 2.66.
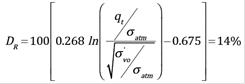
Step 3: In average, the tip cone penetration resistance for these zones is 𝑞 𝑡 = 2.1 MPa (Figure 4). The effective vertical stress acting at the middle of the loose sand layer is approximately 𝜎 𝑣𝑜 ′ = 100 kPa. From Eqs. (1) and (2), the initial in-situ relative density and void ratio inferred from the CPT soundings are computed as presented in Eqs. (3) and (4), respectively.
Step 4: Five undrained triaxial compression tests were performed to determine the critical state line (Figure 5). The critical state void ratio, at an effective mean normal stress of 100 kPa, is estimated to be between 0.83 and 0.84.
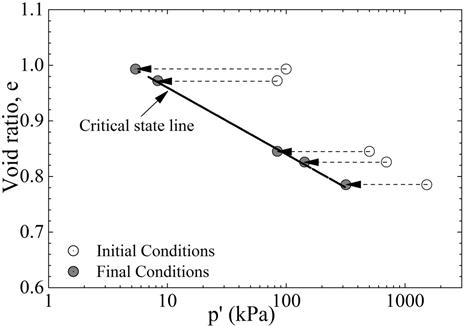
Step 5: Twenty-one one-dimensional constrained compression tests were conducted on dry samples prepared at various densities to estimate the expected void ratio change that will occur after each blast event. Figure 6 shows the results from oedometer tests conducted on the collected sand samples.
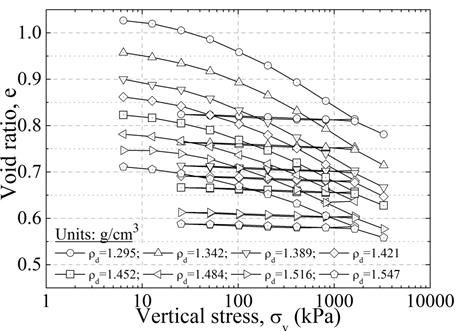
Figure 7 shows an illustrative example of how to compute the expected void ratio change after each blast event. In this figure, it is assumed that there is no void ratio change from σ v ′ =0kPa to σ v ′ =6 kPa (first load increment to ensure contact between the soil and the loading plate). Assuming that the void ratio and in-situ vertical stress acting on the loose sand before blasting are 1.05 and 100 kPa, respectively, the first blast will reduce σ v ′ to 0 kPa and the soil will reconsolidate along path a-a’, resulting in a void ratio change of 0.073. A second blast will reduce σ v ′ to 0 kPa and will cause the soil to reconsolidate along the path b-b’, resulting in a void ratio change of 0.067. The same procedure can be followed to compute the expected volume changes for subsequent blasts.
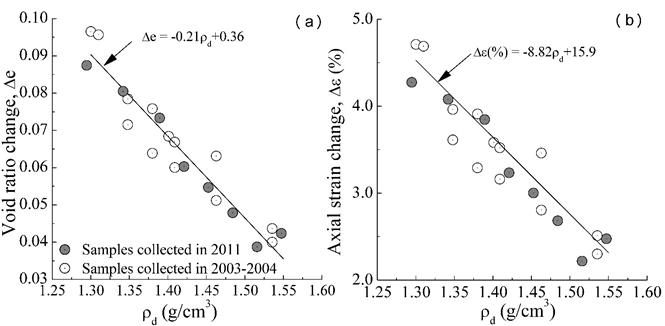
At the Oakridge landfill site, the expected void ratio and axial strain changes can be expressed in terms of the dry density before each blast event as shown in Figure 8.
Step 6: The subsequent change in void ratio associated to each blast event is estimated from Figure 8. Once the post-blast in-situ void ratio is determined, the relative and dry densities of the soil can be computed. Then, an estimation of the ∆𝑒 to a subsequent blast can be estimated from Figure 8(a).
The in-situ void ratio before blasting was estimated to be 0.98. The final void ratio after the first, second, third and fourth blast event are approximately 0.90, 0.83, 0.78 and 0.73, respectively (Figure 8). These void ratios and axial strain changes correspond to relative densities of 35%, 50%, 63% and 74%, respectively. 2 presents the cyclic response of saturated tests conducted on sand samples collected in zone 18 and consolidated to an average void ratio of 0.82, 0.78 and 0.70, respectively and subjected to a cyclic stress ratio of 0.15 [Figures 6-21 to 6-23 in ref. 2]. These results showed that even though liquefaction and flow did not occur, the samples with eaver.=0.82 and eaver.=0.78 experienced considerable axial deformations (i.e., ε a =5% after 49 cycles for eaver.=0.78). For the case of the Oakridge Landfill site, four blast events are considered enough to significantly decrease the soil liquefaction potential and to prevent excessive axial strains from developing during an earthquake 2)(5.
4. Summary and conclusions
A step-by-step procedure is proposed to quantify the number of passes needed to bring the improved soil to a state of stresses below, but further away, of the critical state line, where a dilative response is expected and the soil is no longer considered susceptible to liquefaction and flow.
The laboratory experimental program must be conducted so that the tested specimens are representative of the initial and final range of stresses and void ratios expected at the field during blasting.
For the case history presented herein, Oakridge Sanitary Landfill, the critical void ratio at a mean normal stress of 100 kPa is 0.82 (Figure 5). The calculated void ratio after the third blast event is 0.78, and corresponds to a relative density of 63 % (step 6). The results show that three passes are enough to bring the soil state of stresses below the critical state line, and thus prevent liquefaction and flow. However, further passes must be required depending on the allowable axial strain criteria for a given project.
The proposed methodology could provide to engineers a rational manner to estimate how much improvement is required to meet the design objective of a particular project and the costs associated with it.
5. Acknowledgement
Financial support for the first author was provided by the Infrastructure Technology Institute (ITI) of Northwestern University and the National Science Foundation. The laboratory test results used for the sample calculation were carried out at Northwestern University while the first author was a graduate research assistant in the Department of Civil and Environmental Engineering. The author wishes to thank Dr. Richard Finno, professor at Northwestern University, for his valuable comments and encouragement.