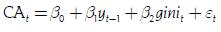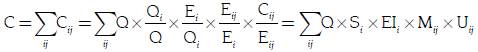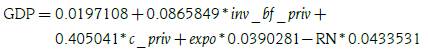INTRODUCCIÓN
La degradación ambiental es uno de los problemas complejos de la humanidad que resulta prioritario resolver debido a sus efectos en la salud de la población y en el ecosistema, que pueden a su vez, conllevar cambios radicales en las actividades del ser humano. Por ello, la ciencia económica debe plantear alternativas de solución con un enfoque sistémico y prospectivo. Este artículo analiza el problema de la degradación ambiental desde una perspectiva sistémica mediante el uso de mapas de influencia y el diagrama de Forrester, los cuales se complementan con herramientas econométricas.
La curva medio ambiental de Kuznets (CMK) supone un primer intento por abordar el problema de la degradación ambiental. El análisis de los efectos de los múltiples contaminantes en el Producto Interno Bruto (PIB) per cápita permitiría identificar qué actividades económicas generadoras de determinados contaminantes requieren mayor regulación ambiental. En un abordaje más detallado, se describen luego las complejas relaciones entre la economía y el medio ambiente y las causas estructurales que provocan su comportamiento. Para ello, se modela un diagrama de influencias que permite explicar el comportamiento de las variables involucradas en la curva de Kuznets. Posteriormente se aplica el modelo sistémico de Forrester y su simulación dinámica −aquí enfocada en el contaminante dióxido de carbono (CO2)− y se explican sus fuerzas motrices.
Este artículo se sustenta en el análisis sistémico de la degradación ambiental aplicado al caso de Ecuador, que publicaron Robalino, Mena y García (2014). Estos autores desarrollaron un modelo de dinámica de sistemas basado en la identidad propuesta por el economista energético japonés Yoichi Kaya, que relaciona el PIB per cápita, la intensidad energética y la intensidad de carbonización del CO2, y describe la relación que existe entre los factores que influyen en las tendencias relacionadas con la energía y las emisiones de dióxido de carbono que se emiten a la atmósfera (Kaya y Yokorobori, 1997).
El modelo de dinámica de sistemas planteado en este artículo emplea la identidad de Kaya, a la cual se le incorpora el modelo de formación del PIB de la economía peruana y se añade la contribución de la energía renovable, con el fin de investigar la relación entre el crecimiento económico, el consumo de energía y las emisiones de CO2. Este modelo se implementó con la técnica de Forrester y el software Stella. A través de la creación de escenarios, este modelo permite analizar la forma en la que los cambios en los factores de las matrices involucradas afectan las emisiones de CO2.
Este artículo está compuesto por cuatro secciones. Posterior a la introducción, el primer capítulo presenta una revisión de la literatura sobre CMK; en el segundo capítulo se realiza el abordaje econométrico de la CMK para Perú, con seis contaminantes; el tercer capítulo presenta el análisis sistémico de la CMK aplicada al CO2 para Perú; y el cuarto capítulo expone las conclusiones.
1. REVISIÓN DE LITERATURA: LA HIPÓTESIS DE LA CURVA MEDIO AMBIENTAL DE KUZNETS
1.1. Explicaciones teóricas para la existencia de la CMK
De acuerdo con Zilio (2010), la hipótesis de Kuznets tiene relevancia a partir de los estudios de Grossman y Krueger (1991), de Shafik y Bandyopadhyay (1992) y Panayotou (1993), entre otros; señala también que Panayotou introdujo el concepto de curva ambiental de Kuznets, la cual establece una relación en forma de U invertida entre el ingreso y las emisiones de contaminantes. La denominación de CMK se dio por su similitud con la relación que estableció Simón Kuznets entre el crecimiento económico y la desigualdad en la distribución del ingreso en 1955, la cual dio lugar a que se trasladara este concepto a la economía ambiental.
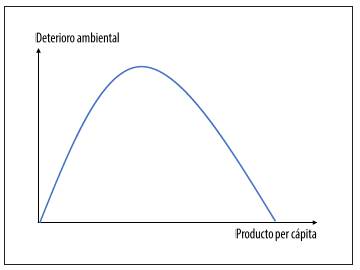
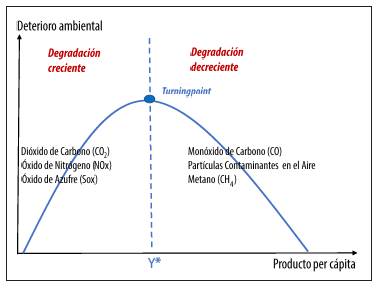
La CMK plantea que el crecimiento económico −medido a través del ingreso o PIB per cápita− y el deterioro ambiental −medido por las emisiones per cápita de algún contaminante− describen una curva en forma de U invertida a largo plazo, lo cual indica que bajos niveles de ingreso se relacionan con un creciente deterioro del medio ambiente, o que el daño ambiental es mayor a medida que aumenta el crecimiento económico. Esta situación se reproduciría hasta alcanzar un punto máximo, llamado nivel crítico de renta o turning point. A partir de este, el nivel de contaminación debería empezat a disminuir y la relación entre las dos variables se tornaría negativa, es decir que mayores niveles de ingreso se asocian a menores niveles de degradación ambiental (figura 1). Esta hipótesis implica que en las primeras etapas de crecimiento de un país (corto plazo) se produce un deterioro ambiental, mientras que, a largo plazo, el crecimiento económico genera mejoras ambientales.
Catalán (2014) señala que esto se debe a que los mayores niveles de desarrollo de una economía implican la transición por diferentes niveles de la estructura productiva: inician en una economía agrícola con un fuerte impacto en la calidad del medio ambiente; pasan por una segunda fase de desarrollo industrial que, a la vez que genera mayor riqueza, ocasiona también mayor daño ambiental; después del turning point, la economía sustenta su crecimiento en tecnologías eficientes y más limpias, sobre todo en el sector de servicios y producción de conocimientos. Según esta hipótesis, los países en vía de desarrollo se ubicarían en la pendiente positiva de la curva, mientras que los países con un desarrollo mayor se encontrarían en la pendiente negativa debido a las políticas de protección del medio ambiente.
Además de la implementación y ejecución de políticas medio ambientales, Falconi, Burbano y Cango (2016) mencionan la importancia de las instituciones para regular los aspectos ambientales. Señalan que el crecimiento económico mejora las capacidades para regular y hacer cumplir la normativa ambiental. Por otro lado, Correa, Vasco y Pérez (2005) resaltan la importancia de las medidas de política que buscan mejorar la distribución del ingreso para lograr resultados medio ambientales positivos más eficientes. Además, Correa (2007) plantea la necesidad de revaluar la hipótesis de la curva CMK, pues en la práctica esta no se cumple, no solo por problemas metodológicos sino por la conceptualización que se le da al término medio ambiente. Señala además que la crítica central a la hipótesis de la CMK, es que las curvas observadas tienen una relevancia limitada por las complejas relaciones entre los ecosistemas y la economía.
Según Zilio (2010), la explicación teórica que sustenta la existencia de esta trayectoria de U invertida consiste en la conjunción de los siguientes efectos en la CMK de las economías en desarrollo (tabla 1).
1. 2. Evidencia empírica sobre la hipótesis de la CMK
A continuación, se presenta la evidencia empírica de la hipótesis de Kuznets a partir del 2005:
Correa, Vasco y Pérez (2005) evaluaron indicadores de contaminación del aire y del agua. Para el caso del dióxido de sulfuro y el humo los resultados muestran una relación en forma de U invertida. En el caso del dióxido de sulfuro, muestran que la relación estimada cambia de tendencia cada vez que se alcanza el mayor nivel de ingresos y se forma una curva en forma de N. Los autores en mención estimaron la CMK para América Latina y el Caribe con una muestra representativa de once países de la región, entre ellos Perú (1980-1997). El estudio se desarrolló para dos contaminantes: CO2 y SO2. Emplearon como variables explicativas: el PIB real per cápita, el coeficiente de Gini, población y tiempo. Concluyeron que detrás de la relación planteada por la CMK entre el ingreso y el deterioro ambiental existen implicaciones en términos de políticas económicas, ambientales y sociales.
Correa (2007) analizó la validez de la CMK para doce países de América Latina (entre ellos Perú). Como variables explicativas utilizó: PIB per cápita, densidad poblacional, derechos políticos y libertades civiles, y el coeficiente de Gini. Los resultados econométricos para emisiones de SO2 muestran una trayectoria de Kuznets para la relación entre este contaminante y el PIB per cápita. Concluyó que, dado que el modelo de Kuznets se restringe a una relación entre contaminación y crecimiento económico, resulta vital una efectiva articulación e implementación de políticas en el ámbito ambiental, social y económico, si es que se busca que estos países alcancen en un menor tiempo la fase decreciente de la curva, sin la necesidad de alcanzar un máximo de contaminación ambiental.
Zilio (2010) aportó evidencia empírica sobre la validez de la curva para veintitrés países de América Latina y el Caribe (entre ellos Perú) de 1970 al 2008. Concluyó que los argumentos presentados no resultan muy operativos en las circunstancias económicas, sociales, e institucionales propias de los diferentes países en desarrollo; indicó que las variables: desigualdad en la distribución del ingreso; y fragilidad del marco institucional en materia ambiental, son las que debilitan los principales fundamentos que sostienen esta hipótesis, con lo cual no se debería esperar un crecimiento económico para alcanzar mejoras en calidad ambiental. Por último, Alonso y González (2017) sugirieron que la hipótesis de Kuznets puede explicar la relación entre crecimiento económico y distribución de ingreso en Colombia, hallaron que el aumento de la población empeora la desigualdad.
2. ABORDAJE ECONOMÉTRICO DE LA CURVA MEDIO AMBIENTAL DE KUZNETS
2.1. Modelo econométrico
Con el fin de medir la relación existente entre el nivel de contaminación, el nivel de ingresos y la desigualdad, se planteó el siguiente modelo econométrico, acorde con Correa, Vasco y Pérez (2005):
Donde:
CA: nivel de contaminación ambiental per cápita en el periodo t
y t-1: PIB per cápita, medido en miles de soles con base en el 2007, en el periodo t-1
gini t: coeficiente de desigualdad de Gini, medido en puntos porcentuales en el periodo t
El CAt considera un set de variables que miden la contaminación per cápita existente en Perú, ámbito nacional:
Dióxido de carbono (CO2), en kilogramos por habitante
Monóxido de carbono (CO), en kilogramos por habitante
Óxido de nitrógeno (NOx), en kilogramos por habitante
Partículas contaminantes en el aire: en kilogramos por habitante
Metano (CH4), en kilogramos por cada 1.000 habitantes
Óxido de azufre (SOx), en kilogramos por habitante
El PIB per cápita y las variables medidoras de la contaminación se obtuvieron del Instituto Nacional de Estadística e Informática (INEI), mientras que el coeficiente de Gini se obtuvo de la base de datos virtual del Banco Mundial (World Bank, 2016), además del documento Evolución Socio Económica del Perú 1990-2010 del Ceplan (2011) 1.
Se eligió el PIB per cápita rezagado porque, según Grossman y Krueger (1995), la respuesta entre los incrementos del ingreso y la mejora o degradación de la calidad del medio ambiente se encuentra retardada por el lapso de ejecución de nuevos proyectos de inversión. Es de especial interés el coeficiente β 1, que evidencia en qué parte de la curva medio ambiental se encuentra el contaminante en Perú. De ser positivo, correspondería al primer estadio y de ser negativo, al segundo. Así mismo, la prueba de quiebre estructural prueba estadísticamente la existencia de algún cambio en la pendiente de la curva medio ambiental.
2.2. Análisis de resultados del modelo econométrico de Kuznets
A continuación, se presenta un consolidado de los resultados:
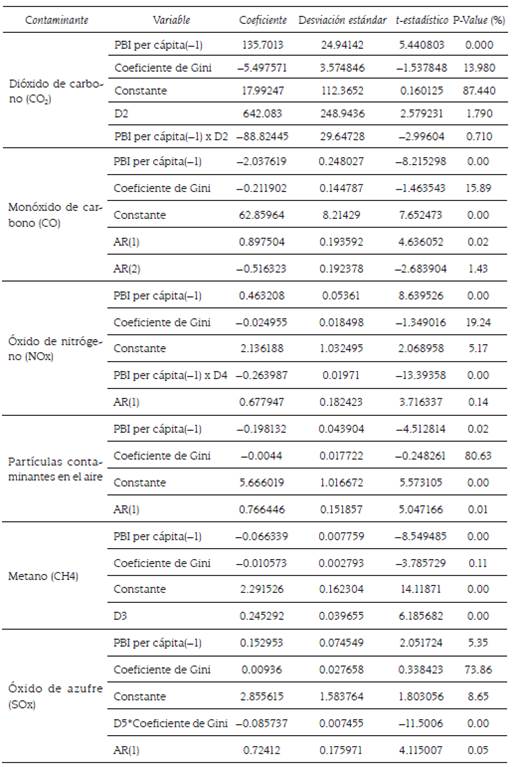
Tabla 2 Resultados de los modelos econométricos para cada uno de los seis contaminantes
Fuente: elaboración propia
De acuerdo con el valor de probabilidad (o nivel de significación) denominado valor-p (p-value), se evidencia que el PIB per cápita es estadísticamente significativo al 1% para los contaminantes dióxido de carbono, monóxido de carbono, óxido de nitrógeno y metano, mientras que para las partículas contaminantes en el aire y para el óxido de azufre lo es, pero al 5% y al 10% de significancia, respectivamente.
Los contaminantes dióxido de carbono, óxido de nitrógeno y óxido de azufre guardan una relación positiva con el nivel per cápita del ingreso o PIB (expresado por el signo del coeficiente), con lo cual se evidencia que se encuentran presentes en la primera etapa de la curva de Kuznets, con lo que, de producirse una mejora en el nivel del PIB, se incrementará a su vez la emisión de este contaminante. Para el CO2, por ejemplo, si el PIB aumenta en una unidad, la contaminación incrementaría 136 veces aproximadamente.
El coeficiente del PIB per cápita es negativo para el monóxido de carbono, las partículas contaminantes en el aire y el metano, por lo tanto, se encuentran en la segunda etapa de la curva de Kuznets, en la que la mejora en el nivel de ingreso per cápita reduce la emisión del contaminante.
De acuerdo con la prueba de quiebre estructural de Quandt-Andrews, existe un quiebre significativo en la tendencia del coeficiente del PIB per cápita para el dióxido de carbono en el 2001, representado por el cambio en el coeficiente del PIB per cápita, que pasó de 135,7013 a 46,87685 (de ahí que el valor del PIB per cápita (-1) x D2 resulte -88,82445). Esta reducción en el coeficiente evidencia una reducción de la pendiente de la CMK, sin embargo, aún permanece en la primera fase. Para los demás casos, la prueba de quiebre estructural no arrojó ningún quiebre significativo, por tanto, los coeficientes de las variables se mantuvieron estables y no se evidenciaron cambios en la pendiente de la curva. Para el óxido de nitrógeno existe un quiebre en la tendencia para el coeficiente del PIB per cápita en el 2011, momento en el cual el coeficiente disminuye de 0,463208 a 0,199221, lo que se traduce en una reducción de la pendiente de la curva medio ambiental.
Al aplicar la prueba de Cusum y Cusum 22 se encontró que las curvas no sobre- pasan las bandas de confianza, por tanto, ambas pruebas confirman que no existe indicio de que el modelo presente quiebre estructural, sin embargo, gráficamente, para el caso del CO2 y el NOx sí se evidencia cierto quiebre. Se observa también que los modelos autorregresivos con orden 1 y 2 presenta retardos respectiva- mente, representados por los términos AR (1) y AR (2), son significativos al 1% y 5% para el monóxido de carbono, mientras que el término AR (1) es significativo al 1% para el óxido de nitrógeno, partículas contaminantes en el aire y para el óxido de azufre.
En cuanto al coeficiente de Gini, solo es estadísticamente significativo para el metano al 5%. Para todos los contaminantes con, excepción del óxido de azufre, el coeficiente de Gini guarda una relación negativa, es decir, un mayor nivel de des- igualdad reduce las emisiones contaminantes. Para este contaminante se encontró un quiebre estructural en el coeficiente de Gini en el 2011, posterior al quiebre, el coeficiente de Gini pasó a ser negativo.
Se realizaron las pruebas de raíz unitaria para cada serie y las pruebas de Dickey-Fuller y de Phillips Perron. En los seis contaminantes contemplados se rechazó la hipótesis nula de no estacionariedad (ver anexo). Al aplicar también las pruebas de esfericidad de los errores (insesgadez y eficiencia de Gauss-Markov), se concluyó que no existe autocorrelación, ya que el estadístico Durbin Watson no es próximo a 2, esto ocurre para el CO, CO2, metano, NOx, partículas y SOx. La razón por la cual determinados contaminantes se están reduciendo y otros no, puede deberse a procesos productivos más limpios en algunas actividades económicas que están incorporando medidas ambientales en su producción.
En la siguiente tabla se consolidan los resultados para el caso del PIB per cápita:
Tabla 3 Resultados consolidados para el PIB per cápita y su relación con los contaminantes en Perú
| Contaminante | Estadísticamente significativo (valor p-value) | Relación entre el PBI y el nivel de degradación ambiental | Fase de la CMK en la que se ubica el contaminante | Año de punto de quiebre (test de quiebre estructural Quandt- Andrews) |
|---|---|---|---|---|
| Dióxido de carbono (CO2) | SI | + | creciente | 2001 |
| Monóxido de carbono (CO) | SI | - | decreciente | -- |
| Óxido de nitrógeno (NOx) | SI | + | creciente | 2011 |
| Partículas contaminantes en el Aire | SI | - | decreciente | -- |
| Metano (CH4): | SI | - | decreciente | -- |
| Óxido de azufre (SOx) | SI | + | creciente | -- |
Fuente: elaboración propia
Gráficamente se puede ilustrar el tema de la siguiente manera:
ANÁLISIS SISTÉMICO DE LA CURVA MEDIO AMBIENTAL DE KUZNETS
3.1 Fundamentos de dinámica de sistemas
Según la System Dynamics Society, la dinámica del sistema es un enfoque asistido por computadora para el análisis y diseño de políticas. Se aplica a problemas dinámicos y se caracteriza por la interdependencia, retroalimentación de información y causalidad circular. Permite la creación de modelos que se pueden simular computacionalmente. El modelamiento empieza con la definición de los problemas de forma dinámica, la representación de las relaciones entre variables mediante mapas de influencia, para luego pasar a una fase de modelado, validación y simulación de políticas, como se verá más adelante.
Al respecto, García (2017, p. 28) precisa que “una cadena cerrada de relaciones causales recibe el nombre de bucle, retroalimentación o feedback”. Existen dos tipos de bucles: de reforzamiento (positivos) y de balanceo (negativos). Los de reforzamiento inducen a un crecimiento de la variable analizada (situación inestable), mientras que los de balanceo equilibran el sistema, lo conducen a una situación estable.
3.2. Uso de mapas de influencia de la dinámica de sistemas en la interpretación de las variables
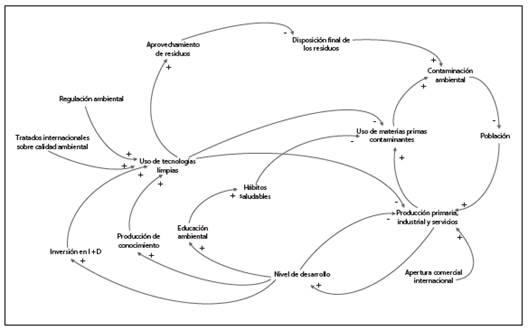
Para describir las complejas relaciones entre la economía ambiental y el resto de la economía y comprender las causas estructurales que provocan su comportamiento, se plantea un diagrama de influencias (figura 3) que permite explicar, no solo el comportamiento de las variables involucradas en la CMK, sino observar las diferentes interacciones entre las variables de todo el sistema y analizar su retroalimentación. Es importante anotar que es posible ampliar las fronteras de este diagrama empleando otras variables pertinentes.
En el modelo causal se identifican bucles de retroalimentación o reforzamiento cuyas interacciones entre sí producen el comportamiento dinámico de la degradación ambiental. Por ejemplo, el mayor tamaño de la población incide directa y proporcionalmente en el nivel de producción primaria, industrial y de servicios, lo cual conlleva mayor uso de materias primas contaminantes y deriva en un aumento de la contaminación. Este bucle de reforzamiento promueve el crecimiento del nivel de contaminación ambiental.
A la vez, existen varios bucles de regulación o de balanceo que limitan el crecimiento del nivel de contaminación. Por ejemplo, a mayor nivel de producción primaria, industrial y de servicios, se fomenta el desarrollo económico; a mayor desarrollo económico hay mayor inversión en investigación y desarrollo, lo cual promueve la inversión en tecnologías limpias, con la consiguiente disminución del uso de insumos contaminantes, y resulta en una reducción del efecto en la contaminación ambiental.
Asimismo, mayor nivel de desarrollo implica más producción de conocimiento, lo cual impacta con un incremento en el uso de tecnologías limpias y menor uso de materias primas contaminantes y por tanto, propicia menor contaminación ambiental. En el comportamiento dinámico de estos bucles se observan diferentes niveles de contaminación ambiental con respecto, por ejemplo, a la producción económica, que se refleja en el PIB (para el caso de hipótesis de Kuznets). El resultado final y evolutivo depende del nivel de fuerza de unos bucles sobre otros. En el presente caso, el segundo bucle descrito (de regulación) contrarresta los bucles de reforzamiento de la contaminación.
Desde la perspectiva de la dinámica de sistemas, los diferentes comportamientos anómalos de la curva de Kuznets, aplicados a países en vías de desarrollo, se pueden explicar a partir de los estados iniciales de los sistemas económicos de cada país. Lo anterior evidencia la adopción de diferentes rutas de desarrollo en cada uno y con ello, los efectos divergentes que estas rutas tienen en la contaminación ambiental. Esto es lo que la diferencia de la hipótesis de Kuznets la cual se basa en relaciones unidireccionales entre variables y no muestra la múltiple causalidad ni bucles de retroalimentación. La dificultad de la hipótesis de Kuznets para explicar estas anomalías en la degradación ambiental, hace necesario optar por un método más adecuado. La dinámica de sistemas resulta de gran ayuda para comprender y explicar mejor el comportamiento de la degradación ambiental.
Asimismo, cabe resaltar que el desarrollo de un modelo de dinámica de sistemas permitiría realizar simulaciones para crear escenarios en los cuales se podrían evaluar diferentes medidas de política económica. Estos escenarios nacen de los diferentes conjuntos de valores que puede tomar el sistema económico y que explicarían la hipótesis de Kuznets y sus anomalías. En ese sentido, la dinámica de sistemas es una herramienta muy útil para analizar los futuros viables, lo cual permite hacer estudios de prospectiva.
Mientras que la hipótesis de Kuznets pronostica un único escenario en el que la degradación ambiental comienza a disminuir una vez que se alcanza el turning point, la dinámica de sistemas puede generar escenarios que explicarían el comportamiento anómalo de esta degradación y permitiría formular políticas acordes con las particularidades de cada país.
3.3. Formulación del modelo de dinámica de sistemas para la cantidad de emisiones del CO2 en Perú
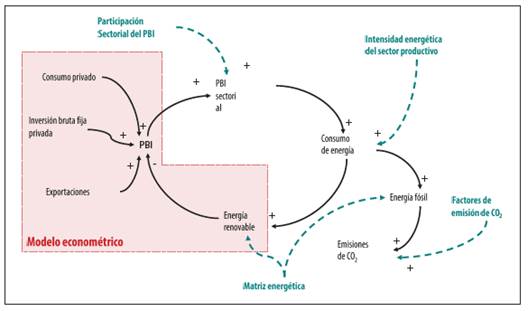
El objetivo era diseñar un modelo de dinámica de sistemas de los factores que afectan el contaminante CO2 y relacionarlos con las variables del sector real con el fin de simular escenarios del comportamiento del CO2. Como se mencionó, el modelo de referencia para elaborar el presente trabajo es el de Robalino, Mena y García (2014) para Ecuador. Primero se identificaron las variables que afectan el comportamiento de las emisiones de CO2 y la relación causal entre ellas (figura 4). Las variables para Perú son: PIB, participación sectorial del PIB, intensidad energética de cada sector productivo, consumo de energía −que a su vez se clasifica según su fuente en energía renovable y energía fósil−, matriz energética y las cantidades de emisiones de dióxido de carbono.
La cantidad de CO2 emitido en la atmósfera tiene varias conexiones con las variables del modelo, las líneas continuas representan la relación entre dichas variables y el mecanismo de retroalimentación; así, a mayor crecimiento económico, medido por el PIB, mayor PIB sectorial, las que a su vez demandan mayor consumo de energía. Este aumento en el consumo de energía origina mayor consumo de energía renovable y energía fósil, la cual induce a mayores emisiones de CO2. Por otro lado, la mayor energía renovable impacta de manera negativa en el PIB del país y con ello cierra el bucle del sistema.
Las líneas punteadas corresponden a términos de control que permiten la regulación de las emisiones del CO2 en el sistema, tales como los cambios en la estructura productiva sectorial del país, en la intensidad energética sectorial, en la matriz energética o en los factores de la emisión.
En cuanto a los tipos de variables, cualquier modelo dinámico contiene dos tipos de variables: de stock (existencias) y de flujo. Las variables de stock representan las acumulaciones dentro del sistema (como el PIB). Las variables de flujo representan los flujos en el sistema (como el incremento del PIB) que resultan del proceso de toma de decisiones. Otros parámetros dentro de la estructura de un modelo dinámico son las variables auxiliares (como la tasa de crecimiento del PIB) y por último, se tiene las constantes (PIB inicial).
De acuerdo con Robalino, Mena y García (2014), se calculan las emisiones de CO2 a partir de una variación de la identidad de Kaya. El modelo se divide en tres submodelos: submodelo econométrico del PIB, submodelo de la estructura sectorial productiva e intensidad energética, y submodelo de la intensidad energética de CO2.
Las emisiones de CO2 se puedes describir así:
donde C son las emisiones totales de CO2 (en un año dado); Cij son las emisiones de CO2 que se producen de un tipo de combustible j en el sector productivo i; Q es el PIB total de un país; Qi es el PIB generado por el sector productivo i; Ei es la energía consumida en el sector productivo i; Eij es el consumo total de energía del sector productivo i usando combustible de tipo j.
Para fines de este trabajo se adoptó la identidad de Kaya (Kaya y Yokorobori, 1997) y se utilizó Ej en vez de Eij, de este modo se agregó al modelo todo el consumo de energía por tipo de combustible.
La simulación de dinámica de sistemas del modelo para el caso peruano se realizó con el software Stella para Windows V10.1. El periodo de simulación establecido fue del 1994 al 2014 para calibrar el modelo, y luego del 2015 en adelante para crear escenarios.
A continuación, se describe cada submodelo del sistema.
3.3.1. Submodelo econométrico del PIB
Al igual que en el modelo de Robalino, Mena y García (2014), se usó una perspectiva económica ambiental para incluir la influencia del uso de energía renovable en la formación del PIB.
En teoría, la energía renovable puede impactar en el PIB a través de la expansión de nuevas empresas que consuman energía renovable o a través de la sustitución de la importación de energía fósil por renovable, que traerá consigo impactos, tanto directos como indirectos, sobre la balanza comercial y el PIB. Este submodelo que corresponde a la parte del crecimiento económico se construyó en base al modelo econométrico de la tasa de crecimiento interanual del PIB, cuyos coeficientes estimados se incluyeron en el modelo de dinámica de sistemas (figura 5).
Fuente: elaboración propia
Figura 5 Submodelo econométrico del PIB como input del modelo de dinámica de sistemas
Se buscaba modelar el PIB en función de variables macroeconómicas y energéticas. Robalino, Mena y García (2014) utilizan variables macroeconómicas como consumo privado, inversión privada y balanza comercial. Asimismo, también utilizan variables relacionadas a la actividad energética, como importación de energía y consumo de energía renovable. En este artículo se utilizaron las mismas variables con algunas modificaciones. Variables macroeconómicas: consumo privado, inversión bruta fija y exportaciones; para las variables energéticas solo se consideró el consumo de energía renovable, pues en Perú no se importa energía, como ocurre en Ecuador.
Se tomaron datos anuales correspondientes a las variables mencionadas, desde 1994 hasta el 2014, debido a restricciones de datos. Una primera restricción se refiere a la disponibilidad de datos sobre consumo de energía renovable en el país (solo existen datos desde 1990). En segundo lugar, solo existen datos de ponderadores o factores de emisión a partir de 1994. Por ende, solo se considera tal intervalo de tiempo y se recomiendan proyecciones no mayores a cinco años.
Las variables macroeconómicas están expresadas en valores reales en millones de soles del 2007, a excepción de las exportaciones que están en valor real en millones de dólares del 2007. La recopilación de estas variables proviene del Banco Central de Reserva del Perú. La variable consumo de energía renovable se expresa en toneladas equivalentes de petróleo (tep). Los datos de esta variable provienen de la Agencia Internacional de energía (AIE).
Previo al modelamiento econométrico, se realiza un análisis descriptivo de variables. Como las variables de nivel corresponden a una serie de tiempo, se debería trabajar con variables estacionarias para incluirlas en el modelo econométrico. Sin embargo, para el presente trabajo se ha considerado pertinente trabajar en tasas, eliminando la tendencia de las series. De esta forma se mejora la relación causal y el pronóstico del mismo, excluyendo la tendencia entre las series como un factor relevante para el análisis. Además, se evitan los problemas de escala y de diferencias en las unidades de las variables del modelo econométrico. Para ello se calculó la tasa de crecimiento de cada variable con el método aritmético de diferencias. Se empleó Stata14 como software econométrico.
El objetivo del modelo econométrico es observar las relaciones causales de forma directa entre las variables del modelo. Es importante el pronóstico de estas estimaciones porque formarán parte del modelo de dinámica de sistemas en el cual se busca simular determinadas situaciones referentes a la emisión de CO2. Se optó por un modelo MCO, el cual cumple con las especificaciones señaladas, además de ser una forma intuitiva de entender cómo será el mecanismo del modelo de dinámica sistemas, del cual forma parte el modelo econométrico.
Al inicio se habían considerado las mismas variables utilizadas por Robalino, Mena y García (2014). Sin embargo, debido a que luego se iban a estimar tasas de crecimiento de las variables para realizar la simulación, la variable balanza comercial, que empleó dicho estudio, arrojaba valores negativos crecientes, aún cuando se sabe que el resultado de la balanza comercial es fluctuante y no tiene una tendencia definida. En este caso, se realizó una descomposición de esta variable en importaciones y exportaciones, sin embargo, en un modelo previo las importaciones no fueron significativas, el modelo resultante se ilustra en la tabla 4.
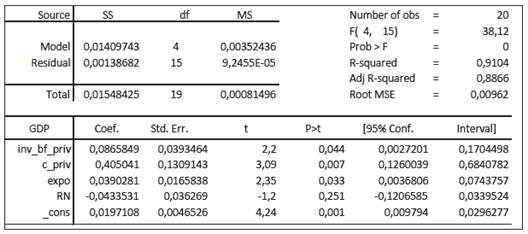
Tabla 4 Modelo econométrico para el PIB a ser incorporado en el modelo de dinámica de sistemas
Fuente: elaboración propia, en Stata con base a datos del Banco Central de Reserva del Perú y del Instituto Peruano de Economía.
Se observa que todas las variables del modelo son significativas a excepción de los recursos renovables (RN). Sin embargo, dado que es una variable de interés en el modelo y el objetivo es predecir el PIB, se considera dicha variable.
Referente al signo de los coeficientes, todos coinciden con la teoría económica, incluso los recursos renovables, pues mientras que en países desarrollados esta variable tiene signo positivo −debido a que el avance tecnológico permite aumentar la capacidad de sustitución de insumos más contaminantes por otros menos agresivos para el medio ambiente−, para el caso de países en desarrollo como Perú, el impacto dependerá de si en la economía los efectos de composición y tecnología contrarrestan el efecto escala. Es así que esta variable puede ser negativa para los países en desarrollo, pues es más difícil y costosa la implementación debido a la limitada capacidad tecnológica disponible o a que la importación de tecnología se da con cierto grado de obsolescencia o demora. Asimismo, se aprecia un alto R2, lo cual significa que los datos del modelo tienen buen ajuste al modelo propuesto.
A continuación, se presenta el modelo econométrico:
donde:
GDP: Tasa del producto bruto interno
inv _ bf _ priv: Tasa de la inversión bruta fija privada
c _ priv : Tasa del consumo privado
expo: Tasa de las exportaciones
RN: Tasa del consumo de recursos renovables
3.3.2. Submodelo de estructura sectorial productiva e intensidad energética
El consumo de energía se refiere al uso de energía primaria antes de la transformación en cualquier otra energía de uso final. Se da en toneladas equivalentes de petróleo (tep). El Banco Mundial define la intensidad energética como la relación entre el consumo de energía y el PIB.
En este trabajo se consideran tres sectores agregados para definir la estructura sectorial productiva: (1) industria, (2) transporte, y (3) otros (resto de sectores). Esta no es la división estándar de los sectores productivos, pero es más apropiada según la estructura del conjunto de datos y el objetivo de este trabajo. Los sectores se representan dentro del modelo por su contribución a la economía del país (Si), por su intensidad energética (EIi) y por su matriz energética (Mij). El índice i se extiende por cada sector de la estructura sectorial productiva y el índice j por cada tipo de fuente de energía: (1) petróleo, (2) carbón, (3) gas natural, y (4) renovable. La energía renovable está compuesta por la energía eléctrica, biocombustible, solar y eólica, pero para fines de esta investigación se compendiaron estas fuentes en una sola variable.
3.3.3. Submodelo de matriz energética e intensidad de CO 2
La intensidad de CO2 de un país corresponde a la relación de emisiones de CO2 y la energía total consumida expresada en términos de masa equivalente de petróleo. Mij es la matriz energética, pero es más conveniente sumar los diferentes sectores y agregar las contribuciones de combustibles fósiles. Por un lado, M1, M2 y M3 corresponden al consumo de energía de petróleo, carbón, y gas natural respectivamente. Por lo tanto, la proporción de energía fósil en el consumo total será M1 + M2 + M3. Por otro lado, M4 representa el consumo de energía de fuentes renovables. Por lo tanto, M1+M2+M3+M4=100%. Con el fin de simplificar la descripción, en este artículo se supone que M4 no contribuye a las emisiones de CO2.
Los factores de emisión, Uij, se toman del promedio de la relación de las emisiones de CO2 y el consumo de energía anual.
El modelo de bucles causales se muestra en la figura 6. El proceso de retroalimentación se puede describir partiendo del PIB, que se descompone según el sector productivo: mayor PIB implica mayor aportación al PIB por cada sector productivo. Esta producción sectorial tiene su equivalente en la energía consumida necesaria para producirla. El consumo de energía total se descompone en energía renovable y energía fósil. Esta última es la que contribuye a las emisiones de CO2. Por otro lado, la energía renovable producida y consumida ingresa como variable al modelo econométrico de la tasa de crecimiento del PIB.
3.3.4. Construcción del modelo de dinámica de sistemas
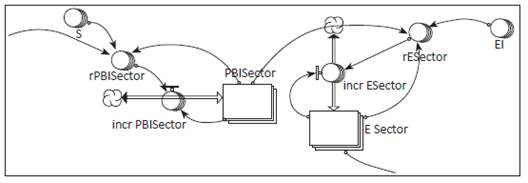
Este primer submodelo se construyó con base en el modelo econométrico de la tasa de crecimiento interanual del PIB (figura 7). En el software Stella se agruparon en vectores las tasas de crecimiento anual de la inversión privada, consumo privado y exportaciones (variable rVar). La energía renovable se separó porque viene del submodelo de intensidad de CO2 y matriz energética. Estas tasas se representan como niveles porque evolucionan con el tiempo, por ello se incluyen las tasas de segundo orden (r2Var) que permiten el crecimiento de las tasas variables del modelo econométrico. Para el ajuste de las tasas de primer orden se utilizan modelos geométricos de crecimiento.
En el segundo submodelo (figura 8) se utiliza la estructura productiva para desagregar el PIB neto, que entra como variable externa en los PIB sectoriales (industria, transporte y otros). Con el PIB sectorial del año anterior se construyen las tres tasas de crecimiento del PIB sectorial. Cada PIB sectorial se transforma en su equivalente a energía consumida por su actividad productiva. Para ello se utiliza la matriz de intensidad energética definida como el consumo neto de energía de un sector en su contribución a la formación del PIB neto.
Fuente: elaboración propia, en Stella
Figura 8 Submodelo de la estructura productiva e intensidad energética
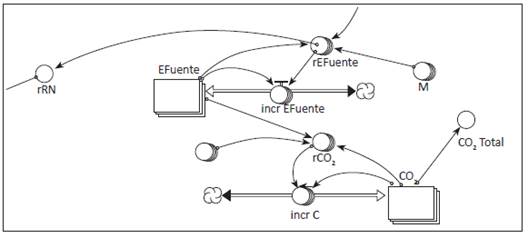
En el tercer modelo (figura 9) se utiliza la matriz energética y los factores de emisión para calcular las emisiones de CO2 anuales. El consumo de energía por sector productivo de los dos últimos periodos y la matriz energética se utilizan para construir las tasas anuales de crecimiento del consumo de energía por tipo de fuente y se desagrega el consumo de energía por sector para reagrupar según tipo de fuente (petróleo, carbón, gas natural, energía renovable).
Fuente: elaboración propia, en Stella
Figura 9 Submodelo de la matriz energética e intensidad de CO2
La estructura sectorial y la matriz energética actúan como desagregadores. La matriz de intensidad energética y la matriz de factores de emisión actúan como conversores.
El modelo completo de dinámica de sistemas integra los tres submodelos pre- sentados. Las variables utilizadas en el modelo de dinámica de sistemas se muestran en la tabla 5, las tasas de crecimiento para el modelo se presentan en la tabla 6.
Tabla 5 Relación de variables utilizadas en el modelo de dinámica de sistemas
| Variable | Descripción |
|---|---|
| CO2 | Vector de niveles de emisión de CO2 por tipo de fuente |
| CO2 _Total | Total de emisiones de CO2 |
| coef | Coeficientes del modelo econométrico |
| PBI_neto | PBI neto anual |
| PBISector | PBI sectorial anual |
| EFuente | Vector de niveles de consumo de energía por tipo de fuente |
| Esector | Vector de niveles del consumo de energía por sector productivo |
| incr_C | Vector de variación de emisiones de CO2 por tipo de fuente |
| incr_EFuente | Vector de variación de consumo de energía por tipo de fuente |
| incr_ESector | Vector de variación del consumo de energía por sector productivo |
| incr_rPBI_neto | Variación anual del PBI neto |
| incr_rPBISector | Vector de variación del PBI sectorial |
| incr_rVar | Variación anual de las tasas de los componentes econométricos |
| M | Matriz energética |
| EI | Matriz de intensidad energética |
| S | Matriz de estructura productiva |
| U | Vector de factores de emisión de CO2 |
| r2Var | Vector de tasas de segundo orden para los componentes econométricos (tasas de las tasas) |
| rCO2 | Vector de tasas de crecimiento de emisiones de CO2 por tipo de fuente |
| rEFuente | Vector de tasas de crecimiento de consumo de energía por tipo de fuente |
| rESector | Vector de tasas de crecimiento del consumo de energía por sector productivo |
| rPBI | Tasa de crecimiento del PBI |
| rPBISector | Vector de tasas de crecimiento del PBI sectorial |
| rRN | Tasa de crecimiento anual de energía renovable producida |
| rVar | Vector de variables de niveles de las variables econométricas (tasas) |
Fuente: elaboración propia
Tabla 6 Tasas de crecimiento utilizadas en el modelo de dinámica de sistemas (software Stella)

Fuente: elaboración propia
3.4 Simulación y creación de escenarios
Una vez diseñado el modelo de Forrester se procede a simular el sistema y los resultados se muestran en la siguiente figura:
Como se observa, se corroboran los resultados de Kuznets para el contaminante del CO2. Sin embargo, a partir de este modelo se pueden crear escenarios mediante nuevas simulaciones con cambios en el sistema mediante cuadros de mando que permiten modificar tasas, factores o incluir variables. Por ejemplo, se pueden modificar los valores de las variables que originan el modelo, como el consumo energético por sectores y por contaminantes, y todas las variables que conforman el PIB, con el fin de analizar sus efectos en la economía y en la contaminación ambiental.
4. CONCLUSIONES
Los resultados econométricos evidencian que solo tres de los seis contaminantes se encuentran en la primera etapa de la curva medio ambiental, dióxido de carbono, óxido de nitrógeno y óxido de azufre, mientras que existen contaminantes para los cuales un mayor nivel de ingreso deviene en una reducción de sus emanaciones, tales como el monóxido de carbono, el metano y las partículas en el aire.
A través del mapa de influencias, la dinámica de sistemas permite identificar relaciones causales que explican la compleja realidad del sistema de degradación ambiental, lo que permitió superar el carácter lineal y unidireccional del modelo clásico de Kuznets, al visualizar los bucles de reforzamiento y de balanceo del sistema. De esta manera se observó que la cantidad de CO2 emitido a la atmósfera tiene varias conexiones con las variables del modelo. El mecanismo de retroalimentación se describe de la siguiente manera: a mayor crecimiento económico −medido por el PIB− mayor PIB sectorial, que demanda mayor consumo de energía. Este aumento en el consumo de energía origina mayor consumo de energía renovable y energía fósil, la cual induce a mayores emisiones de CO2. Por otro lado, la mayor energía renovable impacta a su vez en el PIB del país y con ello cierra el bucle del sistema.
Asimismo, se visualiza que los términos de control que permiten la regulación de las emisiones del CO2 en el sistema están dados por los cambios en la estructura productiva sectorial del país, cambios en la intensidad energética sectorial, en la matriz energética o en los factores de la emisión. De esta manera se muestra que con el uso de cuadros dinámicos de mando se relacionaron variables del sector real con la degradación ambiental, medidos por el contaminante CO2, lo que permite generar escenarios para la formulación de políticas y planes de acción en las variables generadoras del modelo.