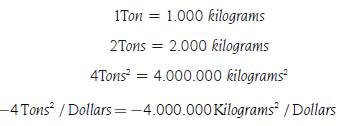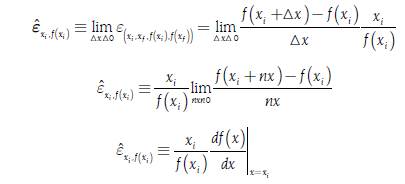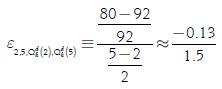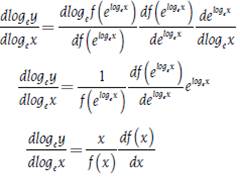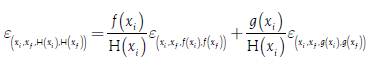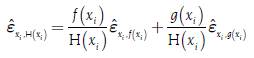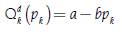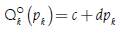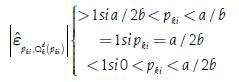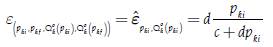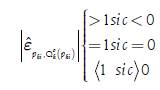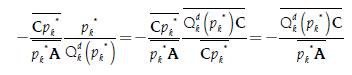INTRODUCTION
The concept of elasticity1 is central in economics to explain the behavior of economic agents where it is included as a subject within the contents of introductory courses in undergraduate economics for future economists, business managers, public accountants, and engineers. However, when it is taught in undergraduate programs it is presented as a merely definition and not with a clear motivation about why it is necessary to introduce it. Apart from economics textbooks like Becker (2007) and Allen (1938), the majority of introductory material deal with the concept as a simple definition, without telling a clear reason of why it is required to use it. The goal of this paper is to explain in a clear way why it is necessary to introduce the concept where it is suggested an approach of tea ching and presenting to students with different levels of mathematical sophistication. To fulfill this objective, the concept’s main properties that have been identified in the literature are indicated from a historical perspective, to illustrate a way of teaching the notion of elasticity in a discrete or continuous terms and using geometric arguments or algebraic expressions depending on the profile of the student. In this way, students can better understand the concept since their previous knowledge is taken into account when the idea of elasticity is taught for the first time.
The article is organized in five sections: Section 1 establishes the precise definition of elasticity in economics, why is it used, and indicates another alternative definition of elasticity for the discrete case. In section 2, a short introductory history of the development of elasticity properties in economics is presented. Section 3 shows the price elasticity of demand and supply for linear and differentiable functions, presents a geometric interpretation of the price elasticity of demand and supply for non-linear and differentiable functions and the price elasticity of the demand for different functional forms commonly used in the literature is calculated. Section 4 identifies different strategies that can be used to teach the concept, and section 5 presents the main conclusions.
1. THE CONCEPT OF ELASTICITY IN ECONOMICS
1.1 The definition of elasticity in economics and why it is used
In economics, it is of great interest to know what happens to a variable when another one changes, where the former depends on the latter and it is assumed that everything else remains constant. For example, in consumer theory, it is assumed that the individual demand for a product depends directly on its price, on other products that are complementary or substitutes, and on the income of the individual. Under the previous case, economists are interested in knowing the direction and magnitude of a certain increase in the price of the product over the individual demand, assuming that all the remaining variables mentioned above do not change.
The tool that can be used initially to perform this analysis is the concept of slope. If  is the quantity demanded by a consumer of a product, k, pk is its price, pj is a vector of complementary or substitute products, and m is the income of the individual, the idea would be to estimate the slope of the individual demand function with respect to the price of the good, either for the discrete or continuous case:
is the quantity demanded by a consumer of a product, k, pk is its price, pj is a vector of complementary or substitute products, and m is the income of the individual, the idea would be to estimate the slope of the individual demand function with respect to the price of the good, either for the discrete or continuous case:
Where ∆pk>0 is the magnitude in which pk increase and where for the continuous case it is assumed that ∆pk→0.
However, there is a problem with the slope of the individual demand function since it varies with the units in which the quantity demanded of the product and its price are measured. To understand this problem, it is necessary to understand the units in which the slope is expressed, which depends on the individual quantity demanded and the price of the product. In general, the units in which a price is expressed are monetary units, which we will call M, over the units in which de product is measured, which we will call K: In other words M/K. For example, a salary that is paid monthly in dollars would be expressed in Dollar / 1Month, or the price of a good that is measured in kilograms and paid in dollars would be expressed in Dollars/Kilograms. In that sense because the slope of the individual demand function is a ratio between the subtraction of some quantities demanded in the numerator and a subtraction of prices in the denominator it would be expressed in K / (M/K) = K2/M. Due to the above, if the way of measuring the product or the monetary units is changed, the slope will change.
As an example, suppose that the individual demanded quantity of a product is measured in tons and paid in dollars. In this sense, the slope of the individual demand function with respect to the price of the product would be expressed in Tons/(Dollars/Tons) = Tons2 / Dollars. Also, assume for simplicity that the product does not have other complementary or substitute products, and that the individual demand does not depend on the income of the individual, where it is given by:
Therefore, we would have that the slope and their respective units would be given by −4 Tons 2 / Dollar. If the product is measured in Kilograms, the equivalent slope, as mentioned in Becker (2007, p. 12), would be:
In other words, when changing the units in which the product is measured, going from Tons to Kilograms, we would have that an increase in the price would decrease the quantity no longer simply in four but in four million. Due to the previous problem, in economics the concept of elasticity is introduced where the changes of one variable over another, keeping everything else constant, are not examined in absolute but in percentage terms to eliminate the units in which a proportion is expressed. In general, the concept of elasticity is defined as the relationship between the relative change of a dependent variable over the relative change of an independent variable. In economics, simple percentage changes are used for measuring the relative change in principle, so if the independent variable is denoted as x and the dependent variable as (f(x) the elasticity εx i , f (x i ) in the points (x i , s f , f(x i ), f(x f )), is defined as follows:
Where x f is the final value of the independent variable, x i is the initial value of the independent variable, f(x f ) is the associated value of the dependent variable with xf, f(x i ) is the associated value of the dependent variable with x i and where it is assumed that f(x i ) ≠0, x i ≠ 0, x f ≠x i so the value of εx i , f (x i ) is defined.
In that sense, f(x f ) - f(x i )/f(x i ) represents the percentage change of the dependent variable when passing from value f(x i ) to value f(x f ), using as a point of reference the value f(x i ); and in a similar way, x f - x i /x i represents the percentage change of the independent variable when passing form value x i to value xf using the value xi as a point of reference. In that way, both in the numerator and in the denominator of the expression [4] the units in which f(x) or x is measured are irrelevant since they are canceled, and εx i , f (x i ) will not have any associated units. In addition, the expression [4] can be reorganized in the following way:
In that way, f(x f ) - f(x i )/x f - x i represents the slope of the function f using the values x f and x i to calculate it. If we define x f - x i =∆x, we can use the tools of differential calculus to define the elasticity using the concept of derivate with x f = x i + ∆x and ∆x∆0 xthrough the expression [5], as it is mentioned in Allen (1938, p. 251):
If we apply the concept defined in [4] and [6] to the individual demand of a consumer to examine how a change in price affects the quantity demanded, these expressions are known as price elasticities of demand. To interpret the values of this type of elasticity from the economic point of view, we must define for the discrete case of what initial price p i we are starting and at what final price pf we are arriving; and for the continuous case, which is the price p i in which we are calculating it. As an example, let us take the case in [2] assuming we increase the price from 2 dollars/ton to 5 dollars/ton, where the values of the elasticity would be given by the following:
In that sense, the value of -0.13/1.5 for the discrete case will mean that an increase in 150 % in the price, starting from 2 dollars/ton and arriving to 5 dollars/ ton, generates an approximate decrease of 13 % in the quantity demanded of the product assuming that everything else remains constant. On the other hand, for the discrete case, it would mean that a 100 % increase in the price, starting from 2 dollars/ton, generates an approximate decrease of 9 % in the quantity demanded of the product, assuming that everything else remains constant.
1.2 Another alternative way to measure the elasticity in the discrete case and why is it used
in the calculation of elasticity through expression [4], it is important to keep in mind that this definition uses simple percentage changes. By definition these ones are not symmetric, as it is mentioned in Tornqvist, Vartia, & Vartia (1985), in the sense that it is not the same to move from point x i to point x f than from point x f to point x i in absolute value. As an example, and using the individual demand [2], if we start from a price of 2 dollars/ton to 5 dollars/ton we would have, based on the expression [7], that a 150 % increase leads to a 13 % decrease in the quantity demanded. It would be desirable that if we examine no longer an increase but a decrease in the price from 5 dollars/ton to 2 dollars/ton, we would have a decrease of 150 % in the price that leads to an increase of 13 % of the quantity demanded. In other words, the latter is an effect of the same magnitude as when we decreased the price from 2 dollars/ton to 5 dollars/ton. However, this does not happen since the reference points x i and f(x i ) change when using the expression [4]. In our example, the elasticity would be given by:
In any case, it is important to point out that in the continuous case of the calculation of the elasticity, the previous problem is irrelevant given that this variable is being calculated at a certain point, and therefore its value can naturally change. In that sense, if we calculate the elasticity using the individual demand [2] for the price 5 dollars/ton based on the expression 6, we would have the following:
To solve the above-described problem regarding the calculation of elasticity, in the discrete case, in economy the concept of arc elasticity was introduced. There are different ways to define this variable in the literature 2, but a usual formula to do it was proposed by Allen and Lerner (1934). According to them, the arc elasticity, arc ε (x i ,x f ,f (x i ),f (x f )), in the points x i , x f , f(x i ), f(x f ), is defined as:
In that way, when you use the arc elasticity based on the proposal of Allen and Lerner (1934) this variable is equal in absolute value when you start from the point xi to the point xf and when you start from the point xf to the point xi because in both cases the reference points are (x f + x i )/2 and (f(x f ) + f(x i ))/2. For our example, based on the expression [2], if we start from a price of 2 dollars/ton to a one of 5 dollars/ ton or from a 5 dollars/ton price to a 2 dollars/ton one, the arc elasticity would be given by the following:
2. A SHORT INTRODUCTORY HISTORY OF THE DEVELOPMENT OF ELASTICITY PROPERTIES IN ECONOMICS
The concept of elasticity was introduced in an informal way by Marshall (1890, pp. 162-174) in his book “Principles of Economics” —specifically in Book III, Chapter III—, but also in a more formal manner in an appendix of mathematical notes within the same book in pages 738-740. Although, as mentioned by Newman (2008), there were precursory ideas developed by Antoine Augustin Cournot that approached the concept, which can be found in Cournot (1897)3. There, for example, in page 56 of Chapter V, using the notation developed above, the maximum income that a monopoly can obtain if it knows the market demand is examined, and that is given by:
If we try to find the price, p k *, that maximizes the income of the monopolist. A necessary condition for both discrete and continuous cases is this:
Although Antoine Augustin Cournot did not further develop these expressions, both [14] and [15] can be expressed in terms of the price elasticity of demand:
Where π =  in [16].
in [16].
The expression [13] can also be understood as the expenditure that a consumer has, and where it can be analyzed if it increases, decreases or remains constant in the face of an increase in the price. In the discrete case, if the elasticity of the demand is greater, less or equal to 1/π, then the expenditure increases, decreases or remains constant. Similarly, for the continuous case, if the elasticity of demand is greater, less or equal to —1, then the expenditure increases, decreases, or remains constant. Based on the previous result, it is possible to establish relationships between quantities demanded and prices, where if for a combination of prices (p
k1
,p
k2
)and quantities  , it is true that
, it is true that  . In other words, the expenditure is the same and does not change, the price elasticity of demand must be equal to−1/ Π, and where if 6pk → 0, this elasticity will tend to -1. The historical importance of this result lies in that it was used by Allen and Lerner (1934) to establish a property that should fulfill the definition of arc elasticity, and that links Antoine Augustin Cournot’s early ideas with Alfred Marshall’s definition regarding the price elasticity of demand.
. In other words, the expenditure is the same and does not change, the price elasticity of demand must be equal to−1/ Π, and where if 6pk → 0, this elasticity will tend to -1. The historical importance of this result lies in that it was used by Allen and Lerner (1934) to establish a property that should fulfill the definition of arc elasticity, and that links Antoine Augustin Cournot’s early ideas with Alfred Marshall’s definition regarding the price elasticity of demand.
Additionally, the reference point regarding whether the elasticity of demand is greater, less or equal to -1 allowed more general categories to be established with respect to any type of elasticity. In the economic literature, an elasticity is elastic if it is greater than 1 in absolute value; unitary if it is equal to 1 in absolute value; and inelastic if it is less than 1 in absolute value. In this way, it can also be compared if the percentage increase or decrease of one variable over another variable, that depends on it, increases or decreases more, equal or less in percentage terms.
In the development of the concept of elasticity, another type of property that met this variable was also found, exploiting the fact that in economics usually we work with positive magnitudes. If you have a function y = f(x) such that y > 0 and x > 0, it can be expressed as logey = logef(elogex) where loge is the natural logarithm. In that way, we can obtain the following result, as mentioned by Allen (1938, p. 251):
Where the elasticity can be expressed in terms of logarithmic derivatives, as mentioned by Newman (2008). There is also a calculus of the elasticities where it is possible to derive expressions for the elasticity of the addition and multiplication of functions, and therefore of the subtraction and division of functions for both the continuous case, as mentioned by Allen (1938, pp. 252-253), and the discrete case. In the case of addition of two (2) functions, elasticity would be given by expressions [19] and [20] for the discrete and continuous cases:
Where H(x i ) = f(x i ) + g(x i ), H(x f ) = f(x f ) + g(x f ) and each of the elasticities, ε (x i ,x f ,H(x i ),H(x f )) y ε ˆ x i ,H(x i ), are expressing a weighted average of the elasticities of f(x) and g(x). In the case of the subtraction of two (2) functions, it can simply be defined as g(x) = -j(x) to obtain a formula in both the discrete and continuous cases. In the case of the multiplication of two (2) functions, elasticity would be given by the expressions [21] and [22] for the discrete and continuous cases:
Where G(x i ) = f(x i )g(x i ), G(x f ) = f(x f )g(x f ), and ε(x i ,x f ,H(x i ),H(x f )) is the addition of the elasticity of f(x) and g(x), but where the elasticity of the latter is multiplied by f(x f )/f(x i ). In the case of ε ˆx i ,G(x i ), it is simply the addition of the elasticities of f(x) and g(x). For the case of the division of two (2) functions, it can simply be defined as g(x) = 1/j(x) to obtain a formula in both discrete and continuous cases.
Finally, based on what was pointed out by Nievergelt (1983), it is possible to recover the function from its elasticity while a differential equation can be solved.
For any x, the elasticity is given by the expression [6] without evaluating it in xi, in other words:
Where P(x) is the functional form that the elasticity takes, that can depend on x. For example, if P(x) is equal to a constant l, the expression [23] becomes in a separable differential equation whose only solution, as mentioned by Nievergelt (1983, p. 264), is given by the following:
3. ELASTICITY CALCULATION AND GEOMETRIC INTERPRETATION OF SOME DEMAND AND SUPPLY FUNCTIONS
3.1 Price demand and supply elasticity of lineal and differential functions
The use of demand and supply lineal functions that also depends only on the price of the product being modeling, more than representing a realistic case, has the advantage to show the student a clear way to identify the difference between the slope and the elasticity of the function in a graphic and algebraic way. Both demand  and supply Q
0
k
lineal functions for a product k with the characteristics mentioned above are given by:
and supply Q
0
k
lineal functions for a product k with the characteristics mentioned above are given by:
Where a > 0, b > 0 y d > 0. In this way, the price elasticity of demand both for the discrete and the continuous case is given by:
Where it is possible to show that:
Figure 1 graphically shows the above.
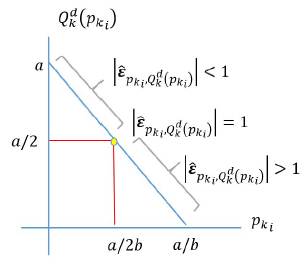
Source: Prepared by the author.
Figure 1 Price demand elasticity of a lineal and differential function
The previous result of the demand function allows the student to understand that elasticity can vary in a function where the slope, given by -b, is constant. The price elasticity of supply for both discrete and continuous cases is given by the following:
Where it is possible to show, as mention in Mishan (1958), that:
Or, in a graphical way:
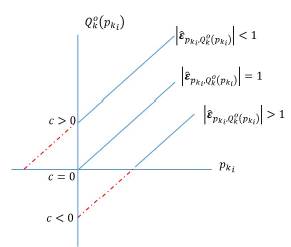
Source: Prepared by the author.
Figure 2 Price supply elasticity of a lineal and differential function
The previous result of the supply function allows the student to understand that elasticity can vary even if the slope of the function is the same, i. e., d.
3.2 Geometric interpretation of price point elasticity of demand and supply of non-lineal and differential functions
Based on the previous results of demand and supply functions that are linear and differentiable, it is possible to point out a geometrical interpretation of elasticity that is calculated at a certain point, as it was pointed out by Marshall (1890). For the case of the demand, let us assume a function Q d k (p k ) as noted below.
Using the definition of price elasticity of demand and the previous graphic, it is possible to establish relations between the segments to express the concept of price elasticity of demand in another way, based on what Marshall (1890, p. 738, Note IV) pointed out:
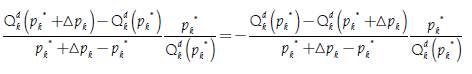
Where by similarity between the triangles ΔCDE y ΔCpk *A, 0 it is true that:
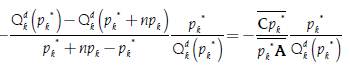
We also have that 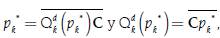 , where we have that:
, where we have that:
On the other hand, by similarity between the triangles ∆BQdk (pk*)C and ΔCpk*A it is true that  , that is
, that is  . In that sense, we have that:
. In that sense, we have that:
The previous result means that if we calculate the price elasticity of demand at the point
C,
it is equal to the relation that exists between the segments 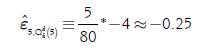 and
and  that make up the slope of the function in that point. Also, if the function takes the form indicated in [24], then, for any point throughout the function, the ratio of the segments that make up the slope is constant and equal to the absolute value of l.
that make up the slope of the function in that point. Also, if the function takes the form indicated in [24], then, for any point throughout the function, the ratio of the segments that make up the slope is constant and equal to the absolute value of l.
For the case of the supply, let us assume a function Qo K (Pk)as noted below, where three (3) possible cases should be considered.
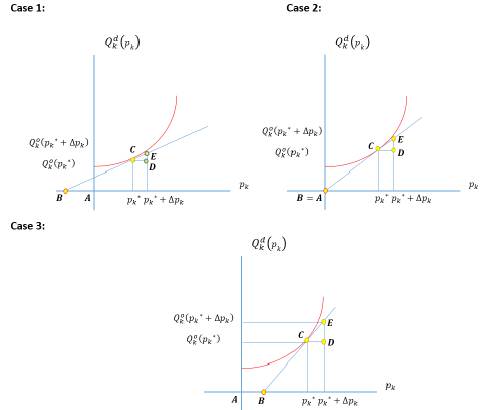
Source: Prepared by the author.
Figure 4 Non-lineal and differential supply function with different slopes
Using the definition of price elasticity of supply and the previous graphics, it is possible to establish relations between the segments to express the concept of price elasticity of supply in another way, as Mishan (1958, p. 64) established:
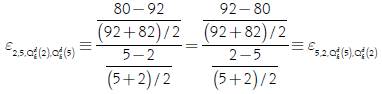
Where by similarity between the triangles ∆CDE y ∆Cp*B, it is true that:  Also, we have that
Also, we have that 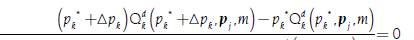 and
and  where we would have that:
where we would have that:
In Case 1 , in Case 2
, in Case 2  and in Case 3
and in Case 3 The previous result means that if we calculate the price elasticity of supply at the point
C, it is equal to the relationship that exists between segments
The previous result means that if we calculate the price elasticity of supply at the point
C, it is equal to the relationship that exists between segments  and
and  .
.
3.3 Functional forms of price-dependent demand functions without price competition and its point price elasticities of demand
One of the most important aspects for a company lies in knowing the demand of the product that it offers in such a way that the uncertainties in the different activities that it carries out, as well as the decisions made within the organization, can be reduced. Due to the above, different functional forms of demand functions have been proposed in the literature which depend on the operational and marketing activities that the company carries out to model consumer behavior. According to Huang, Leng, and Parlar (2013), the most common demand models depend on variables such as prices, rebates, lead time, space allocation, quality and advertising when all of them apply to a single company, or if there is a strategic interaction between rival companies.
This section shows the functional forms of the most common demand functions used in the literature depending solely on price, applied only to a company and with the calculation of point price elasticity of demand as a reference to illustrate concrete examples of the concept (table 1).
Table 1 Price-dependent demand functions applied for a single company and its point price elasticities of demand

Source: prepared by the author, based on Huang, Leng, and Parlar (2013, p. 561).
The use of particular functional forms of point price elasticity of demand allows to explore and generate discussions about desirable properties that this variable could have according to consumer behavior. As an example, linear, exponential, and logarithmic models have point price elasticities of demand that increase in absolute value as the price increases. On the other hand, the price point elasticity of the demand does not change with the price in the isoelastic model, but remains constant. In the case of logit model, if it is true that loge ½ <-bpk, then the point price elasticity of demand decreases in absolute value as the price increases.
4. STRATEGIES THAT CAN BE USED TO TEACH THE CONCEPT OF ELASTICITY
The way in which a topic is taught in undergraduate programs depends, to a large extent, on the tools which the students already have. In the case of the concept of elasticity, its teaching is quite flexible since it can be treated in discrete or continuous terms, as well as in algebraic or geometric ways. To teach the concept, the first strategy is to introduce the idea of slope by pointing out its limitations with respect to the problem of units and why elasticity is introduced as a way of solving it, as discussed in the opening parts of subsection 1.1.
If the students do not have the necessary knowledge of differential calculus, both the slope and elasticity can be introduced in discrete terms using linear functions, such as those indicated in subsection 3.1, indicating the difference between the slope and the elasticity of a function. Additionally, section 2 can be covered, with respect to the historical review, addressing only the topics that were treated in a discrete way. Also, the concept can be explained geometrically using the concept of similarity of triangles, as in subsection 3.2.
If the students have knowledge in differential calculus, subsection 1.2 can be covered by showing the difference between continuous and discrete cases of elasticity. The historical review of section 2 may also be covered without including the last part if the students have not taken a course in differential equations. It would also be recommended to cover subsection 3.1 as it shows the students the difference between the slope and elasticity of a function in a clear way. Subsection 3.2 would be optional if the goal is to explain the subject in geometric terms. Finally, concrete functional forms of elasticity could be revised using demand functions usually used in the literature and developed in subsection 3.3. In the case of students that have the knowledge of differential calculus and differential equations, all sections could be covered, but subsection 3.2 is left as an option and emphasis should be placed on how the function could be recovered through the possible solution of a differential equation.
5. CONCLUSIONS
Throughout this paper, different aspects of the concept of elasticity were presented with the purpose of pointing out different ways of teaching the concept, according to the level of knowledge that students have when they take an introductory course in economics. Regardless of the mathematical sophistication that students have, the concept can be presented as a solution to the problem of units in continuous or discrete terms when using the slope of a function. Additionally, it was pointed out how the subject can be introduced in algebraic terms or using basic geometry reasoning where it can be applied for both simple and non-linear functions. In this way, the teaching of the concept becomes flexible enough to introduce it to a wide audience of students so that the lack of knowledge of the tools of differential and integral calculus will not be an impediment to understand the general idea of the notion of elasticity. However, if students have these tools, it is possible to develop additional properties of the concept and examine different applications using functional forms of demand functions that are typically used in the related literature. In this way, considering the previous knowledge of the student and identifying the limitations that the introductory texts of economics have when presenting the concept, the notion of elasticity can be taught in a more adequate form.