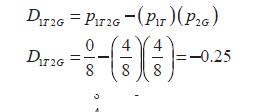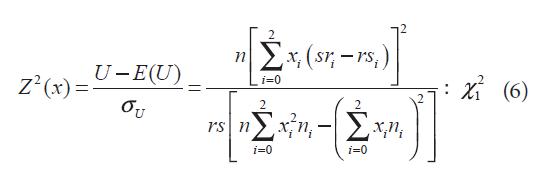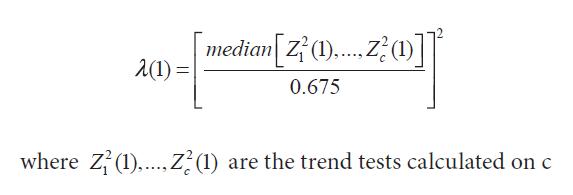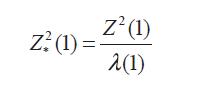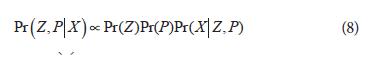Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Agronomía Colombiana
versão impressa ISSN 0120-9965
Agron. colomb. v.29 n.3 Bogotá set./dez. 2011
PLANT BREEDING, GENETIC RESOURCES & MOLECULAR BIOLOGY
Association mapping, a method to detect quantitative trait loci: statistical bases
Mapeo por asociación, un método para la detección de loci de rasgos cuantitativos: bases estadísticas
Gustavo Gómez1,María Fernanda Álvarez2 and Teresa Mosquera.2,3
1Agreliant Genetics. Westfield, IN (United States).2Department of Agronomy, Universidad Nacional de Colombia. Bogota (Colombia).
3Corresponding author. tmosquerav@unal.edu.co Received for publication: 13 December, 2010. Accepted for publication: 2 November, 2011.
ABSTRACT
Traditionally, QTL mapping has been used as methodology to understand the genetic control of polygenic traits and has been useful for identifying QTL in different species, however QTL mapping presents limitations, such as the difficulty to build segregating populations in some species, the presence of only one meiotic generation and the reduced genetically diversity derived of just two parental. Recently, association genetics studies are becoming an important methodology to identify quantitative trait loci and to find diagnostic molecular markers associated with complex traits. This methodology overcomes some barriers of QTL mapping and it is an alternative to apply in plant breeding in direct way. However, it is necessary to considerer important aspects in this methodology to avoid false associations between trait-markers. Association genetics employs as parameter linkage disequilibrium to find these associations. Here we present methods to analyze and establish population structure, factors that affect linkage disequilibrium and how to measure it and methods to perform association mapping
Key words: association genetics, linkage disequilibrium, population structure, genetic mapping, complex traits.
RESUMEN
Tradicionalmente, el Mapeo de QTL ha sido usado como metodología para aproximarse a la comprensión del control genético de rasgos poligénicos y ha sido útil en la identificación de QTL en diferentes especies, sin embargo presenta limitaciones como la dificultad de construir poblaciones segregantes en algunas especies, contar son solamente una generación meiótica. y visualizar únicamente la diversidad genética derivada de dos parentales. Recientemente, los estudios de Asociación Genética se han posicionado como una metodología importante para la identificación y localización de loci de rasgos cuantitativos y para encontrar marcadores moleculares diagnóstico asociados con rasgos complejos. Esta metodología resuelve algunas barreras del Mapeo de QTL y es una alternativa para aplicar en mejoramiento de plantas de manera directa. Sin embargo es necesario considerar aspectos importantes para evitar falsas asociaciones entre rasgo y marcador. En este artículo presentamos métodos para analizar y establecer la estructura poblacional, factores que afectan el desequilibrio en el ligamiento y cómo medirlo y métodos para realizar el mapeo por asociación.
Palabras clave: estudios de asociación genética, desequilibrio en el ligamiento, estructura de población, mapeo genético, caracteres complejos.
Introduction
Breeding solutions for the next 40 years should be supported on diversity, this holds up for food security on the world wide. The common crops have a narrow genetic pool due to domestication. In contrast, theirs wild relatives as a result of genetic history and selection pressure are becoming in reservoirs of natural genetic variation. Genes associated with desired agronomic traits such as higher yield or disease resistance that could be lost in the plant breeding process of a crop can be restored using these wild species. The problem for breeder is to find the genes and find an efficient way to trace the genes and to incorporate them in breeding populations (Abdurakhmonov and Abdukarimov, 2008).
When breeders work with a particular trait in a plant species, they start to work with the genetics of the trait. Many agricultural characteristics are controlled by polygenes and are greatly dependent of genetic x environment interactions (Abdurakhmonov and Abdukarimov, 2008). In an aim to work with the patterns of segregation and inheritance for breeding those traits, we think about the positions of the traits in a genetic map. Currently, when the position of a gene controlling traits is inferred we work with tools of genetic or physical mapping, depending on the information available for the species and the trait.
Traditionally it has been a challenge for breeders to work with quantitative trait loci (QTL), with the development of molecular markers technology, it has been possible to follow QTL segregation detecting markers linked to traits of interest and assessing effects, number and location of QTL in chromosomes. An alternative to QTL mapping is association mapping also called association genetics, association studies and linkage disequilibrium mapping (Chakraborty and Weiss, 1988; Kruglyak, 1999). These two methodologies have been advocated as the method of choice for identifying loci involved in the inheritance of complex traits (Risch and Merikangas, 1996).
Association mapping seeks to identify specific functional variants (loci, alleles) linked to phenotypic differences in a trait to facilitate detection of trait causing DNA sequence polymorphisms and selection of genotypes that closely resemble the phenotype (Oraguzie et al., 2007). In order to identify these functional variants it requires high throughput markers like single nucleotide polymorphisms (SNPs).
Molecular markers are used not just to generate genetic maps but also to locate the places of interest in those maps with its incidence in the expression of the trait. That is because they are used in marker assisted selection programs. To improve the breeding methods efficiency, breeders are using markers assisted selection techniques that show great advantages compared with traditional selection methods based on phenotypic traits evaluation. Molecular techniques allow accurate selection in early stages focusing directly in its genetic base (Gupta et al., 2005; Mackay and Powell, 2007; Simko et al., 2006; Sattarzadeh et al., 2006).
In order to locate QTL in a genetic map relatively few techniques have been developed, one of those is linkage mapping. Linkage mapping is the traditional method for QTL mapping, it implies to generate simple crosses derived populations and to estimate marker-gene recombination frequencies. Population mapping is frequently developed from diploid parental that are originated partially or completely from wild species. Such populations show only a small proportion of all the possible alleles. In contrast, another method is association mapping based on linkage disequilibrium (LD) concept, it is a method that exploits the diversity observed in existent cultivars and in breeding lines, without developing new populations (Gebhardt et al., 2004; Simko et al., 2004a; Simko et al., 2004b; Gupta et al., 2005; Mackay and Powell, 2007).
Most of the important limitations for linkage mapping can be overcome using association genetics. Association genetics does not require building segregating populations and it can employ larger germplasm exploiting the natural variation that exists in the available germplasm and resolution for association could be of at least of 5 cM depending on LD decay of the species.
Principles of genetic mapping population
Genetic mapping is mainly employed with two aims: to identify genetic factors or loci that influence phenotypic traits and to determine recombination distance among loci (Meksem and Kahl, 2005). As a condition for mapping the traits to be studied must be polymorphic. One way for detecting those polymorphisms is using molecular markers.
Genetic mapping by linkage is supported in genetic recombination, as condition for mapping a particular trait. This trait should be polymorphic, displaying preferably a wide variation among the individuals under study. When applying molecular markers in staid of a phenotypic trait these markers should be polymorphic as well, showing allelic variation. The selection of polymorphic markers required for QTL and single trait mapping depends on the existing knowledge regarding the species to study. In species without detailed information of its sequence the candidate gene approach may be used. This approach is based on the production of markers from gene sequences that they have been observed to take place or they are suspected that have a functional role in the selected trait (Gebhardt, 2004; Salvi and Tuberosa, 2005; Gebhardt et al., 2007).
QTL mapping begins with the gathering of genotypic and phenotypic data from a segregating population, and it is followed for a statistical analysis where all the major loci responsible of the trait variation are located. This analysis usually referred as primary QTL mapping could locate a QTL in an interval of approximately 10 to 30 cM, which may include several hundred of genes. Therefore, the genetic resolution has to be improved by assigning a QTL to the shortest chromosome segment including ideally one single gene. The final goal is the identification of DNA coding or not coding sequences responsible for QTL (QTL cloning). Two methods have been employed for verifying the association between the shortest possible region of a chromosome tagged using molecular markers and the value of the studied trait: positional cloning and association mapping (Salvi and Tuberosa, 2007). QTL cloning is difficult because of the resolution limitations, even though many QTL had been cloned since 2001 when the first QTL was cloned in Arabidopsis (El-Assal et al., 2001) but also in that year one QTL from rice was cloned as well, since this at least 20 QTL were cloned (Salvi and Tuberosa, 2005).
Positional cloning allows QTL resolution but it is necessary to produce a second and larger mapping population of 2000 or more F2 plants derived from a cross between two parental nearly isogenic lines with alleles functionally different in the targeted QTL. These parental lines are called QTL-NILs (quantitative trait loci-nearly isogenic lines). The generation of these lines can be archived doing marker assisted backcrosses or iteratively identifying and selfing individuals that are heterozygous at the QTL region. The production of such NILs can last several years depending on the plant material. Other important aspects to consider are the genetic limited variability as a result of the use of only two parental. The generated population could segregate for just a fraction of many QTL that may affect the same trait in other populations (Salvi and Tuberosa, 2005). For primary QTL mapping, Monte Carlo simulations have shown that at least 200 individuals from the segregated population are required. For higher resolution, as required for positional cloning, progenies of several thousand plants are needed. For example, in the Alpert and Tanksley´s work in 1996 more than 3,400 individuals were analyzed to obtain a detailed map around a fruit weight locus in tomato (Meksem and Kahl, 2005).
As an alternative to positional cloning, QTL may be determined using association mapping. This method allows identifying a statistic association between markers or candidates loci and the overall of an analyzed phenotype within a set of genotypes (natural populations, germplasm accessions and cultivars). It is important that the plant collection contains a wide spectrum for the trait to evaluate, and in particular it is an advantage for the analysis if the collection shows up extreme phenotypes (Meksem and Kahl, 2005; Salvi and Tuberosa, 2007).
Five main steps exist for the association studies: 1) selection of the population's samples, 2) determination of the level and influence of the structure population on the sample, 3) phenotypic characterization of the population for the interest trait, 4) population genotyping for regions/candidate genes candidates or as a whole genome scan, 5) assessment of the association between genotypes and phenotypes. The selection of the association test is the last step and it depends on the population's characteristics. Association mapping uses ancestral recombination and genetic natural diversity within a population to analyze quantitative traits and it is built on the base of the LD concept.
It is used to think that the terms linkage and linkage disequilibrium have similar meanings. However, although they are related, genetic linkage makes reference to the correlated inheritance of two loci through several generations because the two loci is at a sufficiently short physical distance that recombination meiotic events do not show up, and selection acts in the same way over the two loci, whereas LD refers to the identical frequency in the presence of two alleles of different loci inside a population, and this non-random association can be caused by other factors than linkage (Flint-Garcia et al., 2003; Gebhardt et al., 2004; Gupta et al., 2005).
Contrary to linkage mapping, where the genetic maps are created using generations of well characterized pedigrees generated from simple or multiple crossings, the LD based association studies can rely on the variation generated by the segregation in natural populations of non related individuals (Gaut and Long, 2003; Ersoz et al., 2007). It is expected that the period of time until the most recent common ancestor between two non related individuals of a population is bigger than the time presented by a population generated by a crossing, for this cause the samples used in LD mapping present more informative meiosis, generated through history, than the meiosis showed up in a traditional population mapping (Gaut and Long, 2003). Meiosis is considered informative when effective recombinations are generated, sending information from one genetic pool to other genetic pool. In this way ancestral recombinations can capture mixing between different populations and within this when LD is present this is important for the association assessment.
Some statistical tests used in association mapping
Factors that affect LD
LD is affected by biological factors, as the recombination and the allelic frequencies, and for historical factors that affect population size, like the selection, and bottlenecks with extreme genetic drift, selection for or against a phenotype controlled by two non linked loci (epistasis). Mating patterns and gene flow between individuals of genetically distinct populations followed by intermating can strongly influence LD (Buckler and Thornsberry, 2002).
LD decreases faster in outcrossing species than selfing species, this is due to less effective recombination in selfing species where the individuals are more likely to be homozygous than in outcrossing species (Flint-Garcia et al., 2003; Gaut and Long, 2003; Gupta et al., 2005).
In presence of a high LD a low density of markers is required in a target region. With low LD, many markers are required but the diagnostic markers resolution is higher, potentially until the level of the gene or of QTN (i.e. the quantitative trait nucleotide polymorphism responsible for the QTL effect). It is expected high variable levels of LD through the genome due to variations in recombination rates, presence of hot spots and selection, variation in recombination rate is a key factor that contributes to the variance observed in LD patterns (Salvi and Tuberosa, 2007).
Possible complications to measure LD and therefore to carry out the association mapping, can show up due to structure population in the studied sample. The influence of structure population depends on the relationships among sampled individuals. So, populations to be employed in an association study should be classified according to the sample individual relationship. Structure population can generate statistically significant but invalid biologically associations (Ersoz et al., 2007).
Low LD levels are expected when the population is diverse and the common ancestor within the individual population is too far in time, also low LD is not distributed uniformly along all the genome and it is located in short distances around specific loci, which produce only significant cooccurrences among physically near loci, increasing mapping resolution (Flint-Garcia et al., 2005).
Breeding, crop domestication and a limited genetic flow in many wild plant species have generated erosion processes and genetic drift that have produced structured populations (i.e. populations with allelic frequencies differences among sub-populations). These populations generate not functional significant associations among loci or between a marker and a phenotype, even without marker physically binding to the responsible locus for phenotypic variation (Ersoz et al., 2007).
However, different methods have already been generated; these methods make it possible to interpret results of association tests, controlling statistically the effects of stratified populations, because association studies that do not keep in mind the effects of structure population must be viewed with skepticism (Flint-Garcia et al., 2003). All these methods are based on the use of independent marker loci to detect and correct stratified populations.
LD measurement
In statistics LD can be conceived as a covariance measure of two molecular markers polymorphisms or as the non-random association between allelic states in pairs of loci, with biallelic or multiallelic loci.
If one locus has alleles A and a with pA and 1-pA frequencies, and a second locus has alleles B and b with pB and 1-pB frequencies, thus in equilibrium, even though the loci are linked, the expected haplotype frequencies are the product of constituent allele frequencies, for example using the AB
haplotype: pAB = pAxpB (1)
When this expression is true for all the alleles in the loci, it is said that the population is in linkage equilibrium. In a statistical context it is said that association between A and B does not exist. The basic component of all LD statistical tests is the difference between observed (pAB) and expected haplotype frequencies (pA x pB ) (Gaut and Long, 2003). Any departure from this state of linkage equilibrium is defined as:
DAB = pAB - pAxpB (2)
Being DAB the two loci coefficient of LD. For example: Considering two sets of single nucleotide polymorphisms (SNPs) in eight individuals (Ind) in four different situations:
It is necessary to notice that the absolute value of D is symmetrical and it does not care which allele is measured and associated.Situation 2) randomized data, implying recombination between sites.
Situation 3) unequal marginal frequencies between sites that do not imply that recombination has occurred; C may be a relatively new mutation that occurred on the T background
Situation 4) complete disequilibrium with change in allelic frequencies.
D incorporates information about association and allelic frequencies, but it can be difficult to interpret, because is highly dependent from the allele frequency. Although the two places are still in complete disequilibrium the change in the allele frequencies A and G takes to a value of D = 0.109. This value is different to the value found in situation 1 (D = 0.25). Due to this dependence on allele frequency, it is expected that the values of D vary thoroughly over many couples of SNPs even when the places are in complete LD. There are two ways to control D dependence on marginal allelic frequencies. The first way is ignoring low frequency variants. In some cases frequencies lower than 5 or 10 percent are ignored. The second solution is using rescaled measurements of D respect to the observed allelic frequencies, the most common measurements are D' and r2 (Gaut and Long, 2003).
D' varies in a range between 0 and 1, even if allelic frequencies differ among loci (Jorde, 2000). D' is calculated as:
As it can be observed in the previous situation D', contrary to D, shows that loci is in LD. D' can only be smaller than 1 if all the four possible haplotypes are observed, thus it is expected that an recombination event has happened between the two loci when D' is smaller than 1 (Flint-Garcia et al., 2003).
The r2 is considered as the square of the correlation coefficient between the two loci. It assumes a value of 1 if only two haplotypes are present (i.e. a value of 1 is possible only if the two loci have identical allelic frequencies). r2 such as D are dependent on allele frequency (Oraguzie et al., 2007).
So, r2 is D2 divided for the product of the two loci allelic frequencies:
Although r2 and D' behave extremely well with small sample sizes and/or low allele frequencies, each measure presents different advantages. The r2 summarizes mutational and recombinational history while D' only measures the recombinational history and it is, therefore, the most exact statistic to estimate differences in recombination. However to smaller sample sizes, the probability of finding the four allelic combinations diminishes. In low frequencies it is the way even if the loci are not linked. The great advantage of the statistical r2 is that it can indicate how the markers can be correlated with interested QTL (Flint-Garcia et al., 2003; Oraguzie et al., 2007).Some researchers have focused over the distance which r2 overall is reduced to 10% as the least reasonable point of LD for complex traits associations. The reason for this value is that for a complex trait a QTL can explain approximately 10% of phenotypic variation. If a marker only explains 10% of the QTL, then the marker will explain only 1% of the phenotypic variation. The detection of locus effects that cause a phenotypic variation as lower as 1% requires an exponential increment of the population size, therefore these little effects could be considered undetectable in a moderate population size (Ersoz et al., 2007).
For measuring the overall LD between the two multiallelic loci, one modification of D (D') is widely used (Zapata, 2000).
The LD statistical significance can be tested using 2 x 2 contingency tables and the independence between two loci may be tested using a chi squared goodness of fit test or using a Fisher exact test (Gupta et al., 2005).
Methods for analysis of structure population and association mapping
Genomic control approach
The genomic control (GC) method is used in case-control studies which adjust the variance of a trend test by use of data from null loci. The GC of Devlin and Roeder (1999) uses the Cochran-Armitage (CA) trend tests, because, in contrast to allele-based tests, like ?2 test for association, they are valid when Hardy-Weinberg equilibrium does not hold. To apply the CA trend test, increasing scores are assigned a priori to the genotypes. Choice of scores depends on the underlying genetic model (recessive, additive or dominant), the Devlin and Roeder GC test use optimal scores for the additive model (Devlin and Roeder, 1999; Zheng et al., 2006).
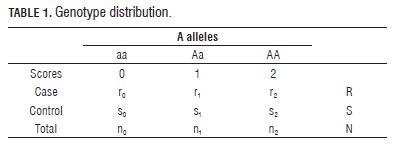
For a case-control study and "n" biallelic markers, the data for each marker are given in a standard 2 x 3 table of genotypes by case and control (Tab.1), where ri (si ) i = 0, 1, 2 is the number of cases (controls) whose genotypes have i A alleles.
The CA trend test is based on the test statistic:
Under Ho of no association between trait and marker; E(U) = 0. CA trend test can be written (Sasieni, 1997) as:
Where xi are the scores; xi can be chosen such that this statistic is locally most powerful for detecting particular types of associations. For example, in order to test whether allele a is dominant over allele A, the choice x = (1, 1, 0) is locally optimal. To test whether allele a is being recessive to allele A, the optimal choice is x = (1, 0, 0). To test whether alleles a and A are codominant, the choice x = (0, 1, 2) is locally optimal. For complex diseases, the underlying genetic model is often unknown (Devlin and Roeder, 1999). When there is no population substructure or cryptic relatedness, for a given x, Z2(x) asymptotically follows a chisquared distribution with one degree of freedom under the null hypothesis of no association between the disease and the gene (Sasieni, 1997). Thus, the null hypothesis is rejected when Z2(x)> ?2. To adjust for population substructure or cryptic relatedness, Devlin and Roeder (1999) propose a new test statistic
Where, Λ(1) is the variance inflation factor that can be estimated using the null loci, Devlin and Roeder (1999) using Bayesian and frequency approaches define Λ(1) as:
where 2 2 1 (1),..., (1) c Z Z are the trend tests calculated on c null loci. These null loci are assumed to be unrelated to the trait and segregate independently, and the effect of population substructure on them is similar to that at the trait locus. Zheng et al. (2006) showed the optimal tests for the recessive and dominant models.
is approximately distributed 2 1 under the null hypothesis, but a Bonferroni correction provides a conservative critical value for the test 2 1 ( c) (Devlin and Roeder, 1999). The test adapts and corrects for problems arising from population heterogeneity. The disadvantages of this test: poor choice of controls, and cryptic relatedness of cases, are presented when dealing with complex diseases because the underlying genetic models (additive, dominant or recessive) are usually unknown and the test may lose substantial power when the model is misspecified (Zheng et al., 2006).Structured association
Like GC, structured association uses additional markers randomly distributed across the genome, but, in contrast to GC where the aim is to estimate the amount of genetic differentiation among the unobserved populations, the interest of this method is the assignment of individuals to populations. This method first, needs to know how many populations are in the study sample, and if unknown, these populations are estimated using model-based methods, assuming that each population is modeled by a characteristic set of allele frequencies. Having estimated the population structure, the association test is made. This test, named structured population association test (STRAT), replaces the standard null hypothesis (no association between allele frequencies at the candidate marker and trait), with a null hypothesis of no association between subpopulation allele frequencies at the candidate locus and phenotype, versus an alternative hypothesis where the subpopulation allele frequencies at the candidate locus depends on phenotype (Pritchard et al., 2000a).
There are three parameters in the model: X, Z and P. X denotes the genotypes of the sampled individuals. The genotyping is made using unlinked marker loci that might be a series of randomly chosen markers from across the genome and the unlinked marker loci would include the candidate loci themselves.
Z denotes the (unknown) population of origin of the individuals. P denotes the (unknown) allele frequencies in all populations. The main modeling assumptions are Hardy-Weinberg equilibrium within populations and complete linkage equilibrium between loci within populations. The model could be without admixture (if each individual is assumed to originate in one of K populations) or with admixture. Given the origin population of each individual, the genotypes are assumed to be generated by drawing alleles independently from the appropriate population frequency distribution that completely specifies the probability distribution Pr(X| Z, P).
To perform inference for Z and P, the method adopts a Bayesian approach, having observed the genotypes (X), the knowledge about Z and P is given by the posterior distribution:
An approximate sample (Z(1), P(1)), (Z(2), P(2)), , (Z(M), P(M)) is obtained using Markov Chain Monte Carlo methods (MCMC), and inference for Z and P may then be based on summary statistics obtained from this sample, the number of populations (K) is also inferred for MCMC methods. All the algorithms for the MCMC methods are running using the software STRUCTURE that divides individuals into populations. The individuals can be assigned to more than one population if their genotypes indicate that they are admixed. This method can produce highly accurate assignments using modest numbers of loci. All the test is based on the idea that any association between a candidate allele and the phenotype within a subpopulation cannot be due to population structure (Pritchard et al., 2000b). After allocation of individuals to populations, the test for association is carried out in a model fitting exercise. The trait is regressed on the estimated coefficients of population membership and then on the marker studied (Mackay and Powell, 2007).Implications for a research looking for identification of molecular markers associated to polygenic traits through trait-marker association Association studies have several advantages regarding positional cloning. While mapping with positional cloning can take among 5 to 10 years to get the necessary resolution, by means of association mapping it can take three to 5 years. In an association mapping study some of the results can be immediately employed in markers-assisted plant breeding. Since the resolution could lead to markers that are highly linked with the trait under evaluation.
With association mapping it is not necessary to produce populations derived of controlled mattings and natural populations, wild species and breeding lines can be used to build the research population.
Association mapping permits to observe multiple loci and to use the accumulated variation obtained from n meiotic generations in order to get bigger mapping resolution than the resolution reached by the use of positional cloning. The limitation of the association mapping method is, when the population is structured and there is a high LD, then false associations can be done and the mapping can show low resolution. To compensate these limitations genomic control and structure association are robust methods to evaluate the association between markers and traits controlling structure population problems.
Association mapping is mainly a five step methodology useful to find QTL, also exhorts the importance of diversity in genetic studies. The understanding of LD is fundamental for the concept of association mapping and is a requisite for successful association studies. Even though that the statistical treatment of the association might be complex the reduction in time and its efficiency is supported in the number of publications using this method.
Conclusions and perspectives
Association genetics started as a strategy for plant studies since 2001 with the a candidate gen approach in maize (Thornsberry et al., 2001), but genome wide association studies were not used until 2008, in potato using AFLP markers (D'hoop et al., 2008). Much finer studies of genome wide association approach were done with SNP markers, especially for the species for which the genome is available.Rice genome sequence was published on 2002, the first association studies were published on 2007 (Agrama et al., 2007) and 2009 (Yan et al., 2009) barley is one example (Cockram et al., 2010). At least 20 association studies had been done in different crop and non crop species, mixed between candidate gene approach and genome wide association approach. This fact demonstrates that association studies are a real and useful tool for QTL analysis and discovery. Considering that new technologies for high throughput sequences have been developed and their costs have diminished and for the other side, high throughput technologies to analyze and characterize phenotypes are being developed, this allows to measure complex traits in accurate way and to find connections between genomics data with phenotypic data. All of these developments contribute to precision breeding and to use effectively the huge amount of information derived from genome sequences.
Literature cited
Abdurakhmonov, I.Y. and A. Abdukarimov. 2008. Application of association mapping to understanding the genetic diversity of plant germplasm resources (online). Int. J. Plant Genomics, http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2423417/; consulted: November, 2011. [ Links ]
Agrama, H.A, G.C. Eizenga, and W. Yan. 2007. Association mapping of yield and its components in rice cultivars. Mol. Breeding 19(4), 341-356. [ Links ]
Buckler, E.S. and J.M. Thornsberry. 2002. Plant molecular diversity and applications to genomics. Curr. Opin. Plant Biol. 5(2), 107-111. [ Links ]
Chakraborty, R. and K.M. Weiss. 1988. Admixture as a tool for finding genes and detecting that difference from allelic association between loci. PNA 85, 9119-9123. [ Links ]
Cockram, J., J. White, D.L. Zuluaga, D. Smith, J. Comadran, M. Macaulay, Z. Luo, M.J. Kearsey, P. Werner, D. Harrap, C. Tapsell, H. Liu, P.E. Hedley, N. Stein, D. Schulte, B. Steuernagel, D.F. Marshall, W.T. Thomas, L. Ramsay, I. Mackay, D.J. Balding, A. Consortium, R. Waugh, and D.M. O'Sullivan. 2010. Genome-wide association mapping to candidate polymorphism resolution in the unsequenced barley genome. PNAS 107(50), 21611-21616. [ Links ]
D'hoop, B.B., M.J. Paulo, R.A. Mank, H.J. Van Eck, and F.A. Van Eeuwijk. 2008. Association mapping of quality traits in potato (Solanum tuberosum L.). Euphytica 161(1), 47-60. [ Links ]
Devlin, B. and K. Roeder. 1999. Genomic control for association studies. Biometrics 55(4), 997-1004. [ Links ]
El-Assal, S.E.-D., C. Alonso-Blanco, A.J. Peeters, V. Raz, and M. Koornneef. 2001. A QTL for flowering time in Arabidopsis reveals a novel allele of CRY2. Natl. Genet. 29(4), 435-440. [ Links ]
Ersoz, E.S., J. Yu, and E.S. Buckler. 2007. Applications of linkage disequilibrium and association mapping in crop plants. pp. 97-119. In: Varshney, R.K. and R. Tuberosa (eds.). Genomics-assisted crop improvement. Springer, Dordrecht, The Netherlands. [ Links ]
Flint-Garcia, S.A., J.M. Thornsberry, and E.S Buckler. 2003. Structure of linkage disequilibrium in plants. Annu. Rev. Plant Biol. 54(1), 357-374. [ Links ]
Flint-Garcia, S.A., A.-C.Thuillet, J. Yu, G. Pressoir, S.M. Romero, S.E. Mitchell, J. Doebley, S. Kresovich, M.M. Goodman, and E.S. Buckler. 2005. Maize association population: a high-resolution platform for quantitative trait locus dissection. Plant J. 44(6), 1054-1064. [ Links ]
Gaut, B.S. and A.D. Long. 2003. The lowdown on linkage disequilibrium. Plant Cell 15(7), 1502-1506. [ Links ]
Gebhardt, C. 2004. Potato genetics: molecular maps and more. Molecular marker system in plant breeding and crop improvement. pp. 215-227. In: Lörz, H. and G. Wenzel (eds.). Biotechnology in Agriculture and Forestry. Vol. 55. Springer, Berlin. [ Links ]
Gebhardt, C., A. Ballvora, B. Walkemeier, P. Oberhagemann, and K. Schüler . 2004. Assessing genetic potential in germplasm collections of crop plants by marker-trait association: a case study for potatoes with quantitative variation of resistance to late blight and maturity type. Mol. Breeding 13, 93-102. [ Links ]
Gebhardt, C., L. Li, K. Pajerowska-Mukthar, U. Achenbach, A. Sattarzadeh, C. Bormann, E. Ilarionova, and A. Ballvora. 2007. Candidate gene approach to identify genes underlying quantitative traits and develop diagnostic markers in potato. Crop Science 47, 106-111. [ Links ]
Gupta, P.K., S. Rustgi, and P.L. Kulwal. 2005. Linkage disequilibrium and association studies in higher plants: Present status and future prospects. Plant Mol. Biol. 57, 461-485. [ Links ]
Jorde, L.B. 2000. Linkage disequilibrium and the search for complex disease genes. Genome Res. 10(10), 1435-1444. [ Links ]
Kruglyak, L. 1999. Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Natl. Genet. 22, 139-144. [ Links ]
Mackay, I. and W. Powell. 2007. Methods for linkage disequilibrium mapping in crops. Trends Plant Sci. 12(2), 57-63. [ Links ]
Meksem, K. and G. Kahl. 2005. The handbook of plant genome mapping. Wiley-VCH, Weinheim, Germany. [ Links ]
Oraguzie, N.C., E.H.A. Rikkerink, S.E. Gardiner, and H.N. De Silva. 2007. Association mapping in plants. Springer, New York, NY. [ Links ]
Pritchard, J.K., M. Stephens, N.A. Rosenberg, and P. Donnelly. 2000a. Association mapping in structured populations. Amer. J. Hum. Genet. 67(1), 170-181. [ Links ]
Pritchard, J.K., M. Stephens, and P. Donelly. 2000b. Inference of population structure using multilocus genotype data. Genetics 155(2), 945-959. [ Links ]
Risch, N. and K. Merikangas. 1996. The future of genetic studies of complex human diseases. Science 273, 1516-1517. [ Links ]
Salvi, S. and R. Tuberosa. 2005. To clone or not to clone plant QTLs: Present and future challenges. Trends Plant Sci. 10(6), 297-304. [ Links ]
Salvi, S. and R. Tuberosa. 2007. Cloning QTLs in plants. pp. 207-225. In: Varshney, R.K. and R. Tuberosa (eds.). Genomics-assisted crop improvement. Springer, Dordrecht, The Netherlands. [ Links ]
Sasieni, P.D. 1997. From genotypes to genes: Doubling the sample size. Biometrics 53(4), 1253-1261. [ Links ]
Sattarzadeh, A., U. Achenbach, J. Lübeck, J. Strahwald, E. Tacke, H.- R. Hofferbert, T. Rothsteyn, and C. Gebhardt. 2006. Single nucleotide polymorphism (SNP) genotyping as basis for developing a PCR-based marker highly diagnostic for potato varieties with high resistance to Globodera pallida pathotype Pa2/3. Mol. Breeding 18, 301-312. [ Links ]
Simko, I., S. Costanzo, K.G. Haynes, B.J. Christ, and R.W. Jones. 2004a. Linkage disequilibrium mapping of a Verticillium dahliae resistance quantitative trait locus in tetraploid potato ( Solanum tuberosum) through a candidate gene approach. Theor. Appl. Genet. 108(2), 217-224. [ Links ]
Simko, I., K.G. Haynes, E.E. Ewing, S. Costanzo, B.J. Christ, and R.W. Jones. 2004b. Mapping genes for resistance to Verticillium albo-atrum in tetraploid and diploid potato populations using haplotype association test and genetic analysis. Mol. Genet. Genomics 271, 522-531. [ Links ]
Simko, I., K.G. Haynes, and R.W. Jones. 2006. Assessment of linkage disequilibrium in potato genome with single nucleotide polymorphism markers. Genetics 173, 2237-2245. [ Links ]
St. Clair, D.A. 2010. Quantitative disease resistance and quantitativeresistance Loci in breeding. Annu. Rev. Phytopathol. 48, 247-268. [ Links ]
Thornsberry, J.M., M.M. Goodman, J. Doebley, S. Kresovich, D. Nielsen, and E.S. Buckler. 2001. Dwarf8 polymorphisms associate with variation in flowering time. Natl. Genet. 28(3), 286-289. [ Links ]
Yan, W., Y. Li, H.A. Agrama, D. Luo, F. Gao, X. Lu, and G. Ren. 2009. Association mapping of stigma and spikelet characteristics in rice (Oryza sativa L.). Mol. Breeding 24(3), 277-292. [ Links ]
Zapata, C. 2000. The D' measure of overall gametic disequilibrium between pairs of multiallelic loci. Evolution 54(5), 1809-1812. [ Links ]
Zheng, G., B. Freidlin, and J.L. Gastwirth. 2006. Robust genomic control for association studies. Amer. J. Hum. Genet. 78(2), 350-356. [ Links ]