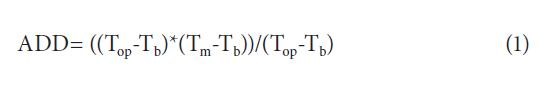Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Agronomía Colombiana
versão impressa ISSN 0120-9965
Agron. colomb. v.29 n.3 Bogotá set./dez. 2011
PROPAGATION AND TISSUE CULTURE
Phyllochron and differential growth between plants of French tarragon (Artemisia dracunculus L.) with different source of propagation
Filocrono y crecimiento diferencial entre plantas de estragón (Artemisia dracunculus L.) con diferente origen de propagación
John Cristhian Fernández-Lizarazo1,3, Teresa Mosquera-Vásquez2, Bernardo Chaves2 and Felipe Sarmiento2
1Agricultural Engineering Programme, Faculty of Agricultural Sciences, Universidad de La Salle. Yopal (Colombia).2Department of Agronomy, Faculty of Agronomía, Universidad Nacional de Colombia. Bogota (Colombia).
3Corresponding author. jhcristhian@gmail.com Received for publication: 22 April, 2010. Accepted for publication: 2 November, 2011.
ABSTRACT
French tarragon is included within the brochure of herbs that Colombia is offering to export. Although renewal is recommended every three or four years, in Colombia there are crops more than eight years of age and with low yield because its traditional vegetative propagation is difficult, therefore it is necessary to establish alternative propagation methods to improve its yield. In order to analyze the phyllochron and growth between French tarragon plants with different origin of propagation (micropropagation and traditional propagation), parameters to simulate field behavior from a model was estimated. From cardinal temperatures, a quadratic function of tarragon's phyllocron, whose rate was higher in plants from micropropagation during establishment, was determined. The general meristematic activity in plants of in vitro treatment shown to be greater than plants of field treatment, as well as leaf area index (LAI), fraction of intercepted light (FLINT) extinction coefficient (K) and radiation use efficiency (RUE), which involved differences in the architecture of plants in both treatments. Distribution of biomass to leaves and stems was similar in both treatments. This is the first study using a deterministic model to analyze the effect of micropropagation in field tarragon's growth.
Key words: radiation use efficiency, growth model, growth rates, cardinal temperatures.
RESUMEN
Estragón está en el portafolio de hierbas aromáticas para exportación que ofrece Colombia. Aunque se recomienda su renuevo cada tres o cuatro años, en Colombia hay cultivos de más de ocho años de edad y con bajo rendimiento, por cuanto su propagación vegetativa tradicional es difícil, por lo tanto es necesario establecer métodos alternativos de propagación para mejorar su rendimiento en campo. Con el objetivo de analizar el filocrono y el crecimiento entre plantas de estragón con diferente origen de propagación (micropropagación y propagación tradicional), se estimaron los parámetros para simular su comportamiento en campo a partir de un modelo. A partir de las temperaturas cardinales, se determinó que el filocrono de estragón obedeció a una función cuadrática cuya tasa fue mayor para las plantas provenientes de micropropagación. Adicionalmente, la actividad meristemática general de las plantas provenientes de micropropagación mostró ser mayor, así como el índice de área foliar (IAF), fracción de luz interceptada (FLINT), coeficiente de extinción (K) y uso eficiente de la radiación (UER), lo que implicó diferencias en la arquitectura de estas plantas. Esta es la primera investigación que utiliza un modelo determinístico para analizar el efecto de la micropropagación en el crecimiento en campo de estragón.
Palabras clave: uso eficiente de la radiación, modelo de crecimiento, índices de crecimiento, temperaturas cardinales.
Introduction
Tarragon is a perennial, creeping, herbaceous plant with alternate leaves of linear shape and light green color (Morales, 2008). Under tropical conditions the plant does not flower, while in its place of origin, Russia and Siberia, it produces flowers but sterile seed (Bareño, 2006). This happens as a consequence of meiotic alterations during microsporogenesis (Rousi, 1968). In Colombia tarragon is cultivated in open grounds from 0-1,800 m a.s.l. and from 1,900-2,800 m a.s.l. under greenhouse conditions (Bareño and Clavijo, 2006).
Tarragon is propagated by rooted cuttings or by rhizome division (Mackay and Kitto, 1988). although it is difficult to achieve rooting. Consequently, in Colombia there are tarragon crops with more than eight years of age, even though renewal is recommended every three or four years (Small and Deutsch, 2001; Bareño and Clavijo, 2006), which reduces its yield. Currently, there is a need of establishing alternate methodologies for tarragon propagation, as part of the strategies to optimize its yield.
Crop modeling has become an important tool both in research and in other areas of production focused on solving operational problems in the field, especially taking into account climate change indicating the richness and versatility of this technique (Gary et al., 1998). Crop modeling is a valuable low cost tool that generates results in little time (Pereyra and Aguirrezábal, 2007) and provides quantitative information from which decisions can be taken for productive system management that ranges from planting date to crop protection (Gary et al., 1998).
A model is an abstraction of an existing system, or a system that could become real. Its aim is to explain a system and predict its responses so that it can be managed (Lentz, 1998). Mathematical models in plant physiology can be divided into empirical (descriptive) and causal (mechanistic), the latter based on physiological processes (Garbeya et al., 2006; Prusinkiewicz, 1998; Hunt, 1982). Empirical models represent the data acquired from a convenient and useful to make predictions based on interpolation practices of such data.
Empirical models represent data acquired in a convenient way, and are useful for practical predictions based on data interpolation. In contrast, mechanistic models follow the traditional reductionist model of natural sciences and give explanations and answers that integrate the mechanism and contribute to understand any studied process (Prusinkiewicz, 1998).
This research analyzed the phyllochrom and growth between tarragon plants (Artemisia dracunculus L.) from different propagation origins through a model.
Materials and methods
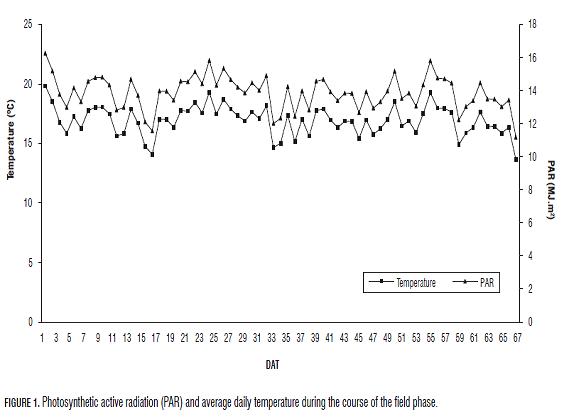
The investigation was carried out in the production greenhouses of the Agronomy School of the Universidad Nacional de Colombia (Bogota), located at 2,556 m a.s.l. with coordinates 4°35'56.57" N. Relative humidity was 42%, average temperature of 16.94°C and average photosyntetically active radiation (PAR) was 11.22 MJ m-2 (Fig.1).
Two treatments were evaluated: first, plants coming from micropropagation (M) and second plants coming from conventional propagation (CP). M plants were obtained from rooted cuttings of micropropagated plants previously hardened in a propagation greenhouse. CP plants were obtained from rooted cuttings of plants in a production greenhouse. Micropropagation protocols, micropropagated plantlets-hardening protocols and shoot rooting protocols were described previously (Fernández, 2009).
Planting was performed in a 20 m2 soil-bed divided into two plots (treatments), each of 10 m2, with a plant density of 160,000 plants/ha. Irrigation was 2 L m-2 and fertilization was done according to soil analysis (Tab.1), referring to N: 250 kg ha-1; P2O5: 100 kg ha-1; K2O 120 kg ha-1 (Arjona, 2006). This is the same procedure performed for tarragon cultivation in the greenhouses of the Faculty of Agronomy of the Universidad Nacional de Colombia, Bogota. Management of pests and diseases was timely done according to populations, levels and symptoms.
Phyllochron
The phyllochron parameter, or thermal time between the appearance of two successive tarragon leaves (= 1cm) was determined by calculating the accumulated degrees per day with the following formula (Dellai et al., 2005):
Where ADD are the accumulated degrees-day, Top and Tb are the optimal and base temperatures of tarragon respectively, and Tm is the mean daily field temperature. Tm was measured in 1 h intervals with a datalogger 3M® located at 25 cm above ground.The Top and Tb were previously determined in the lab from a non-linear regression from the daily foliar emission rate at 10.5°C, 13.5°C, 18.8°C, 22.7°C and 35°C. For this a Lab-Line ® growth chamber was used, and 28 in vitro rooted and homogenous plants sown in nine flasks per temperature. The maximal growth temperature (Tmax) was also estimated but it was not included in the ADD formula since temperatures above this value were never registered in the field.
Growth model
A multiplicative deterministic model that simulates daily growth rate and biomass distribution per organ was developed to analyze plant growth. To accomplish this, plant material was harvested each two weeks from the tenth day after transplanting (dat) until day 67, for a total of four evaluations. Leaf area was measured with a planimeter LI-COR 3000®. Leaf and stem biomass was determined after drying the material at 104°C for 24 h until a constant weight.
The components of the model were: photosynthetically active radiation (PAR) in MJ, intercepted light fraction (FLINT) and radiation efficient use (RUE) in mg MJ-1. The PAR during the experiment was obtained from the daily sunshine hours transformed according to Angstrom (1924) and the FLINT was determined according to Spitters et al. (1989):
Where K is the light extinction coefficient and LAI is the leaf area index, which was calculated as the coefficient between the leaf area and the ground surface unit (Hunt, 1978). Estimation of RUE and K parameters, biomass distribution coefficient per organ, daily growth rate (g m-2 d-1), daily total dry matter, and its distribution per organ were done according to Salazar et al. (2008).Growth analysis
Total dry matter, foliar dry matter and foliar area simulated by the model described above were modeled empirically, and from these values, next instantaneous values were derived according to Hunt (1978): leaf area ratio (LAR), specific leaf area (SLA), net assimilation rate (NAR), relative growth rate (RGR), absolute growth rate (AGR) and crop growth rate (CGR).
Results
Phyllochron
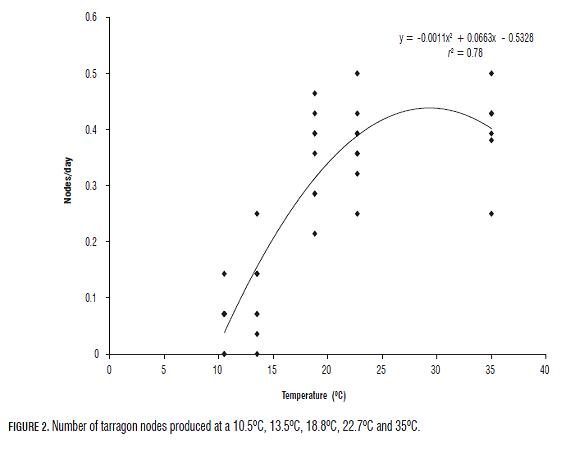
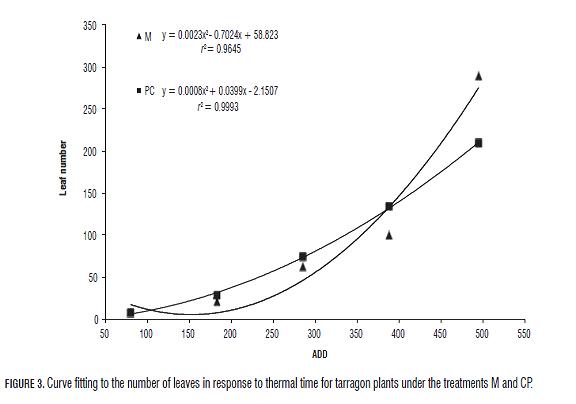
Daily foliar emission rate (measured as nodes/day), used for the determination of cardinal temperatures, displayed a quadratic curve (y = ax2 + bx + c) with r2 = 0.78 (Fig.2). The optimal temperature (Top) was determined by deriving the equation and equaling it to zero; the value was 30.1364°C. The base and maximal growth temperatures (Tb and Tm respectively) were calculated equaling "y" to zero; the resulting values were 9.5491°C and 50.7237°C respectively. According to this, in spite of not testing higher temperatures and if the response is completely quadratic, it is expected that at 50.72°C the growth of tarragon ceases. The field comparison of the two evaluated treatments showed that the number of leaves produced by M and CP plants with respect to accumulated degrees per day (ADD) described quadratic curves with an estimated r2 of 0.9645 and 0.9993 respectively (Fig.3). The phyllochron or thermal time between the appearance of two successive leaves (= 1cm) did not present a constant value for either treatment. However, from the 248 ADD (31 dat), the rate of plant leaf emission M exceeded the CP plants (Fig.3) and the derivative or daily rate of leaf showed a slope lower in CP plants (0.0016) than in M plants (0.0046).
Growth model
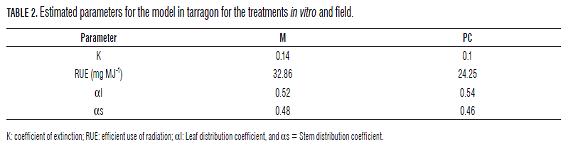
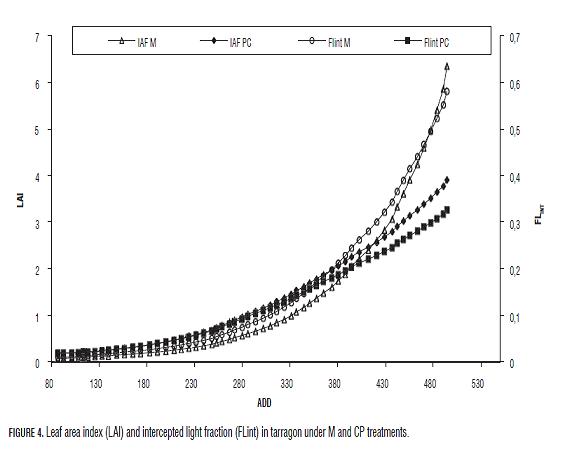
During this investigation no asymptotic LAI or FLINT values were observed for any treatment (Fig.4). Nonetheless, maximal LAI and FLINT values for M plants (6.3524 and 0.5811 respectively; Fig.4), almost doubled the same values obtained for CP plants (3.9102 and 0.3261 respectively; Fig.5). Moreover, the functional curve form for both treatments was similar. Both K and RUE values presented higher values in M plants (Tab.2). Th e leaf and stem dry mass distribution coeffi cients were similar and showed a higher proportion of assimilates in leaves than in stems.
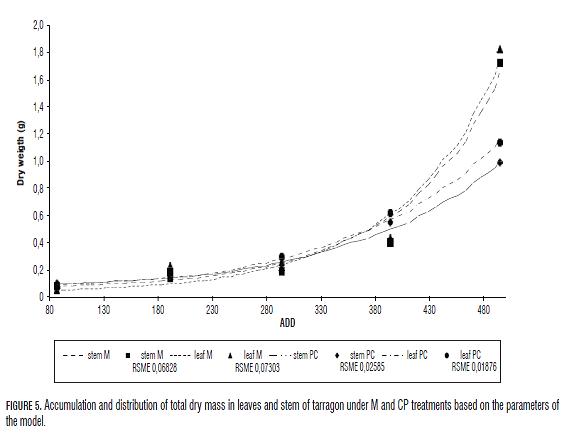
Leaf and stem dry mass accumulation curves in M and CP plants displayed similar tendencies with root mean square error (RMSE) close to zero, which indicate a good adjustment of the simulated data for aerial parts (Fig.5). Th e dry mass of the root was not taken into account because it is diffi cult the complete extraction of roots from the ground, and there could be a source of variation between treatments and even among plants.
Th e accumulated dry mass in the aerial part of the plants was similar until the 394 ADD (52 dat). However, the fi nal dry mass in stems was higher in M plants (1.72 g) than in CP plants (0.99 g). Moreover, fi nal dry mass in the leaves of M plants (1.82 g) was higher than in CP plants (1.14 g). Th e fi nal dry weight for the aerial parts for M plants was of 3.54 g while for CP plants were 2.13 g. All total dry mass and dry foliar mass values simulated by the model, as for foliar area, adjusted to exponential models, except for foliar area of CP plants that adjusted to a quadratic model. Th e r2 in all cases was 0.99, which evidences good data adjustment. Th e growth indexes were derived from the adjusted simulated data.
Growth analyses
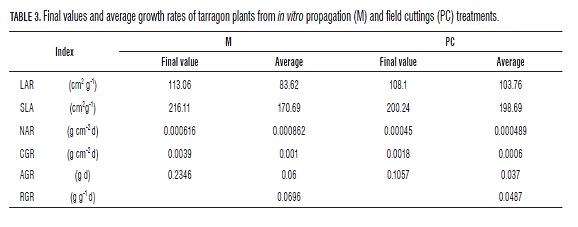
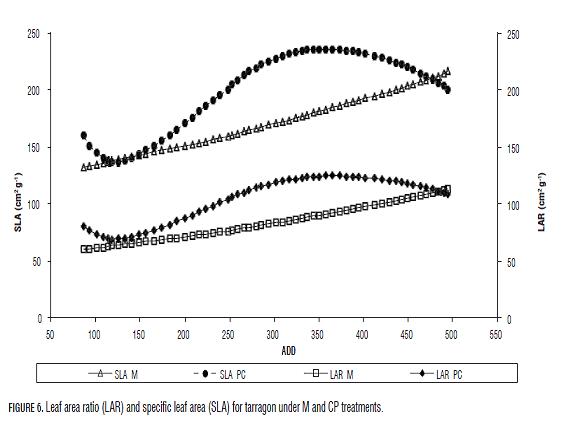
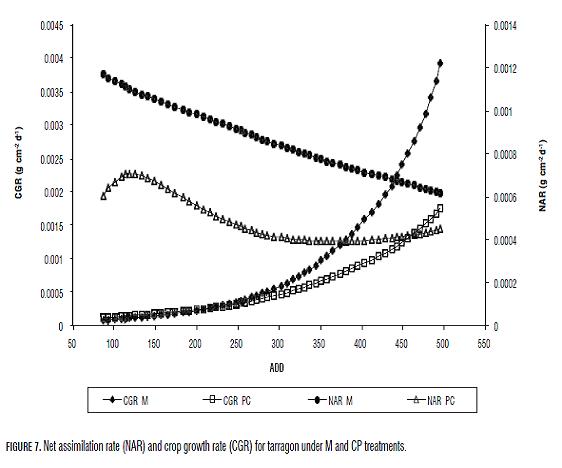
Plants' LAR and SLA in both treatments displayed a tendency towards increment through thermal time. Th ermal time values were lineal for M plants (Fig.6). LAR and SLA values for CP plants had a minimal value at 118 ADD (15 dat) (LAR 68.90 cm2 g-1 and SLA 136.37 cm2 g-1) and a maximal at 357 ADD (47 dat) (235.87 cm2 g-1) for LAR and at 365 ADD (48 dat) for SLA (124.29 cm2 g-1). Despite that end values of LAR and SLA were higher in M plants its average values were lower compared to CP plants (Tab.3). RGR for plants under both treatments was constant throughout the data gathering time. M plants had a RGR of 0.0696 g g-1 d-1 and CP plants had a RGR of 0.0487 g g-1 d-1. Th is is a constant value because in y= e(B*(X-C)) exponential curve, the "B" value corresponds to RGR as constant value. Plants' NAR in both treatments had a descending tendency, more constant for M plants (Fig.7). For CP plants, NAR incremented until 0.00071 g cm-2 d-1 when the plants accumulated 118 ADD (15 dat). In spite of this, M plants had a higher average and fi nal NAR than CP plants (Tab.2, Fig.7).
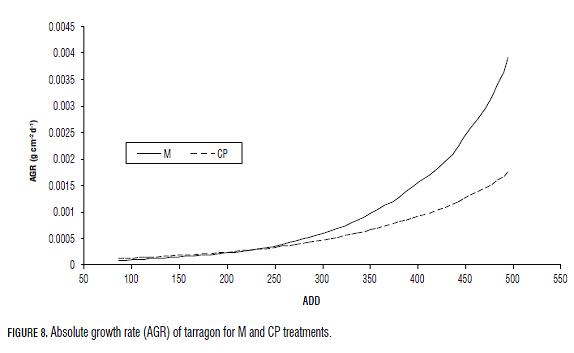
Th e CGR tendency for plants under both treatments was similar until 231 ADD (30 dat), when its values were around 0.0003 g cm-2 d-1. Th e average and maximal CGR registered for M plants were higher than for CP plants (Tab.3, Fig.7). Th e AGR for plants under both treatments incremented in time and was similar for the plants until 248 ADD (31 dat) where its value was of 0.02 g d-1 (Fig.8). Aft erwards, the AGR in M plants incremented in a higher proportion than that of CP plants (Tab.3, Fig.8).
Discussion
This study developed the first guidelines for prediction, under different environments, of the response of tarragon plants in the field to propagation methods applied. This was achieved through the development of a tarragon potential growth model, without water or nutrient limitation, or dry mass reduction because of pests or sicknesses. Taking into account that metabolic and cell division and elongation processes are temperature-dependent (Yuan and Bland, 2004), data are presented based on degrees per day or physiological time because, in general terms, enhances the adjustment and gives better growth parameter estimates (Tei et al., 1996).
Phyllochron
Cardinal temperatures were determined based on the foliar emission rate using in vitro plants grown in a phytotron. To date, according to the literature, neither cardinal temperatures, nor the methodology developed for tarragon research have previously been reported. The obtained values for Tb (9.5491°C), Tmax (50.7237°C) and Top (30.1364°C) (Fig.2), are consistent with the corresponding temperatures at the height above sea level where tarragon growth in the field is possible in Colombia, this is between 0 and 1,800 m a.s.l. (Bareño, 2006). The minimal and maximal temperatures for these regions are around 12.5 and 38°C respectively, and it is possible to record temperatures of 52°C at ground level (Humboldt and Bonpland, 1985).
The applied methodologies using a mathematical approach from data obtained in the field or from physiological simulations of data obtained with a phytotron (Pulido, 2008), with plants grown in soil, do not allow full control of additional variables such as plant homogeneity, nutrition, water availability, topographical conditions, pests, sicknesses, vapor pressure deficit and radiation. In contrast, in this report, the highly controlled conditions that offered the sowing pots and the phytotron, as the plant homogeneity, allowed a better control of these variables which constitutes an advantage of the method.
However in an effort to optimize the adopted methodology in this study, it would be important to develop protocols that include plants of a similar size as the ones normally used in the field. In this sense, Pietka (1998) states that the outlining of standard environmental conditions play an important role in the theoretical analysis of plant growth and in its practical application.
The phyllochron has been estimated as a constant value in several species (Bassu et al., 2008; Dellai et al., 2005; Ishag et al., 1998), in a similar way non-linear functions have been determined (Kovács, 2005). The tarragon phyllochron was described with quadratic curves in both treatments during the measured period (Fig.3), which might be explained by the fact that the phyollochron depends on the genotype (Ishag et al., 1998), or because this characteristic was estimated during its establishment phase which involved initially a transplantation from the propagation greenhouse to its final place in the field (Bareño, 2006). This implies that root manipulation and root hair loss could have brought an initial water stress in both treatments even though water supply was optimal.
During water stress, abscisic acid levels increase, which might induce, among others, dormancy and/or an increase in the root/shoot rate (Nielsen and Orcutt, 1996). For tarragon, this could mean an increase in assimilate translocation to the root, especially given its tendency to rhizome formation. The initial low leaf number, which could have increased exponentially as the plants overcame the initial water stress, could have caused a variable phyllochron number. However, the magnitude of a possible water stress was not tested and it should be subject of further studies. In wheat, the phyllochron interval is also affected by water stress and temperature (Baker, 1986).
The M plants came from environments with a high relative humidity under in vitro and propagation greenhouse conditions, which may have affected the amount of leaf cuticle and made them more susceptible to a higher transpiration. Indeed, loss of turgency and leaf death was observed, accompanied by the growth of new leaves that support the initial growth and production of more leaf area, which required more time. Despite of the possible higher transpiration in M plants, the increase in the leaf emission rate starting from 248 ADD (Fig.3) above CP plants, showed a better resilience and a higher meristematic activity in the shoot.
Growth model
The FLINT is profoundly related with the leaf area index that was bigger for M plants, although no asymptotic values were calculated (Fig.4). Tarragon is a plant of continuous growth in the tropics and extremely sensitive to the environmental conditions (Rutskikh et al., 1998). Tarragon is also a "ramet" type plant, with a strong tendency to axillary shoot and rhizome development, which makes maximal FLINT value susceptible to change depending on the field conditions. That is why the maximal FLINT must be analysed in detail in further investigations
The LAI and the FLINT were higher for M plants, not only because of its higher leaf emission rate, but also because there were more branches per plant that, for M plants, were 21.6 branches against 13.6 for CP plants at the end of the measurements. The branches as a whole might be considered a reflection of a particular meristematic activity state (Prusinkiewicz, 1998). This suggests that the meristematic activity of M plants is much higher than in CP plants.
"Ramet" type plants such as tarragon have a reiterative programmed activation of apical and/or axillary meristems (Zang et al., 2002). This program was faster in M plants, which translated in an incremented LAI and a change in the plant architecture concerning light capturing and extinction through the canopy (Salazar, 2008). In consequence, there were differences in light distribution in the canopy between plants of both treatments (Ruíz and Bertero, 2008), and a higher extinction coefficient (K) for M plants (0.14) than for CP plants (0,10) (Tab.2). However further research must be carried out to study plant architecture based in other parameters, such as leaf and branch angle in longer time frames and different sowing densities.
The RUE was relatively low in both treatments (Tab.2) compared with broccoli (228 mg MJ-1), cabbage (118 mg MJ-1) (Carranza et al., 2008), cape gooseberry (460 mg MJ-1) (Salazar et al., 2008) and Mitostachys mollis (6,220 mg MJ-1), estimated by the same methodology (Suarez, 2009). This was due to the low sowing density (160,000 plants/ha), the small size of the plants and that there was no competition between them (Salazar, 2008). Furthermore, the RUE varies between crops and varies with cultural practices (Rosati and Dejong, 2003); its values could also vary depending on the radiation intensity and temperature (Olesen and Grevsen, 1997). Because of the total incident PAR is a function of location, year, planting date and crop phenology (Ruiz and Bertero, 2008) is important to validate the tarragon model in other locations and planting dates. Meanwhile, M plants had higher K values (resource capture) and RUE (transformation of the resource) (Tab.2), indicating greater efficiency in the conversion of photoassimilates.
Growth analysis
Overall, both the LAR and SLA, CP plants showed two points of accumulation of reserves of assimilates in stem and possibly in root from transplant until 118 ADD (15 dat) and from the 357 ADD (47 dat) onwards, and also a clear trend of assimilate distribution to increase leaf area between these points. By contrast, M plants showed constant distribution of assimilate values towards increased leaf area (Fig.6).
NAR indicates the photosynthetic efficiency of plants. The tendency of NAR in plants of both treatments is to decrease (Fig.7), due, firstly, to the relative capacity of daily production respecting to existing leaf area is lower and secondly to self-shadowing. Despite this, NAR values were higher in M plants (Fig.7).
NAR has a constant tendency in M plants and a variable tendency in CP plants. In the latter, NAR increases may be associated with the distribution of assimilates to storage organs such as root or stem, which in some species, is related to the increase of photosynthetic activity (Midmore et al., 2007).
Additionally, the inverse relationship between SLA and NAR (Figs. 6 and 7) suggests that there was a process of assimilates accumulation in leaves, variations in the level of light interception and reduction of the photosynthetic apparatus per unit area when the SLA was higher (Jaimez et al., 2008; Liu et al., 2007), which could be compensated by increases in leaf area (Richards, 2000). However CP plants had lower rates of leaf emission and leaf area than M plants; therefore its NAR and consequently its RUE were lower. The translocation of resources ramet-plants like tarragon, is highly dependent on environmental conditions, developmental state (Wang et al., 2004; Li et al., 2008), i.e. mothers, daughters or granddaughters plants and is also genetically determined (Liu et al., 2007). However, these patterns of distribution are not yet completely clear. The slight NAR increase and the decrease in the values of the LAR and the SLA at the end of the period measured in CP plants indicates dry matter accumulation in leaves and stems and reflects a different physiological age, given their tendency to store assimilates contrary to the M plants whose tendency is to invest assimilates constantly in leaf area, which may be evidence of juvenility at a physiological level, although this requires further investigation.
An index that can reflect the juvenility of the plant material coming from in vitro propagation is the RGR, because it indicates the efficiency of the plants to produce biomass with respect to the existing (Hunt, 1978). Moreover, it is regarded as a crucial value in mechanistic models (Tei et al., 1996).
For plants under both treatments the RGR showed constant values. However, in M plants, the RGR was higher than in CP plants. The close relationship between the LAR, RGR and NAR, (Gary et al., 1998; Hunt, 1982), and the highest values of these ratios in M plants suggest greater vigor in terms of leaf area and biomass production, which is reflected on AGR (Fig.8), which increases substantially from the 248 ADD (31 dat), and coincides with the point at which the leaf emission rate of M plants exceeds that of the CP plants (Fig.3).
CGR (Fig.7), which is the product of LAI and NAR (Hunt, 1982) reflects a similar behavior to AGR (Fig.8). Nevertheless, the difference between the magnitudes of both treatments is evident from the 231 ADD (30 dat), which coincides with the point at which the negative slope of the NAR of both treatments has its greatest separation (Fig.7), i.e. the point at which the reduction of photosynthetic efficiency of CP plants is greater than that of the M plants. According to the literature review to date, there has not been reported the use of empirical or deterministic models to analyze the growth of plants in field previously propagated in vitro. This is the first report that uses a deterministic model to analyze the effect of in vitro propagation in growth and biomass distribution of tarragon.
Literature cited
Arjona, H. 2006. Fisiología de la nutrición vegetal en frutas y hortalizas. In: Últimas tendencias en hierbas aromáticas culinarias para exportación en fresco. Faculty of Agronomy, Universidad Nacional de Colombia, Bogota. [ Links ]
Baker, J.T., P. Printer, R. Reginato, and E.T. Kanemasu. 1986. Effects of temperature on leaf appearance in spring and winter wheat cultivars. Agron. J. 78, 605-613. [ Links ]
Bareño, P. 2006. Estragón (Artemisia dracunculus). pp. 97-99. In: Últimas tendencias en hierbas aromáticas culinarias para exportación en fresco. Faculty of Agronomy, Universidad Nacional de Colombia, Bogota. [ Links ]
Bareño, P. and J. Clavijo, 2006. Hierbas aromáticas culinarias para exportación en fresco In: Últimas tendencias en hierbas aromáticas culinarias para exportación en fresco. Faculty of Agronomy, Universidad Nacional de Colombia, Bogota. [ Links ]
Bassu. S., S. Asseng, R. Motzo, and F. Giunta. 2008. Optimising sowing date of durum wheat in a variable Mediterranean environment. Field Crops Res. 111(1-2), 109-118. [ Links ]
Carranza, C., O. Lanchero, D. Miranda, M. Salazar, and B. Chavez. 2008. Modelo simple de simulación de masa seca en brócoli (Brassica sp.) variedad coronado y repollo (Brassica oleraceae) híbrido Delus cultivados en la sabana de Bogotá. Agron. Colomb. 26 (1), 23-31. [ Links ]
Dellai, J., G. Trentin, D. Bisognin, and N. Streck. 2005. Filocrono en diferentes densidades de plantas de batata. Ciênc. Rural 35(6), 1269-1274. [ Links ]
Fernández, J. 2009. Evaluación del efecto de la micropropagación en el enraizamiento y producción de biomasa de estragón (Artemisia dracunculus Linn.) en campo a través de un modelo de crecimiento. M.Sc. thesis. Faculty of Agronomy, Universidad Nacional de Colombia, Bogota. [ Links ]
Gamba, Y. and N. Ramírez. 2006. Aspectos biológicos de la roya del estragón Puccinia tanaceti D.C. var. dracunculina (Fahrend) Cummins. Undergraduate thesis. Faculty of Agronomy, Universidad Nacional de Colombia, Bogota. [ Links ]
Garbeya, C., M. Garbey, and S. Mullera. 2006. Using modelling to improve models. Ecol. Mod. 197, 303-319. [ Links ]
Gary, C., J. Jones, and M. Tchamitchian. 1998. Crop modelling in horticulture: state of the art. Sci. Hortic. 74, 3-20. [ Links ]
Humboldt, A. and A. Bonpland. 1985. Geografía de las plantas. Jardín Botánico José Celestino Mutis, Bogota. [ Links ]
Hunt, R. 1978. Plant growth analysis. Edward Arnold Publishers, London. [ Links ]
Hunt, R. 1982. Plant growth curves: The functional approach to plant growth analysis. Edward Arnold Publishers, London. [ Links ]
Ishag, H., B. Mohamed, and K. Ishag. 1998. Leaf development of spring wheat cultivars in an irrigated heat-stressed environment. Field Crops Res. 58, 167-175. [ Links ]
Jaimez, R., N. Santos, B. Añez, J. Vásquez, and W. Espinoza. 2008. Photosynthesis of field-grown Arracacha (Arracacia xanthorriza Bancroft) cultivars in relation to root-yield. Sci. Hortic. 118, 100-105. [ Links ]
Kage, H. and H. Stützel. 1999. A simple empirical model for predicting development and dry matter partitioning in cauliflower (Brassica oleracea L. botrytis). Sci. Hortic. 8, 19-38. [ Links ]
Lentz, W. 1998. Model applications in horticulture: a review. Sci. Hortic. 74, 151-174. [ Links ]
Li, P., N. Wang, W. He, B. Krüsi, S. Gao, S. Zhang, F. Yu, and M. Dong. 2008. Fertile islands under Artemisia ordosica in inland dunes of northern China: Effects of habitats and plant developmental stages. J. Arid Environ. 72, 953-963. [ Links ]
Liu, F., J. Liu, F. Yu, and M. Dong. 2007. Water integration patterns in two rhizomatous dune perennials of different clonal fragment size. Flora 202, 106-110. [ Links ]
Mackay, W. and S. Kitto. 1988. Factors affecting in vitro shoot proliferation of french tarragon. HortScience 113, 282-287. [ Links ]
Midmore, D.J. 2007. Review of physiology of crop production. pp. 405-406. In: Fageira, N.K., V.C. Baligar, and R.B. Clark (eds.). Experimental agricultura. Haworth Press. New York, NY. [ Links ]
Morales, A.J. 2008. Biogeografía y aprovechamiento de la flora autóctona valenciana: el caso de las plantas aromáticas, medicinales y condimentarias. In: Facultad de Geografia e Historia, Universidad de Valencia, http://site.ebrary.com/lib/unalbogsp/ Doc ?id=10204172&ppg=267; consulted: November, 2011. [ Links ]
Nielsen, E. and D. Orcutt. 1996. Physiology of plant under stress, abiotics factors. John Wiley & Sons, New York, NY. [ Links ]
Olesen, J. and K. Grevsen. 1997. Effects of temperature and irradiance on vegetative growth of cauliflower (Brassica oleracea L. botrytis) and broccoli (Brassica oleracea L. italica). J. Exp. Bot. 48, 1591-1598. [ Links ]
Pereyra, G. and L. Aguirrezábal. 2007. Sunflower yield and oil quality interactions and variability: Analysis through a simple simulation model. Agr. Forest Meteorol. 143, 252-265. [ Links ]
Pietka, J. 1998. Plant growth influenced by photosynthetic irradiance and temperature Part I: Mathematical model for standard conditions. BioSystems 45, 11-20. [ Links ]
Pulido, S. 2008. Desarrollo de un modelo fenológico de lulo (Solanum quiétense var. septentrionales Lam.). M.Sc. thesis. Faculty of Agronomy, Universidad Nacional de Colombia, Bogota. [ Links ]
Prusinkiewicz, P. 1998. Modelling of spatial structure and development of plants: a review. Sci. Hortic. 74, 113-149. [ Links ]
Richards, R. 2000. Selectable traits to increase crop photosynthesis and yield of grain crops. J. Exp. Bot. 51, 447-458. [ Links ]
Rosati, A. and T. Dejong. 2003. Estimating photosynthetic radiation use efficiency using incident light and photosynthesis of individual leaves. Ann. Bot. 91, 869-877. [ Links ]
Rousi, A. 1968. Cytogenetic comparison between two kinds of cultivated tarragon (Artemisia dracunculus). Hereitas 10, 194-213. [ Links ]
Rutskikh, I., M. Khanina, E. Serykh, L. Pokrovsky, and A. Tkachev. 1998. Chemical composition of essential oil of Artemisia dracunculus L. from Siberia. Chemistry of Plant Raw Material 4(3), 65-76. [ Links ]
Salazar, M., J. Jones, B. Chaves, and A. Cooman. 2008. A model for the potential production and dry matter distribution of cape gooseberry (Physalis peruviana L.). Sci. Hortic. 115, 142-148. [ Links ]
Small, E. and G. Deutsch. 2001. Herbes culinaires pour nos Jardins de Pays Froid. NRC Research Press, Ottawa. [ Links ]
Spitters, C., H. vab-Keulen, and D. Van-Kraalingen. 1989. A simple and universal crop growth simulator: SUCROP87. pp. 107-122. In: Rabinge, R., S. Ward, and H. Van Laar, (eds.). Simulation and system management in crop protection. Pudoc, Wageningen, The Netherlands. [ Links ]
Suárez, D. 2009. Análisis de crecimiento y composición de aceites esenciales en plantas de minthostachys mollis en dos ambientes contrastantes. M.Sc. thesis. Faculty of Agronomy, Universidad Nacional de Colombia, Bogota. [ Links ]
Tei, F., A. Scaife, and D. Aikman. 1996. Growth of lettuce, onion and red beet. 2. Growth modelling. Ann. Bot. 78, 645-652. [ Links ]
Yuan F. and W. Bland 2004. Light and temperature modulated expolinear growth model for potato (Solanum tuberosum L.). Agric. Forest Meteorol. 121, 141-151. [ Links ]
Wang, Z., L. Li, X. Han, and M. Dong. 2004. Do rhizome severing and shoot defoliation affect clonal growth of Leymus chinensis at ramet population level? Acta Oecol. 26, 255-260. [ Links ]
Zhang, C., C. Yang, and M. Dong. 2002. The significance of rhizome connection of semi-shrub Hedysarum leave in an Inner Mongolian dune, China. Acta Oecol. 23, 109-114. [ Links ]