Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Agronomía Colombiana
Print version ISSN 0120-9965
Agron. colomb. vol.32 no.3 Bogotá Sept/Dec. 2014
https://doi.org/10.15446/agron.colomb.v32n3.45627
Doi: 10.15446/agron.colomb.v32n3.45627
1 Forest Hydrology and Watershed Management, Water Center for Latin American and the Caribbean, Monterrey Institute of Technology and Higher Education. Monterrey (Mexico). jnavar@itesm.mx
Received for publication: 19 September, 2014. Accepted for publication: 17 November, 2014.
ABSTRACT
This study reports a set of robust regional M-tree allometric equations for Mexico's tropical dry forests and their application to a forest inventory dataset for the States of Durango and Sinaloa, Mexico. Calculated M data from 15 reported equations were fitted, applied and validated for regional and global models. Proposed theoretical models, empirically derived equations, as well as global and local reported equations were fitted and applied to calculated M-tree data using wood specific gravity, diameter at breast height, and top height as exogenous variables. Empirically-derived, computer-based equations assessed the M-tree evaluations slightly better than the theoretical, the global and the local models. However, the theoretical models projected compatible M-tree values and deserve further attention once wood specific gravity data are collected in the field. Using the best fit equation, mean M plot density values of 30, 41 and 35 Mg ha-1 were estimated from 57 plots (1,600 m2 each), 217 plots (1,000 m2 each) and 166 plots (1,000 m2 each) in the tropical dry forests of the States of Durango, Tiniaquis and Vado Hondo (Sinaloa), respectively. The large sample size, the richness of the tested allometric models, the economic and ecological importance of this data-source, and the spatial coverage of these equations made this dataset uniquely useful for biomass, charcoal, and other bio-energy estimations, as well as for understanding the inherent heterogeneity of the stand-structure in dynamic tropical forest environments.
Key words: biomass and Bio-fuels, theoretical and empirical equations, global equations for tropical trees, forest inventory.
RESUMEN
Este estudio reporta un conjunto de ecuaciones alométricas robustas para la evaluación de M de los bosques tropicales secos de México y su aplicación al inventario forestal para los estados de Durango y Sinaloa, México. Los datos calculados de M de 15 ecuaciones reportadas se ajustaron, aplicaron y validaron ecuaciones regionales y mundiales. Los modelos teóricos propuestos, las ecuaciones empíricamente derivadas, así como también las ecuaciones derivadas local y mundialmente se ajustaron y aplicaron para evaluar M con el uso de la gravedad específica de la madera, el diámetro normal y la altura total como variables exógenas. Las ecuaciones empíricamente derivadas computaron ligeramente mejor M que los modelos teóricos, las ecuaciones locales o mundiales. Sin embargo, los modelos teóricos proyectaron valores comparables de M y merecen atención adicional una vez que la gravedad específica de la madera sea medida en campo. Con el uso de la mejor ecuación ajustada, los valores promedio de M al nivel del sitio fueron de 30, 41 y 35 Mg ha-1, los cuales se estimaron para 57 (1.600 m2 cada uno); 217 (1.000 m2 cada uno) y 166 (1.000 m2 cada uno) sitios del inventario forestal en los bosques tropicales secos del Estado de Durango y los ejidos de Tiniaquis y Vado Hondo (Sinaloa), respectivamente. El tamaño de muestra grande, la riqueza de los modelos alométricos probados, la importancia económica y ecológica de esta fuente de datos y la cobertura espacial de estas ecuaciones hacen de este conjunto de datos y ecuaciones útiles para la estimación de biomasa, combustibles y carbón vegetal y bioenergía así como también para entender la heterogeneidad inherente de la estructura de los bosques tropicales.
Palabras clave: Biomasa y bio-combustibles; ecuaciones teóricas y empíricas, ecuaciones mundiales para bosques tropicales, inventario forestal.
Introduction
The development and application of allometric equations are the standard methodology for estimating tree, plot, regional, and global aboveground forest biomass (Brown, 1997; Chave et al., 2005). Currently, aboveground biomass assessments are central to the evaluation of the amount of bio-energy contained in biomass as a partial alternative to fossil fuels in the clean and sustainable production of energy (Mckendry, 2002). Current interest in biomass research centers for global environmental issues related to forest ecosystems contributes to the global carbon and nitrogen cycles and aids in mitigating the potential effects of climate change (Canadell and Raupach, 2008). Aboveground evaluations are also essential to estimating other biomass components since M correlates well with belowground biomass root stocks as well as with litter and necromass stocks (Cairns et al., 1997; Mokany et al., 2006). The assessment of aboveground biomass helps in understanding resource allocation theories for tree organs. Currently, two theories coexist: optimal and allometric resource allocation (West et al., 1999).
Aboveground biomass equations can be classified according to the spatial scale on which trees are harvested. Local, site-specific M-tree equations often cover small areas and they frequently evaluate the M-tree of single tree species. This situation typically arises in the case of plantations composed of high-value tree species or when precise estimates are needed locally for research and environmental management. A great deal of examples using these mathematical models were compiled and reported for tree species from Latin America by Návar (2009a). General pan tropical, non-site-specific allometric equations usually traverse geographical boundaries but they are usually developed for single tree species. Examples have been reported for Eucalyptus tree species of Australia and Pinus massoniana trees for southern China (Montagu et al., 2005; Williams et al., 2005; Xiang et al., 2011). Regional aboveground biomass equations encompass all tree species of an ecosystem and usually cover broader spatial areas of interest. The case of structurally complex, diverse, and natural forests that have many tree species with different wood specific gravity values, bole forms, branching patterns, etc. is particularly addressed by these equations. Brown (1997) and Chave et al. (2005) reported allometric examples for tropical dry, moist and rain-forests. The M-tree for Mexico's western tropical dry forests was reported by Martínez-Yrizar et al. (1996).
Regional equations are a cost-effective estimation of the M-tree and M plot and related variables at multiple sites and species across the geographical range of the distribution of an ecosystem. Data collected from the national forest inventory can be more precisely converted into biomass, bio-energy, carbon or nitrogen stocks with the use of regional pan tropical, allometric equations. Pan tropical, regional equations simplify the long-term inventory measurements into M estimates and allow more resources to be focused on the extension of such inventories (Williams et al., 2005). Conventional and environmental projects require these sources of information as well. The calculation of the M-tree of species lacking biomass allometry in the forest inventory is also simplified with pan tropical, regional equations. The global equations of Brown et al. (1989); Brown (1997) and Chave et al. (2005) are classic in a great deal of conventional and environmental studies, with the main assumption that these equations evaluate the M-tree well for any tree of any tropical forest. However, non-regional applications have been rarely tested.
It is then highly likely that global or site-specific equations are biased towards regional or national M assessments (Chave et al., 2005; Houghton, 2005). In light of this literature review, the primary objectives of this research were: (i) to construct empirical regional allometric equations, (ii) to apply more theoretical models, (iii) to validate empirical and theoretical models, and (iv) to evaluate the M-stand for regional tropical forests of Durango and Sinaloa, Mexico. A total of 15 different allometric equations for Mexico's tropical dry forests and three forest inventory datasets for the tropical dry forests of Durango and Sinaloa, Mexico, as well as 30 M-tree data values for Puerto Rican tropical dry forests were available for accomplishing these objectives. The testing hypothesis was that any theoretical and empirical equation would equally fit the M-tree data. Therefore, any single equation could be applied to the forest inventory datasets.
Materials and methods
Tropical dry forests of Mexico
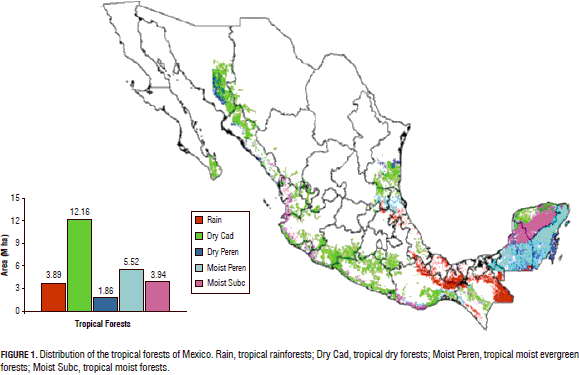
The tropical dry forests of Mexico are distributed in the lowlands paralleling the Pacific Ocean Coast, the Caribbean Sea, and the Gulf of Mexico. They are classified as tropical dry forests spanning an area of between 15 to 18 -million ha, covering nearly 9% of the Mexican territory (Palacio-Prieto et al., 2000). These forests cover large extensions from Sonora and Chihuahua to Chiapas. Some remnant forests and several elements of these forests are also distributed on the Atlantic Coasts, including the Yucatan Peninsula (Fig. 1).
Allometric theory
Biomass equations can be classified into empirical, semi-empirical and theoretical models (Návar, 2010). Empirical equations most often fit parameters statistically by least square techniques in a regression analysis, although other techniques such as the power variance model, usually fitted, maximize the log-likelihood of nonlinear equations. Theoretical models physically parameterize equations that convey meaningful biomass descriptions. Semi-empirical models require both physically and statistically-calculated parameters. Theoretical and semi-empirical models project M for any tree of any species in any forest at any scale. Therefore, they can be contrasted with local, regional and global allometric equations.
The West et al. (1999) theoretical model
A fully, theoretical model proposed by West et al. (1999) was developed using the theory of fractals, hereafter referred to as the WBE model. The WBE framework is described with the following Eq. 1.
Where, C = a proportionality constant, D = diameter at breast height, and r = the specific gravity of the entire aboveground biomass. The scalar exponent, BWBE, is fixed at 8/3 = 2.67 and specific gravity is referred as the total tree specific gravity (a weighted average of wood, bark, branches and leaves).
The reduced Návar's (2010) non-destructive model
Návar (2010) proposed the following reduced, semi-empirical model, which is described by Eq. 2.
Model Eq. 2 can be described as fully theoretical by assuming that a = C × rw and finding correct values for C. The constant exponent value was derived from the meta analysis of allometric equations (Návar, 2010). In general, Návar (2010) found that C = 0.2457 for North American tree species.
Empirical equations
Návar (2010) reported the most-common empirical model for aboveground biomass estimations in the log-transformed Eq. 3.
where: a and B are the scalar intercept (a) and exponent (B) of equation [4], respectively; both parameters are calculated by least square techniques in log linear regression; ei = the error. Note that the a-scalar intercept of model [1]= Cr of the West et al. (1999) model and that BWBE = 2.67. Also note that Bw ≠ B.
Brown et al. (1989) and Chave et al. (2005), for tropical forests worldwide, and Návar (2010), for Mexico's northern temperate forests, proposed other empirical equations, which expanded on Eqs.1 and 2. Model Eq. 4 is an expansion of Eqs. 1 and 2.
where, H = tree top height.
Empirical or computer-based allometric models
Using the data matrix (M, D, H, and rw) for n number of trees to compute model coefficients is to let the computer choose those variables that explain the most M-tree variability using, for example, stepwise procedures (The SAS stepwise procedure selects only the variables that account for part of the model variability). These are empirical models in nature, although they contain variables that physically describe the mass of trees as variables selected by the SAS procedure that meet the probability requirements.
Aboveground biomass data
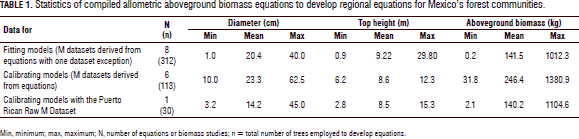
The tree allometry available for Mexico's tropical dry forest communities is reported in Tab. 1, which includes the number of compiled biomass equations (N), the number of trees harvested (n), the diameter and top height range. The wood specific gravity values for the tropical local species were collected from technical and scientific reports when this information was not reported. The top height data for the tropical dry tree species could not be collected. Hence, it was empirically derived from forest inventory studies.
Reported allometric equations
Most reported allometric equations are in the form of the conventional allometric model Eq. 4. Gómez-Díaz et al. (2011) constructed individual conventional equations for each of the following species: Acacia cochliacantha, Conzattia multiflora, Ipomoea arborescens, and Lysiloma microphyllum for the State of Morelos, Mexico. Martínez-Yrizar et al. (1996) reported a single equation that uses the wood specific gravity, the diameter at breast height and the top height as independent exogenous variables for Caesalpina erostachys, Apoplanesia paniculata, Lonchocarpus constrictus, Ipomoea wolcottiana, Lysiloma microphylla, Heliocarpus pallidus, Bursera excelsa, Caesalpinia sclerocarpa, Jatropha malacophylla, and Guettarda elliptica of Jalisco, Mexico. Návar (2009b) reported raw biomass data and a single equation for six Mexican Sinaloan tropical dry species: Acacia cochliacantha, Bursera penicillata, Lysiloma divaricata, Ceiba acuminta, Cochlospermum vitifolium, Jatropha angustifolia and Haematoxylon brasiletto. Cairns et al. (2000; 2003) reported a single equation as well as an equation for each of the following six tree species: Alseis yucatanensis, Brosimum alicastrum, Manilkara zapota, Pouteria campechiana, Pouteria unilocularis, and Trichilia minutiflora for the Yucatan Peninsula. A raw M dataset composed of 30 Puerto Rican tropical dry trees reported by Brandeis et al. (2006) was also available and it was used for validating the allometric equations. The validation procedure contrasts models by way of simulating data from equations and has some scientific value since it compares mean values rather than single independent M-tree data values.
Raw aboveground biomass data were available for the Sinaloan dry forest (Návar, 2009b) and for the Puerto Rican dry trees (Brandeis et al., 2006). Most often, biomass equations rather than raw M-tree data was collected. Therefore, M-D data pairs were projected using de reported equation with the reported diameter range and number of data values. Wood specific gravity values from scientific reports and internet sources was collected and completed the data matrix with these figures. The data matrix (M, D, H, rw) was split into fitting and validating datasets. Therefore, only descriptive statistics were reported and, since the bole volume was not available, the shape factor could not be objectively evaluated either, and hence only the theoretical and computer-based empirical equations were fitted to the M-tree data. The data were split into fitting (312 trees) and validating (113 trees) models for the Mexican, as well as for the 30 Puerto Rican, tropical dry trees reported by Brandeis et al. (2006) (Tab. 1).
For the M-tree data source, two theoretical models were fitted and seven computer-based, empirical equations and validated the applicability of the regional equation developed by Martínez-Yrizar et al. (1992) and the global equations reported by Brown et al. (1989) and Chave et al. (2005). The theoretical equations of West et al. (1999) and Návar (2010) tested the biomass data as well.
Applying aboveground allometric equations
In order to compute the density of the plot aboveground biomass stocks, the equation that better fit the M-tree data was applied to the measured D and H tree data recorded in the Mexican forest inventory dataset for the period 2004-2006 that was available for the State of Durango, Mexico as well as for the commercial forest inventory datasets collected for two public lands spaces of Sinaloa, Mexico. For the former plot data source, only tropical dry forest dendrometric data were employed.
Univariate statistics (mean, standard deviation, skewness, and the Weibull probability density function) are reported for plots encompassing each of the two tropical dry forest communities - Sinaloa and Durango, Mexico. This data source will eventually be employed along with a Geographic Information System to calculate the regional (Statewide) aboveground biomass stocks as well as the belowground (roots), litter, and necromass compartments using reported expansion factors.
Procedure
The WBE (Eq. 1) and Návar's (2010) reduced model preliminarily used the C value calculated for North American tree species. The empirical equations were fitted using stepwise procedures in linear and logarithmic-transformed fashions, and a combination of both. The variables that met the probability (P=0.05) requirements to be part of the equation were isolated and the coefficients were recalculated using either linear or log transformed models. Allometric equations of Martínez-Yrizar et al. (1996), Brown (1997) and Chave et al. (2005) were straightforwardly applied to the biomass data since they contained reported coefficients. All of the equations calculated the M-tree in conventional, standard units for comparisons of goodness of fit statistics. The standard error, Sx, the standard error in percentage, Sx(%), and the coefficient of determination, r2, are quality statistics reported for each allometric equation for fitting and validating allometric equations. Validation was conducted for Mexico's tropical dry forests as well as for the Puerto Rican tropical dry forests.
Results
Fitting and validating allometric equations
Table 2 depicts the allometric equations and quality statistics for fitting and validating the M-tree data. As expected, the theoretical WBE and Návar's (2010) reduced models did not account for any amount of M-tree variability and showed the largest standard errors (732% and 183% and 828% and 167% for fitting and validating the M-tree datasets, respectively) because the C coefficient value used was developed for temperate tree species (C = 0.2457). The second equation of Chave et al. (2005) for dry forests is also notoriously biased towards M-tree data with a Sx(%) of 175% and 138% for fitting and validating the datasets, respectively. The rest of the allometric equations generally fit the data well and, in most cases, more than 67% of the observed M-tree variation was explained by the exogenous variables employed.
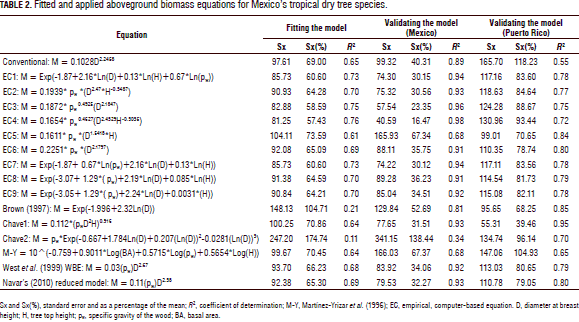
The empirical, computer-based equations fitted the collected M-tree data slightly better than the theoretical models (Tab. 2; Fig. 2). In general, the exogenous variables D, H, and rw accounted for most of the M-tree variation. The empirical, computer-based equations displayed acceptable and applicable statistics and they were able to exhibit most of the variation shown by the field data (Tab. 2; Fig. 2). However, the quality statistics increased notably for the validating models. In fact, Eq. 4 [0.1654* rw0.4627(D2.4329H-0.3035)] probably recorded the smallest Sx(%) (16%) of any allometric equation with this number of M-tree data that has ever been recorded (Tab. 2). This happened only for the Mexican tropical dry tree species. For the Puerto Rican tree species, the first equation of Chave et al. (2005) fitted the raw data better. The stepwise procedure in the linear and non-linear formats selected pw with an amount of variance explained at 4.2 and 3.7%, respectively, in contrast to the H variable which explained only 1.3 and 0.08% for fitting and validating Mexican datasets, respectively.
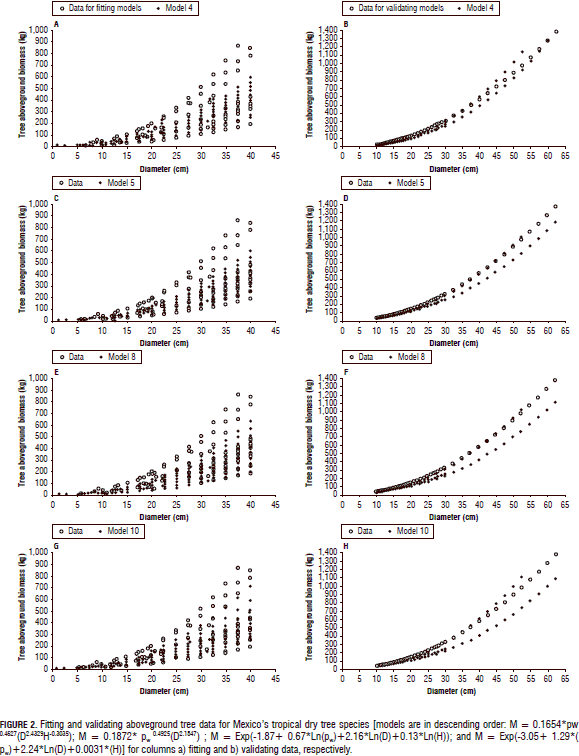
The empirical, regional M-tree Eq. 4 [M = 0.1654 * rw0.4627(D2.4329H-0.3035)] produced the best goodness of fit statistics since it had a 0.76 coefficient of determination and an Sx(%) of 57%; these fitness statistics were greatly improved for validating the Mexican dataset to 0.98 and 16%, respectively. Návar (2010) reported the local equation [M=0.08479(rw0.55255D2.2435H0.4773)] to have an r2 = 0.88 and Sx(%) = 39% for Mexico's Sinaloan eastern tropical forests. Martínez-Yrizar et al. (1996) reported an equation with an r2 value of 0.96. However, this last equation reproduced the M-tree with r2 and Sx(%) values of 0.64 and 70.4%, and 0.68 and 67.4% for fitting and validating the Mexican dataset, respectively.
The first equation of Chave et al. (2005), i.e. M = 0.112*(rw*D2*H)0.916, fitted the Mexican data well with intermediate goodness of fit statistics, r2 and Sx(%) values of 0.64 and 70.8(%) and 0.93 and 31.5(%) for fitting and validating the datasets, respectively. The Brown (1997) equation for Mexico's tropical dry trees did not reproduce the M-tree well with low goodness of fit statistics, r2 and Sx(%) values of 0.21 and 104.7% and 0.81 and 52.7% for fitting and validating the datasets, respectively.
All of the empirical, computer-based models validated the Mexican dataset well with r2 values > 0.91 and Sx values < 36.2(%). The theoretical models as well as the global first model of Chave et al. (2005) validated the dataset quite well as well, but with lower goodness of fit statistics of r2> 0.93 and Sx(%) < 34(%).
For the Puerto Rican dataset, the first model of Chave et al. (2005) was the only one with r2 and Sx(%) values of 0.95 and 39.5%, respectively. The rest of the models produced goodness of fit statistics with r2< 0.85 and Sx(%) > 68.3%.
Applying regional equations to the forest inventory dataset
The empirical, computer-based Eq. 4 [0.1654* rw 0.4627(D2.4329H-0.3035)] displayed acceptable and applicable statistics and recorded the smallest percentage of standard error (16%) of any allometric equation with this number of M data that has ever been recorded. This model estimated M plot densities for all three forest inventories. The estimated means (± standard deviation) of the M plot data for all three forest inventory datasets were 29.77 (± 26.88) Mg ha-1; 41.33 (± 31.47) Mg ha-1; and 35.32 (± 21.71) Mg ha-1 for Durango; Tiniaquis, Sinaloa; and Vado Hondo, Sinaloa, Mexico, respectively (Fig. 3). The M plot data was highly skewed (skewness coefficients of 2.05, 2.87, and, 0.87, respectively).
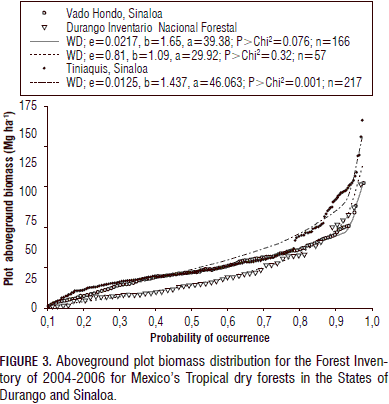
Discussion
The proposed regional allometric Eq. 4 was a satisfactory predictor of the M-tree and plot; furthermore, the total variation explained by the relationship was above 76%. The relationship was much stronger for the validating than for the fitting of the Mexican datasets because it accounted for 98% of the total M-tree variation. The single metric most commonly used for tree allometry is D, as is evident in the compilation of equations by Ter-Mikaelian and Korzukhin (1997); Jenkins et al. (2003); and Návar (2009a). For this dataset, in a linear and log-transformed fashion, D explained 0.62 and 0.92 of the total M-tree variability. However, conventional allometric models produce a mean M-tree estimator across D values and their application to groups of species is problematic for several reasons; the bole form-factor and wood specific gravity change with the tree species, sociological position, etc. Therefore, most current, empirical, modern, global models encompass the physical variables involved in tree mass assessments, such as form factors, wood specific gravity, and the volume usually given by D and H. Field bole volume data weighted by a form-factor (C) times specific gravity (rw) would eventually improve individual M-tree projections for any tree in any forest, as has been previously discussed above as well as reported by Brown et al. (1989); Chave et al. (2005) and Návar (2010). Unfortunately, at this time, there is not enough information to calculate shape factors and most reported rw data are often recorded for off-site trees, which vary greatly within the same tree and within the same tree species (Parolin, 2002; Chave et al., 2006). In addition, timber and branch volume equations are rarely integrated into a single bole component and expansion factors from timber to the full bole component usually come from off-site tree species that may have different branching patterns as well.
The original WBE (CrwD2.67) and Návar's (2010) reduced (CrwD2.38) theoretical models are biased towards the M-tree because the C coefficient was originally developed for temperate tree species. The preliminarily proposed C value was 0.2457 but this needs to be changed to 0.0395 in the WBE model in order to notably improve the fitting and validating quality statistics r2 and Sx(%) values of 0.68 and 66.2% and 0.92 and 34.1%, respectively. Návar's (2010) reduced model has to change the C coefficient value from 0.2457 to 0.1109 to notably improve the fitting and validating goodness of fit statistics r2 and Sx(%) values of 0.69 and 65.3%, and 0.93 and 32.2%, respectively. Návar's (2010) reduced model improved the goodness of fit statistics better than the WBE model. That is, a power figure of 2.38 appears to be more likely than a coefficient value of 2.67. In addition, the new C coefficient value for Návar's (2010) reduced model best resembles the 0.11 originally proposed for South East Asian tropical forests by Ketterings et al. (2001) and the new WBE C coefficient value is too small to obtain any physical interpretation.
The first Chave et al. (2005) equation could be regionally calibrated by fitting new equation coefficients [0.7702(rwD2H)0.6574] that recover the Sx (%) from 70.9% to 68.1% and the r2 from 0.64 to 0.67. The new Chave et al. (2005) equation's statistical parameters (0.7702 and 0.6574) appear to have statistical meaning only when allowing the intercept to remain constant; the new calibrated power equation parameter is 0.112[(rwD2H)0.865], which reproduces similar goodness of fit statistics. The power coefficient was shifted from the original 0.916 to 0.865, which would make sense considering the fact that Mexico's tropical dry forests may be found under drier conditions than the rest of the tropical dry forests of the world. Should this be the case, the power coefficient must be related to the annual rainfall, evapotranspiration, and water or energy balance for all tropical dry forests. Please note how Chave's et al. (2005) original, first equation, with a power coefficient value of 0.916, fits the Puerto Rican dataset well and it has to be changed to 0.865 for the Mexican dataset. Unfortunately, at this time, there are not sufficient data to test this hypothesis. Although fitness coefficients are not as good as those reported for other equations in Table 2, they would probably provide more consistent M-tree assessments than other empirical, proposed models, as was demonstrated by validating the Puerto Rican dataset. These issues are a matter for further research.
In general, there is a slight loss of precision when developing regional models from locally-developed or species-specific equations. For example, for the individual tree species of Mexico's western tropical dry forests, Martínez-Yrizar et al. (1996) reported values of 0.94 ≤ r2 ≤ 0.96. Gómez-Díaz et al. (2011) reported values of 0.88 ≤ r2 ≤ 0.99 for five tropical dry species of Morelos, Mexico. Návar (2010) reported a value of r2 = 0.88 for six of Mexico's Sinaloan tropical dry species. For this study, coefficient of determination values of 0.83 ≤ r2 ≤ 0.96 were expected when estimating the M-tree for any of Mexico's tropical dry trees. A small loss of precision is expected when estimating the M for tree species that belong to the plant community and lack biomass allometry. This often happens because of the calculation of the M-tree for unaccounted tree species in the development of allometric equations.
For local M-tree allometry, Cairns et al. (2003), for Mexican tropical dry trees, Youkhana and Idol (2011), for Hawaiian tropical agro-forestry trees, and Návar (2010), for Mexico's Sinaloan tropical dry trees, reported that the global models of Brown (1997) and Chavé et al. (2005) were consistently biased towards local tree and plot aboveground biomass assessments. Hence, there is a need for regionally calibrating global M-tree equations. The equation of Chave et al. (2005) and the equation of Brown (1997) had their global appropriateness for the Puerto Rican dataset tested since they resulted in the best goodness of fit statistics although they failed to reproduce similar goodness of fit statistics for the Mexican dataset. The rest of the developed and tested equations only reproduced intermediate fitting and validating statistics. Therefore, they are recommended for only calculating the M-tree, plot and region for the Mexican tropical dry forest communities. Evaluations of the M-tree for tropical dry forest communities beyond the Mexican climatic conditions may be biased.
Conclusions
This report aimed to fit theoretical models, build modern, empirical, regional, aboveground, biomass equations and contrast global equations for Mexico's tropical dry forests. In addition, the equation with the best goodness of fit statistics fitted the Mexican forest inventory data that was available for the State of Durango, Mexico as well as the two commercial forest inventory datasets available for Tiniaquis and Vado Hondo, Sinaloa, Mexico. The modern, computer-based equations that were built projected slightly better aboveground biomass data values than the more physically-based models or the global equations, probably because of a lack of in situ measurements of the wood specific gravity. Mean plot aboveground biomass figures of 30, 41, and 35 Mg ha-1 were recorded for 57, 217, and 166 plots, respectively, systematically distributed across the tropical dry forests of Durango, and Sinaloa, Mexico. This source of information is fundamental for the development of conventional and sustainable management plans of Mexico's tropical dry forest ecosystems.
Literature cited
Brandeis, T.J., M. Delaney, B.R. Parresol, and L. Royer. 2006. Development of equations for predicting Puerto Rican subtropical dry forest biomass and volume. Forest Ecol. Manag. 233, 133-142. Doi: 10.1016/j.foreco.2006.06.012 [ Links ]
Brown, S. 1997. Estimating biomass and biomass change of tropical forests. FAO Forestry Paper No. 134. FAO, Rome. [ Links ]
Brown, S., A.J.R. Gillespie, and A.E. Lugo. 1989. Biomass estimation methods for tropical forests with applications to forest inventory data. Forest Sci. 35, 881-902. [ Links ]
Cairns, M.A., S. Brown, E.H. Helmer, and G.A. Baumgardner. 1997. Root biomass allocation in the world' s upland forests. Oecologia 111, 1-11. Doi: 10.1007/s004420050201 [ Links ]
Cairns, M.A., P.K. Haggerty, R. Alvarez, B.H.J. De Jong, and I. Olmsted. 2000. Tropical Mexico's recent land-use change: a region's contribution to the global carbon cycle. Ecol. Appl. 10, 1426-1441. Oi: 10.1890/1051-0761(2000)010[1426:TMSRLU]2.0.CO;2 [ Links ]
Cairns, M.A., I. Olmsted, J. Granados, and J. Argaez. 2003. Composition and aboveground tree biomass of a dry semi-evergreen forest on Mexico's Yucatan Peninsula. Forest Ecol. Manag. 186, 125-132. Doi: 10.1016/S0378-1127(03)00229-9 [ Links ]
Canadell, J.G. and M.R. Raupach. 2008. Managing forests for climate change mitigation. Science 320, 1456-1457. Doi: 10.1126/science.1155458 [ Links ]
Chave, J., C. Andalo, S. Brown, M.A. Cairns, J.Q. Chambers, D. Eamus, H. Fölster, F. Fromard, N. Higuchi, T. Kira, J.-P. Lescure, B.W. Nelson, H. Ogawa, H. Puig, B. Riéra, and T. Yamakura. 2005. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 145, 87-99. Doi: 10.1007/s00442-005-0100-x [ Links ]
Chave, J., H.C. Muller-Landau, T.R. Baker, T.A. Easdale, H.T. Steege and C.O. Webb. 2006. Regional and phylogenetic variation of wood density across 2456 neotropical tree species. Ecol. Appl. 16, 2356-2367. [ Links ]
Gómez-Díaz, J.D., J.D. Etchevers, A.I. Monterroso, K. Paustian, C. Hidalgo, J.A. Tinoco-Rueda, and E. Guizar. 2011. Above and belowground biomass and carbon stocks of a tropical dry forest of Central Mexico. Journal of Tropical Ecology. Submitted.
Houghton, RA. 2005. Aboveground forest biomass and the global carbon balance. Global Change Biol. 11, 945-958. Doi: 10.1111/j.1365-2486.2005.00955.x [ Links ]
Jenkins, J.C., D.C. Chojnacky, L.S. Heath, and R.A. Birdsey. 2003. National-scale biomass estimators for United States trees species. Forest Sci. 49, 12-35. [ Links ]
Ketterings, Q.M., R. Coe, M. Van Noordwijk, Y. Ambagau, and C.A. Palm. 2001. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. Forest Ecol. Manag. 146, 199-209. Doi: 10.1016/S0378-1127(00)00460-6 [ Links ]
Martínez-Yrizar, A., J.M. Maass, L.A. Pérez-Jiménez, and J. Sarukhán. 1996. Net primary productivity of a tropical deciduous forest ecosystem in western Mexico. J. Trop. Ecol. 12, 169-175. Doi: 10.1017/S026646740000938X [ Links ]
McKendry, P. 2002. Energy production from biomass (part 1): overview of biomass. Bioresour. Technol. 83, 37-46. Doi: 10.1016/S0960-8524(01)00118-3 [ Links ]
Mokany, K., R.J. Raison, and S.A. Prokushkin. 2006. Critical analysis of root:shoot ratios in terrestrial biomes. Global Change Biol. 12, 84-96. Doi: 10.1111/j.1365-2486.2005.001043.x [ Links ]
Montagu, K.D., K. Düttmer, C.V.M. Barton, and A.L. Cowei. 2005. Developing general allometric relationships for regional estimates of carbon sequestration-an example using Eucalyptus pilularis from seven contrasting sites. Forest Ecol. Manag. 204, 115-129. Doi: 10.1016/j.foreco.2004.09.003 [ Links ]
Návar, J. 2009a. Biomass component equations for Latin American species and groups of species. Ann. Forest Sci. 66, 208. Doi: 10.1051/forest/2009001 [ Links ]
Návar C., J.J. 2009b. Allometric equations and expansion factors for tropical dry trees of eastern Sinaloa, Mexico. Trop. Subtrop. Agroecosyst. 10, 45-52. [ Links ]
Návar, J. 2010. Measurement and assessment methods of forest aboveground biomass: a literature review and the challenges ahead. pp. 27-64. In: Momba, M. and F. Bux (eds.). Biomass. InTech, Rijeka, Croatia. [ Links ]
Palacio-Prieto, J.L., G. Bocco, A. Velázquez, J.F. Mas, F. Takaki- Takaki, A. Victoria, L. Luna-González, G. Gómez-Rodríguez, J. López-García, M. Palma M., I. Trejo-Vázquez, A. Peralta H., J. Prado-Molina, A. Rodríguez-Aguilar, R. Mayorga-Saucedo, and F. González M. 2000. La condición actual de los recursos forestales en México: resultados del Inventario Forestal Nacional 2000. Invest. Geográf. 43, 183-200. [ Links ]
Parolin, P. 2002. Radial gradients in wood specific gravity in trees of Central Amazonian floodplains. IAWA J. 23, 449-457. Doi: 10.1163/22941932-90000314 [ Links ]
Ter-Mikaelian, M.T. and M.D. Korzukhin. 1997. Biomass equations for sixty-five North American tree species. Forest Ecol. Manag. 97, 1-24. Doi: 10.1016/S0378-1127(97)00019-4 [ Links ]
West, G.B., J.H. Brown, and B.J. Enquist. 1999. A general model for the structure and allometry of plant vascular systems. Nature 400, 664-667. Doi: 10.1038/23251 [ Links ]
Williams, R.J., A. Zerihum, K.D. Montagu, M. Hoffman, L.B. Hutley, and X. Chen. 2005. Allometry for estimating aboveground tree biomass in tropical and subtropical eucalypt woodlands: towards general predictive equations. Aust. J. Bot. 53, 607-619. Doi: 10.1071/BT04149 [ Links ]
Xiang, W., S. Liu, X. Deng, A. Shen, X. Lei, D. Tian, M. Zhao, and C. Peng. 2011. General allometric equations and biomass allocation of Pinus massoniana trees on a regional scale in southern China. Ecol. Res. 26, 697-711. Doi: 10.1007/s11284-011-0829-0 [ Links ]
Youkhana, A.H. and T.W. Idol. 2011. Allometric models for predicting above- and belowground biomass of Leucaena-KX2 in a shaded coffee agroecosystem in Hawaii. Agroforest. Syst. 83, 331-345. Doi: 10.1007/s10457-011-9403-6 [ Links ]













