Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Agronomía Colombiana
versão impressa ISSN 0120-9965
Agron. colomb. vol.32 no.3 Bogotá set./dez. 2014
https://doi.org/10.15446/agron.colomb.v32n3.46086
Doi: 10.15446/agron.colomb.v32n3.46086
1 Department of Agronomy, Faculty Agricultural Sciences, Universidad Nacional de Colombia. Bogota (Colombia). aqedarghanco@unal.edu.co
2 Institute for Applied Statistics and Computers, Universidad de Los Andes. Merida (Venezuela).
3 Deparament of Mathematics, Faculty of Science, Universidad de Pamplona. Pamplona (Colombia).
Received for publication: 9 October, 2014. Accepted for publication: 27 November, 2014.
Abstract
In some agricultural research, a treatment applied to an experimental unit may affect the response in the neighboring experimental units. This phenomenon is known as overlap. In this article, a test to evaluate this effect in the Draper and Guttman model was developed by imposing side conditions on the parameters of a two-way classification model to obtain a re-parameterized model which can be used in different neighboring patterns of experimental units, usually plants within a crop, whenever the nearest neighbor is considered a directly affected experimental unit and the two-way model is used. Three methods, namely maximum likelihood, least squares with side conditions and generalized inverse, were used to estimate the parameters of the original model in order to calculate the value of the test statistics for the null hypothesis associated with the absence of the overlapping effect. The three alternatives were invariant with respect to the use of test. The proposed test is simple to adopt and can be implemented in agronomy since its asymptotic nature is in agreement with the large number of experimental units which generally exist in this type of research, where each plant represents the experimental unit being assessed.
Key words: perpendicular projection operator, side conditions, experimental design.
Resumen
En algunas investigaciones agrícolas, un tratamiento aplicado sobre una unidad experimental puede afectar la respuesta de unidades experimentales vecinas. Este fenómeno es conocido como solapamiento. En este artículo se desarrolló un test para evaluar este efecto, sobre el modelo de Draper y Guttman, mediante la imposición de condiciones laterales sobre los parámetros del modelo de clasificación de dos vías para obtener un modelo reparametrizado, el cual puede usarse bajo diferentes patrones de vecindad de las unidades experimentales, usualmente plantas dentro de un cultivo, siempre y cuando sea considerado el vecino más cercano como la unidad experimental directamente afectada y el modelo sea de dos vías. Fueron usados tres métodos para estimar los parámetros del modelo original, a saber, el método de máxima verosimilitud, el método de mínimos cuadrados con imposición de condiciones laterales y el uso de una inversa generalizada para calcular el valor del estadístico de prueba para la hipótesis nula asociada a la ausencia del efecto de solapamiento. Las tres alternativas resultaron invariantes con respecto al uso del test. La prueba propuesta es sencilla de adoptar y se puede implementar en el campo de la agronomía, ya que su naturaleza asintótica está de acuerdo con el gran número de unidades experimentales que generalmente existen en este tipo de investigaciones, donde cada planta representa la unidad experimental evaluada.
Palabras clave: operador de proyección perpendicular, condiciones laterales, diseño experimental.
Introduction
In some agricultural tests, a treatment that is applied to an experimental unit may affect the response in the neighboring experimental units. This phenomenon is known as overlap. For example, in variety testing, the effect of a neighbor can be attributed to differences in height between plants, strength of roots, and date of germination, among others. Hide and Read (1990) discussed this situation in potato cultivation. The treatments applied to crops for fertilization plans, irrigation and pesticide applications can be dispersed to other plots or adjacent experimental units, which can affect the response in the neighboring units. An example of this situation for an irrigation experiment can be found with Bhalli et al. (1964). This overlapping phenomenon has been modeled by several researches; for example, Pearce (1957) considered a model in which each treatment had a direct influence on the plot in which they were applied and an overlap effect on the neighboring plots. Draper and Guttman (1980) also considered such a model, discussing some approximate testing methods as well as a confidence interval for the overlap effect. Draper and Guttman (1980) used a nonlinear model in which the overlapping was attributed to all the effects considered in the model. Such a model is written as:
Y = Xb + aWXb + e (1)
where the random vector Y denotes the response of n experimental units, X is a known design matrix of dimension n × p with rank q< p, b is a p-dimensional vector of unknown parameters consisting of the effects of blocks and treatments, a is the overlapping coefficient, and W = (wij) is a matrix of known weights of dimension n × n, where wij denotes the effect of unit j on unit i; such that Snj=1 wij = 1 for all i; and wij = 0, wij ≥ 0 for all i and j. The fact that the X matrix is of an incomplete rank generates the possibility of imposing side conditions on the parameters so that an estimator for the b vector can be obtained. Finally, it is assumed that the distribution of the error vector e is normal and independent with an expected value of zero (E(e) = 0) and variance of s2I, where I is an identity matrix. Shukla and Subrahmanyan (1999) considered a generalization of the first model represented by (1), which only included a subset of all the direct effects influencing the neighboring plots. In the following sections of the article, some important results which allowed the construction of Rao's score test for a of model (1) are presented; in the methods section, we explain the side condition technique, the obtainment of several matrices associated with the model of Draper and Guttman (1980) and, finally, we present Rao's score test under the imposition of side conditions.
Methods
Side conditions and associated matrices in the Draper and Guttman model
The technique to impose side conditions is very well-known in the area of experimental design since it provides the necessary (linear) restrictions which can assure that the estimation of the parameters is unique. Another use of side conditions is the imposition of arbitrary restrictions on the estimators so that the normal equations can be simplified. In this case, the estimators have exactly the same behavior when a generalized inverse of XTX is used to obtain the vector of parameters. Let q be the rank of the design matrix X where q<p<n in (1), then XTXb represents a set of p estimable functions of b. The side conditions must be non-estimable functions of b. Since the rank of X is q and, hence, the deficiency of this rank is p-q; conditions such as Lb = 0 or L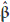 = 0 to obtain a unique solution for
= 0 to obtain a unique solution for 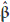 should be defined where L is a matrix of dimension (p-q)× p with a rank of L being p-q such that Lb is a set of non-estimable functions. The (1) model under the null hypothesis a = a0 along with the side conditions is written as:
should be defined where L is a matrix of dimension (p-q)× p with a rank of L being p-q such that Lb is a set of non-estimable functions. The (1) model under the null hypothesis a = a0 along with the side conditions is written as:
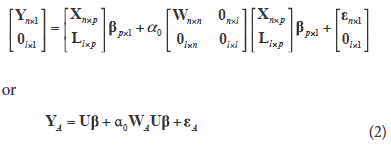
Where UT = [XT LT] has rank p, WA is a matrix of weights with l additional rows, and where l represents the number of imposed linear restrictions. The UTU matrix is of a p × p dimension and rank p, which generate the system of normal equations UTU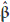 = UTYA, where YA is the vector of responses expanded with zeros and has a unique solution for
= UTYA, where YA is the vector of responses expanded with zeros and has a unique solution for 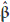 (Graybill, 1976). In order to illustrate the above described procedure, let us suppose that we have a two-way classification model (treatments and blocks) which will be written as Yij = m + ti + dj + eij; (i = 1, 2,â¦, t > 1); (j = 1, 2,â¦, b > 1) with ti as the effect of the ith treatment and dj as the effect of the jth block, which in matrix form is written as Y = Xb + e. In this model, there is a deficiency in rank p-q = 2, with p = t + b + 1 and q = t + b-1. In order to solve this problem of rank deficiency in this design model, the usual non-estimable functions Sti=1 ti = 0 and Sbj=1 dj = 0 can be used, which can be expressed in the matrix form as the following set of non-estimable functions:
(Graybill, 1976). In order to illustrate the above described procedure, let us suppose that we have a two-way classification model (treatments and blocks) which will be written as Yij = m + ti + dj + eij; (i = 1, 2,â¦, t > 1); (j = 1, 2,â¦, b > 1) with ti as the effect of the ith treatment and dj as the effect of the jth block, which in matrix form is written as Y = Xb + e. In this model, there is a deficiency in rank p-q = 2, with p = t + b + 1 and q = t + b-1. In order to solve this problem of rank deficiency in this design model, the usual non-estimable functions Sti=1 ti = 0 and Sbj=1 dj = 0 can be used, which can be expressed in the matrix form as the following set of non-estimable functions:
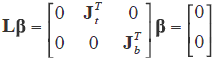
denoting Jt and Jb as the vectors of ones of the t and b elements, respectively. The matrices UTU,(UTU)-1,(UTU)-1XT and X(UTU)-1 XT are needed in the estimation of the vector of parameters b,error variance and, therefore, for obtaining Rao's score test for overlapping. However, here, we only present the final expression (Darghan, 2010); it is the comprehensive development of related matrix calculations), namely:
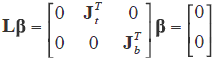
with n=bt, X =(J Xt Xd), where Xt and Xd are the sub-matrices of the design matrix associated with the effects of the treatments and blocks respectively, Mt = b-1XtXTt , Md = t-1XdXTd and MJ= n-1JJT, which are all perpendicular projection matrices onto the column spaces of Xt, Xd and J, respectively, denoted with C(Xt), C(Xd) and C(J). This last statement is shown in a later theorem. The space spanned by the columns of a vector or matrix called a column space is written as C( ), placing in the brackets the vector or matrix of interest. Another interesting use of side conditions for obtaining the re-parameterization of a model can be described as follows: Let Lb = 0 define the side conditions in the model (1). If Lb = 0 holds, then b belongs to the orthogonal (⊥) complement of C(LT), namely b∈C(LT)⊥. Let Z be such that C(LT) = C(Z), then b = Zg for some g; then, by substituting b with Zg and defining X0 = XZ in model (1), we get

Besides, if Lb is not estimable, then C(X) = C(X0) and the third model represented by (4) is a re-parameterization of model (1) (Christensen, 2011).
Rao's score test
This section summarizes the theory of likelihood for the score test. Further information about score tests can be found in (Rao, 1973) and (Cox and Hinkley, 2000). The article published by (Rao, 1948) introduced the fundamental principle of a test based on the score function as an alternative method to the likelihood ratio test and to Wald's method. Several authors have described the attractive properties of the method; among them, Chandra and Joshi (1985), Bera and Mckenzie (1986) and Bera and Bilias (2001). For a better understanding of the test, we introduce its notation, which is maintained until the development of the test for a. Suppose there are n independent observations Y1,â¦, Yn identically distributed with a density function of f(y;q) that satisfies the conditions of a regularity given by (Rao, 1973), where q is a vector of parameters of dimension p × 1, with q∈Q⊂R p. The log-likelihood function, the score function and the expected information matrix are defined respectively as l(q) = log(Pni=1 f(yi;q)), s(q) = ∂l(q)/∂q, F(q) = – E(∂2l(q)/∂q∂qT).
The hypothesis to test is H0 : h(q) = c, where h(q) is a r-dimensional vector function of q with r ≤ p and c is a vector of known constants. In addition, it is assumed that H(q) = ∂h(q)/∂q is a full column rank matrix. In the one-dimensional case of c, when p =1 with H0 : q = q0 and using the Neyman-Pearson lemma, (Rao and Poty, 1946) proved that the most powerful local test for H0 is ks(q0)>l, where l is determined such that the size of the test is equal to a pre-assigned value of the significance level, with k as +1 or -1, respectively for alternatives q > q0 or q < q0 (Wald, 1941), and as the result of which under H0, s(q0) has asymptotically normal distribution with a mean of zero and a variance of F(q). This result led (Rao, 1948) to suggest a test based on s2(q0)/F(q)-1 as a c12 variable when n is large. The generalization of the test when p ≥ 2 was developed by (Rao, 1948), which led him to the statistical test based on s(q0)TF(q)-1 s(q0), which has a c2g distribution with g degrees of freedom.
Results
Here, the results obtained by applying Rao's test score to the overlap model are presented as well as some theorems generated as a result of the partition of the design matrix to solve the problem of incomplete rank in the estimation process and the statistic test to evaluate the effect of overlapping.
Suppose we want to test the hypothesis H0 : a = 0 against H0 : a ≠ 0 in model (1), under H0, this model is the usual linear model Y = Xb + e; however, X is not of a full column rank; in this sense, the p parameters in b are not unique. We then ascertained whether b could be estimated. Using least-squares in (1), we obtained the normal equations XTX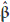 = XTY. However, since X was not of a full column rank, XTX had no inverse; as a consequence, the normal equations did not have a unique solution, despite the fact that this system was consistent if and only if XTX(XTX)- XTY = XTY, where (XTX)- is a generalized inverse of XTX. Since the normal equations were consistent, a solution is:
= XTY. However, since X was not of a full column rank, XTX had no inverse; as a consequence, the normal equations did not have a unique solution, despite the fact that this system was consistent if and only if XTX(XTX)- XTY = XTY, where (XTX)- is a generalized inverse of XTX. Since the normal equations were consistent, a solution is:

For a particular generalized inverse (XTX)-, the expected value of 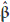 in (1) under H0 is E(
in (1) under H0 is E(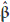 ) = (XTX)- XTYb, thus
) = (XTX)- XTYb, thus 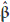 is not an unbiased estimator of b; furthermore, the expression (XTX)- XTYb is not invariant to the choice of (XTX)-, thus,
is not an unbiased estimator of b; furthermore, the expression (XTX)- XTYb is not invariant to the choice of (XTX)-, thus, 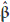 in (5) does not estimate b. With respect to the estimation of s2, in model (1), we define:
in (5) does not estimate b. With respect to the estimation of s2, in model (1), we define:
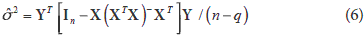
where n is the number of rows of X which has rank q. The estimator in (6) is unbiased for s2 and invariant to the choice of 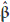 and to the choice of generalized inverse (XTX)-. For the non-full column rank model (1), under H0, we now assume that e is distributed as Nn (0;s2I). With the normality assumption we can obtain a maximum likelihood estimator for (1) under H0. In this case, we have the same estimator for b which is given by the least square estimation but a biased estimator for s2 is obtained, which can be written as
and to the choice of generalized inverse (XTX)-. For the non-full column rank model (1), under H0, we now assume that e is distributed as Nn (0;s2I). With the normality assumption we can obtain a maximum likelihood estimator for (1) under H0. In this case, we have the same estimator for b which is given by the least square estimation but a biased estimator for s2 is obtained, which can be written as 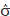 2 = [n-1YTIn - X(XTX)- XT]Y. The lack of uniqueness in the estimate for b using two different estimation methods in (1) leads us to the use of (2). In this model, the problem of the rank of X is solved with the imposition of side conditions to proceed with the estimation of the parameters using least squares. Using model (2) restricted by H0 we obtain
2 = [n-1YTIn - X(XTX)- XT]Y. The lack of uniqueness in the estimate for b using two different estimation methods in (1) leads us to the use of (2). In this model, the problem of the rank of X is solved with the imposition of side conditions to proceed with the estimation of the parameters using least squares. Using model (2) restricted by H0 we obtain 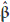 = (UTU)-1 UTYA = (UTU)-1 UTY and
= (UTU)-1 UTYA = (UTU)-1 UTY and 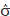 2 = YT[In - X(UTU)- XT]Y/(n-q), which are unique and unbiased. Also the error vector has two interesting features: it has singular normal distribution and, therefore, the log-likelihood function doesn't exist and contains the matrix given in (3), which is very important in the development of the theorems presented below and can be extended in the balanced two-way classification model with more than one observation per cell by just modifying the design and weight matrices in order to adjust for the replications of each treatment.
2 = YT[In - X(UTU)- XT]Y/(n-q), which are unique and unbiased. Also the error vector has two interesting features: it has singular normal distribution and, therefore, the log-likelihood function doesn't exist and contains the matrix given in (3), which is very important in the development of the theorems presented below and can be extended in the balanced two-way classification model with more than one observation per cell by just modifying the design and weight matrices in order to adjust for the replications of each treatment.
Theorem 1. Let Mt = b-1XtXTt, Md = t-1XdXTd and MJ = n-1JJT be perpendicular projection matrices onto the respective column spaces of Xt, Xd and J, such that C(Mt) = C(Xt), C(Md) = C(Xd) and C(MJ) =C(J).
Proof. An inspection of the matrices Mt, Md and MJ allows for a verification of the symmetry and idempotent properties, which is enough to prove that these matrices are all perpendicular projection matrices onto the respective column spaces of Xt, Xd and J. To prove that C(Mt) = C(Xt), we can refer to the B.51 proposition in (Christensen, 2011). In the cases where C(Md) = C(Xd) and C(MJ) = C(J), the same procedure can be followed.
Theorem 2. For matrices Mt, Md and MJ, it holds that if MtMd = MJ, MtMJ =MJ and MdMJ = MJ, then C(I - X(UTU)- XT) = C(I - 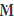 ) ⊂ C(MJ)⊥.
) ⊂ C(MJ)⊥.
Proof. The proof is obvious by the very definition of the matrices Mt, Md and MJ in the two-way classification design without interaction. To prove that C(I - 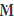 ) ⊂ C(MJ)⊥, it is sufficient to multiply I -
) ⊂ C(MJ)⊥, it is sufficient to multiply I - 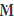 with MJ and observe that their product is zero. In addition, the rank of C(MJ)⊥ as n-1 is greater than the rank of C(I -
with MJ and observe that their product is zero. In addition, the rank of C(MJ)⊥ as n-1 is greater than the rank of C(I - 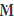 ), whose value is n - q, whenever q > 1 in the two-way classification model without interaction.
), whose value is n - q, whenever q > 1 in the two-way classification model without interaction.
Theorem 3. 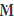 is the perpendicular projection matrix on C(X), where
is the perpendicular projection matrix on C(X), where 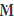 = X(UTU)-1XT.
= X(UTU)-1XT.
Proof. In order to prove that 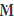 is the perpendicular projection matrix on C(X), it is necessary to verify that
is the perpendicular projection matrix on C(X), it is necessary to verify that 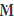 is symmetric and idempotent. The symmetry obviously results from equation (3) when verifying that
is symmetric and idempotent. The symmetry obviously results from equation (3) when verifying that 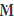 =
= 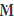 T. So we only have to prove idempotence (
T. So we only have to prove idempotence (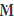 =
= 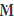 2). Since
2). Since 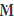 = Mt + Md - MJ, therefore
= Mt + Md - MJ, therefore 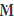 2 = (Mt + Md - MJ)2, and using the previous theorems, we have
2 = (Mt + Md - MJ)2, and using the previous theorems, we have 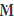 =
=  2.
2.
Theorem 4. The matrix (UTU)-1 = (XTX + LTL)-1 is a g-inverse of XTX.
Proof. A generalized inverse of XTX is any G matrix such that XTXGXTxX = XTX. Let G = (XTX + LTL)-1, then XTXGXTX = XTX(XTX + LTL)-1, but replacing  with theorem 3, we have XTXGXTX = XT
with theorem 3, we have XTXGXTX = XT X and as
X and as  X = X for the same theorem, we have XTXGXTX = XTX.
X = X for the same theorem, we have XTXGXTX = XTX.
Theorem 5. The matrices Ma = Mt - MJ and Mh = Md - MJ are perpendicular projection operators; additionally, C(Ma) ⊥ C(Mh), C(Ma) ⊥ C(Md) and C(Mh) ⊥ C(Mt).
Proof. To start, we will prove that Ma and Mh are idempotent matrices, which we obtain by verifying that (Mt - MJ)2 = M2t + M2J - MtMJ - MJMt = Mt - MJ. The symmetry of Mt - MJ obviously results when we substitute Mt with b-1Xt XTt and MJ with n-1JJT, from which we obtain MTa = Ma. The same procedure may be used in the case of Mh. In order to prove that C(Ma) ⊥ C(Mh) or, in other words, to prove that C(Ma) is contained in the orthogonal complement of C(Mh), it should be sufficient to verify that the product of the matrices associated with these spaces is null. In the first case, we have(Mt - MJ) (Md - MJ) = MtMd - MtMJ - MJMd + M2J = 0; for the cases C(Ma) ⊥ C(Md) and C(Mh) ⊥ C(Mt) the same procedure is followed.
To develop Rao's score test for overlapping, we need the expected information matrix which is constructed from the log-likelihood function. In the (1) model, the log-likelihood is singular due to the deficiency in the rank of X. Thus, models (1) and (2) are not used in the construction of the test, but we still use their estimates for b and s2. The log-likelihood function for (4) is:
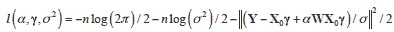
from which, under H0, we obtain: 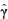 = (XT0X0)-1 XT0Y and
= (XT0X0)-1 XT0Y and 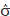 2 = n-1YT[In - M0]Y as the perpendicular projection matrix on C(X0). The score vector is:
2 = n-1YT[In - M0]Y as the perpendicular projection matrix on C(X0). The score vector is:
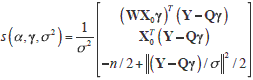
with Q = (In + aW)X0. If we denote sa (a,g,s2) the component of the score vector corresponding to the parameter of interest (a), the score statistic to test H0 : a = 0 is:
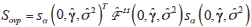
where 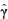 and
and 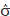 2 are the maximum likelihood estimators of g, s2 in (4) and
2 are the maximum likelihood estimators of g, s2 in (4) and 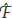 1 (0,
1 (0,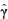 ,
,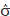 2) is the component in the expected information matrix evaluated at a = 0. The expected information inverse matrix is:
2) is the component in the expected information matrix evaluated at a = 0. The expected information inverse matrix is:
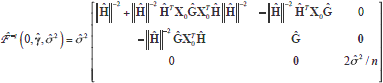
where 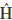 = WX0g and
= WX0g and 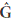 = (XT0(In -
= (XT0(In - 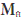 )X0)-1, with
)X0)-1, with 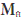 =
= 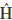 ||
||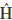 ||-2
||-2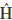 T (
T (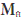 as the perpendicular projection operator on C(
as the perpendicular projection operator on C(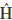 )). Now, when evaluating sa (a,g,s2) in sa (0,
)). Now, when evaluating sa (a,g,s2) in sa (0,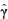 ,
,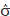 2) and grouping terms, we obtain:
2) and grouping terms, we obtain:
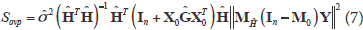
The score statistic test for overlap has a c2 distribution with a g = 1 degree of freedom, which tests a in the Draper and Guttman model. The statistic in (7) depends on 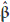 only through
only through 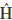 (and hence
(and hence 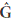 ). The estimates for b and s2 in models (1) and (4) can be substituted in (7), verifying that the same value of the statistic is obtained. Such a result is not surprising given that models (1) and (4) have the same estimation space C(X). Darghan (2010) showed the invariance property of Sovp using (XTX + LTL)-1 or (XTX)-.
). The estimates for b and s2 in models (1) and (4) can be substituted in (7), verifying that the same value of the statistic is obtained. Such a result is not surprising given that models (1) and (4) have the same estimation space C(X). Darghan (2010) showed the invariance property of Sovp using (XTX + LTL)-1 or (XTX)-.
Discussion
A statistical test based on Rao's score test has been developed for the overlapping effect in a re-parameterization of the Draper and Guttman model (Draper and Guttman, 1980). Although the phenomenon of overlap is not new in agricultural sciences, evaluation by means of a model is relatively new. Few authors have modeled this phenomenon. In 1999, Shukla and Subrahmanyam (1999) proposed an exact test and confidence intervals to assess the overlap coefficient using the model of Draper and Gutman, but using the Likelihood ratio rest. Despite the side conditions imposed in the original model to resolve the no-full-rank restriction in the design matrix and obtain unique and unbiased estimated parameters in (2), the error vector introduced the singular normal distribution; so, in this case, it is not defined as a log-likelihood function and, hence, it was impossible to obtain the estimators by maximum likelihood as it was not possible to apply the methodology of Rao to build the hypothesis testing. So far, we can say that the original model and the extended model by side conditions presented the respective restrictions of not being able to obtain the inverse of the expected Fisher information matrix or singular normal distribution. Thus, the test was developed by re-parameterization of the original model. The natural maximum likelihood estimators were obtained for the parameters g and s2 under H0 and, with these same estimators, the score test for overlapping was evaluated. The dependence of the statistical test on the parameters allows for replacing the two sets of estimators obtained by least square estimation: one for b and another for s2 in each studied model. The statistical test was invariant, which was expected because models (1) and (4) were equivalent and model (2) provided an estimate for b, belonging to the same estimation space of models 1 and 4. The statistical test for overlapping should be of wide application in agronomical research and has extensive practical value because the application of a variance analysis on a data set that was collected in the field has experienced the effect of overlap, generating spurious results as the effect of the treatments is confused since the same experimental unit could be receiving more than one treatment at a time. This test is easy to adopt as long as the layout of the used experimental design involves a model similar to that of Draper and Guttman whenever the nearest neighbor is considered a possible source of overlapping. Although the used example involved a test of overlapping by means of only the effects included in the two-way model, it can also be tested for any number of factors and their interactions as well as for a subgroup of effects and not only the use of the nearest neighbor by just modifying the design matrix and the matrix of the weights in the re-parameterized model. Statistics have been tested in various agricultural applications (Darghan et al., 2012) as well as in the area of education (Darghan et al., 2014) not only in design models, but also in the context of response surface modeling (Darghan et al., 2011), obtaining similar results as observed in the field (Darghan, 2010).
Conclusions and recommendations
The developed overlap test can be used in the field of agronomy where it is increasingly suspected that applied treatments can move from one experimental unit to that of the nearest neighbor and that the presence of overlap may invalidate the comparison of treatments when using the analysis of variance associated with a linear model, in this case, a two-way classification model. The asymptotic nature of the test requires a large amount of experimental units for it to be valid. The results obtained in applications using linear models have been similar to those observed in field results. Once the overlap coefficient has been estimated, the analysis of variance can be corrected by the overlap effect. Monte Carlo simulation studies as well as agricultural applications in the field of information technology and communication will complement the properties of the test, which can be extended to more complex experimental designs using neighboring patterns that cover all of the experimental units that are being studied.
Literature cited
Bera, A.K. and Y. Bilias. 2001. Rao's score, Neyman's C(a) and Silvey's LM tests: an essay on historical developments and some new results. J. Stat. Plan. Infer. 97, 9-44. Doi: 10.1016/S0378-3758(00)00343-8 [ Links ]
Bera, A.K. and C.R. Mckenzie. 1986. Alternative forms and properties of thescore test. J. Appl. Stat. 13, 13-25. Doi: 10.1080/02664768600000002 [ Links ]
Bhalli, M.A., A.D. Day, H. Tucker, R.K. Thompson, and G.D. Massey. 1964. Endborder effects in irrigated barley yield trials. J. Appl. Stat. 56, 346-348. doi: 10.2134/agronj1964.00021962005600030028x [ Links ]
Chandra, T.K. and S.N. Joshi. 1985. Comparison of the likelihood ratio, Rao's and Wald's tests and a conjecture of C.R. Rao. Shankhyã: the Indian J. Stat. Ser. A 45, 226-246. [ Links ]
Christensen, R. 2011. Plane answers to complex questions. the theory of linear models. 4th ed. Springer-Verlag, New York, NY. [ Links ]
Cox, D.R. and D.V. Hinkley. 2000. Theoretical statistics. Chapman and Hall; CRC, London. [ Links ]
Darghan, A.E. 2010. Test score de Rao para el modelo de solapamiento de Draper y Guttman. PhD thesis. Faculty of Sciences, Universidad de los Andes, Merida, Venezuela. [ Links ]
Darghan, A.E., P. Sinha, and A. Goitia. 2011. Score test para el coeficiente de solapamiento en modelos de superficies de respuesta de primer y segundo orden. Dyna 165, 234-245. [ Links ]
Darghan C., A.E. P. Sinha S., and A. Goitia A. 2012. Una aplicación del test de solapamiento en un modelo de clasificación de dos vías reparametrizado. Rev. F. Agron. (LUZ) 29, 124-137. [ Links ]
Darghan, A.E., C. Monroy, and G. Montañez. 2014. Evaluación del solapamiento de información en las investigaciones que comparan modalidades de enseñanza asociados a las tecnologías de información y comunicación. Bistua: Rev. Fac. Cienc. Básicas 12, 3-15. [ Links ]
Draper, N.R. and I. Guttman. 1980. Incorporating overlap effects from neighbouring units into response surface models. Appl. Statist. 29, 128-134. [ Links ]
Graybill, F.A. 1976. Theory and application of the linear model. Duxbury Press, North Scituate, MA. [ Links ]
Hide, G.A. and P.J. Read. 1990. Effect of neighbouring plants on the yield of potatoes from seed tubers affected with gangrene (Phoma foveata) or from plants affected with stem canker (Rhizoctonia solani). Ann. Appl. Biol. 116, 233-243. Doi: 10.1111/j.1744-7348.1990.tb06603.x [ Links ]
Pearce, S.C. 1957. Experimenting with organisms as blocks. Biometrika 44, 141-149. [ Links ]
Rao, C.R. 1948. Large sample tests of statistical hypothesis concerning several parameters with applications to problems of estimation. Math. Proc. Camb. Phil. Soc. 44, 50-57. Doi: 10.1017/S0305004100023987 [ Links ]
Rao, C.R. 1973. Linear statistical inference and its applications. 2nd ed. Wiley, New York, NY. Doi: 10.1002/9780470316436 [ Links ]
Rao, C.R. and S.J. Poty. 1946. On locally most powerful tests when alternative are one sided. Shankhya 7, 439. [ Links ]
Shukla, G.K. and G.S.V. Subrahmanyan. 1999. A note on a test and confidence interval for competition and overlap effects. Biometrics 55, 273-276. Doi: 10.1111/j.0006-341X.1999.00273.x [ Links ]
Wald, A. 1941. Some examples of asymptotically most powerful tests. Ann. Math. Statist. 12, 396-408. Doi: 10.1214/aoms/1177731678 [ Links ]













