Introduction
The leaf angle distribution plays a crucial role in processes such as photosynthesis (Campbell, 1990), biomass production and energy balance (Mooney et al., 1977), the intra-canopy and inter-canopy microclimate (Thanisawan-yangkura et al., 1997) and even light competition (Hikosaka and Hirose, 1997). These distributions also determine the radiation reflected by the canopy, which affects the spectral signature observed by remote sensing satellites (Smith, 1982; Verhoef and Bach, 2007; Knyazikhin et al, 2013). The leaf orientation is given by the direction of the inclination angles and azimuthal angles of the leaf (Sinoquet and Andrieu, 1993; Jaramillo et al., 2006). In most canopies, the leaves distribution can be characterized by the distribution of the leaf angle frequencies, when this approaches to an azimuthal symmetry (de Wit, 1965; Ross, 1975; Goudriaan, 1988; Goudriaan and Monteith, 1990).
The planophile, erectophile, plagiophile and extremophile distributions describe classical trends in the orientation of the leaves according to de Wit (1965). When insufficient information is available on the canopy distribution, it can be assumed that its distribution is spherical (area elements are all inclined as a sphere) (Goudriaan, 1988). Campbell (1990) generalized the spherical distribution by introducing the ellipsoidal inclination function in which the values of x are within the range of 0.1 (vertical distribution) to 10 (vertical distribution); the spherical distribution has a value x of 1.0 (Campbell and Norman, 1988; Wang and Jarvis, 1988).
The above-mentioned functions are estimated by a single parameter; however, the Beta distribution is estimated with two parameters, which provide a better performance when the canopy has various fractions of leaf area with various leaf angles (Wang et al, 2007). Goel and Strebel (1984) suggested that the Beta function with two parameters (v and µ) could be considered as a candidate for the distribution of "universal" leaf angles, which are applicable in most canopies. The leaf angle distribution may be affected by water shortages and heat (Sinoquet and Andrieu, 1993). The age of the plant and its size are also factors that affect the structural characteristics of the leaf, stem and canopy profiles (Niinemets, 2010). Leaf angle distribution function is useful to describe flux of solar radiation per unit leaf area by means of canopy in models of radiation distribution, because the light interception depends directly of the leaf orientation (Falster and Westoby, 2003; Flerchinger and Yu, 2007).
The aim of this study was to find the leaf angle distribution function that best describes the distribution of angles present in C. arabica L. variety Castillo® in the three profiles of the tree and their combination.
Materials and methods
Location
The study was conducted during the month of August, 2014, at the Central Station Naranjal of Cenicafé in Chinchina (Colombia), located at 04°58' N y 75°39' W, with an altitude of 1,381 m, an annual average rainfall of2,795 mm, an annual average temperature of 20.9°C and a relative humidity of 76.9%.
Sampling method
The leaf angles were recorded in 1,559 leaves located in the upper, middle and lower profiles of the canopy. For each profile, the total number of orthotropic nodes of the stem per tree was divided into three equal parts. Leaves sampled in the field came from 15 coffee trees of the Castillo® variety (Coffea arabica L.) that were 2.6 years of age and seeded at a density of 5,000 plants/ha (2x1 m between rows and plants). The measurements per tree were performed in a quarter of the branches present and in 10 leaves present in each of the branches using a compass protractor as described by Norman and Campbell (1989).
Data analysis
The Beta (Goel and Strebel, 1984), ellipsoidal (Campbell, 1990) and de Wit (de Wit, 1965) classical distribution functions were compared with respect to the measurements of the leaf angle distribution recorded in the field for the upper, middle and lower profiles plus their combination. The de Wit functions were evaluated because the erectophile, planophile, plagiophile and extremophile distribution functions describe the trends of foliage orientation in general terms (de Wit, 1965). The Pearson Chi-square (χ2) statistical test determined the goodness of fit between data collected in the field and data estimated by the functions by indicating a better fit of the distributions with χ2 values closer to zero. The null hypothesis was confirmed (the leaf angle distribution measured in the field was not significantly different from the estimate based in one of the leaf angle distribution functions) for the χ2 test by verifying that the value of the χ2 statistic was less than χ2 (1-a; k-1) at 99% probability. The relationship between the observed value (dependent variable) and the estimated value (independent variable) was evaluated using statistically equal to one in the regression coefficient with a t-test at 1%. This procedure led to the conclusion that the estimated values do not overestimate or underestimate observed values. Additionally, root mean squares error (RMS) was used to demonstrate the goodness of fit according to Wang et al. (2007).
The leaf angle distribution recorded in the field from the profiles and their combination was described based on three classes of angles (1st class: 0°-30°, 2nd class: 30°-60°, and 3rd class: 60°-90°) according to Goudriaan (1988). The x parameter was used as a descriptor of the ellipsoidal leaf angle distribution function (Campbell, 1990), whereas the (v) and (μ) parameters were used for the Beta function (Goel and Strebel, 1984).
The statistical analyses were performed using the software SAS version 9.3 (SAS Institute, 2010) and the software Microsoft Excel (2010).
Results and discussion
The x2 test and the RMSE showed that the Beta function obtained the best fit in the middle and lower profiles of the tree and the combination of all three profiles, which the lowest X 2 values and RMSE values, although the ellipsoidal function showed the best fit only in the upper profile (Tab. 1). The foliage orientation described by the de Wit distribution functions showed that the upper and lower profiles were represented by the planophile function, whereas the middle profile was represented by the plagiophile function. The combination of all profiles was predominantly represented by the plagiophile function in accordance with the lowest X2 values and RMSE values, this without to consider the significance (Tab. 1). Mejía et al. (2013) found that 11 of the 19 coffee genotypes of C. arabica evaluated in their study were classified as plagiophile plants because they featured a high number of leaves with angles between 31° and 60°.
TABLE 1 Comparison of leaf angle distribution functions with the X2 test for the coffee variety Castillo® according to the tree profile.

++: distribution with the best fit according to the X2or RMSE criterion; ns: nosignificant difference in the X2 test at 99% probability (nuil hypothesis); **: significant differences in the X2test at 99% probability (alternative hypothesis); ns: coefficients significantly different equal one according to a t-testat 1%; **: coefficients significantly different from one according to a t-testat 1%.
The regression coefficient was statistically equal to one for the Beta and ellipsoidal functions in all profiles evaluated and in the combination. Additionally, it was confirmed for the plagiophile function in the lower profile. To test the null hypothesis, the significance of the X2 value was assessed by searching for nonsignificant X2 values. The null hypothesis was only confirmed for the Beta function in middle profile. Additionally, the null hypothesis for the plagiophile function in the lower profile was confirmed (Tab. 1). Based on the X2 values, regression coefficient and RMSE values, the Beta function with two parameters and the ellipsoidal function adequately described the leaf angle distribution present in the canopy of coffee variety Castillo®.
Overall, the performance of the Beta function with two parameters was better than that of the functions with one parameter (de Wit and ellipsoidal). In some plant species, the leaf angle distribution may have a dual structure mode or a diverse group of leaf area fractions with different leaf angles (Goel and Strebel, 1984; Wang et al., 2007). Wang et al. (2007) found that the X2 values of the Beta function were lower than those of the ellipsoidal function, indicating a better performance of the former in 33 of the 38 plant species tested. However, the ellipsoidal distribution function is widely used because it provides a reasonably accurate description of the empirical distribution of angles for actual plant canopies (Thomas and Winner, 2000).
The relative frequencies for the classes proposed by Goudriaan (1988) for the leaf angles measured in the field are shown in table 2. In all three profiles tested, the second class of leaf angles (30° to 60°) obtained the highest frequencies, with values between 45 and 50%. This finding indicates that the proportion of leaf angles between 30° and 60° throughout the canopy is relatively equal across the tree and predominant in the middle and upper canopy profiles (Tab. 2). Castillo et al. (1996) found that the range of angles from 0° to 30° obtained the highest recorded frequencies in all evaluated profiles for plants of the C. arabica Colombia variety, which was typical of planophile plants.
TABLE 2 Frequency of leaf angles according to three classes of angles and parameters of the ellipsoidal and Beta distribution functions for coffee variety Castillo® according to the tree profile.
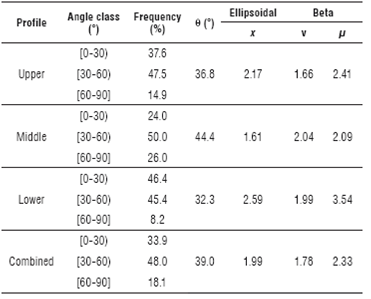
θ: mean leaf inclination angles in grades.
The relative frequencies of the first class of leaf angles (0° to 30°) were predominant only in the lower profile, with a value of 46.4%; in contrast, the middle profile obtained a proportion of only 24% for this class. Finally, the third class of leaf angles obtained the highest relative frequency in the middle profile, with a value of 26% (Tab. 2). This behavior was also reported by Castillo et al. (1996), who found that the upper middle tree profile obtained a lower relative frequency for the first class of leaf angles with respect to the other profiles. This result explains why the upper and lower profiles are classified as predominantly planophiles, whereas the middle profile is classified as predominantly plagiophile according to the best fit found by the de Wit functions (Tab. 1). In the combined profiles (Tab. 2), the highest relative frequency was observed in the second class of leaf angles (30°-60°), followed in order of magnitude by the first class (0°-30°) and finally by the third class (60°-90°); this finding classifies the canopy of C. arabica variety Castillo® as plagiophile by the criterion of de Wit (Tab. 1 and 2).
Data collected in the field showed that the upper and lower profiles with an x parameter greater than 2.0 mostly presented leaf angles with a tendency to be horizontal (mean angles less than 0 = 45°). In contrast, the middle profile with a value of x = 1.61 had a higher proportion of leaf angles with a vertical trend (mean angle greater than θ = 45°) with respect to the upper and lower profiles (Tab. 2). The combined profiles had a higher proportion of leaf angles tending to be horizontal, with a parameter x = 1.99 and an average angle of leaf inclination of 39.0° (Tab. 2). According to Goel and Strebel (1984), the value is greater than (v) in the planophile canopy type. This phenomenon is observed in data from C. arabica variety Castillo® for the upper, lower and combined profiles, with mean leaf inclination angles (θ) between 32.3° and 39.0° (Tab. 2). Moreover, the middle profile with very (μ) similar and (v) values greater than one predominantly represents a plagiophile canopy type (Tab. 2). Charbonnier et al. (2013) found that the coffee canopy had a plagiophile distribution based on the Beta distribution function, with parameters μ = 1.97 and v = 1.95.
One of the most successful methods to improve crop productivity is to increase the efficiency with which plants intercept solar radiation by altering the vertical distribution of solar radiation in the canopy. This phenomenon can be achieved with a more upright inclination angle of the leaves, which increases the gain in carbon by optimizing the interception of photosynthetically active radiation for canopy photosynthesis and mitigates the heat stress induced by excess infrared radiation (van Zanten et al., 2010; Song et al., 2013; Truong et al., 2015).
According to Blackman (1919), one of the most efficient canopy arrangements for the production of dry matter is the arrangement with erect leaves in the upper profiles that gradually become more horizontal; this pattern was observed for the middle and lower profiles in this study.
Canopies with predominantly horizontal leaves (planophiles) may limit photosynthesis in the lower profiles of many plants by intercepting most of the radiation in the upper profiles, thereby attenuating the rate of irradiance and thus the temperature inside the plant (Castillo et al., 1996; Castillo et al., 1997). However, this feature may be associated with the adaptation of the plant when exposed directly to sunlight (Castillo et al., 1996) as a protection mechanism to avoid saturation with relatively high irradiance.
In contrast, predominantly vertical canopies (erectophile) allow greater penetration of irradiance more evenly, thereby reducing senescence of the lower leaves by shading (Pearce et al., 1967; Sinclair and Sheehy, 1999; Song et al., 2013). For a coffee leaf, the saturation irradiance is relatively low, with values between 300 and 700 μmol m-2 s-1 (Kumar and Tieszen, 1980; Fahl et al., 1994). Inside the canopy of mature coffee trees, many leaves are partially or completely shaded and intercept only 1.5% of the total solar radiation, suggesting that canopy photosynthesis can become saturated when the irradiance is greater than 600-700 μmol m-2 s-1 (DaMatta et al., 2007). A better vertical redistribution of solar radiation through the canopy would allow higher seeding densities for grain crops, which is an important factor that increases the production of grain per hectare (Duvick 2005; Mansfield and Mumm, 2014).
Conclusions
The leaf angle distribution present in C. arabica variety Castillo® had the best fit for the Beta function with two parameters, followed by the ellipsoidal function. In these two distribution functions, the regression coefficient was statistically equal to one in all profiles evaluated. In Beta distribution function, the null hypothesis for the X2 test was only confirmed in middle profile. Given the diversity of leaf angles in fractions of leaf area per profile, the Beta function is suggested to be the most suitable to describe the canopy of the Castillo® variety. Another good choice for this purpose is the ellipsoidal function based on the obtained results. The ellipsoidal distribution function described the full canopy with an X parameter of 1.99, whereas the Beta distribution described the canopy with μ = 2.33 and v = 1.78, characterizing it as a planophile canopy. According to the de Wit functions, the canopy of C. arabica variety Castillo® better fits the plagiophile function. Knowing the leaf angle distribution functions that get better fitted to the leaf orientation in the canopy is important, because it allowes to simulate radiation distribution at different crop growth models.














