Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Iatreia
Print version ISSN 0121-0793
Iatreia vol.27 no.1 Medellín Jan./Mar. 2014
INVESTIGACIÓN ORIGINAL
Metodología diagnóstica geométrica fractal y euclidiana de células del cuello uterino
Fractal and Euclidean geometric diagnostic methodology of uterine cervix cells
Javier Oswaldo Rodríguez Velásque1; Signed Prieto Bohórquez2; Catalina Correa Herrera3; Yolanda Soracipa Muñoz4; Fernando Polo Nieto5; Laura Pinilla Bonilla6; Vanessa Blanco7; Andrés Camilo Rodríguez7
1 MD. Director del Grupo Insight. Fundación Universitaria de Ciencias de la Salud. Centro de Investigaciones de la Clínica del Country. Bogotá, Colombia. grupoinsight2025@yahoo.es
2 Investigadora del Grupo Insight. Fundación Universitaria de Ciencias de la Salud. Centro de Investigaciones de la Clínica del Country. Bogota, Colombia.
3 Psicóloga. Investigadora del Grupo Insight. Fundación Universitaria de Ciencias de la Salud. Centro de Investigaciones de la Clínica del Country, Bogotá, Colombia.
4 Licenciada en Física. Investigadora del Grupo Insight. Fundación Universitaria de Ciencias de la Salud. Centro de Investigaciones de la Clínica del Country. Bogotá, Colombia.
5 MD. Especialista en Patología. Líder del grupo de Investigación en Patología. Fundación Universitaria de Ciencias de la Salud. Bogotá, Colombia.
6 MD. Investigadora del Grupo Insight. Centro de Investigaciones de la Clínica del Country, Bogotá, Colombia.
7 Estudiante de la Facultad de Medicina, Fundación Universitaria de Ciencias de la Salud, Bogotá, Colombia.
Recibido: febrero 14 de 2013
Aceptado: agosto 06 de 2013
RESUMEN
Introducción: la interpretación patológica de las formas celulares halladas en la citología cervicovaginal es de gran importancia para la prevención del cáncer de cuello uterino. Los métodos más ampliamente utilizados para la evaluación de este examen presentan problemas de reproducibilidad y variabilidad interobservador.
Objetivo: hacer medidas fractales y euclidianas para diagnosticar matemáticamente células normales y preneoplásicas del epitelio escamoso del cuello uterino.
Metodología: se evaluaron 21 células con diagnósticos de normalidad, ASCUS o LIEBG según el sistema Bethesda. Se establecieron medidas geométricas fractales y euclidianas de tres objetos matemáticos definidos: citoplasma, núcleo y totalidad celular. Se calcularon proporciones matemáticas entre estas medidas con el fin de compararlas con los métodos convencionales de clasificación.
Resultados: se encontró que las medidas del borde con la rejilla de 2 pixeles y de la superficie del núcleo celular pudieron diferenciar matemática y objetivamente las células normales y las anormales, clasificadas como ASCUS y LIEBG, cuantificando la gravedad de la lesión.
Conclusiones: se estableció una metodología diagnóstica objetiva y reproducible que permite identificar la evolución hacia estados celulares de gravedad con base en medidas fractales y euclidianas simultáneas, estableciendo así el nivel de gravedad de las células ASCUS y LIEBG.
PALABRAS CLAVE
Biología Celular, Cuello del Útero, Diagnóstico, Neoplasias
SUMMARY
Background: Pathological interpretation of cellular form in cervical cytology is very important for prevention of cervical cancer. The methods most frequently used for assessment of this test have reproducibility and inter-observer variability problems.
Objective: To make fractal and Euclidean measurements to mathematically diagnose normal and premalignant cells of cervical squamous epithelium.
Methodology: 21 cells with normal, ASCUS or LSIL diagnosis according to the Bethesda system were assessed. Fractal and Euclidean geometric measures of three mathematical objects were calculated: cytoplasm, nucleus and whole cell. Mathematical proportions between these measurements were calculated in order to compare them with conventional classification methods.
Results: It was found that the nuclear border measures calculated with the 2-pixel grill and the surface measures could mathematically and objectively differentiate normal cells from the pre-malignant ones (ASCUS and LSIL).
Conclusions: An objective and reproducible diagnostic method was developed; it allows to identify the evolution towards malignant cellular states based on simultaneous fractal and Euclidean measures, establishing the severity level of ASCUS and LSIL cells.
KEY WORDS
Cervix Uteri, Cell Biology, Diagnosis, Neoplasms
INTRODUCCIÓN
El cáncer de cuello uterino ocupa el tercer lugar entre los tipos de cáncer más frecuentes en mujeres en el mundo, con una incidencia anual de 530.000 nuevos casos, según reportes del año 2008. Cada año más del 85% de los casos mundiales ocurren en países en desarrollo. En cuanto a la mortalidad, los reportes han indicado que anualmente mueren alrededor de 275.000 mujeres por esta razón (1). De acuerdo con los informes de la OMS del año 2008, en Colombia hubo alrededor de 2.000 muertes por cada 100.000 habitantes, lo que ubica el cáncer de cuello uterino en el cuarto lugar en el continente Americano (2).
La citología cervicovaginal se considera una herramienta crucial para la prevención secundaria mediante la detección de células anormales in situ antes de que progrese a una condición invasiva, lo que contribuye a la disminución de la mortalidad (3). En un estudio de Nanda y colaboradores se encontró que la sensibilidad de este examen diagnóstico era del 51% y su especificidad, del 98% (4). En la actualidad, el de Bethesda es el más ampliamente utilizado de los dos sistemas de clasificación patológica para el reporte de la citología cervicovaginal (5). Este sistema divide las lesiones escamosas en intraepiteliales de alto y bajo grado, además de tener una tercera categoría que corresponde a las células atípicas de significado indeterminado (ASCUS, por la sigla en inglés de atypical squamous cells of undetermined significance) (6). Esta última categoría se ha catalogado como la de menor reproducibilidad entre los observadores, y se ha posicionado como la de mayor reto diagnóstico (7-9).
La irregularidad de diferentes fenómenos (10), incluyendo las estructuras anatómicas y los sistemas fisiológicos del cuerpo humano (11-13), se puede estudiar desde la geometría fractal. La geometría euclidiana comenzó a evidenciar grandes limitaciones al pretender estudiar los objetos irregulares de la naturaleza de los diferentes campos previamente mencionados (14). La irregularidad de un objeto, cuando se estudia desde la geometría fractal, arroja un valor numérico llamado dimensión fractal (15). Se han desarrollado diferentes métodos para calcular esta dimensión de acuerdo con las características de diferentes objetos. Los objetos matemáticos abstractos se evalúan adecuadamente mediante la dimensión fractal de Hausdorff (16), mientras que los objetos de la naturaleza se pueden medir bien sea por el método de Box-counting (16,17), que permite caracterizar fractales salvajes, cuyas partes se superponen entre sí, o mediante distribuciones hiperbólicas como la ley de Zipf/Mandelbrot (18).
En el campo de la medicina las dimensiones fractales se han aplicado para el desarrollo de métodos para la detección del cáncer del seno (19,20), de la vejiga (21) y de la mucosa oral (22), entre otros (23-25). En el área de la morfología y la fisiología, se llevó a cabo un estudio que incluyó una generalización teórica que ha permitido establecer el número total posible de arterias normales, estenosadas y reestenosadas desde la geometría fractal y el concepto de armonía matemática intrínseca (AMI) (26). Además, se han desarrollado aplicaciones diagnósticas en ecocardiografía pediátrica (27), ventriculograma izquierdo (28) y en la ramificación coronaria (29,30).
En el área del estudio patológico de las células escamosas del cuello uterino se han desarrollado caracterizaciones matemáticas del grado de irregularidad de las células clasificadas como normales, ASCUS y LIEBG (lesión intraepitelial de bajo grado) (31). En estudios posteriores, se encontraron diferencias matemáticas entre células normales y LIEBG logrando diferenciar células clasificadas como ASCUS que tuvieran relaciones matemáticas de normalidad o de LIEBG (32) y, posteriormente, se logró establecer una generalización fractal que permite diferenciar las células normales de las preneoplásicas y cancerígenas por la determinación de todos los prototipos geométricos celulares cervicales; se logró, además, aclarar matemáticamente el diagnóstico problemático de las células de la franja ASCUS (33).
En un trabajo de Correa y colaboradores se estudió la morfofisiología del eritrocito a partir de la geometría fractal y euclidiana, y se logró diferenciar de manera objetiva los eritrocitos normales de los anormales. Se demostró que solo se podría llegar a establecer una diferenciación entre normalidad y anormalidad si se utilizaban de manera simultánea tanto la geometría fractal como la euclidiana (34), y se obtuvo una metodología de uso clínico para determinar la viabilidad de bolsas de transfusión.
El presente estudio tuvo como propósito la aplicación simultánea de la geometría fractal y euclidiana al estudio de células en estados de normalidad y evolución preneoplásica con el fin de establecer una metodología diagnóstica objetiva y reproducible de este fenómeno.
METODOLOGÍA
Definiciones
Fractal: como sustantivo hace referencia a un objeto irregular; como adjetivo señala la irregularidad del mismo.
Dimensión fractal: cuantificación de la irregularidad de un objeto. En la presente investigación se cuantificó la dimensión fractal con el método de Box-counting que se utiliza para el estudio de fractales salvajes (17). Este tipo de medición permite cuantificar los cambios de la irregularidad de un objeto al evaluarlo en diferentes escalas.
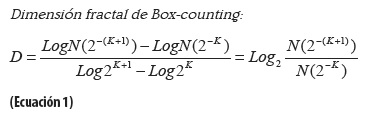
Donde: N: número de cuadros que contiene el contorno del objeto.
K: grado de partición de la cuadrícula.
D: dimensión fractal.
Superficie del objeto: corresponde al conteo de pixeles ocupados por cada uno de los objetos celulares definidos, ya sea el núcleo, el citoplasma o la totalidad.
Borde del objeto: corresponde al conteo de los cuadros ocupados por cada uno de los contornos de los objetos definidos en cada célula (núcleo, citoplasma y totalidad), utilizando las rejillas del método de Box-counting.
Procedimiento
Se seleccionaron 21 muestras citológicas del servicio de Patología del Hospital San José que fueron clasificadas por un citólogo experto de acuerdo con parámetros convencionales así: siete normales, siete ASCUS y siete LIEBG. Se escogieron las células por cumplir claramente con los criterios del diagnóstico en el que están clasificadas en el sistema Bethesda, con el fin de que fueran representativas de cada estado, de tal modo que su evaluación geométrica permitiera la determinación de las características matemáticas que representan cada uno de los grados de lesión evaluados.
Para el estudio de las muestras se utilizó un microscopio Leika Dm-2500 con un aumento de 100x. Se tomaron fotografías digitales de las células en láminas procesadas que se llevaron a una aplicación informática encargada de la edición de imágenes. Posteriormente, con un software previamente desarrollado, se calcularon las dimensiones fractales de tres objetos matemáticos definidos: el núcleo, el citoplasma aislado del núcleo y la totalidad celular. La dimensión fractal de Box-counting se calcula superponiendo rejillas de diferente magnitud, y cuantificando el número de cuadros que son ocupados por el borde de cada uno de los objetos medidos. En este caso se utilizaron rejillas de magnitud de 2, 4, 8, 16 y 32 pixeles. El software fue desarrollado en lenguaje C++. La función en la cual se basa el algoritmo permite identificar por coordenadas el número de cuadros que ocupa el borde de la imagen seleccionada en cada rejilla, retornando el valor obtenido para cada imagen y cada rejilla. Con base en los valores obtenidos para las cinco rejillas el programa calcula la dimensión fractal mediante la ecuación de Box-counting (ver definiciones). Además, el programa permite la visualización del número de espacios ocupados por la superficie de la imagen, en pixeles, datos que fueron anotados para su posterior análisis. La dimensión de Box-counting es el resultado del cálculo de la pendiente de la recta construida con los puntos que en el eje de coordenadas cartesianas corresponden a los logaritmos del número de cuadros que ocupa el borde del objeto medido y del inverso multiplicativo del ancho del cuadro, lo cual implica que se requiere la medición de varias cuadrículas para su aplicación. Suele resultar conveniente que la proporción entre el ancho de una cuadrícula y el de la siguiente sea de ½, razón por la cual se escogieron las rejillas de 32, 16, 8, 4 y 2 mm.
Finalmente, se establecieron las diferencias matemáticas entre cada uno de los estados estudiados para diferenciar estadios celulares basados en geometría fractal y euclidiana. Por el tipo de metodología desarrollado, basado en medidas geométricas objetivas y reproducibles de células representativas de cada estado evaluado, no se requiere un gran número de muestras ni de procedimientos estadísticos.
RESULTADOS
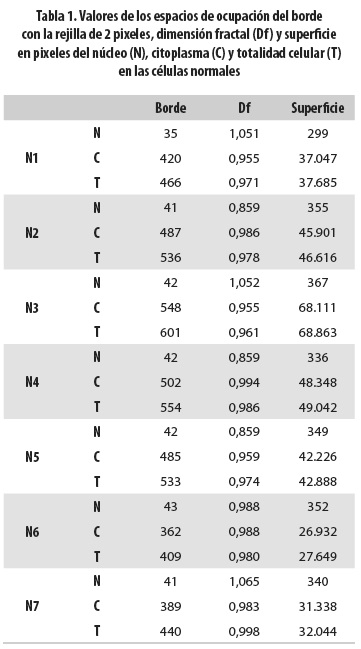
Con base en el análisis de las medidas del borde obtenidas en cada una de las rejillas, se estableció que la de dos pixeles es la más adecuada para establecer las diferencias entre grupos, por su nivel de detalle. Por esta razón solo se presentan los resultados obtenidos para dicha rejilla.
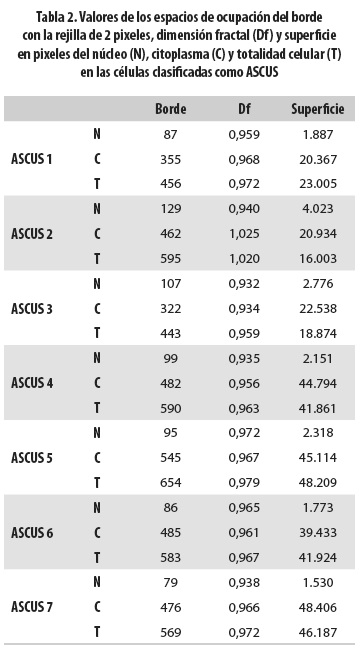
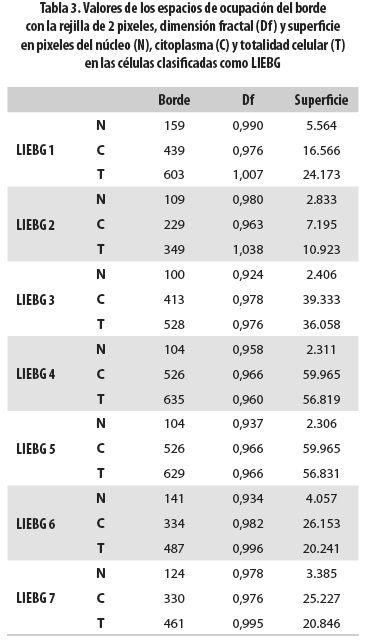
Los valores del borde del núcleo de las células normales estuvieron entre 35 y 43, mientras que los hallados para las células clasificadas como ASCUS se encontraron entre 79 y 129, y para las células clasificadas como LIEBG estuvieron entre 100 y 159. Se observa que estos valores permiten diferenciar de manera objetiva las células normales de aquellas clasificadas como ASCUS y LIEBG. Con respecto a estos dos últimos grupos, se evidenció que cinco de las células ASCUS medidas presentaron valores inferiores a 100, que es el límite inferior del intervalo de valores hallado para las células LIEBG, mientras que dos células ASCUS presentaron valores dentro del intervalo de LIEBG. Esto significa que no hay características matemáticas claras que diferencien las células ASCUS; sin embargo, el hecho de que las células ASCUS presenten valores en el rango intermedio entre normalidad y LIEBG, y que en dos casos estos valores se superpongan a los característicos de LIEBG, es un indicador de que la progresión en el aumento de los valores desde normalidad hasta LIEBG indica un aumento del grado de la lesión. Con base en esto puede inferirse que los valores iguales o inferiores a 43 se asocian a normalidad, mientras que los superiores a 100 se asocian a LIEBG, en tanto que las células ASCUS podrán encontrarse en el rango intermedio entre normalidad y LIEBG, o bien tomar valores característicos de LIEBG (tablas 1,2,3).
Para el borde del citoplasma no se encontraron diferencias en los valores entre los tres estadios; en efecto, los de las células normales estuvieron entre 362 y 548; los de las células ASCUS, entre 322 y 545; y los de las células con LIEBG, entre 229 y 526. Para la totalidad celular tampoco se encontraron valores diferenciadores: los de las células normales estuvieron entre 409 y 601; los de las células ASCUS, entre 443 y 654; y los de las células LIEBG, entre 349 y 635 (tablas 1-3).
En el caso de la superficie del núcleo, los valores encontrados también permitieron establecer una diferencia objetiva entre las células consideradas normales y aquellas clasificadas como ASCUS y LIEBG: entre 229 y 367 para las células normales; entre 1.530 y 4.023 para las clasificadas como ASCUS y entre 2.306 y 5.564 para las clasificadas como LIEBG, con superposición también entre estos dos últimos estadios celulares.
Para la superficie del citoplasma no se encontraron valores diferenciadores: las células normales los tuvieron entre 26.932 y 68.111; las células ASCUS, entre 20.367 y 48.406; y las células clasificadas como LIEBG, entre 7.195 y 59.965. Para la superficie de la totalidad de la célula tampoco se hallaron diferencias: los valores estuvieron entre 27.649 y 68.863 para las células normales; entre 16.003 y 48.209 para las células ASCUS y entre 10.923 y 56.831 para las LIEBG (tablas 1-3).
En el caso de la dimensión fractal de los tres grupos celulares no se encontraron diferencias en los valores; ellos fueron: entre 0,859 y 1,065 para las células normales; entre 0,932 y 1,025 para las células ASCUS y entre 0,924 y 1,038 para las células LIEBG.
DISCUSIÓN
Este es el primer trabajo en que se utilizan de manera simultánea la geometría fractal y la euclidiana para diferenciar las células normales del cuello uterino, las ASCUS y aquellas con lesión intraepitelial de bajo grado (LIEBG). Las medidas obtenidas del borde del núcleo celular permiten establecer una diferenciación clara entre las células normales y las anormales (ASCUS y LIEBG), e indican además que una elevación de este valor puede asociarse a un aumento en el grado de severidad de la lesión; así se logra un método objetivo y reproducible respecto al sistema Bethesda, que aclara el nivel de gravedad de las células ASCUS.
Las células evaluadas se escogieron de tal modo que no presentaran dudas en su diagnóstico, pues el objetivo de este trabajo era lograr medidas objetivas y reproducibles de un fenómeno que usualmente se mide con parámetros cualitativos y que, por lo tanto, está sometido a la subjetividad del experto, con el fin de superar los problemas de reproducibilidad que implican los métodos actuales. Por esta razón era necesario un enfoque diferente del fenómeno, fundamentado en una forma de razonamiento físicomatemático inductivo, en la que a partir de unos pocos casos seleccionados por contener la totalidad de las condiciones evaluadas para cada estado, sea posible establecer características geométricas objetivas del comportamiento celular de acuerdo con el grado de evolución de la lesión, con base en pocas muestras e independientemente de consideraciones estadísticas. Al evaluar con la rejilla de dos pixeles el borde del núcleo de las células clasificadas como ASCUS se encontraron valores en un rango intermedio entre la normalidad y las LIEBG en cinco de los siete casos, mientras que los dos restantes presentaron valores matemáticos característicos de LIEBG. Dada la dificultad de diagnosticar con claridad las células ASCUS con los parámetros convencionales, era previsible que no pudieran establecerse con total especificidad rangos diferenciales para tal estado. Sin embargo, el hecho de que en la mayoría de los casos sus valores se encuentren en el rango intermedio, y que dos presenten valores característicos de LIEBG, confirma la conclusión de que el aumento del valor del borde nuclear es un indicador de que se está ante un caso de mayor gravedad, independientemente de si la célula se evalúa de forma cualitativa como ASCUS o LIEBG, lo que es de gran utilidad clínica en los procesos de detección temprana de casos en evolución hacia neoplasias del cuello uterino. En este sentido es importante el desarrollo de aplicaciones ulteriores de esta metodología a un mayor número de casos para corroborar los límites encontrados y poder lograr cada vez una mayor exactitud de las medidas.
En el sistema Bethesda, y en otros similares aceptados convencionalmente, uno de los parámetros observados usualmente de forma cualitativa es el tamaño del núcleo (35), pero estos sistemas exigen la observación simultánea de varios de estos parámetros; ello plantea problemas de reproducibilidad, al no contar con un método para medir objetivamente el borde nuclear (36). En contraposición, el presente método evalúa de manera objetiva el cambio en el tamaño de dicho borde y tiene en cuenta, además, su carácter geométrico irregular.
La metodología diagnóstica utilizada en este trabajo, al igual que las empleadas previamente a partir de la geometría fractal y el concepto de variabilidad y AMI celular (32,33), permite identificar de manera objetiva y reproducible diferencias entre normalidad y anormalidad (ASCUS y LIEBG), y señala además cuándo una célula ASCUS se encuentra más cercana a tener valores de normalidad o bien de LIEBG. Es relevante que para futuras investigaciones se determine el impacto de la aplicación de la metodología desarrollada por Rodríguez y colaboradores (32,33), que se basa en la variabilidad fractal y la AMI celular junto con las medidas halladas en la presente investigación.
Por otra parte, si se considera la hipótesis del origen genético del cáncer, en la que se establece que las neoplasias parten de la amplificación clonal de una célula única que ha sufrido una alteración genética y exhibe un cambio del núcleo (37), es posible inferir que los resultados de la presente investigación apoyan indirectamente esta hipótesis dado que se verifican cambios morfológicos en el núcleo. Sin embargo, independientemente de si esta inferencia es correcta, la metodología utilizada en este trabajo se basa en una forma de pensamiento físico que hace abstracción de las relaciones causa-efecto, al evidenciar solamente características geométricas asociadas a cada estado, independientemente de factores de riesgo y análisis estadísticos. Este tipo de mediciones representa una línea de investigación que puede ser de gran utilidad y relevancia para lograr una diferenciación objetiva y cuantitativa de células en estadios preneoplásicos y neoplásicos, y que será contrastada en trabajos futuros con otras metodologías para establecer su eficacia respecto a otros métodos de evaluación.
AGRADECIMIENTOS
Este trabajo es resultado del proyecto 71-3743-5, de la segunda convocatoria del 2012, financiado por la División de Investigaciones de la Fundación Universitaria de Ciencias de la Salud-Hospital de San José, por lo cual agradecemos su apoyo y confianza. De la misma manera, agradecemos al doctor Guillermo Sánchez, Director de la División de Investigaciones; a la doctora Magda Alba, Coordinadora de Investigaciones de Posgrado; al doctor Carlos Escobar, Gestor del Conocimiento, y a Nataly Preciado, Coordinadora de Convocatoria Interna, por todo el apoyo y la confianza depositada en el Grupo Insight.
Agradecemos también al Centro de investigaciones de la Clínica del Country; al doctor Tito Tulio Roa, Director de Educación Médica; al doctor Alfonso Correa, Director del Centro de Investigaciones; al doctor Jorge Ospina, Director Médico; a la doctora Adriana Lizbeth Ortiz, Epidemióloga, y a Silvia Ortiz, por el apoyo brindado en todos estos años a nuestro trabajo.
Dedicación
A nuestros hijos.
REFERENCIAS BIBLIOGRÁFICAS
1. International Agency for Research on Cancer, World Health Organization. Cervical Cancer Incidence, Mortality and Prevalence Worldwide in 2008 Summary [Internet]. 2008 (cited 2013 Jan 14). p. 2. Available from: http://globocan.iarc.fr/factsheet.asp [ Links ]
2. International Agency for Research on Cancer, World Health Organization. Globocan 2008: estimated cancer Incidence, Mortality, Prevalence and Disability- adjusted life years (DALYs) Worldwide in 2008 [Internet]. 2008 (cited 2013 Jan 14). Available from: International Agency for Research on Cancer [ Links ]
3. Weiderpass E, Labrèche F. Malignant tumors of the female reproductive system. Saf Heal. Work. 2012 Sep;3(3):166–80. [ Links ]
4. Nanda K, McCrory DC, Myers ER, Bastian LA, Hasselblad V, Hickey JD, et al. Accuracy of the Papanicolaou test in screening for and follow-up of cervical cytologic abnormalities: a systematic review. Ann Intern Med. 2000 May 16;132(10):810–9. [ Links ]
5. Dim CC. Towards improving cervical cancer screening in Nigeria: a review of the basics of cervical neoplasm and cytology. Niger J Clin Pr. 2012;15(3):247–52. [ Links ]
6. Apgar BS, Zoschnick L, Wright TC. The 2001 Bethesda System terminology. Am Fam Physician. 2003 Nov 15;68(10):1992–8. [ Links ]
7. Smith AE, Sherman ME, Scott DR, Tabbara SO, Dworkin L, Olson J, et al. Review of the Bethesda System atlas does not improve reproducibility or accuracy in the classification of atypical squamous cells of undetermined significance smears. Cancer. 2000 Aug 25;90(4):201–6. [ Links ]
8. Stoler MH, Schiffman M. Interobserver reproducibility of cervical cytologic and histologic interpretations: realistic estimates from the ASCUS-LSIL Triage Study. JAMA. 2001 Mar 21;285(11):1500–5. [ Links ]
9. Lachman MF, Cavallo-Calvanese C. Qualification of atypical squamous cells of undetermined significance in an independent laboratory: is it useful or significant? Am J Obs. Gynecol. 1998 Aug;179(2):421–9. [ Links ]
10. Mandelbrot B. The fractal geometry of nature. San Francisco: Freeman; 1972. [ Links ]
11. Gazit Y, Baish JW, Safabakhsh N, Leunig M, Baxter LT, Jain RK. Fractal characteristics of tumor vascular architecture during tumor growth and regression. Microcirculation. 1997 Dec;4(4):395–402. [ Links ]
12. Goldberger AL, Rigney DR, West BJ. Chaos and fractals in human physiology. Sci Am. 1990 Feb;262(2):42–9. [ Links ]
13. Goldberger AL. Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. Lancet. 1996 May 11;347(9011):1312–4. [ Links ]
14. Mandelbrot B. ¿Cuánto mide la costa de Gran Bretaña? In: Mandelbrot B, editor. Los objetos fractales. Barcelona: Tusquets; 2000. p. 27–50. [ Links ]
15. Mandelbrot B. Introducción. In: Mandelbrot B, editor. Los objetos fractales. Barcelona: Tusquets; 2000. p. 13–26. [ Links ]
16. Peitgen O, Jürgens H, Dietmar S. Limits and selfsimilarity. In: Peitgen O, Jürgens H, Dietmar S, editors. Chaos and fractals. New York: Springer-Verlag; 1992. p. 135–182. [ Links ]
17. Peitgen O, Jürgens H, Dietmar S. Length area and dimension: measuring complexity and scalling properties. In: Peitgen O, Jürgens H, Dietmar S, editors. Chaos and fractals. New York: Springer-Verlag; 1992. p. 183–228. [ Links ]
18. Rodríguez J. Dynamical systems theory and ZIPF – Mandelbrot Law applied to the development of a fetal monitoring diagnostic methodology. XVIII Figo World Congr. Gynecol. Obstet. Kuala Lumpur, Malaysia: FIGO; 2006. [ Links ]
19. Pohlman S, Powell KA, Obuchowski NA, Chilcote WA, Grundfest-Broniatowski S. Quantitative classification of breast tumors in digitized mammograms. Med Phys. 1996 Aug;23(8):1337–45. [ Links ]
20. Lefebvre F, Benali H, Gilles R, Kahn E, Di Paola R. A fractal approach to the segmentation of microcalcifications in digital mammograms. Med Phys. 1995 Apr;22(4):381–90. [ Links ]
21. Luzi P, Bianciardi G, Miracco C, De Santi MM, Del Vecchio MT, Alia L, et al. Fractal analysis in human pathology. Ann N Y Acad Sci. 1999 Jun 30;879:255–7. [ Links ]
22. Landini G, Rippin JW. Fractal dimensions of the epithelial- connective tissue interfaces in premalignant and malignant epithelial lesions of the floor of the mouth. Anal Quant Cytol Histol. 1993 Apr;15(2):144–9. [ Links ]
23. West J. Fractal physiology and chaos in medicine. World Sci. Singapore; 1990. [ Links ]
24. Goldberger AL, Amaral LAN, Hausdorff JM, Ivanov PC, Peng C-K, Stanley HE. Fractal dynamics in physiology: alterations with disease and aging. Proc Natl Acad Sci U S A. 2002 Feb 19;99 Suppl 1:2466–72. [ Links ]
25. Baish JW, Jain RK. Fractals and cancer. Cancer Res. 2000 Jul 15;60(14):3683–8. [ Links ]
26. Rodríguez JO, Prieto SE, Correa C, Bernal PA, Puerta GE, Vitery S, et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Med Phys. 2010 Jan;10:1. [ Links ]
27. Rodríguez J, Prieto S, Ortiz L, Ronderos M, Correa C. Diagnóstico matemático de ecocardiografías pediátricas con medidas de dimensión fractal evaluadas con armonía matemática intrínseca. Rev Colomb Cardiol. 2010;17(2):79–86. [ Links ]
28. Rodríguez J, Prieto S, Correa C, Bernal P, Álvarez L, Forero G et al. Diagnóstico fractal del ventriculograma cardiaco izquierdo. Geometría fractal del ventriculograma durante la dinámica cardiaca. Rev Colomb Cardiol. 2012; 19(1):18-24. [ Links ]
29. Rodríguez J, Álvarez LF, Mariño ME, Avilán G, Prieto S, Casadiego E, et al. Variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa. Geometría fractal del ventriculograma durante la dinámica cardiaca. Rev Colomb Cardiol. 2004;11(4):185–192. [ Links ]
30. Rodríguez J, Prieto S, Ortiz L, Correa C, Álvarez L, Bernal P, et al. Variabilidad de la dimensión fractal de la ramificación coronaria izquierda en ausencia y presencia de enfermedad arterial oclusiva moderada y severa. Rev Colomb Cardiol. 2007;14(3):173–179. [ Links ]
31. Rodríguez J, Prieto S, Ortiz L, Correa C, Wiesner C, Díaz M. Descripción matemática con dimensiones fractales de células normales y con anormalidades citológicas de cuello uterino. Rev. Cienc. Salud. 2006;4(2):58–63. [ Links ]
32. Rodríguez J. Nuevo método fractal de ayuda diagnóstica para células preneoplásicas del epitelio escamoso cervical. Rev. U.D.C.A Act. Div. Cient. 2011;14(1):15–22. [ Links ]
33. Rodriguez J, Prieto S, Correa C, Posso H, Bernal P, Puerta G. Generalización fractal de células preneoplásicas y cancerígenas del epitelio escamoso cervical de aplicación clínica. Rev fac med. 2010;18(2):173–81. [ Links ]
34. Correa C, Rodríguez J, Prieto S, Álvarez L, Ospino B, Munévar Á, et al. Geometric diagnosis of erythrocyte morphophysiology. J Med Med Sci. 2012;3(11):715–20. [ Links ]
35. Schmidt JL, Henriksen JC, McKeon DM, Savik K, Gulbahce HE, Pambuccian SE. Visual estimates of nucleus-to-nucleus ratios: can we trust our eyes to use the Bethesda ASCUS and LSIL size criteria? Cancer. 2008 Oct 25;114(5):287–93. [ Links ]
36. Lacruz Pelea C. Nomenclatura de las lesiones cervicales (de Papanicolau a Bethesda 2001). Rev Esp Patol. 2003;36(1):5–10. [ Links ]
37. DeVita V, Hellman S, Rosenberg S, editors. Cáncer: principios y práctica de oncología. 5th ed. Bogotá D.C.: Editorial Medica Panamericana, ARAN ediciones S.A; 2000. [ Links ]