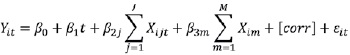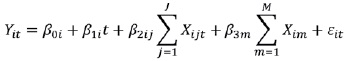Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Iatreia
Print version ISSN 0121-0793
Iatreia vol.28 no.3 Medellín July/Aug. 2015
https://doi.org/10.17533/udea.iatreia.v28n3a12
ACTUALIZACIÓN CRÍTICA
DOI 10.17533/udea.iatreia.v28n3a12
Ronda clínica y epidemiológica. Análisis de datos longitudinales
Clinical and epidemiological round. Longitudinal data analysis
Ronda clínica e epidemiológica. Análise de dados longitudinais
Alba Luz León A.1; Fabián Jaimes Barragán2
1 Profesora de cátedra, Facultad Nacional de Salud Pública, Universidad de Antioquia. Grupo Académico de Epidemiología Clínica (GRAEPIC), Medellín, Colombia.
2 Profesor Titular, Grupo Académico de Epidemiología Clínica (GRAEPIC), Departamento de Medicina Interna, Facultad de Medicina, Universidad de Antioquia. Investigador, Unidad de Investigaciones, Hospital Pablo Tobón Uribe, Medellín, Colombia. fabian.jaimes@udea.edu.co
Financiación: trabajo apoyado parcialmente por la Estrategia de Sostenibilidad de la Universidad de Antioquia, 2013-2014.
Recibido: mayo 04 de 2015
Aceptado: mayo 11 de 2015
RESUMEN
El denominado análisis de datos longitudinales (ADL) se refiere a los métodos para evaluar de manera apropiada las medidas de un mismo sujeto que se repiten en el tiempo. El ADL es una herramienta adecuada para entender indicadores de cambio en procesos de salud y enfermedad y para la evaluación del efecto de diversas intervenciones terapéuticas. Se presentan los principales modelos de ADL, sus ventajas y algunos ejemplos recientes de la literatura médica.
PALABRAS CLAVE
Análisis de Datos Longitudinales, Ecuaciones Generales de Estimación, Medidas Repetidas, Modelos de Efectos Mixtos
SUMMARY
Longitudinal data analysis (LDA) refers to the methods designed to evaluate repeated measurements within an individual. LDA is an appropriate tool to address the process of change in health and disease and also to evaluate the efficacy of interventions. We present the main LDA models as well as their advantages and some clinical examples from recent medical literature.
KEY WORDS
Longitudinal Data Analysis, General Estimating Equations, Mixed Models, Repeated Measurements
RESUMO
A denominada análise de dados longitudinais (ADL) refere-se aos métodos para avaliar de maneira apropriada as medidas de um mesmo sujeito que se repetem no tempo. O ADL é uma ferramenta adequada para entender indicadores de mudança em processos de saúde e doença e para a avaliação do efeito de diversas intervenções terapêuticas. Apresentam-se os principais modelos de ADL, suas vantagens e alguns exemplos recentes da literatura médica.
PALAVRAS CHAVE
Análises de Dados Longitudinais, Equações Gerais de Estimação, Medidas Repetidas, Modelos de Efeitos Mistos
Cómo citar: León AL, Jaimes Barragán F. Ronda clínica y epidemiológica. Análisis de datos longitudinales. Iatreia. 2015 Jul-Sep;28(3): 332-340. DOI 10.17533/udea.iatreia.v28n3a12.
INTRODUCCIÓN
Para el conocimiento y la investigación hoy en día es cada vez más común la necesidad de evaluar el comportamiento de algunas variables a lo largo del tiempo; y a partir de los cambios que se observen en los valores de dichas variables, establecer un posible patrón o tendencia que sea capaz de representar esos resultados de una manera reproducible. Específicamente en el ámbito de la salud y las ciencias biomédicas, frecuentemente son necesarias la evaluación y comprensión de múltiples medidas secuenciales de diferentes variables en un mismo individuo, por ejemplo, las características clínicas de un paciente en la evolución de su enfermedad o los resultados de pruebas de laboratorio que deben repetirse periódicamente, entre otros. El denominado análisis de datos longitudinales (ADL) comprende los métodos para evaluar de manera apropiada las medidas de un mismo sujeto que se repiten en el tiempo (1).
GENERALIDADES
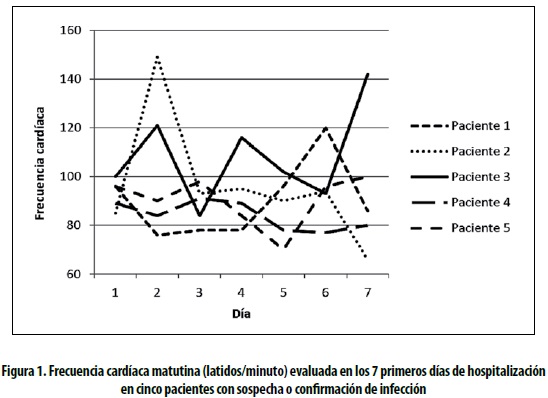
Como fundamentación para los conceptos posteriores, en la figura 1 se observan los valores de la frecuencia cardíaca durante la primera semana de hospitalización en cinco pacientes incluidos en la investigación La Epidemiología de la Sepsis en Colombia (2). Para el ADL la variable de respuesta, o aquella cuyo cambio se quiere estimar, es la frecuencia cardíaca; las unidades básicas de observación o análisis son los pacientes y el tiempo en el cual se espera observar una tendencia es la semana, cuya unidad de medida en este caso es en días.
El gráfico permite observar la variabilidad o diferencia existente en la frecuencia cardíaca entre diferentes pacientes y a la vez la variabilidad de esta misma frecuencia dentro de cada paciente a lo largo del tiempo, en este caso los días de medición. Una primera consideración es que la frecuencia cardíaca de cada día en cada paciente es más cercana a los valores de ese mismo paciente en los días inmediatamente anteriores o posteriores. En el paciente 1, por ejemplo, la frecuencia cardíaca registrada el día 3 es de alguna forma ''el resultado'' de las frecuencias cardíacas presentadas en los días previos. Dicho de otro modo, es de esperar que las frecuencias cardíacas de días sucesivos (días 5 y 6 en el paciente 2) sean más similares entre ellas que si se comparan con la frecuencia cardíaca registrada en días más alejados (día 2 del mismo paciente). Lo anterior define un hecho fundamental en este tipo de datos y es la particularidad de que las observaciones están correlacionadas, o mejor, no son independientes entre sí. Otra claridad que permite hacer este gráfico, y que está directamente ligada a la consideración anterior, es que los datos se presentan de una manera jerárquica o están organizados en una estructura de al menos dos niveles (''multinivel''). Como un primer nivel se puede considerar las observaciones realizadas en cada paciente en los diferentes días de observación, en este caso 7 días; y en un segundo nivel se puede considerar a los diferentes pacientes, en este caso cinco, en quienes se hacen las respectivas mediciones de frecuencia cardíaca. Lo anterior, bajo esta estructura de datos longitudinales, implica considerar que cada individuo tendrá una serie de observaciones que pueden representarse como su propia ''ecuación de regresión'' (3).
Lo más importante que se desea estimar con este tipo de análisis es el cambio que experimenta la variable de resultado en el tiempo, aunque, dependiendo de la pregunta de investigación que se plantee, puede no interesar el aumento o la reducción de la característica estudiada sino su estabilidad a lo largo del tiempo (4). Como se explicó previamente, el hecho de que se mida la misma variable en los mismos sujetos en distintos momentos implica que las diferentes medidas realizadas no cumplen con uno de los supuestos básicos de las técnicas tradicionales de análisis de datos: ''la independencia entre las observaciones'' (5). Aunque la existencia de más de dos medidas repetidas sobre una misma unidad de análisis, en este caso pacientes, permite evaluar cambios y transiciones entre diferentes estados de salud, también implica considerar, además de la correlación entre observaciones mencionada anteriormente, el cambio de variabilidad (varianza) debido al efecto ''tiempo'' que dificulta la precisión del modelo y el potencial desequilibrio en el número de observaciones debido a que un individuo puede no estar presente durante todo el seguimiento (6).
ANÁLISIS TRADICIONAL PARA DATOS LONGITUDINALES
Hasta finales de los años 80 era común encontrar en la literatura biomédica el análisis de este tipo de datos por medio de técnicas tradicionales como el análisis de la varianza (ANOVA) para medidas repetidas y el análisis multivariante de la varianza (MANOVA) (7). No obstante, como desventajas del empleo de estas técnicas se puede mencionar, entre otras las siguientes:
• No permiten analizar variables de respuesta, es decir, los desenlaces repetidos de tipo ordinal ni nominal.
• Para las variables de respuesta cuantitativas se debe cumplir con el supuesto de la normalidad, o distribución de Gauss, de dicha variable.
• Solo permite estimar el efecto de una variable independiente, usualmente el tiempo, en el cambio de la variable de resultado o de respuesta.
• Se debe disponer del conjunto de datos completo sin pérdida de mediciones u observaciones.
• Los intervalos de tiempo deben ser constantes.
• No consideran el problema de correlación entre las observaciones (8-10). De acuerdo con las anteriores consideraciones, excepcionalmente es posible lograr un conjunto de datos que cumpla con los requisitos para poder usar de manera eficaz las técnicas convencionales de análisis.
ANÁLISIS ACTUAL PARA DATOS LONGITUDINALES
Gracias a los avances significativos en los métodos estadísticos y computacionales, actualmente el análisis de este tipo de datos se lleva a cabo desde la perspectiva del modelo lineal generalizado (MLG), que no es otra cosa que la definición de una estructura común sobre la base de la ecuación tradicional de la línea recta (y = a + bx). Con esta estructura o ecuación común, y con diferentes funciones de enlace, el MLG permite unificar diversos modelos estadísticos como la regresión lineal, la regresión logística y la regresión de Poisson bajo un solo marco conceptual (11). De este modo, las ventajas analíticas son múltiples:
• Es posible modelar cualquier tipo de variable de desenlace.
• Permite el uso completo de los datos disponibles, aun teniendo en cuenta valores faltantes, lo que produce estimaciones más robustas y confiables (5).
• Permite estimar y diferenciar la variación entre las unidades de análisis y también la variación dentro de las unidades de análisis.
• Permite estimar, de manera simultánea, al igual que en todos los análisis multivariables, el efecto de cualquier tipo de variable independiente en el cambio de la variable de resultado. Adicionalmente, permite involucrar también los cambios temporales o la evolución de las variables independientes (4).
• De acuerdo con los objetivos del estudio, permite realizar tanto inferencias poblacionales como individuales o condicionales en la relación entre mediciones e individuos.
• Permite diferenciar fenómenos de corto, mediano y largo plazo (12).
• Al ser más estricto en la selección del modelo que mejor se ajusta a los datos, también es estadísticamente más potente (13).
• Suministra información sobre fenómenos acumulativos para poder establecer el comienzo, la duración y el final de un suceso.
Específicamente en el área de la salud, estas ventajas se pueden resumir así:
• Proporcionan información sobre la historia natural o el curso clínico de la enfermedad.
• Estudian la persistencia o no, además de la estabilidad, de una enfermedad.
• Analizan acontecimientos vitales del curso natural de una condición.
• Clarifican los efectos de las intervenciones realizadas en un paciente.
El ADL, dentro de esta nueva definición de un MLG, se clasifica en tres grandes ''familias'' o grupos y la elección del tipo de modelo necesario para obtener la estimación del cambio esperado en la variable de resultado depende de la clase de datos disponibles, de la pregunta de investigación que se desee resolver y de los recursos de software con los que se cuenta para el análisis, entre otros (14-16):
1. Los modelos especificados condicionalmente o modelos de transición: tienen en cuenta para modelar la distribución de la variable de resultado en su ocurrencia actual, la misma ocurrencia de la variable de resultado en las observaciones pasadas además de toda la información de las variables independientes (17). Es decir, la variable de resultado en el tiempo i está condicionada o es explicada por los valores de esa misma variable de resultado en el tiempo i-1, además de todas las otras variables independientes que se consideren. En estos modelos de transición, conocidos también como modelos de Markov, la distribución condicionada de cada respuesta se expresa como una función explícita de las respuestas pasadas y de las variables explicativas. La dependencia entre las medidas repetidas se debe a la influencia de los valores pasados de la respuesta en la observación actual (18). En el ejemplo inicial, la frecuencia cardíaca promedio esperada de la población de estudio en el día 7 depende de los valores de dicha frecuencia en el día 6 y de cualquier otra variable explicativa que se considere; la distribución de los valores de frecuencia cardíaca del día 6 está condicionada por los valores del día 5, y así sucesivamente. En general, estos modelos de transición son más difíciles de aplicar cuando hay datos faltantes o mediciones en intervalos de tiempo que no son equidistantes.
2. Los modelos marginales: se concentran en la relación entre el valor de la variable de resultado en cada momento del tiempo y las variables independientes, ajustando por separado la asociación entre los valores correspondientes a un mismo individuo. El término ''marginal'' en este contexto se usa para enfatizar que el interés principal es modelar la respuesta esperada o promedio; y que en cada momento de tiempo i dicha respuesta promedio depende solamente de las covariables de interés y no de respuestas previas como en los modelos de Markov o de cualquier efecto aleatorio como en los modelos mixtos (ver adelante) (14,15). Típicamente, además del contexto habitual del promedio esperado y la varianza en un MLG, los modelos marginales tienen en cuenta la falta de independencia entre las observaciones al modelar también separadamente la asociación dentro de los sujetos entre las respuestas repetidas del mismo individuo. Esta separación de la respuesta promedio esperada y la asociación entre las respuestas implica que los parámetros que se estiman de la regresión (los coeficientes) corresponden a valores promediados para el total de la población. Esos coeficientes describen el cambio en el tiempo de la respuesta promedio en la población y la manera como ese cambio es afectado por las variables explicativas. Un ejemplo de modelos marginales son las ecuaciones estimables generalizadas (General Estimating Equations, GEE) (19). En el ejemplo inicial, el cambio en la frecuencia cardíaca promedio de los individuos durante la primera semana podría depender de otras variables como la edad, el sexo o el tipo de infección, pero no de las frecuencias cardíacas de los días previos ni de efectos aleatorios no conocidos.
3. Los modelos específicos del individuo o modelos de efectos aleatorios: se diferencian de los modelos marginales, también conocidos como modelos de población promedio, por la inclusión de parámetros específicos de los individuos; para lo cual el efecto específico del individuo es una variable aleatoria que no está asociada ni correlacionada con las variables independientes o explicativas. En estos modelos, la respuesta media esperada en la variable de resultado está condicionada tanto por las variables independientes como por los efectos aleatorios no observados, y es la inclusión de estos últimos la que ''induce'' o explica la correlación entre las medidas repetidas. Existen modelos de este tipo, también denominados modelos de efectos mixtos por su combinación de componentes individuales y promedio, para variables de resultado continuas, binarias, de persona-tiempo o desenlaces de tiempo hasta el evento (18). En el ejemplo inicial, nuevamente, el cambio en la frecuencia cardíaca de los individuos en cada día durante la primera semana depende de otras variables como la edad o el sexo, pero también de efectos específicos individuales no cuantificados de manera explícita como variaciones genéticas o tipos de respuesta del sistema nervioso autónomo, entre otros.
FORMULACIÓN DE LOS MODELOS
El ADL, en general, mide los cambios de una variable en función del tiempo por medio de un MLG (20). Dicho modelo, a su vez, tiene diferencias en su formulación de acuerdo con las consideraciones que se explicaron previamente acerca de la correlación entre las observaciones o los efectos aleatorios individuales. La formulación matemática para los modelos más comúnmente usados de tipo marginal (el GEE) y de efectos mixtos se presenta a continuación.
Modelo GEE
En la que:
Yit Es la variable de resultado para el sujeto i en el tiempo t
i Es el sujeto
t Es el tiempo
β0 Es el intercepto
β1 Es el coeficiente de regresión para el tiempo
β2j Es el coeficiente de regresión para la variable independiente j
Xijt Es la variable independiente j para el sujeto i en el tiempo t
J Es el número de variables independientes que cambian en el tiempo
β3m Es el coeficiente de regresión para la variable independiente m
Xim Es la variable independiente fija en el tiempo m para el sujeto i
M Es el número de variables independientes que no cambian en el tiempo (fijas)εit Es el error del sujeto i en el tiempo t
corr Es la estructura de correlación de trabajo
Modelo de efectos mixtos
La nomenclatura utilizada en el modelo de efectos mixtos corresponde a la misma explicada en el modelo marginal, solo con la adición del concepto aleatorio, representada como sigue:
β0i Es el intercepto aleatorio
β1it Es el coeficiente de regresión aleatorio para el tiempo
β2ij Es el coeficiente de regresión aleatorio para la covariable dependiente del tiempo
MODELOS DE TRANSICIÓN
Los modelos de Markov incluyen el concepto de estados o clasificaciones, que pueden ser exhaustivos (todos los estados posibles) y excluyentes (un individuo no puede estar en más de un estado en el mismo momento de tiempo). Adicionalmente, estos estados también pueden clasificarse en absorbentes y no absorbentes: el primer tipo implica el no abandono o la probabilidad cero de salir (ejemplo: muerte), y el segundo, la posibilidad de cambiar de un estado a otro (ejemplo: sano/enfermo). Los acontecimientos ocurren como pasos de un estado a otro, pasos que se producen en períodos uniformes de tiempo conocidos como ciclos y con una probabilidad de cambio que depende del estado en el que se encuentre el individuo en cada momento (21-23). Las particularidades que deben cumplir los modelos de Markov para poder utilizarse se resumen principalmente en que a un individuo solo se le permiten ciertos cambios entre los estados, los ciclos de duración deben ser constantes a lo largo del tiempo, un individuo solo puede hacer un cambio en cada ciclo y todos los individuos están regidos por las mismas probabilidades de cambio (21).
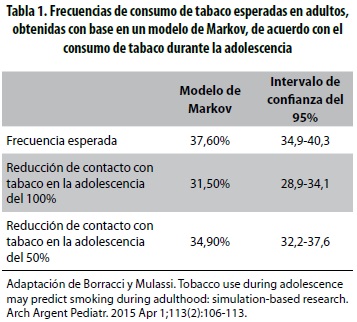
Borracci y Mulassi (24) desarrollaron una simulación con información de 421 adolescentes y 386 adultos con edades promedio de 14,3 (DE = 1,06) y 43,2 (DE = 10,6) años, respectivamente, con el objetivo de evaluar mediante un modelo de Markov si la influencia del consumo de tabaco durante la adolescencia podría predecir la prevalencia de tabaquismo en la edad adulta. Para esto obtuvieron las frecuencias de consumo de tabaco esperadas en adultos, para ser comparadas con las frecuencias de consumo observadas en una muestra de validación conformada por 1.218 adultos. La construcción del modelo demostró que fumar al menos un cigarrillo por mes durante la adolescencia era suficiente para predecir la frecuencia de consumo de tabaco en la edad adulta; además, que eliminar el consumo de tabaco durante la adolescencia puede reducir la frecuencia de consumo de tabaco en la edad adulta entre 12,2% y 16,2%. La simulación en el modelo con dos escenarios diferentes para la reducción absoluta del 50% y 100% del consumo de tabaco en la adolescencia, mostró reducciones relativas del consumo de tabaco del 7,2% y 16,2%, respectivamente, para fumadores adultos (tabla 1).
MODELOS MARGINALES
Liang y Zeger (19) presentaron en 1986 una generalización de las ecuaciones de estimación para el análisis de medidas repetidas. En ella se tiene en cuenta la correlación intragrupo en la estimación de los parámetros de la regresión de un modelo y se supone que la distribución marginal de la variable de resultado pertenece a la familia exponencial. Dichas ecuaciones se conocen como Ecuaciones Estimables Generalizadas (GEE) e incorporan la asociación entre las observaciones correspondientes a un mismo individuo, resultando de esta manera más apropiadas para el análisis de datos longitudinales (25). Específicamente, permiten considerar la dependencia entre las observaciones de un mismo sujeto asumiendo a priori una cierta ''estructura de trabajo'' o correlación. Las posibles estructuras de trabajo son: intercambiable, estacionaria, autorregresiva y no estructurada; con la primera aparentemente adecuada para la gran mayoría de situaciones (4).
En 2013 se publicó la investigación Clinical course of sepsis, severe sepsis, and septic shock in a cohort of infected patients from ten Colombian hospitals (26), un subanálisis de La Epidemiología de la Sepsis en Colombia (2), donde se buscó establecer la evolución y los determinantes de la progresión de infección (infección sin sepsis, sepsis, sepsis grave y choque séptico) mediante un modelo de GEE. En el análisis univariado la mayoría de variables estudiadas incrementaban el riesgo de progresión a estados clínicos de mayor gravedad durante la primera semana de hospitalización. En el análisis ajustado, en cambio, solo las fuentes de infección respiratoria, abdominal y otras infecciones, al igual que los puntajes SOFA y APACHE II, se conservaron como determinantes de progresión durante la primera semana (tabla 2).
MODELOS DE EFECTOS MIXTOS
El modelo de efectos mixtos es el que permite modelar la variable dependiente en función de factores aleatorios individuales y variables independientes. Se entiende por factores aleatorios aquellos que agrupan o clasifican la población por efectos de probabilidad de ocurrencia, y dicha clasificación no está correlacionada o explicada por ninguna de las variables independientes del modelo (27).
En Medellín se llevó a cabo un ensayo clínico aleatorio para determinar el efecto de la heparina a bajas dosis y en infusión continua en el tiempo de estancia hospitalaria y el cambio en el puntaje de disfunción de órganos (MOD) durante el manejo hospitalario de pacientes con sepsis (28). El análisis realizado por medio de un modelo de efectos mixtos demostró que tanto el grupo de placebo como el grupo de heparina tuvieron una reducción diaria estadísticamente significativa en el puntaje MOD (-0,13; IC 95% = -0,159; -0,105 y -0,11; IC 95% = -0,137; - 0,080, respectivamente), pero la diferencia entre esas dos velocidades de declive no fue estadísticamente significativa (p = 0,24).
CONCLUSIONES
El ADL es una herramienta adecuada para construir indicadores de cambio y valoración de intervenciones en salud, al permitir el estudio más detallado de una característica que cambia en el tiempo. Además, se convierte en el método más apropiado para procesar, analizar y entender distintos fenómenos biológicos que son determinantes para establecer los procedimientos y las conductas terapéuticas óptimas para la atención en salud.
REFERENCIAS BIBLIOGRÁFICAS
1. Greenland S. Introduction to regresion modeling. In: Rothman KJ, Greenland S, editors. Modern Epidemiology. 2ª ed. Filadelfia: Lippincott-Raven; 1998. p. 359-432. [ Links ]
2. Rodríguez F, Barrera L, De La Rosa G, Dennis R, Dueñas C, Granados M, et al. The epidemiology of sepsis in Colombia: a prospective multicenter cohort study in ten university hospitals. Crit Care Med. 2011 Jul;39(7):1675-82. DOI 10.1097/CCM.0b013e318218a35e. [ Links ]
3. Montero Díaz M, Castells Gil E, Lantigua Maldonado I. Modelos multinivel: Una aplicación a datos longitudinales en una investigación médica. Investigación Operacional. 2007;28(2):170-8. [ Links ]
4. Twisk JWR. Applied longitudinal data. Analysis for Epidemiology: A practical guide. Cambridge: Cambridge University Press; 2003. [ Links ]
5. Homish GG, Edwards EP, Eiden RD, Leonard KE. Analyzing family data: A GEE approach for substance use researchers. Addict Behav. 2010 Jun;35(6):558-63. DOI 10.1016/j.addbeh.2010.01.002. [ Links ]
6. Cnaan A, Laird NM, Slasor P. Using the general linear mixed model to analyse unbalanced repeated measures and longitudinal data. Stat Med. 1997 Oct;16(20):2349-80. [ Links ]
7. Arnau J, Balluerka N. Análisis de datos longitudinales y de curvas de crecimiento. Enfoque clásico y propuestas actuales. Psicothema. 2004;16(1):156-62. [ Links ]
8. Rouanet H, Lépine D. Comparison between treatments in a repeated-measurement design: anova and multivariate methods. Br J Math Stat Psych. 1970 Nov;23(2):147-63. DOI 10.1111/j.2044-8317.1970.tb00440.x. [ Links ]
9. Arnau Gras J, Bono Cabré R. Estudios longitudinales: modelos de diseño y análisis. Escr Psicol. 2008;2(1):32-41. [ Links ]
10. Huynh H, Feldt LS. Conditions under which mean square ratios in repeated measurements designs have exact F-Distributions. J Am Stat Assoc. 1970;65(332):1582-9. DOI 10.1080/01621459.1970.10481187. [ Links ]
11. McCullagh P, Nelder JA. Log-linear models. In: Generalized Linear Models. 2ª ed. London: CRC; 1989. p. 193-236. DOI 10.1007/978-1-4899-3242-6. [ Links ]
12. Arnau-Gras J. Estudios longitudinales de medidas repetidas. Modelos de diseño y de análisis. Avances en medición. 2007;5:9-26. [ Links ]
13. Liang K, Zeger S, Qaqish B. Multivariate Regression Analyses for Categorical Data. J R Statist Soc B. 1992;54(1):3-40. [ Links ]
14. Diggle P, Heagerty P, Liang K, Zeger S. Analysis of Longitudinal Data. New York: Oxford University Press; 2001. [ Links ]
15. Fahrmeir L, Tutz G. Modelling and Analysis of Cross- Sectional Data: A Review of Univariate Generalized Linear Models. In: Multivariate statistical modelling based on generalized linear models. 2ª ed. New York: Springer; 2001. p. 15-67. [ Links ]
16. Molenberghs G, Verbeke G. Model Families. In: Models for discrete longitudinal data. New York: Springer; 2005. p. 45-52. [ Links ]
17. Neuhaus JM, Kalbfleisch JD, Hauck WW. A comparison of cluster-specific and population-averaged approaches for analyzing correlated binary data. Int Stat Rev. 1991;59(1):25-35. [ Links ]
18. Delgado Rodríguez M, Llorca Díaz J. Estudios longitudinales: conceptos y particularidades. Rev Esp Salud Pública. 2004 Mar-Abr;78(2):141-8. [ Links ]
19. Liang K, Zeger S. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73(1):13- 22. [ Links ] DOI 10.1093/biomet/73.1.13.
20. Twisk JW. Longitudinal data analysis. A comparison between generalized estimating equations and random coefficient analysis. Eur J Epidemiol. 2004;19(8):769-76. [ Links ]
21. Terrés R. Introducción a la utilización de los modelos de Markov en el análisis farmacoeconómico. Farm Hosp. 2000;24(4):241-7. [ Links ]
22. Beck JR, Pauker SG. The Markov process in medical prognosis. Med Decis Making. 1983;3(4):419-58. [ Links ]
23. Naimark D, Krahn MD, Naglie G, Redelmeier DA, Detsky AS. Primer on medical decision analysis: Part 5--Working with Markov processes. Med Decis Making. 1997 Apr-Jun;17(2):152-9. [ Links ]
24. Borracci RA, Mulassi AH. Tobacco use during adolescence may predict smoking during adulthood: simulation-based research. Arch Argent Pediatr. 2015 Apr;113(2):106-12. DOI 10.1590/S0325-00752015000200006. [ Links ]
25. Nores M, Díaz M. Construcción de modelos GEE para variables con distribución simétrica. Rev SAE. 2005;9:43-63. [ Links ]
26. León AL, Hoyos NA, Barrera LI, De La Rosa G, Dennis R, Dueñas C, et al. Clinical course of sepsis, severe sepsis, and septic shock in a cohort of infected patients from ten Colombian hospitals. BMC Infect Dis. 2013 Jul;13:345. DOI 10.1186/1471-2334-13-345. [ Links ]
27. Spiegel M, Schiller J, Srinivasan A. Análisis de la varianza. En: Probabilidad y Estadística. 2ª ed. México DF: McGraw-Hill; 2007. p. 335-71. [ Links ]
28. Jaimes F, De La Rosa G, Morales C, Fortich F, Arango C, Aguirre D, et al. Unfractioned heparin for treatment of sepsis: A randomized clinical trial (The HETRASE Study). Crit Care Med. 2009 Apr;37(4):1185-96. DOI 10.1097/CCM.0b013e31819c06bc. [ Links ]