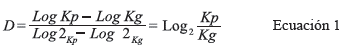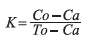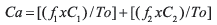Introducción
Predecir el comportamiento de un sistema a partir del cambio temporal de las variables dinámicas de éste, constituye el problema central de la teoría de los sistemas dinámicos1,2. Para el estudio de la dinámica de un sistema se utilizan representaciones gráficas en el espacio de fase, las cuales han sido denominadas atractores3, generalmente se encuentran dos tipos de atractores; los predecibles y los impredecibles, los primeros corresponden a dinámicas como la del péndulo o el sistema solar, mientras que los impredecibles llevan a atractores caóticos que pueden estudiarse con la geometría fractal.
La geometría fractal fue desarrollada por Benoit Mandelbrot y estudia los objetos irregulares de la naturaleza4-6, mientras que los objetos geométricos regulares son estudiados por la geometría euclidiana. Varios tipos de fractales se han definido; los salvajes, los matemáticos y los estadísticos, para cada uno de estos tipos se asocia un cálculo específico de la dimensión fractal. La dinámica cardiaca presenta un comportamiento caótico, por lo que su atractor corresponde a un fractal salvaje, que presenta superposición de sus partes, para calcular su dimensión fractal generalmente se utiliza el método de Box-counting7.
Se considera que las Enfermedades Cardiovasculares (ECV) son causadas por desórdenes cardiacos y de los vasos cardiacos, sus principales causas son el uso de tabaco, la inactividad física, dieta no saludable o el abuso de alcohol. De acuerdo a la Organización Mundial de la Salud (OMS)8, las ECV son la principal causa de muertes a nivel mundial; y se estima que cerca de 23.6 millones de personas morirán debido a éstas en 2030, principalmente por enfermedad cardiaca y accidente cerebrovascular, continuando así en el primer lugar de las causas de mortalidad. Solamente en E.E.U.U.9, las ECV cobran anualmente, más vidas que el cáncer y Chronic Lower Respiratory Disease (CLRD) juntos.
Uno de los exámenes diagnóstico más utilizados para identificar alteraciones significativas del ritmo cardiaco de característica transitoria, de presentación súbita y condiciones asintomáticas es el Holter10, este examen es una prueba de electrocardiografía ambulatoria, de tipo no invasivo, que evalúa 2 o 3 canales electrocardiográficos durante un período de 24 a 48 horas. Dentro de la evaluación convencional de la dinámica cardiaca, el análisis de la Variabilidad de la Frecuencia Cardiaca (VFC) a partir de los cambios del intervalo RR en el tiempo, ha sido uno de los mayores campos de interés en la cardiología actual, debido a que su variabilidad, particularmente cuando se encuentra disminuida, se asocia a eventos como muerte súbita arrítmica11, eventos cardiacos no arrítmicos como infarto agudo de miocardio12 y muerte por falla cardiaca13, además de eventos arrítmicos no fatales después de un infarto agudo de miocardio14.
Sin embargo, el análisis de la dinámica cardiaca y de la VFC desde teorías físicas y matemáticas ha controvertido muchos de los supuestos de la fisiología clásica e incluso la importancia de la VFC como predictor de eventos en la dinámica cardiaca, por ejemplo, a partir de la teoría de los sistemas dinámicos se ha desarrollado una reinterpretación del concepto de normalidad-enfermedad, en la que una dinámica cardiaca normal, lejos de comportarse de manera regular y cíclica como la fisiología clásica lo indica, se caracteriza por tener un comportamiento irregular e intermedio entre los dos extremos asociados a dinámicas patológicas que constituyen las dinámicas muy regulares o las extremadamente aleatorias15-19.
Con base en la metodología de evaluación hallada previamente20, la presente investigación busca analizar dinámicas cardiacas durante 18 horas con el fin de comprobar su capacidad de evaluación y su aplicabilidad clínica como ayuda diagnostica.
Materiales y Métodos
Definiciones
Atractor de frecuencias cardiacas: Mapa de retardo que se desarrolla a partir de graficar cada frecuencia cardiaca como función de la frecuencia cardiaca previa.
Dimensión Fractal de Box-Counting (D):
Donde Kp corresponde al número de cuadros ocupado por el objeto para la rejilla con partición 2 Kp y Kg corresponde al número de cuadros ocupado por el objeto para la rejilla con partición 2 Kg .
Ley exponencial de la dinámica cardiaca caótica: De la ecuación 1 se obtiene una relación exponencial entre los espacios ocupados y la dimensión fractal (D):
Población: Se tomaron en total 80 Holter o registros electrocardiográficos con una duración de mínimo 21 horas, de los cuales 15 correspondieron a casos diagnosticados por un cardiólogo experto como normales, y 65 casos correspondieron a casos diagnosticados con diferentes tipos de patologías pertenecientes a sujetos mayores de 21 años.
Procedimiento: De cada Holter o registros electrocardiográficos se tomaron los valores máximos y mínimos de las frecuencias cardiacas y el número total de latidos por hora, primero se tomó todo el registro y luego a partir de estos valores y de un programa previamente desarrollado (20) se generó una secuencia de las frecuencias cardiacas; estas fueron graficadas en el espacio de fases mediante un mapa de retardo (ver definiciones) en el cual se ubica una frecuencia cardíaca la una contra la siguiente en ambos ejes del mapa, construyendo de esta manera el atractor caótico de la dinámica cardiaca (Figura 1).
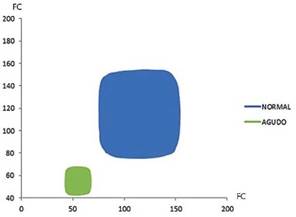
Figura 1 Atractores caóticos de la dinámica cardiaca. Ejemplos de dinámicas normal y aguda, correspondiente a los Holter 19 y 13, respectivamente (Tabla 1) FC: frecuencia cardíaca
Tabla 1 Medidas de los espacios de ocupación de los atractores calculados con datos del Holter durante 21 horas y 18 horas.
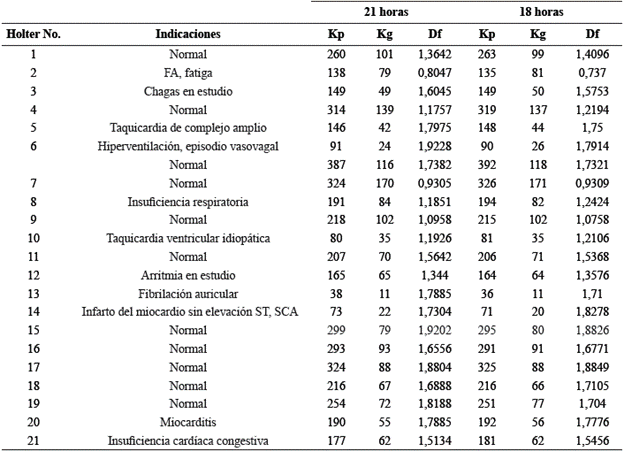
Kp: rejilla con cuadros pequeños.
Kg: rejilla con cuadros grandes.
Df: dimensión fractal.
Luego, se calculó la dimensión fractal por medio del método de Box-counting (ecuación 1) superponiendo dos rejillas (Kp y Kg) para cuantificar los espacios ocupados por cada atractor y se estableció la evaluación física y matemática establecida previamente. De manera que, un Holter asociado a enfermedad será aquel que para su atractor caótico, se hallaron espacios de ocupación Kp inferiores a 73. Mientras que una dinámica normal se estableció cuando se encuentren espacios de ocupación Kp mayores de 200. El estado de evolución hacia la enfermedad se determina cuando se encuentren espacios de ocupación que se encuentren entre 73 y 200.
Posteriormente se desarrolló el mismo proceso, pero con sólo 18 horas para cada Holter, y una vez obtenidas las medidas matemáticas se compararon con las obtenidas con la totalidad del registro, en busca de similitudes o diferencias. Luego se buscaron concordancias o divergencias al comparar el diagnóstico físico-matemático aplicado a 18 horas y el diagnóstico convencional.
Análisis estadístico: Para el análisis estadístico que compara la metodología matemática con el Gold estándar; fue necesario utilizar una clasificación binaria, hallando Verdaderos Positivos (VP), Verdaderos Negativos (VN), Falsos Positivos (FP) y Falsos Negativos (FN) para calcular sensibilidad y especificidad, siendo cada uno de ellos:
VP = casos evaluados convencionalmente y matemáticamente como patológicos,
VN = casos evaluados convencionalmente y matemáticamente como normales,
FP = casos evaluados convencionalmente como normales, pero que presentaron valores matemáticos de enfermedad,
FN = casos evaluados convencionalmente como enfermos, pero que presentaron valores matemáticos de normalidad.
También se evaluó la concordancia entre el diagnóstico convencional y el físico-matemático por medio de la ecuación del coeficiente Kappa:
Donde, Co representa el número de concordancias observadas entre el diagnóstico matemático y el Gold estándar; To es el número total de casos; Ca corresponde al número de concordancias atribuibles al azar que se calculan a través de la siguiente ecuación:
Donde
f1 = número de Holter con valores matemáticos de normalidad,
f2 = número de casos evaluados matemáticamente como enfermedad,
C1 = número de casos diagnosticados como normales por el experto clínico,
C2 = número de casos diagnosticados desde el ámbito clínico convencional con alguna patología
Consideraciones éticas
De acuerdo con la Resolución 8430 de 1993 del Ministerio de Salud colombiano, esta investigación presenta riesgo mínimo, pues los cálculos son realizados sobre bases de datos de reportes de exámenes que han sido prescritos previamente según protocolos establecidos convencionalmente. También se ha protegido el anonimato e integridad de los participantes, como lo reglamenta dicha resolución, así como la Declaración de Helsinki de la Asociación Médica Mundial.
Resultados
Al evaluar la totalidad del registro, se encontró que para la rejilla Kp, los espacios de ocupación estuvieron entre 37 y 389, y para la rejilla Kg estuvieron entre 11 y 172, las dimensiones fractales estuvieron entre 0,7897 y 1,9234.
Los Holter clasificados como normales presentaron valores de ocupación Kp mayores a 200 tanto para 21 como para 18 horas, lo que corresponde a una evaluación matemática de normalidad, y para la evaluación en 18 horas de los casos de Holter agudos se tuvieron valores de Kp menores a 73, siendo consistentes con lo encontrado previamente para 21 horas o más20.
El coeficiente Kappa fue de 1 y los valores de sensibilidad y especificidad fueron del 100%, la evaluación matemática realizada por la metodología diferencia normalidad de enfermedad aguda, así mismo caracteriza numéricamente los casos que se encuentran evolucionando entre normalidad y enfermedad aguda. Al comparar las evaluaciones realizadas para 21 y 18 horas, se observa que las medidas son consistentes, evidenciando que la metodología es aplicable en 18 horas.
Discusión
La ley de la dinámica caótica cardiaca exponencial permitió deducir la totalidad de posibles atractores cardiacos; la dinámica cardiaca presenta un comportamiento caótico, y la representación gráfica de dicha dinámica presenta una forma irregular que puede ser caracterizada con la geometría fractal, esta geometría ha sido aplicada en diferentes ámbitos de la medicina21-25 buscando diferenciar normalidad de enfermedad, sin embargo, las dimensiones fractales aisladas han mostrado no ser concluyentes para lograr esta diferenciación26,27, por esto se han desarrollado diferentes conceptos para lograr dicha diferenciación28,29. De igual forma, en la dinámica cardiaca, las dimensiones fractales aisladas han mostrado ser insuficientes para diferenciar normalidad y enfermedad20,30,31, siendo los espacios de ocupación del atractor, lo que permite establecer un diagnóstico para cada caso particular, independientemente de metodologías estadísticas y epidemiológicas que describen comportamientos poblacionales.
A partir de métodos lineales, la teoría del caos y el análisis fractal se han desarrollado nuevas metodologías para el estudio de las dinámicas fisiológicas32-38, con esto se han logrado contribuciones importantes, entre ellas, una nueva concepción de normalidad enfermedad15, así como mejores predictores de mortalidad, y nuevos índices para cuantificar la complejidad de las dinámicas estudiadas, sin embargo es necesario realizar más estudios para establecer su aplicabilidad clínica39,40.
El máximo nivel de concordancia (coeficiente Kappa) entre el diagnóstico físico matemático y el Gold estándar fue obtenido, de igual forma la sensibilidad y especificidad fue del 100% mostrando así que la metodología fue capaz de diferenciar objetiva y cuantitativamente normalidad de enfermedad, permitiendo reducir el tiempo de evaluación de la dinámica cardiaca, lo que podría ser de ayuda en la rapidez con la que el paciente sea evaluado, contribuyendo a mejorar la atención de éste.
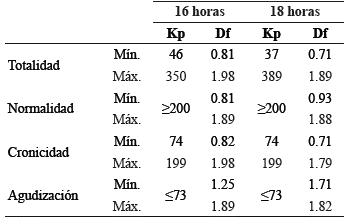
A partir de lo anterior, es posible concluir que la metodología caótica matemática puede discriminar el estado de la dinámica cardíaca, diferenciando la normalidad de la enfermedad crónica de la aguda mediante la cuantificación los espacios de ocupación de los atractores y que ésta soporta una reducción del tiempo de evaluación a 18 horas manteniendo su misma capacidad diagnóstica. La reducción del tiempo de evaluación ha sido evaluada anteriormente en otros estudio a 16 horas1, cuyos valores son comparados con los obtenidos en esta investigación (Tabla 2), confirmando que los valores de la dimensión fractal no permiten obtener diferencias entre ningún estado, mientras que los espacios de ocupación de la rejilla Kp si lo permiten en el 100% de los casos, con lo cual se ratifica la capacidad diagnóstica de la metodología implementada.
Tabla 2 Comparación de los resultados obtenidos de la dimensión fractal y la rejilla Kp en 16 y 18 horas.
Esta metodología, tanto a 18 como a 16 horas, podría indicarse en la práctica clínica cotidiana para realizar el seguimiento de pacientes en las Unidades de Cuidados Intensivos (UCI) en el contexto de enfermedades agudas como las patologías isquémicas cardiacas o en el postoperatorio, como en la cirugía cardiovascular, ya que mostraría la evolución de la dinámica en el tiempo y le indicaría a los clínicos si las intervenciones realizadas han tenido éxito o si existe algún deterioro, sin tener que lidiar con factores subjetivos de interpretación al ser una medida netamente cuantitativa, siendo más útil con mayores reducciones de horas de evaluación.
También se indicaría en los pacientes ambulatorios a quienes se haya indicado un estudio Holter por cualquier razón ya que resulta útil evaluar la evolución de la dinámica cardíaca en la consulta externa para realizar el seguimiento de pacientes con enfermedades crónicas como las arritmias cardíacas. Sin embargo, deben realizarse estudios con distintos escenarios clínicos y distintas horas de registro para confirmar los hallazgos experimentales. Su mayor utilidad resultará de su automatización para proveer información útil y objetiva a los clínicos.
En otros ámbitos de la medicina se ha logrado llegar a generalizaciones que permiten establecer predicciones de un fenómeno específico como en el campo de la la epidemiología42, la morfometría28,29 y la infectología43. En el campo de la biología molecular y la inmunología, se desarrolló una teoría que permite la predicción del fenómeno de unión de péptidos al HLA clase 2 desde la probabilidad y la entropía44, y de igual forma en el campo de la cardiología45. También se han desarrollado predicciones en la UCI46 de mortalidad mediante la teoría de conjuntos aplicada a atractores de variables hemodinámicas.