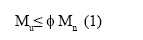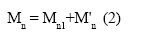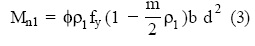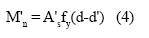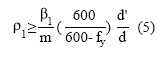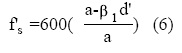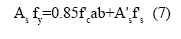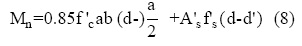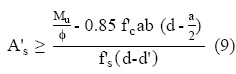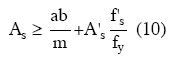Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Facultad de Ingeniería
Print version ISSN 0121-1129
Rev. Fac. ing. vol.24 no.40 Tunja Sept./Dec. 2015
Método de la deformación unitaria para diseño de vigas rectangulares doblemente reforzadas
Strain method for doubly reinforced rectangular beams design
Método da deformação unitária para desenho de vigas retangulares duplamente reforçadas
Luis Rafael Prieto-Serrano*
* M.Sc. Universidad Pedagógica y Tecnológica de Colombia (Tunja-Boyacá, Colombia). luis.prieto@uptc.edu.co.
Cómo citar este artículo: [1] L. R. Prieto-Serrano, "Método de la deformación unitaria para diseño de vigas rectangulares doblemente reforzadas", Fac. Ing., vol. 24 (40), pp. 31-40, Sep.-Dic. 2015.
Fecha de Recepción: 03 de noviembre de 2014 Fecha de Aceptación: 12 de julio de 2015
Resumen
El acero en compresión en una viga doblemente reforzada mejora la ductilidad, reduce las deflexiones instantáneas y de largo plazo, está disponible para tomar la tracción en secciones sometidas a reversión de esfuerzos y, en vigas de poca altura, aumenta la resistencia. A partir de la deformación unitaria esperada del acero en tracción, como medida de la ductilidad de la sección, se propone una metodología directa para determinar las cantidades de refuerzo necesarias, tanto en compresión como en tracción. Se establece que las secciones más eficientes son aquellas para las cuales la deformación en el acero en tracción es 0.005.
Palabras clave: Concreto estructural, Diseño de vigas, Deformación unitaria, Ductilidad, Viga doblemente reforzada.
Abstract
The compressed steel in a doubly reinforced beam improves ductility, reduces immediate and long-term deflections, it is available to support the tension in sections under reversal stress, and in low-height beams, it increases strength. With the expected strain as a measure of the section ductility, the paper proposes a direct methodology to determine the necessary compression quantities and tension reinforcement. It finds that the most efficient sections are those for which the tension reinforcing strain is 0.005.
Key Words: Beams design, Doubly Reinforced Beam, Ductility, Strain, Structural Concrete.
Resumo
O aço em compressão em uma viga duplamente reforçada melhora a ductilidade, reduz as deflexões instantâneas e de longo prazo, está disponível para tomar a tração em seções submetidas a reversão de esforços e, em vigas de pouca altura, aumenta a resistência. A partir da deformação unitária esperada do aço em tração, como medida da ductilidade da seção, propõe-se uma metodologia direta para determinar as quantidades de reforço necessárias, tanto em compressão como em tração. Estabelece-se que as seções mais eficientes são aquelas para as quais a deformação no aço em tração é de 0.005.
Palavras chave: Concreto estrutural, Desenho de vigas, Deformação unitária, Ductilidade, Viga duplamente reforçada.
I. Introducción
En la primera edición de este siglo del Reglamento ACI 318 [1] se introdujeron modificaciones importantes en los factores de carga de las combinaciones de carga y en los factores de reducción de resistencia φ utilizados en diseño; estos cambios fueron adoptados integralmente por el NSR-10 [2], que reemplazó las NSR-98 [3] y reformó la práctica de diseño de vigas en Colombia.
El factor de reducción de resistencia φ contemplaba variaciones en la resistencia de los materiales y en las dimensiones de las secciones, defectos en la colocación del acero de refuerzo y aproximaciones en las hipótesis de diseño, y dependía de la importancia de la fuerza interna en cuanto a la consecuencia de la falla de los elementos "respecto a toda la estructura y el grado de advertencia implícita en el modo de falla" [4]. La práctica actual, además, contempla el grado de ductilidad de la sección, por lo que ahora φ se determina "por las condiciones de deformación unitaria en las secciones transversales" [5].
Los cambios en la conceptualización del factor de reducción de resistencia permiten apartarse del control de cuantías del acero, necesarios en la práctica anterior, y concentrarse en la deformación unitaria del acero de refuerzo a tracción, como una medida más directamente relacionada con la ductilidad de las secciones de concreto reforzado.
Con un procedimiento como el que aquí se propone para vigas rectangulares de concreto estructural doblemente reforzadas se determinan directamente las cantidades de acero necesarias en compresión y en tracción.
II. El problema de diseño
El diseño estructural tiene como uno de sus objetivos proveer elementos dúctiles, con el fin de desarrollar una buena capacidad de disipación de energía; hoy en día, para cumplir con este propósito se debe garantizar que cuando se alcance la resistencia de la viga en la sección crítica, el acero longitudinal extremo en tracción debe presentar mínimo una deformación unitaria εt de 0.004 [2, 5].
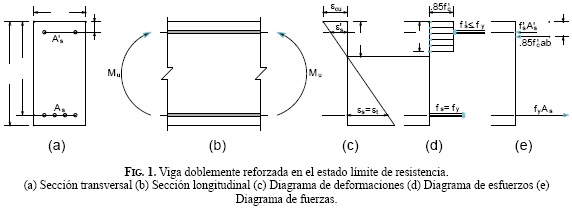
Para una sección rectangular de concreto doblemente reforzada por As y A's (Fig. 1.a) sometida a la acción de un momento flector mayorado de diseño Mu (Fig. 1.b) se define la altura efectiva d como "la distancia desde la fibra extrema en compresión hasta el centroide del refuerzo longitudinal en tracción" [2], y, similarmente, d’ como "la distancia desde la fibra extrema en compresión hasta el centroide del refuerzo longitudinal en compresión" [2]. En la práctica de diseño de vigas de concreto estructural estas alturas se aproximan al centímetro [2, 5].
Teniendo presentes las suposiciones de diseño de elementos de concreto reforzado, ampliamente documentadas [4, 6, 7]:
- Se parte de la hipótesis de deformación de Bernoulli-Euler, mediante la cual secciones planas antes de la flexión permanecen planas después de ella (Fig. 1.c). Esto permite establecer c, la frontera entre las fibras en tracción y las de compresión.
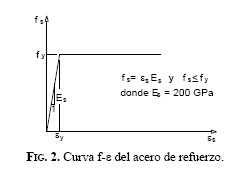
- No se considera la zona de endurecimiento por deformación del acero de refuerzo, al definir su comportamiento, en tracción y en compresión, con una curva f-ε perfectamente elastoplástica (Fig. 2).
- Se desprecia la contribución del concreto para resistir tracciones.
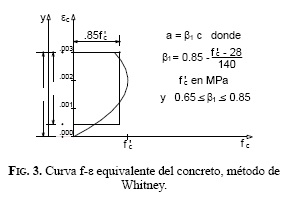
- Para evaluar la resistencia del concreto en compresión se utiliza el método de Whitney [8] en reemplazo de la "forma general de la curva f-ε del concreto" [5] (ver Fig. 3 con ejes intercambiados), que facilita el diseño sin modificar la sensibilidad de la magnitud de la resistencia. β1 es un factor de forma "que relaciona la profundidad del bloque rectangular equivalente de esfuerzos con la profundidad del eje neutro" [2].
- Mediante pruebas de laboratorio se ha demostrado que la resistencia de la sección se alcanza cuando falla el concreto, haya fluido o no el acero a tracción [4, 6, 7]. Para efectos de diseño se ha establecido que la falla del concreto se presenta cuando la fibra extrema alcanza una deformación e cu de 0.003 [2], y el acero a tracción fluye.
Al momento de alcanzarse la resistencia, el diagrama de esfuerzos en la sección crítica de la viga corresponderá al que se observa en la Fig. 1.d.
Integrando cada uno de estos esfuerzos en las respectivas áreas en que actúan, las fuerzas obtenidas se muestran en la Fig. 1.e. La resultante de estas fuerzas será un par Mn, momento nominal resistente, que en diseño debe ser tal que:
donde Φ es el factor de reducción de resistencia, que toma en cuenta variaciones en las calidades de los materiales y en la mano de obra, en cuanto dimensiones de la sección y colocación del acero de refuerzo y el tipo de falla que se puede llegar a presentar en el elemento y su importancia en la estructura [5]. En la práctica actual de diseño Φ depende de la deformación unitaria del acero de refuerzo extremo en tracción et [2, 5].
III. Resistencia nominal resistente de secciones dúctiles doblemente reforzadas
Para que una sección de concreto reforzado sometida a flexión sea dúctil es necesario que el acero de refuerzo a tracción se deforme de tal manera que esté trabajando en el rango plástico al alcanzar el estado límite de resistencia. Así, la deformación unitaria del acero a tracción debe ser ε s >ε y, por lo que la sección, al alcanzar la resistencia, se garantiza que el esfuerzo en el acero a tracción es el límite de fluencia f y (Fig. 1.d). De otro lado, el acero a compresión puede haber fluido o no.
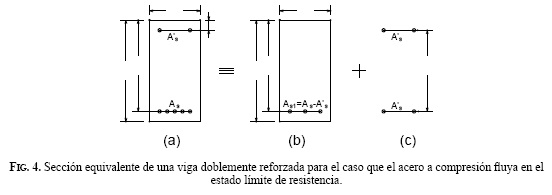
Si en el estado límite de resistencia tanto el acero a tracción como el de compresión fluyen, al determinar el momento nominal resistente Mn es usual considerar la sección doblemente reforzada As1=A sl -A's (Fig. 4.a) como el equivalente a la sección reforzada con una cantidad de acero a tracción igual a (Fig. 4.b) más la acción de la cantidad de acero en compresión A's actuando tanto en las fibras superiores como inferiores (Fig. 4.c). Así, la resistencia nominal de la sección se puede evaluar como:
en el que Mn1 es el momento nominal resistente de la sección simplemente reforzada con AS1:
donde ρ1 es la cuantía de la sección simplemente reforzada (As1 ⁄ bd ) y m la relación de resistencias de los materiales constitutivos de la viga: fy ⁄ 0.85f'c .
Similarmente, M'n corresponderá al momento del par de fuerzas que se presentan en el refuerzo A's tanto en las fibras superiores como inferiores:
Se demuestra que el acero en compresión fluye cuando la cuantía ρ1 es
Si la desigualdad (5) no se cumple, el acero en compresión no fluye, lo que se presenta en el apartado B.
B. Caso II. En el límite de resistencia, el acero a compresión no fluye.
En secciones dúctiles doblemente reforzadas - aquellas que en la resistencia el acero a tracción alcanza la fluencia- para las que el acero a compresión no fluye, es decir, pueden establecer dos ecuaciones del esfuerzo del acero en compresión en función de la profundidad del bloque rectangular equivalente de esfuerzos del concreto. Una de ellas a partir del diagrama de deformaciones (Fig. 1.c),
y la otra del equilibrio de fuerzas axiales (Fig. 1.e):
Reemplazando la ecuación (6) en (7), da como resultado un polinomio de segundo grado en función de a, que sería la única incógnita. Así, el momento nominal resistente será:
IV. Expresiones para diseño
La deformación del concreto ε cu ha sido fijada en el diagrama de deformaciones (Fig. 1.c) para el estado límite de la resistencia en 0.003. Se observa que no solo la posición del eje neutro c, sino también la deformación unitaria al centroide del acero en compresión ε’s, dependen del valor de εs (la deformación unitaria en el centroide del acero longitudinal del refuerzo en tracción) o de εt, que para este caso es igual. Conocida la deformación, se determina el esfuerzo por lo que en la condición crítica de diseño M u = Φ M n, del par resultante de las fuerzas que actúan en la sección (Fig. 1.e), se deduce que:
y del equilibrio de fuerzas
V. El diseño
Conociendo las dimensiones de la viga, en general resultantes de un análisis de rigidez de la estructura por diseñar, se especifica la resistencia del concreto f’c y el límite de fluencia del acero de refuerzo longitudinal f y, para que resista el momento mayorado crítico Mu resultante de las combinaciones de carga que puedan actuar durante su vida útil.
Como usualmente se hace, el diseño de secciones de concreto reforzado parte de suponer que la viga es simplemente reforzada, si la solución presenta una cuantía mayor que la permitida -y si no es conveniente o posible cambiar de dimensiones o si es poco práctico modificar especificaciones de materiales- existirá siempre la posibilidad de colocar acero en compresión.
El diseño de secciones rectangulares doblemente reforzadas -a partir del recubrimiento necesario y de estimar los diámetros del acero transversal y longitudinal- inicia por suponer la altura efectiva de la viga d y la posición del acero de refuerzo en compresión d’; de fijar un criterio de deformación unitaria del acero longitudinal extremo en tracción ety de que la cantidad de acero necesaria para reforzar la viga, tanto en tracción como en compresión, se pueda emplazar cada una en una fila de refuerzo.
Si esto último es factible, es la solución más económica. En este caso la posición del centroide del acero en tracción d será igual a dt, que es la "distancia desde la fibra extrema en compresión al centroide de la fila extrema de acero longitudinal en tracción" [2, 5]. De esta manera, εs = εt, lo que permite determinar todos los valores de las expresiones para diseño del punto anterior de una manera directa, incluidas las áreas de refuerzo necesarias en compresión y en tracción.
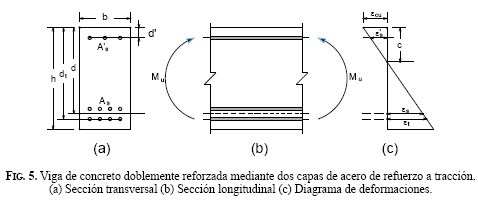
Si, por el contrario, el área de acero necesaria en tracción solo es posible colocarla en dos o más filas d<dt y εs <εt (Fig.5), con base en la Fig.5.c es posible determinar la posición del eje neutro para esta condición.
Como las áreas de refuerzo en diseño no se pueden colocar 'exactamente' al definir el número y diámetro de las barras a usar, se recomienda elegirlas ligeramente mayores que los valores determinados para As y A's, teniendo especial cuidado para que ΔA's >ΔA s, con el de las barras a usar, se recomienda elegirlas ligeramente fin de que εt sea mayor o similar al valor previsto de diseño.
Las expresiones de diseño (9) y (10) no toman en cuenta el área de concreto desplazada por el refuerzo en compresión; aunque sería más ‘exacto’, considerarla no cambia significativamente el momento resistente de la sección. Esto último es más cierto en la medida en que εt ≤ 0.005, y el momento resistente esté cercano al que puede resistir la viga con el máximo refuerzo permitido para la sección simplemente reforzada, donde la cantidad de acero en compresión es relativamente pequeña. En caso de que se aleje de estas condiciones y se considere necesario tomar en cuenta el área de concreto desplazada por el acero en compresión, el área de acero en compresión aumentaría y la de tracción permanecería constante.
Para los casos (excepcionales) que f's ≤ 0 la altura de la sección será insuficiente para las condiciones de diseño y, en la medida que este esfuerzo sea pequeño (εt ≫ 0.005 y Mu elevado), la sección tenderá a ser ineficiente, pues demandará grandes cantidades de acero.
VI. Eficiencia de la sección
El diseño debe definir la deformación unitaria que se espera que presente la fila extrema del acero de refuerzo en tracción de la viga en el estado límite de resistencia, la cual es una medida de la ductilidad de la sección e, indirectamente, de la capacidad de disipación de energía de la sección, "el límite de 0.005 proporciona un comportamiento dúctil para la mayoría de los diseños" [5]. En casos especiales, como en aquellos sitios donde se permita la redistribución de momentos εt, como mínimo debe ser 0.0075 [2, 5].
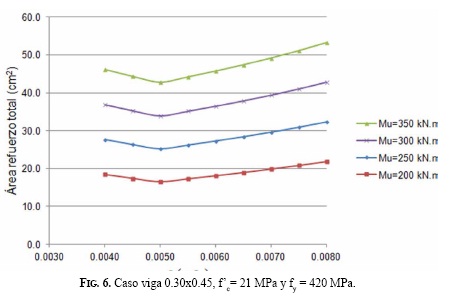
Para el caso de diseño de una viga de dimensiones constantes (0.30x0.45 m) y materiales conocidos (f’c = 21 MPa y fy = 420 MPa), el área de refuerzo total -la de tracción más la de compresión- necesaria para resistir un momento mayorado dado varía sensiblemente con la deformación unitaria requerida del acero longitudinal extremo de tracción εt. En la Fig. 6 se puede observar el área total teórica requerida para algunos momentos mayorados de diseño en función de εt. En todos los casos, la menor cantidad de acero total que necesita la sección se presenta cuando εt= 0.005.
Para valores entre 0.004 ≤ εt< 0.005, las cantidades de acero totales son mayores que para deformaciones unitarias de 0.005, debido al factor de reducción de resistencia φ que modifica al momento nominal resistente y que, a partir del ACI 318-02 [7], es función de εt y lo disminuye tan sensiblemente, por lo que en algunos casos demanda áreas totales superiores al 10% para deformaciones al límite de 0.004. Por esta razón, no existe justificación alguna-de comportamiento o económica- para diseñar secciones en este rango de deformaciones unitarias para el acero a tracción.
Por otro lado, si las deformaciones unitarias en el acero longitudinal extremo εt> 0.005, las áreas totales necesarias pueden ser mucho mayor es. Los casos mostrados pueden bordear el 30%, con εt = 0.0075, si Mu es cercano al que puede resistir la viga con el máximo refuerzo permitido para la sección simplemente reforzada. En la medida que los momentos sean mayores, estas proporciones de acero total van disminuyendo, aunque, como se mencionó, para todos los casos las secciones más económicas son aquellas para las cuales εt = 0.005, pues la necesidad de proveer mayor ductilidad de la sección demandará mayores cantidades de acero tanto en compresión como en tracción.
VII. Ejemplo
Una viga rectangular apoyada, simplemente, de 5.50 m de luz debe soportar una carga viva de servicio de 36.0 kN/m, además de una carga permanente de 15.3 kN/m. Por razones arquitectónicas, la sección transversal está limitada a un ancho de 0.25 m y a una altura de 0.50 m. Si el acero de refuerzo por usar tiene un límite de fluencia de 420 MPa, y el concreto, una resistencia especificada de 28 MPa, ¿cuál es el área (o áreas) de acero que debe(n) suministrarse?
La carga mayor a da de diseño es 1.2*15.3+1.6*36.0=76.0 kN/m.
Así, Mu= 76.0*5.502⁄8 =287 kN∙m. Para garantizar los requisitos de recubrimiento y espaciamiento del refuerzo a tracción se supone que su centroide está a 90 mm por encima de la cara inferior de la viga; de esta forma, d=0.41 m; se prevé que el centroide del acero de refuerzo extremo está a 70 mm de la cara inferior y dt=0.43 m. Para las calidades de acero y concreto de diseño, m=17.6. Si la viga fuese simplemente reforzada, la cuantía necesaria sería:

mayor que 0.0181*0.43/0.41=0.0190 -cuantía que corresponde a una εt=0.005-, lo que significa que es necesario reforzar la viga a compresión. Para este caso, con una deformación unitaria del acero extremo en tracción de 0.005, la altura de esfuerzos constantes en el concreto será:
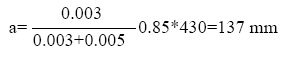
Si el centroide del acero a compresión está ubicado a 60 mm por debajo de la cara superior de la viga ( m), el esfuerzo al que estará sometido este acero valdrá (6):
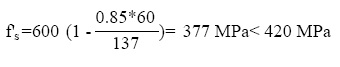
De la ecuación 9
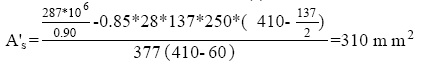
y de (10),
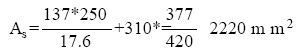
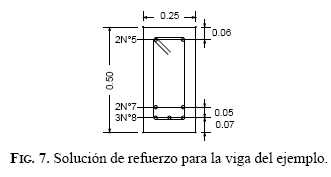
Se usan 3N°8 y 2N°7 con un área de 2300 mm2 para el acero de refuerzo a tracción dispuestos de la forma como se observa en la Fig.7, se verifica d y se determina r=0.0224. Como refuerzo a compresión se emplean 2N°5 con un área de 400 mm2 y un ρ'=0.0039.
Se verifica que el refuerzo colocado a la viga es suficiente para resistir el momento de diseño. ρ-ρ'=0.0185. Como es menor que (5):
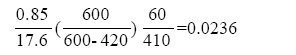
el acero a compresión no fluye al momento que la viga alcance la resistencia. Para este caso, al determinar ‘exactamente’ la altura del bloque de esfuerzos en el concreto al resolver el polinomio de segundo grado,
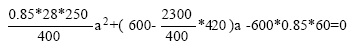
a=137 mm y con este, como se determinó anteriormente, f's=377MPa. Se verifica así que
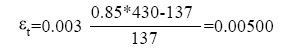
Por lo que y de (8):
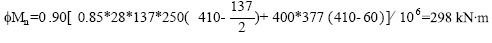
algo mayor que 287 kN∙m.
VIII. Conclusiones
El método de la deformación unitaria propuesto, para el diseño de vigas rectangulares de concreto estructural doblemente reforzadas, permite determinar las cantidades de acero de refuerzo en compresión y en tracción mediante un procedimiento directo.
Se determinó que en el diseño de vigas reforzadas a compresión, la deformación unitaria óptima que presente el acero de refuerzo extrema en tracción en el estado límite de resistencia es de 0.005. En casos especiales, como en aquellos sitios donde se permita la redistribución de momentos, para los cuales sea necesario garantizar una et mínimo de 0.0075, la demanda de acero aumenta sensiblemente, cercana al 30% mayor respecto de la necesaria para una deformación unitaria de 0.005.
Considerar secciones en el límite de resistencia con deformaciones unitarias menores a 0.005 es inconveniente debido a la reducción que se presenta en la ductilidad de la sección. La normatividad existente toma en consideración este comportamiento, disminuyendo el factor de reducción de resistencia φ, lo que se refleja en mayores demandas de refuerzo, afectando su viabilidad económica.
Referencias
[1] Committee ACI 318-American Concrete Institute, Building Code Requirements for Structural Concrete (ACI 318-02) and Commentary (ACI 318R-02), Farmington Hills, Michigan, American Concrete Institute, 2002, pp. 85-118. [ Links ]
[2] Asociación Colombiana de Ingeniería Sísmica, "Título C - Concreto estructural". En Reglamento Colombiano de Construcción Sismo Resistente - NSR-10, Bogotá, Colombia, Asociación Colombiana de Ingeniería Sísmica, 2010, pp. C1-C227. [ Links ]
[3] Asociación Colombiana de Ingeniería Sísmica, "Título C - Concreto estructural". En Normas Colombianas de Diseño y Construcción Sismo- Resistente - NSR-98, Bogotá, Colombia, Asociación Colombiana de Ingeniería Sísmica,1998, pp. C1-C588. [ Links ]
[4] R. Park, T. Paulay, Estructuras de concreto reforzado, Tr. S. Fernández, México D.F., México: Limusa S. A., 1983. [ Links ]
[5] Comité ACI 318-American Concrete Institute, Requisitos de Reglamento para Concreto Estructural (ACI 318S-11) y Comentario, Tr. Subcomité 318-S - American Concrete Institute, Farmington Hills, Michigan, American Concrete Institute, 2011. [ Links ]
[6] A. Nilson, D. Darwin, C. Dolan, Design of concrete structures, McGraw-Hill, 2010. [ Links ]
[7] O. González, O. Robles, Aspectos fundamentales del concreto reforzado, México D.F., México: Limusa S. A., 2005. [ Links ]
[8] C. S. Whitney, "Design of reinforced concrete members under flexure or combined flexure and direct compression", J. ACI, vol. 33, pp. 483- 498, Mar.-Apr. 1937. [ Links ]