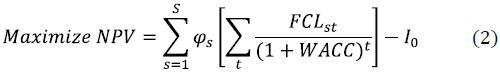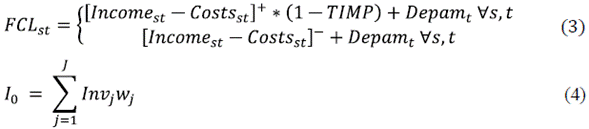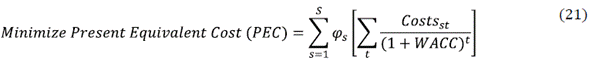I. Introduction
Logistics is responsible for planning, implementing, and controlling in an efficient and effective way the normal and reverse flow in the supply chain. Similarly, it handles warehousing, provides services, and supplies the information related to the different echelons in the chain to satisfy customers' demand. This administration process of the network encompasses three decision levels, according to the time horizon: strategic, tactical, and operational [1]. Strategic decisions, which usually have a horizon longer than a year, take into account the suppliers' selection, the facilities' optimal location, the type of products that will be manufactured, and the outsourcing of operations. Tactical decisions, which have a horizon shorter than a year, consider decisions such as selection of demand prediction techniques, administration and control of inventories, determination of production, storage and distribution policies, and selection of transportation modes, among others. Finally, operational decisions, whose time horizon is one week, days, or hours, involve resources planning, allocation of collecting processes (picking), and distribution and planning of routes, among others [1].
This paper addresses the distribution network design problem, considering tactical and strategical decisions such as the opening of distribution centers, and the establishment of product flows throughout the network with different demand scenarios. According to [1], the strategic and tactical decisions of the network design are usually hard to revert, and involve important investments of time and money. These decisions become more complex in environments where the network parameters are highly uncertain; therefore, what today may be an "optimal" network design in terms of optimization of an objective function, could be a "bad decision" in the future due to drastic changes in the parameters. Consequently, current decision models must represent the variability of the network critical parameters [1].
Theoretical and practical background on design decisions of a supply network, such as location, and allocation and consolidation of plants and distribution centers, date back to the early XX Century. However, current dramatic changes of international trade agreements have made the world the "target market", forcing the companies to be more flexible in the decisions about distribution network design.
In this sense, similar issues, such as the selection of the "optimal" location for new facilities, or the evaluation of the current facilities' location to either close them definitely or relocate them, have become decisions that must involve a specialized financial analysis. Traditionally, approaches on network design have focused on cost minimization, overlooking the financial aspect of the issue [2]. Therefore, this paper aims at addressing the problematic from a financial perspective, related with the maximization of the investment's Net Present Value (NPV) by means of optimization based on scenarios proposed in [1] and [3]. This methodology seeks to simultaneously optimize all the scenarios by formulating a mixed-integer linear programming model [3]. The results were compared with the traditional distribution network scheme of present value of cost minimization.
The problem addressed here consists of a three-echelon distribution system (plants, distribution centers, and clients), in which decisions about the opening of distribution centers must be made. The main contribution of this paper is the consideration of financial criteria to evaluate the distribution network design, and the application of an efficient optimization methodology that is based on scenarios with stochastic demand parameters. Likewise, this paper seeks to extend the literature in terms of applicability of the solution scheme proposed for a real case taken from a multinational food company that supplies the Colombian and some South and Central American markets. Papers considering solutions to distribution network redesign that use financial criteria, include demand variability, and apply the optimization methodology based on scenarios, are scarce in the literature.
This paper is structured as follows: Section 2 reviews the literature on supply network design with financial criteria and stochastic elements; Section 3 formulates the mathematical mixed-integer linear programming model, and the general structure of the proposed solution methodology; and finally, computational results, and conclusions are described in sections 4 and 5, respectively.
II. Literature review
The supply network design problematic is more critical nowadays, considering the effects of the diverse free trade agreements, the market's opening, and the access to product and reference diversification mechanisms.
Traditionally, the solution to the distribution network design problematic has been subjective, and solely based on the experience of the people in charge of the decision process, without considering formal elements or quantitative methodologies [4-7]. Clearly, any solution to the network design problem resulted from these methods will not offer any confidence to an organization; on the contrary, any mistake might deteriorate the organization's financial situation [1,6]. Decisions such as the location of a new plant or warehouse, or the relocation or definitive closure of a facility, may overflow the company's finances when the variables involved in such process are poorly known [7].
Currently, the economic changes that take place throughout the life cycle of a Company may drastically alter the supply network design; what today is an "optimal location for a plant or distribution center", tomorrow might be a "disastrous investment" [8]. The general idea of considering the problematic of facility location as an investment decision would mean that companies should obtain a return or profit from the money invested in such project. In this sense, the financial theory suggests that, to the extent that an investment is riskier, a higher return must be expected; that is, the expected profitability of any investment is proportionally linked to the inherent financial risk. Therefore, it is necessary to consider that any decision regarding distribution network design must be evaluated with financial criteria related with profitability, or the inherent risk of such decision or action. However, this does not happen in real life; many multinational companies neither analytically consider the financial risk nor the variability of the network critical parameters in the supply network optimization [8].
Despite the above mentioned, some studies have considered as objective the maximization of the financial value [9], or the minimization of the financial risk [10]. The risk in distribution network design has been addressed from several perspectives; a critical review of this topic has been proposed in [11]. In this work, different approaches for quantitative risk management of supply networks are addressed. Singhal et al. [12] used a multi-layer taxonomy to classify and codify the literature on supply network design, and finally, Klibi et al. [13] proposed a critical revision to the robust design of distribution networks.
You and Grossmann [14] tackled the supply network optimization, considering the sensitivity on decision criteria. They formulated the problem as a bi-objective optimization model, which seeks to maximize the NPV, and to minimize the expected transit time. A robust network design, contemplating the conflict between efficiency and risk was proposed in [15].
A multiobjective stochastic programing approach to design supply networks, considering risk, is proposed in [10]. Demand, supplier flows, processes, transportation, and expansion costs are regarded as probabilistic parameters. The multiobjective model considers the following objectives: i) minimization of logistics costs, ii) minimization of total cost variance, and iii) minimization of financial risk measured as the probability of not reaching the expected profit.
An applied case, related to the optimization of a bioethanol supply network under value uncertainty, is proposed in [16]; two optimization criteria are considered: risk seeking, and risk adversity. A study case of a Company in northern Italy is used to demonstrate the efficacy of the proposed mathematical model, which allows to maximize the economical profit, and to minimize the financial risk, identifying the best network topology in terms of location of crops and production sites, and distribution of products throughout the network [16].
On the other hand, part of the literature that contemplates uncertainty in the network design models has used, as a valid solution methodology, an approximation based on scenarios. In this methodology, the uncertainty in the network is represented by a discrete number of scenarios, and by considering random parameters [1,17]. According to [17], each scenario has an associated probability level, which represents the future state of a particular situation. The scenario based methodology seeks to find robust solutions that perform well in all scenarios [1], and stablish the construction of different discrete variables, according to the stochastic parameters of a network design model [3].
In [18], a methodology for scenario development, in which every scenario must be selected based on its impact on the studied process, is proposed. In [19], a locating model that involves production planning through scenarios is presented. A variation of this model is introduced in [20]. In [3], the design of a multi-product chain with multiple echelons, utilizing approximation based on scenarios, is addressed. The system is modeled as a mixed-integer linear programming model, which objective function is to minimize the network total costs.
In [21], a location dynamic problem is solved by means of using scenario trees. In this study, causal correlations between scenarios are shown, which are evaluated according to the methodology described in [22].
Some works have considered the generation of scenarios for supply network design [23-26. In [23], the design of a multi-stage and multi-objective supply network is approached. The uncertainty in the problem is represented by a combination of scenarios with a given occurrence probability. The maximization of the NPV in the supply chain, and the minimization of the financial risk are the objective functions to be optimized. In [24], a methodology to model risks in the supply chain design with uncertainty is proposed, and validated with real applied cases. A network design model that integrates financial factors under demand uncertainty has been proposed in [25]. Finally, in [26], a supply network design problem, considering economies of scale and demand variation, is proposed.
Two interesting cases of successful applications of supply chain design can be found in [27 and [28]. Ramírez et al. [27] propose, for the study of a supply chain, an analytical model based on local systems dynamics, minimizing the distance between the chain echelons. García-Cáceres et al. [28] suggest a simple period mathematical programing model for a 5-stages supply chain with multiple ownership organizational possibilities in the distribution channels; this case considers transfer prices, economies of scale, agreements among agents, and inventory considerations for a regional setting.
III. Distribution network optimization
This paper addresses the design problem of a distribution network of massive consumption products, considering the maximization of the investment's Net Present Value (NPV). The network comprises a distribution system of three echelons: plants, distribution centers, and clients. A stablished network design (located plants and clients) is the starting point, in which the central problematic is determining the opening of distribution centers, and the allocation of product flow throughout the network.
The proposed mixed-integer linear programming model is multistage and multi-period. Particularly, this research has considered the whole logistic infrastructure in a single country, a planning horizon of five years, and the product demand variation at each consumption zone at every period of time. The product demand at each consumption zone (clients) is variable, with a known probability distribution. To model the demand variability, three demand scenarios with equal occurrence probability are considered [1]. Variability in response times is not included, and it is considered a constant factor for the entire product flow along a specific route. Distribution centers have enough capacity to manipulate, receive, dispatch, and store all necessary product flow. Similarly, transportation among different distribution centers is considered, as well as a sufficient fleet of homogeneous vehicles.
A. Sets, variables and parameters
The proposed model considers the following main sets and parameters:
Main sets
PL = Manufacture plants, indexed by i
CD = Set of potential distribution centers, indexed by j
C = Set of geographic zones that represent th e customers, indexed by k
PT = Sets of finished products, indexed by p
T = Sets of time periods, indexed by t
S = Set of scenarios, indexed by s
Parameters
CTPCDijt = Transportation cost of the finished product p ( PT from the plant i ( PL to the distribution center j ( CD in the period t ( T [$/ units of p].
CTCDCDjj*t = Transportation cost of the finished product p e PT from the distribution center j ( CD to the distribution center j * ( CD in the period t ( T [$/units of p], j ≠ j*.
CTCDCjkt = Transportation cost of the finished product p ( PT from the distribution center j ( CD to the client k ( C in the period t ( T [$/ units of p].
CPipt = Variable manufacturing cost of the finished product p ( PT in the plant i ( PL in the period t ( T [$/units of p].
CMjpt = Cost of the finished product inventory maintenance p ( PT j ( CD in the distribution center in the period t ( T [$/units of p].
CFit = Plant operation fixed costs i ( PL in the period t ( T [$/period].
GADCDjt = Plant amortization and depreciation expenses j ( CD in the period t ( T [$/ period].
CFUJt = Distribution center fixed operation costs j ( CD in the period t ( T [$/ period].
GADCDjt = Distribution amortization and depreciation expenses j ( CD in the period t ( T [$/ period].
PCAPipt = Penalization cost for manufacturing one extra unit p ( PT, exceeding the plant production capacity i ( PL in the period t ( T [$/ units of p].
VIPTjt = Product handling cost p ( PT in the distribution center j ( CD in the period t ( T; [$/ units of p].
CAPLi = Plant's production capacity i ( PL for all products p ( PT [units of p/year].
CAPCDj = Distribution center flow capacity j ( CD for all products p ( PT [units of p/year].
Ppkt = Finished product sale price p ( PT to the client in the period t ( T [$/units of p].
DEMkpts = Client's demand k ( C for the finished product p ( PT in the period t ( T and scenario s ( S [units of p/ period].
Invj = Initial investment to open the distribution center j ( CD [$].
WACC = Cost of the capital invested by the company.
TIMP = Income tax rate.
The model utilizes the following set of variables
Decision variables
Binary variables
W j = 1 if it is decided to invest in the construction of a distribution center j, 0 otherwise.
Flow variables
Xijpst = Amount of finished product p ( PT shipped from the plant i ( PL to the distribution center j ( CD in the period t ( T and scenario s ( S [units of p/period].
yjkpst = Amount of finished product p ( PT shipped from the distribution center j ( CD to the client k ( C in the period t ( T and scenario s ( S. [units of p/period].
Ujj*pst = Amount of finished product to be shipped from the distribution center j ( CD to the distribution center j*( CD in the period t ( T and scenario s ( S, where j≠j*. [units of p/period].
V pjst = Amount of finished product p ( PT final inventory stored in the distribution center j ( CD in the period t ( T and scenario ( S. [units of p/ period].
Capadits=Additional production capacity to be considered in the plant i ( PL in the period t ( T and scenario s ( S.
B. Demand scenarios
This paper considers demand scenarios for each product at every consumption zone. The scenarios were generated following the methodology proposed in [1]. Particularly, the scenarios considered in this paper were base, pessimistic, and optimistic. The base scenario corresponds to the average demand values, and the pessimistic and optimistic scenarios correspond to the confidence interval extreme values of the demand statistical distribution. In particular, the lowest extreme corresponds to the low or pessimist demand values, and the superior extreme, to the high or optimistic demand values. To calculate the confidence intervals, the general methodology based on pivot functions [29] for every probability distribution is used.
In order to calculate the objective function, the probability of each scenario is assumed to be known, and all scenarios () are equally probable ( = 1/3, for , that is, they all have the same occurrence probability. These probabilities must satisfy equation (1).
C. Proposed mathematical model
According to the considerations described in sections 3.1 and 3.2, the network optimization mathematical model base on scenarios is formulated as follows:
Where:
Where [ ] + and [ ] - correspond to the positive (>=0), and negative (< 0) parts, respectively. The equations to calculate the factors that compose FCLst are detailed as follows:
The objective function of the mathematical model considers the NPV maximization for all considered scenarios [2]. Note that NPV considers the present value evaluation of the free cash flow discounted to the Company's capital cost, minus the initial investment of the opening of distribution centers.
Calculating the free cash flow for each period tGT, the following costs and expenses have been considered: finished product transportation costs from plants to distribution centers [6], finished product transportation costs between distribution centers [7], finished product transportation costs from distribution centers to clients [8], plant's production variable costs [9], maintenance costs [10], manipulation costs [14], finished product inventory costs in distribution centers, and penalization costs for using plant's additional capacities [13], fixed costs, and depreciation and amortization expenses in plants [11], and in distribution centers [12]. The results were compared considering the minimization of the present value of costs and expenses (PEC) as the objective function (21).
Equations (16) and (17) restrict the capacities of the plant and distribution center, respectively. The set of restrictions [18] determines the product balance in distribution centers. The set of restrictions [19] ensures the product's demand compliance, at every consumption zone, for every scenario, and at every period of time. Finally, the set of equations (20) considers the no-negativity and integrity of decision variables.
Like in [1], the structure of the network distribution is assumed as independent from the evaluated scenario.
IV. Computational results
The mathematical model has been accepted according to the characteristics of the Company study case. The Company has 62 product families that in this case correspond to the PT set. The time horizon is 5 years. In this case, 4 potential plants and 10 distribution centers are considered. Clients are aggregated into 48 consumption zones. The Company's capital cost (WAAC) is 22 %, and the income tax rate (TIPM) is 35 %.
The mathematical model was implemented in C++, and the experiments were conducted in an Intel Core i7 (2.80 GHz) computer with OS X Yosemite, and 8 GB of RAM. Demand distributions were obtained with the software Oracle Crystall Ball(. The solver optimization used was CPLEX 12.6. The parameters were projected using the Predictor tool in Oracle Crystall Ball(.
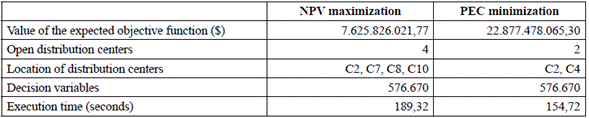
Table 1 summarizes the results of the proposed mathematical model with the two objective functions (NPV maximization and PEC minimization). Table 1 shows the values of every mathematical model objective function, which were described in section III.C. Likewise, the number and location of open distribution centers are reported, as well as the computational statistics on number of decision variables and execution time.
The number of distribution centers (model's final solution) is completely different. Considering NPV maximization, the optimal number of distribution centers is 4, whereas that considering the alternative objective function, the number is 2 (Table 1); this is mainly due to the sale prices effect on the market zones. Similarly, the potential location of the distribution centers significantly differs (Table 1), confirming that ignoring financial criteria in decisions about distribution network design may reduce the company's profitability. Moreover, it is important to mention that the variability of the demand between the two models might lead to erroneous decisions on the network distribution configuration.
V. Conclusions and future work
Considering financial criteria in the design of distribution networks is a poorly explored area of research, but one that has great potential to be developed within the operations research community. Additionally, the network design problem is highly complex, due to the inherent risk in the demand values at every consumption zone. Recently, this issue has received attention from the scientific community, which has proposed several methodologies based on scenarios.
This study proposes a mixed-integer linear programming model that takes into account financial criteria and scenarios to involve the demand variability at different consumption zones. In contrast to traditional methods, the methodology developed here considers the network design problem as an investment decision, which must be closely related to a return or profitability over the invested money. The results show the importance and efficiency of the proposed methodology as an alternative to the distribution network design with stochastic parameters for companies of massive consumption products. Evidently, as the number of distribution network stochastic parameters increases, methodologies, such as SAA [6], with more robust solutions may be applied.
The results of this research are important as a precedent to approach and solve real problems in the supply network design, considering financial factors and the demand variability. Future research should consider other financial objective functions, such as the minimization of the financial risk by means of the Value at Risk (VaR). Furthermore, other methodologies to solve lineal stochastic programing problems might be considered. Finally, decisions on transportation mode, type of vehicles and routes to be performed together, might be included in the mathematical model such as considered in [30-33].