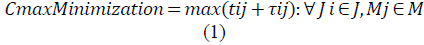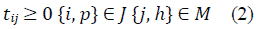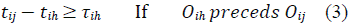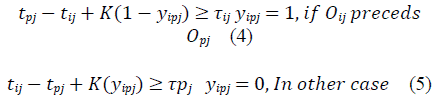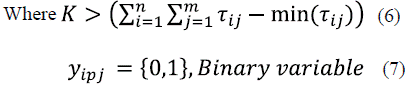I. Introduction
The Job Shop Scheduling Problem (JSP) is one of the most studied scheduling problems in the literature [1]. Like other scheduling problems, it is classified as a problem of combinatorial nature since it requires to develop a configuration for programming a set of jobs in a set of machines, where each job has a series of operations that must be processed in a defined sequence, and in an established processing time. In most of the job shop scheduling cases, it is desirable to find the best configuration to minimize the makespan (total time where all jobs have been executed). Other goals directly related to timing are the minimization of tardiness, delay, and total flow. The JSP is considered an NP-Hard problem [2]; hence, it is computationally difficult to find an optimal solution in a reasonable time since the search space grows exponentially as the problem entries increase.
Since the early 1950's, numerous researches have focused on solving the JSP. In 1956, Jackson [3] proposed a new approach by generalizing the Johnson's Flow Shop algorithm [4]. Akers and Friedman [5] employed an algebraic approach to represent the processing sequences. Subsequently, Roy and Sussmann [6] proposed a representation with the disjunctive graph; and finally, Balas [7] applied an enumerative approach based on this graph. Among the different approaches for solving the JSP, it is common to find exact methods that aim to find optimal solutions at a high computational cost; however, they turn out to be efficient only for small applications. Applegate and Cook [8], and Brucker et al. [9] solved the Ft10 Benchmark problem, and tried with applications up to 30 jobs and 10 machines for the JSP, using the Branch and Bound method; other applications of this method are covered in [10,11]. For some larger applications, however, some approximations such as heuristic algorithms are required. Some of them include priority dispatching rules [12,13], and the mobile bottle neck algorithm [14,15]. Recent researches have mostly focused on more advanced heuristic algorithms, better known as "metaheuristics", which propose several approaches like the tabu search [16-19], simulated annealing [20-22], ant colony optimization [23-26], particle swarm optimization [27-30], neuronal network [31,32], and genetic algorithms (GA). In particular, the GA are based on Darwin's evolutionary theory, and they have been employed to provide successful solutions to various combinatorial problems (JSP included [33-36]) since they allow exploring in an efficient way the solution space; nevertheless, they may converge prematurely. That is why recent researches have aimed to combine the GA with other techniques that ameliorate its efficiency by developing hybrid methods as the Memetic Algorithm (MA).
The MA was first introduced by Moscato and Norman [37]. The basis of the MA lays on individual enhancements of the solutions of agents that interrelate one to another in a process that contains stages of cooperation and population competition. The MA has been successfully used in different areas and combinatorial problems, such as the knapsack problem [38-40], routing problems [41-43], quadratic assignment [44-45], and spanning tree [32,46], among others. In order to give a solution to the JSP, some studies [1,47-50] have proposed a MA, where the global search given by the GA is combined with a neighborhood structure based on Nowicki and Smutnicki [51], which allows the leading of the local search and the efficient exploitation of the solution space with the generation of three adjacent solutions for each initial solution; all of this with the final goal of minimizing the makespan. Here, we review the literature related to solve sequence problems with evolutionary "metaheuristics" algorithms, taking into account the JSP and the MA. In addition, we designed an algorithm to minimize the makespan, and studied the representation of the solution with chromosome, based on operations, and various ways of starting and building the solutions. Likewise, we fixed and established the genetic operators, as well as the searching algorithm, and designed an experiment to measure the effect of the algorithm parameters on the outputs. Finally, we evaluated the algorithm efficiency with reference problems from the OR-Library.
This paper is organized as follows: section 2 describes the JSP; section 3 presents the MA framework; section 4 analyzes the effect of the algorithm parameters on the makespan by experimentation, and evaluates the MA with benchmarking problems; and section 5 summarizes the conclusions.
II. Job shop scheduling problem definition
The JSP consists in a set of jobs that must be processed in a limited set of M machines. In the JSP, the following restrictions and assumptions are considered:
Each machine is able to process one job at a time.
Each job can be processed by only one machine at a time.
The sequence of machines that a job visits is completely fixed, and has a linear precedence structure.
All jobs must be processed for each machine only once, and there is a maximum of operations per job.
Machines are always available and never interrupted.
The processing time of all operations is known.
The JSP mathematical model is presented in equations (1) through (7). Equation (1) represents the makespan minimization function; meanwhile, equations (2-7) represent the problem constraints.
t ij : Beginning time of each operation
J: Set of n jobs to be processed
M: Set of m machines
Oij: Job operation that must be processed by a machine in an interrupted time
Subject to:
III. Memetic algorithm for the job scheduling problem
The general procedure for the development of the memetic algorithm (MA) is shown in the following pseudo code.
The memetic process begins with the generation of the initial population. For that purpose, the population size parameters are established as well as the number of generations, selection probability, and mutation. The initial population is a set of solutions presented as chromosomes that are decoded afterwards. A searching method is then applied to these solutions in order to generate adjacent (or neighbor) solutions. Subsequently, each individual from the initial population, as well as the chosen neighbors, are decoded and evaluated to obtain the makespan value. If the algorithm's termination criterion has been accomplished, the program stops and shows the best-found solution; if not, a new population is generated using the genetic operators' application (selection, crossing, and mutation) over the population. These new individuals are known as a generation, and the previous procedure is then repeated until the breakdown criterion is accomplished. The following sections describe each stage of the algorithm.
A. Chromosome coding and decoding
In the JSP solution using MAs, the coding is given by a chromosome for each individual that represents the programming or the schedule. The main purpose is to generate feasible schedules, avoid any reparation to individuals, and easily apply the genetic operators. In this study, we used the representation based on operations, which allows to code the schedule as an operation sequence.
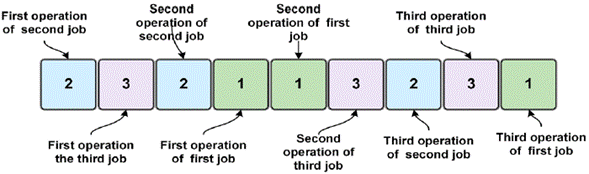
For a given problem of jobs and machines, a chromosome is a permutation with job repetitions and genes. The operations are represented by the number of each job, and they appear several times in the chromosome. Each appearance of a same number indicates an operation within the programming sequence for the given job. This type of representation always generates feasible programs. For example, a chromosome [2,3,2,1,1,3,2,3,1] is given, where 1, 2, and 3 correspond to jobs. Each job is repeated as many times as the number of machines the problem possesses, and they represent the operations for each job. In figure 1, by reading the chromosome from left to right, the first gene (2) represents the first operation of the second job to be processed first on the corresponding machine. The second gene (3) represents the first operation of the third job. Therefore, the third gene (2) represents the second operation of the second job because it is the second time this number appears in the chromosome. In this way, the chromosome [2,3,2,1,1,3,2,3,1] is a sequence (operation of job) that can be translated as an operation vector O 21 0 31 O 22 O 11 O 12 O 32 O 23 O 33 O 13 .
The Gantt's diagram, which is used for schedule decoding, results from reading the genes in a chromosome from left to right, and programming operations considering the corresponding processing times and machine sequences. Each operation is assigned in the minimum possible time without violating constraints.
B. Initial population
Different methods have been proposed to generate the initial population: heuristics, as the mobile bottle neck [10], priority dispatching rules [9], or random approaches. This study uses the random generation of individuals because any job permutation will be a feasible schedule, due to the chosen representation type. An individual is a vector that contains positions, and is generated by randomly assigning the number of each job. This is repeated until achieving the population size.
C. Genetic operators
Genetic operators allow the population to evolve by generating new individuals with the main purpose of ameliorating the offspring, as well as exploring new searching space solutions. The used operators are selection, crossover and mutation.
The selection scheme combines both tourney and roulette selection. Basically, it consists on choosing the parents as a probability of the best population individuals, but at the same time allowing some not-so-good individuals to be part of the selected group.
The chosen chromosomes form half of the previous population, and they are called parents.
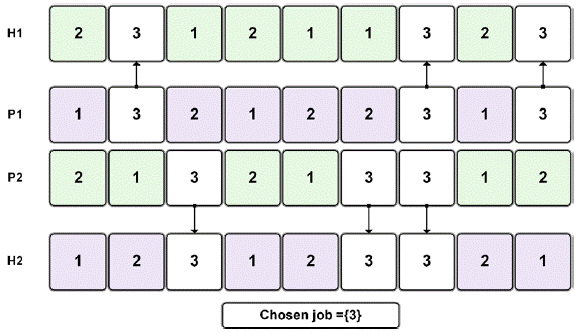
In Crossover, first, a pair of parents (chromosomes) are randomly selected from the mating pool, and then new offspring is created by exchanging the parents' genetic information. Two parent strings are denoted as P1 and P2, and two children strings are denoted as H1 and H2. The procedure consists on randomly choosing one job, any gene in the parent P1, which is then retained in the same position in child H1; subsequently, the remaining empty positions in child H1 are filled with the genes of parent P2 that are different from the chosen job. The second child is generated in the same way, but exchanging the parent's role (Fig. 2). This operator is known as JOX (Job Order Crossover) [52].
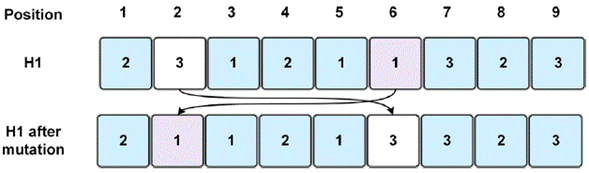
Mutation introduces some extra variability into the population, and prevents its premature convergence. Each child generated with the crossing operator has a mutation probability associated (random number between 0 and 1), which is compared to a designated parameter at the beginning of the algorithm. If the mutation probability of a child is less or equal than the probability parameter, the mutation is then executed; otherwise, the individual is kept with no changes. The mutation procedure exchanges the position of two genes within the chromosome. For instance, in figure 3, the chosen numbers are 2 and 6, which means, they are the positions to be exchanged. The first operation for job 3 is found in position 2, which will be moved to position 6, and the last operation for job 1 that is on position 6 will be moved to position 2. In this way, a child is altered, and the schedule is modified.
D. Local searching procedure
The memetic algorithm (MA) modifies the neighborhood strategy proposed by Nowicki and Smutnicki [51]. Nowicki and Smutnicki's proposal is based on the critical route, also known as N5. However, in the MA, the decision on the schedule's critical route, in which local searching will be applied, is not random; on the contrary, the decision is made choosing the longest known route for that programming. In other words, the chosen route is the one with the largest number of critical operations. The main purpose of applying this neighborhood structure is to reduce the amount of movements by omitting some movements (proposed by Van Laarhoven et al. [19]) that will not immediately improve the makespan. The operation exchanges are only made in the block borders. The procedure consists on exchanging the last two operations of the first critical block, and the first two operations of the last block in the selected critical route. To perform this operation, some of the chosen blocks must contain at least two operations.
Using this local searching method, three neighbors (, and) are obtained from the chosen route: one neighbor per each executed exchange, and the third one from the two simultaneous exchanges. If the chosen critical route contains only one block, it is possible to generate only one neighbor. Once the three neighbors are found, the operations programming order is modified in the schedule. Afterwards, a decoding is carried out on Gantt's diagram, where the neighbor with the best fitness function value (makespan) will continue into the procedure performed by the genetic operators. If only one neighbor is generated, it will immediately advance to the selection process.
The local searching pseudo code is presented as follows:
IV. Computational results
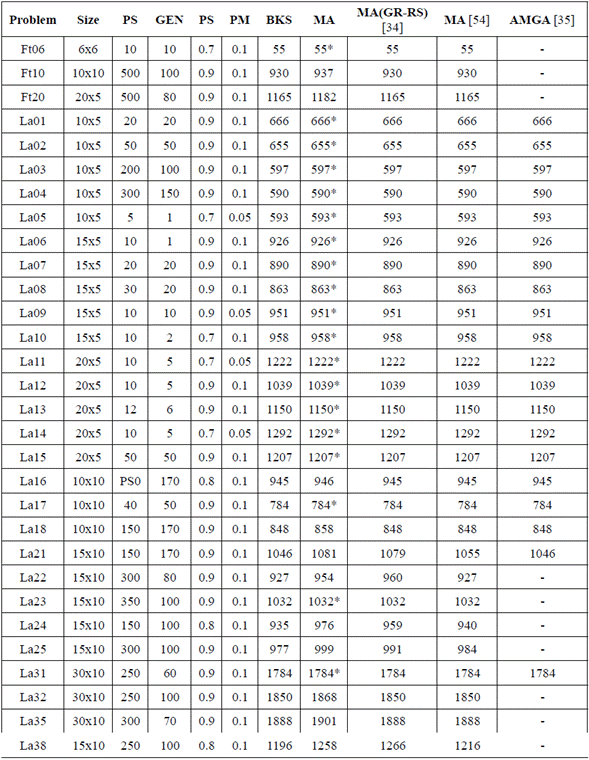
A fractionated 2k-1 experiment was designed to select the best parameters to execute the numerical experiments. Population size, number of generations, selection percentage, and mutation probability were considered factors that may affect the computational performance. The experiments were performed using benchmark problems from Fisher et al., better known as FT, and Lawrence's, better known as LA, all of them taken from the OR-Library [52-53]. For the first experiment, low and medium complexity problems (Ft06, La01, La06, La09, La11, La14, and La17) were used; meanwhile, for the second experiment, problems of high complexity (Ft10, Ft20, La16, La21, La 24, La25, and La 38) were used. For low and medium complexity instances, 8 replicates were made per each combination or treatment, while 5 were made for high complexity instances. The low and high values of each factor used in the low and medium complexity instances were population size {10, 30}, number of generations {20, 30}, selection probability {0.7, 0.9}, and mutation probability {0.05, 0.1}. The values for high complexity instances were population size {80, 150}, number of generations {100, 170}, selection probability {0.8, 0.9}, and mutation probability {0.05, 0.1}. The numerical experiments were developed in the Matlab® programming environment, in a PC with an Intel Core i7 processor, 3.40GHz, and 8GB memory. According to the analysis of variance (ANOVA), population size, number of generations, and selection percentage affect the solution; therefore, the ANOVA results allowed to adjust these factors, achieving a positive impact in most of the outputs. We found that mutation probability has a low significance in the evolutionary process, confirming the literature findings regarding this operator [54].
Table 1 summarizes the results of the experiments. The columns include the name of each test benchmark problem (Problem), the size of the problem (Size), the population size (POP), the number of generations (GEN), the selection probability (SP), the mutation probability (MP), the value of the best-known solution for each problem (BKS), the value of the best solution found by using the proposed MA (MA), and the solution obtained from other evolutionary approaches made by Hasan et al. [55], Gao et al. [52], and Wang et al. [36]. The solutions marked with an asterisk (*) are optimal. The proposed MA found the best-known solution in 19 instances (63.3 %) among the 30 evaluated problems. Also, the propose MA found 10 solutions worse than other approaches; however, the gap respect to BKS is less than 2 % in 87 % of the evaluated problems (Table 1).
V. Conclusions
This study developed a memetic algorithm (MA) to solve the Job Shop Scheduling Problem by using the JOX method in the crossing operator, and a new neighborhood structure for the local searching procedure. This new neighborhood structure generated three new solutions by exchanging operations in the first and last block of the critical path. The MA takes advantage of the genetic strategy that explores the solution space, and the local searching method, which intensifies the searching by exploiting every found solution to avoid being trapped in a local optimum. The random generation of initial individuals was successful to diversify the population, and the decoding was the process with the longest computational time. From the ANOVA, we can conclude that the population size is associated with the exploration capacity of the memetic algorithm. The MA was evaluated in 30 benchmark problems, and compared with the solutions obtained in the literature; the computational results obtained from the experiments demonstrated the efficiency of the proposed memetic algorithm.