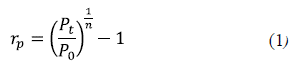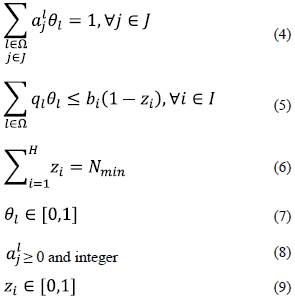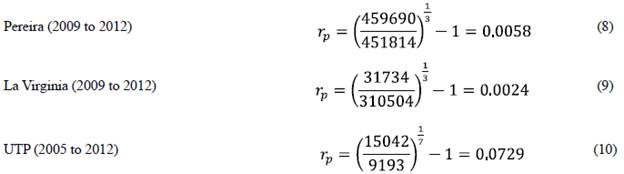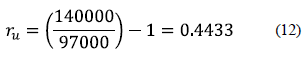I. INTRODUCTION

The Colombian automotive market is more aggressive everyday regarding sale strategies, proposing a big quantity of opportunities for buying vehicles, discouraging public transportation use, and causing an unstoppable increase in traffic that has led to a great urban congestion in many cities. The fleet of vehicles and motorcycles is bigger every day, the parking zones in the city centers are insufficient, and the road infrastructure collapses faced with the traffic flow in the rush hours. This is why nowadays, proposals that include a complete, effective, and environmentally respectful public transportation, and that integrate an important part of the city areas have gained great interest in the community.

The urban transport, as a whole, is an activity of important magnitude for a country. The operation of vehicles that circulate in roads of Latin American and the Caribbean cities with populations higher than 100,000 inhabitants consumes close to 3.5 % of the GDP ¹. In the case of Colombia, the National Government implemented a policy known as CONPES 3197/2002 [2] for improving the service of urban public transportation for passengers, followed by the CONPES 3197/2002 ² for improving the urban and public transportation service for passengers, and the CONPES 3260/2003 ³ for urban and massive transportation. These policies were implemented after analyzing the transportation deficit in populations with more than 500,000 inhabitants, and high level of development and growth, which led to the conclusion that the suitable solution was to implement integrated massive transportation systems. So far, these systems have been implemented in several capital cities as a solution to the urban mobility issue, but five of them have not achieved the projected goals, due to the competition with other means of transportation (formal and informal).

Pereira is one of those five cities that have not reached the goal number of transported passengers, which should be around 140,000 per day. Nowadays, 90,000 passengers are being transported, indicating that there is still a deficit of 50,000 daily passengers to reach the break-even point. Hence, the challenge is to expedite the integration process into the metropolitan area ⁴, and to achieve that, a methodology from a mathematical-optimization perspective is presented in this paper. The methodology proposes a design of feeding routes for zones disconnected from the mass transportation system (MTS). The feeding routes are integrated to the interchange station or stop points, taking as reference the record available in the origin-destination matrix, and projecting them to the date of study.

The contributions of this paper are the following: 1) a methodology for generating feeding routes in unintegrated sectors of the MTS that introduces an analogy to the Location-Routing Problem (LRP), and 2) a strategy for integrating disconnected zones from the MTS, in order to reach a break-even point regarding the number of passengers, and thus achieve its economic viability, so wider service coverage is attained.

II. DEMAND FORECASTING

The compound annual growth rate (CAGR) of the population growth is the traditionally used measurement in the business and investment fields for estimating the profits in a time lapse ⁵. The computation of the population growth rate for cities and communities has been applied to the U.S. prison population ⁶, to the forecast of methane emissions in Delhi, as a consequence of its population growth, and to scientific papers written by mathematicians on global population growth ⁷. The demand forecast was calculated using (1) and (2), as proposed in ⁵.

Where ^_rp = population growth rate per time unit, ^_Pt = population in the year t, P₀ = population in the year 0, n = number of years, ^_ru = user's growth rate based on the forecast demand, ^_Df = future customers demand, ^_DA = current customers demand.

III. LOCATION-ROUTING PROBLEM

The Location-Routing Problem (LRP) can be defined as a finite set of potential depots I with a fixed opening cost ^_fi and capacity b_i and a set of costumers J, where every costumer has a demand ^_dj. A homogeneous vehicle fleet with a limited size must be routed from the depots for attending customers demand. Every vehicle has an associated capacity Q, and every pair of nodes, i and j, has an associated traveling cost ^{_{cij (} 8}

The objective is to determine the set of depots that must be open, the order for visiting the customers, and the allocation of routes to the opened depots. All these actions must be performed minimizing the total operative costs, which represent the opening depots costs, the opening routes costs, and the costs associated to the utilization of the active arcs ⁹.

Several authors have focused on developing heuristic methods for finding solutions in computationally reasonable times. Nagy and Salhi ¹⁰ classified these algorithms as sequential, iterative, hierarchic, and clustering-oriented. The sequential methods initially solve the depots location, and then the routes associated to every depot; however, this type of methodology reduces the feedback between both problems, and thereupon is inadvisable ¹¹. The iterative methods solve both sub-problems simultaneously, and give permanent feedback through the obtained outputs from every sub-problem separately; these strategies applied to the LRP solve the problem without considering the locating variables, allocating one depot for every set of customers, and at least one route to the open depots ¹². The hierarchical methods consider depots location as the main problem, and the routing problem as a subordinated problem; first, the location problem is solved in an approximated way, and then, an associated subroutine to the corresponding routing problem is added ^{(13 14)} The methods based on clustering customers were proposed by Barreto et al.¹⁵.

In the first phase, the set of customers is divided into groups depending on the vehicle capacity. In the second phase, a Traveling Salesman Problem (TSP) is solved for every cluster. In the last phase, every TSP tour is clustered in super nodes to solve the capacitated depots location problem.

To solve big-sized instances, Prins ^{_{et al. (} 16}, Prodhon ^9,17,18 Duhamel ^{_{et al. (} 19} and Escobar ^{_{et al. (} 20} proposed several metaheuristics; among them, the techniques based on Granular Tabu Search (GTS) have been the most efficient for solving instances of up to 200 customers. The methods combine Integer Lineal Programming (ILP) models using Lagrangean relaxation for setting up the routes. Pirkwieser and Raidl ²¹ proposed the Variable Neighborhood

Search (VNS) for solving the Periodic Location Routing Problem (PLRP), and the CLRP approached through a combination of a VNS with the sequential solution of a ILP. The considered ILPs are two-index models aimed to solve the location problem, and the reallocation by means of a set-partitioning model (SP).

Yu ^{_{et al. (} 22} proposed the Simulated Annealing algorithm, where diversification is controlled according to the temperature parameter, in order to escape from local optima. Better gaps were found using the proposed methodology, compared to the ones found in ^{(16 19)}; also, the location-allocation concept is introduced, where the location and routing decisions are made simultaneously. In Hemmelmayr ^{_{et al. (} 23}, the Adaptive Large Neighborhood Search heuristic (ALS) was developed for the LRP. In this technique, different neighborhoods are applied and classified according to the obtained results; for the following iterations, the best scored neighborhoods have the higher possibilities to be selected.

Furthermore, the LRP has been solved throughout exact techniques, including the Branch-and-Bound method ²⁴, column generation, Branch and Price ²⁵, and Branch and Cut ²⁶. These methods solve instances of up to 200 customers, but some instances of 100 customers are still unsolved. Prodhon and Prins ²⁷ presented a complete study on problems associated to the LRP, where models, solution methodologies, and a comparison of the results obtained using the best algorithms are encompassed, analyzed, discussed, and classified.

IV. PROPOSED MATHEMATICAL MODEL FOR DEFINING FEEDING ROUTES

The solved model is based on the formulation presented by Akca ^{_{et al. (} 25} that corresponds to a SP model for the LRP. Ω is defined as the set of all possible routes starting and finishing in the depot (interchange station) i ∈ I subserving a subset of clients (bus stations) of at least two customers with a demand q_l. For every l ∈ Ω a binary variable θ₁ equal to 1 is associated if I appears in the optimal solution of the LRP, and 0 otherwise, and a C_lcost for using a route. For every client (bus station) j ∈ J, where J corresponds to the set of bus stations, and the route l ∈ Ω is assigned to the variable a^l _j , which corresponds to the number of times the customer j appears in the route ^{_{L, zi}} is a binary variable that is 1 if the depot (interchange station) i is used as the starting and ending point of the feeding route, and 0 otherwise. ^_Nmin represents the number of closed depots (interchange stations).

Subject to

The objective function (3) formulates the feeding-routing cost minimization, and the interchange stations use. Constraints presented in (4) indicate that a bus station can only be allocated to one route, so there are as many constraints as existing bus stations. Constraints (5) indicate that the accumulated demand of bus stations included into the feeding routes do not exceed the interchange stations capacity; there are as many constraints of this type, as considered interchange stations. Constraint (6) assures that the interchange stations that remain closed must be equal to ^_Nmin ; this constraint has been added to the original model, and represents a valid cut for the model, guaranteeing that only a set of suitable interchange stations will be added, the ones strictly necessary for attending the feeding routes demand. Finally, (7), (8), and (9) define the variables nature.

V. PROPOSED METHODOLOGY

According to the bibliographic review, we can make an analogy between the LRP and the feeding routing problem, where the depots are equivalent to the interchange stations on the backbone, the customers are associated to the interchange stations, and the demand is associated to the number of passengers required to board the vehicle at a determined bus station. Like in the LRP, the route is designed and connected to the closer interchange station in the MTS backbone.

The proposed methodology includes demand forecast and a math-heuristic developed in three steps: 1) a big tour construction over a network of possible bus stations in a disconnected zone; 2) generation of n possible route alternatives that are subsequently connected to one or more points on the backbone, and identification of n possible circular routes that will be sent as input of the third step; 3) use of a Mixed Integer Linear Programming problem (MILP) to identify the set of routes attending the bus station demands, considering as objective function the travel time minimization.

A. Math-heuristic for solving the problem

The problem solution is described in three steps:

Step 1. Grand tours attainment. This step consists in generating three TSP or grand tours with the bus stations of the route to be designed, using three different techniques: 1) Clark & Wright Savings ²⁸, 2) Walk, and 3) Nearest Neighborhood. All three tours are improved using them as the Lin-Kernighan-Helsgaun algorithm (LKH) input, an improved version of the traditional Lin-Kernighan algorithm developed by Helsgaun ²⁹.

Step 2. Route Segmentation. A tour-partitioning is performed to the three grand tours, using the Prins algorithm [30]; then n routes are obtained and connected to the interchange stations considered in the study. Infeasible solutions in terms of vehicle capacity and time duration are discarded.

Step 3. Mixed Integer Linear Programming (MILP) solution. The routes generated in the is solved using the Branch-and-Cut algorithm. The MILP solution is defined in equations (3) to (7).

1) Proposed algorithm: The algorithm is presented in Algorithm 1. The required input parameters are added in lines 2 to 7.

Step 1: To obtain grand tours, the LKH and the savings algorithms were used (lines 8 to 20).

Step 2: To generate feasible routes, they are built starting with a single client up to k clients, considering the vehicle capacity and time constraints. This step is performed for every grand tour previously obtained (lines 21 to 26).

Step 3: To solve the PLEB Model using the CPLEX software, the inputs for the model are the set of routes Ω_l the set of demands q_l , and the set of times c_j.

Algorithm 1 Algorithm for adding feeding routes into a MTS by using the proposed methodology. 

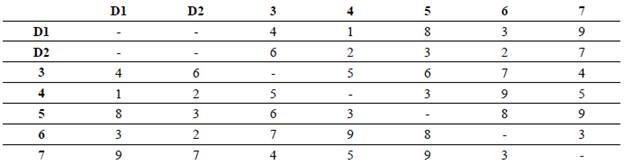
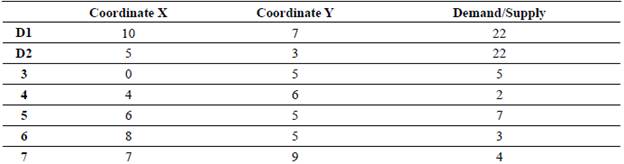
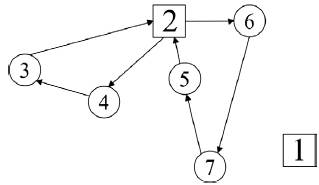
2) Applied example: We used a system of five bus stations (3, 4, 5, 6, and 7) located in a disconnected zone, which must be attended from the interchange stations D1 and/or D2 that are placed on the backbone.

Table 1 and 2 present the input data.

Table 1 Time Matrix 

Table 2. Coordinates and demand/supply of passengers per bus/interchange station

Step 1. The grand tours were generated by using heuristic techniques, considering the bus stations described in Table 1. We obtained three sequences where depots D1 and D2 are not included: a) 3-4-5-6-7; b) 6-7-5-34; c) 5-7-4-3-6.

Step 2.k_n possible feeding routes were generated for every sequence, where k represented the number of depots. Every feeding route corresponded to a decision variable for the BILP. In this step, we verified the alternative to quantify time and demand for determining the feeding routes feasibility. We considered a homogeneous fleet with a capacity of 15 passengers per vehicle, and a maximum time per route of 25 minutes.

Table 3 shows some of the obtained feeding routes with their respective time, capacity, and feasibility. Figure 1 shows the optimal solution of the example.

TABLE 3 Set of feeding routes generated with their respective time, capacity, and feasibility 

Sequence	Time	Capacity	Feasibility	Route
131	4+4=8	5	Yes	#1
2 3 2	6+6=12	5	Yes	#2
1 3 4 1	4+5+1=10	5+2=7	Yes	#3
2 3 4 2	6+5+2=13	5+2=7	Yes	#4
1 3 4 5 1	4+5+3+8=20	5+2+7=14	Yes	#5
2 3 4 5 2	6+5+3+3=17	5+2+7=14	Yes	#6
1 3 4 5 6 1	4+5+3+8+3=23	5+2+7+3=17	Only time	No
2 3 4 5 6 2	6+5+3+8+3=24	5+2+7+3=17	Only time	No
1 3 4 5 6 7 1	4+5+3+8+3+9=32	5+2+7+3+4=21	No	No
1 6 7 5 1	3+3+9+8=23	3+4+7=14	Yes	#m
2 6 7 5 2	2+3+9+3=17	3+4+7=14	Yes	#m+1
2 5 7 4 3 2	3+9+5+5+4=26	7+4+2+5=18	No	No

FIG. 1 Optimal solution for the applied example. 

VI. STUDY CASE OF MEGABÚS: CENTRAL-OCCIDENTAL METROPOLITAN AREA SYSTEM (AMCO)

The study case started by updating the information for 2015 by incorporating the demand forecast methodology discussed in section 2. The basic information corresponding to Pereira and La Virginia municipalities can be found in ³¹. On the other hand, the information about the Technological University of Pereira (UTP) zone was taken from ³², and it was divided into zones in order to identify the user's origin points. The data forecast for 2015 was performed by using the growth rates obtained in (8), (9), and (10).

Growth rate for Pereira, La Virginia, and the UTP

The Megabus system currently mobilizes 90.000 passengers, but its objective is to reach 140.000; therefore, the demand must be projected considering the users growth rate factor denominated r_u.

A. Construction of the test cases

The AMCO zonification was applied using the transport zones analysis (ZAT). The bus stations coordinates, the origin-destination matrix, and the Pereira city zonification can be consulted at http://blog.utp.edu.co/problemasderuteo/?p=331.

The considered study cases were taken from every disconnected zone of the Megabús backbone, which are structured considering the proximity of the bus stations, the topography, and the city road design. Based on this information, the demand matrix was generated using Google Maps, and the traveling times among nodes were computed. The same value of r_u was taken for all zones to forecast the demand.

The r_p value used for the ZAT of 10 bus stations was the one found for the UTP. The current Megabús stations, hereafter called interchange stations, were codified with values between 1 and 100. For the Samaria zone, the bus stations are considered from 101 to 199, for the UTP zone, the bus stations are codified from 201 to 299, and for La Virginia zone from 301 to 399.

In total, we considered five study cases; every case had an associated bus station number that corresponded to the connection of the route to a station in the backbone, and the bus stations number. Table 4 presents the different scenarios.

• 1V: Scenario for La Virginia municipality. Time limit: 2 hours.

• 1S and 2S: Scenarios for the Samaria neighborhood. Time limit: 1 hour 10 minutes.

• 1UTP, 2UTP, and 3UTP: Scenarios for the Technological University of Pereira. Time limit: 1 hour 10 minutes.

Table 4 Scenarios. V: la virginia. S: samaria neighborhood. Utp: technological university of pereira 

Study case	Interchange Stations	Bus Stations
1V	1,2,3	301,302,303,304,305,306,307,308
1S	28,29,36	101,102,104,106,107,108,109,110,111,115,116,
117,118,119,120,127,128,132
2S	28,29,36	109,110,111,112,113,114,115,116,117,
118,119,120,122,123,124,127,128,129,132
1 UTP	6,7,8,20,21	204,205,208,216,217,220,221,228,229,230,231,232,
233,234,235,236,238,239,240,241,242,243,245,247,248
2 UTP	5,6,7,8,9,20,21	205,208,215,220,221,228,229,230,231,232,23,234,235
236,238,239,240,241,242,245,247,248,249,250
3 UTP	5,6,7,8,9,20,21,	206,207,208,209,211,212,213,214,215,25,239,240,
	22,23,29	241,242,243,244,249,250,251,252,253,254

The shown scenarios were disconnected from the MTS Megabús. For the circular routes generation, in Samaria and UTP zones, an infinite demand, and a limit time of 1 hour 10 minutes were considered. For the Virginia zone, a limit time of 2 hours was considered because it is an intermunicipal route.

Step 1: The grand tours or TSP were generated using as input the data presented in column "Interchange Stations" in Table 5.

Table 5 Solutions found for the proposed scenarios 

Step 2: The set of feeding routes was generated from the TSP obtained in Step 1. The Megabús interchanging stations are considered depots for generating circular routes between interchange stations and bus stations. Taking into account demand and time restrictions, the feeding routes were categorized as feasible or unfeasible. Thus, only the feasible routes were considered as decision variables for step 3.

Step 3: The MILP presented in equations (3) to (7) was solved to obtain the results shown in Table 5, where TEA represents the algorithm running time.

C. Feeding routes tracing

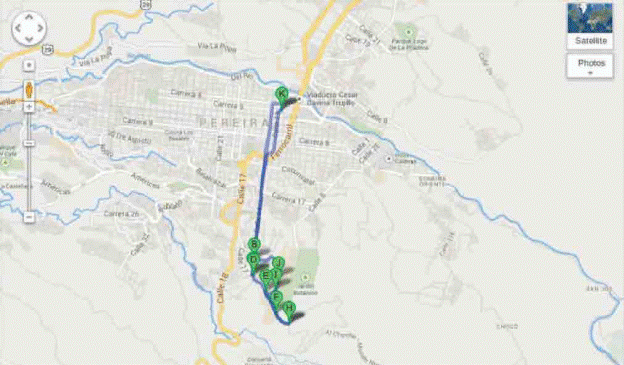
Feeding routes were identified for attending the disconnected zones, and thus integrating new users to the MTS, so the break-even point could be reached. Thereby, a viable system from an economic perspective may be generated. Figure 2 corresponds to the 1UTP solution.

FIG. 2 Solution route: Scenario UTP, feeding route 1. 

VII. CONCLUSIONS

An application to the Mass Transport System problem was developed for reaching the operational breakeven point. To solve the problem, the passengers forecast concept was incorporated, as well as the math-heuristic optimization method, combining heuristic optimization techniques to determine possible solutions, and an exact method to choose the best proposed alternatives. The feasibility criteria were met regarding the feeding route duration and the vehicle capacity.

The methodology described apply LRP concepts to the MTS, where the depots are equivalent to the interchange stations placed on the backbone. The set of costumers is associated to the set of bus stations, and the demand is associated to the amount of passengers who are required to board the route at a determined bus station. Like in the LRP, the route is designed and connected to the closer backbone interchange station of Megabús.

Many MTS operators still must reach their operative goals (number of users), due to the lack of feeding routes that would allow access to different locations of the city that represent potential sources of users. This is why this methodology attempts to meet the users demand and, from this information, establish possible feeding routes for accessing the system at a minimum cost, and satisfying the feasibility constraints related to vehicle capacity and route time duration.