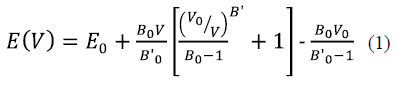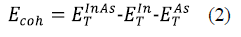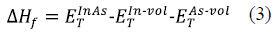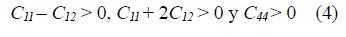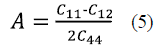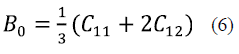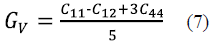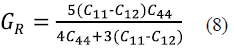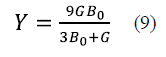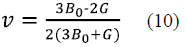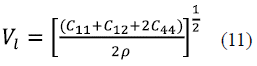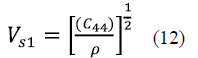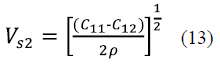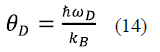I. Introduction
Indium arsenide (InAs) is a group III-V semiconductor compound with high electron mobility and a narrow direct band-gap. Under normal conditions, it crystallizes into a cubic zinc-blende structure 1, with a lattice parameter α = 6.058 Å (2, 3). This compound has been extensively studied because it provides a good basis for many commercial applications and new technologies, established in electronic and optoelectronic devices, such as light emitting diodes, photodetectors and lasers (4, 5). The operating characteristics of these electronic and optoelectronic devices depend not only on the materials engineering at a practical level, but also on a clear understanding of the material's properties and the fundamental science behind them. Therefore, theoretical and experimental investigations of the mechanical properties of the crystal, such as elastic constants (C11, C12 and C44), and the elastic properties derived from them -anisotropy coefficient (A), volumetric modulus ( B0 ), shear modulus (G), Young's modulus (Y) and Poisson's ratio (v)- are very important because they relate to several fundamental solid-state phenomena such as interatomic potentials and state equations 6-11. These elastic properties are also thermally related to the Debye temperature and the specific heat of InAs. Due to its technological importance, it is paramount to know the different properties of InAs; therefore, in this paper, we present the its structural, elastic, electronic and thermal properties, using the total energy calculation approach of the fundamental state of the system. These results provide a fundamental basis for understanding the physical properties of the InAs compound. All of the properties mentioned above were calculated using the local density approximation (LDA) and the generalized gradient approximation (GGA).
II. Computational methods
For the study and analysis of the structural, elastic and electronic properties of InAs, ab initio calculations were performed using the pseudo-potential method within the density functional theory (DFT) framework. The effects of exchange and correlation were tested with the local density approximation (LDA) 12 and the generalized gradient approximation (GGA), with the Perdew-Burke-Ernzerhof functional (PBE) 13. Core electrons were described by the projector augmented wave method (PAW) 14,15, in which the 4d state of In and the 3d state of As were included as valence electrons. The computational code of the Vienna Ab Initio Simulation Package (VASP) was used 16,17. The electronic wave function was expanded in plane waves up to a cutoff energy of 520 eV. A gamma-centered grid of 8x8x8 k-point was used to sample the irreducible Brillouin zone. For the pseudo-potentials of In and As, the valence electrons in the states 5s2 4d10 5p1 and 4s2 3d10 4p3 , respectively, were considered. The thermal effects were analyzed using the quasi-harmonic Debye model, implemented in the Gibbs2 code 18. The Gibbs2 program requires energy-volume data obtained from first-principles calculations to obtain the Gibbs Free Energy G (V, P, T) and minimize G to establish the thermal EOS V (P, T). Details of this procedure were shown by the Code Developers (18, 19).
III. Results and discussion
A. Structural properties
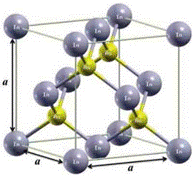
Fig. 1 shows the zinc-blende structure (ZB) of InAs. The unit cell consists of four In atoms and four As atoms and can be described by the lattice parameter a. In this structure, the anions of As are coordinated to four cations of In, forming AsIn4 tetrahedra with four As-In bonds, each In atom is shared by the four nearest tetrahedra.
In order to study the structural properties of InAs, we initially calculated the total energy of the conventional cell at different volumes, decreasing and increasing the experimental lattice parameter from -2.5 to 2.5 % 2,3 along the three perpendicular axes. The total energy versus volume curve shown in Fig. 2 was fitted to the Murnaghan equation of state 20:
Where B0 is the volumetric modulus, B'0 is its first derivative with respect to pressure, V0 is the equilibrium volume at zero temperature, and E0 is the equilibrium energy of the structure. The difference of the equilibrium energy of the LDA and GGA approximations is defined as: ∆E = ELDA-EGGA, if ∆E is negative, the LDA predicts the most stable structure; otherwise, if positive, the structure is more stable with the GGA. The calculated value for ∆E was approximately -5.20 eV, which indicates high structure stability with LDA.
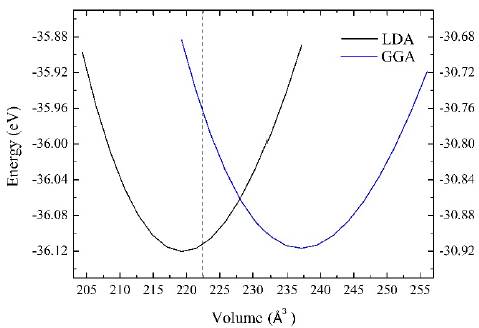
Fig. 2 Energy versus volume of InAs calculated with LDA and GGA. The experimental equilibrium volume is indicated by the vertical discontinuous line.
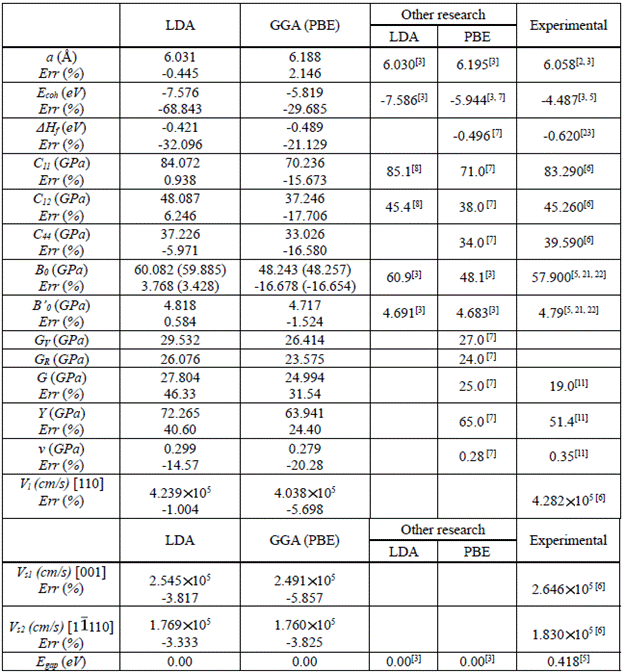
The lattice parameters, volumetric modulus and its derivative for the LDA and GGA are presented in Table 1, next to their respective experimental and theoretical results as reported by other authors. In this table, it can be seen that the values obtained by this research for the structural parameters (α, B0, B'0) approximate the theoretical 3 and experimental values previously reported 2,3,5,21,22. The LDA tends to underestimate the value of the lattice parameter α by 0.44 % with respect to the experimental value; while it overestimates the volumetric modulus by 3.42 %. In contrast to the LDA, the GGA corrects the underestimation of the lattice parameter and the overestimation of the volumetric module; however, it tends to overestimate and underestimate these values by ~ 2.14 % and ~ 16.65 % respectively. The values gathered from the derivative of the volumetric module are consistent with those reported experimentally and theoretically in the literature. The LDA tends to provide results that are closer to those reported experimentally, predicting more accurately the calculation of the structural parameters.
On the other hand, the cohesive energy (Ecoh) (by cation-anion pair) of InAs was determined using relation (2), where 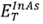 is the total energy per each cation-anion pair of the InAs compound,
is the total energy per each cation-anion pair of the InAs compound, 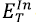 and
and 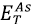 are the energies of the isolated atoms of In and As, respectively.
are the energies of the isolated atoms of In and As, respectively.
Table 1 shows that the results obtained for the cohesive energy with the LDA and the GGA are in agreement with those reported theoretically when using the same functional 3,7; however, it shows some discrepancy with the experimental results 3,5. This is due to the LDA and GGA limitations to reproduce the bonding energies between atoms, which are significantly underestimated.
In order to study the stability of InAs, the enthalpy of formation (∆Hf) (per cation-anion pair) was calculated using formula (3), where 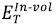 and
and 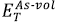 are the energies of the atoms of In and As determined in their cells. A positive (negative) value of ∆Hf represents an endothermic (exothermic) reaction. The InAs is a thermodynamically stable structure because it exhibits negative values of ∆Hf with both the LDA and the GGA approaches (Table 1), which agrees with the theoretical 7 and experimental 23 results reported in the literature.
are the energies of the atoms of In and As determined in their cells. A positive (negative) value of ∆Hf represents an endothermic (exothermic) reaction. The InAs is a thermodynamically stable structure because it exhibits negative values of ∆Hf with both the LDA and the GGA approaches (Table 1), which agrees with the theoretical 7 and experimental 23 results reported in the literature.
B. Elastic properties
The three independent elastic constants of the InAs (C11, C12 and C44) define the mechanical stability of the material, and are usually derived from the total energy calculations, representing the elastic properties of the crystal. The stability conditions for the cubic crystals are defined by (4).
The first condition is equivalent to C11>|C12|, and the first two imply that C11 > 0. The values of the elastic constants calculated with the LDA and the GGA (Table 1) satisfy these stability conditions. Therefore, the zinc-blende structure of the InAs is mechanically stable. When analyzing the results obtained using the two approximations, the sequence C11 > C12 > C44 is observed; this values are in line with those obtained experimentally 6 and theoretically 7,8. However, the LDA (GGA) overestimates (underestimate) the experimental values of C11 and C12 (C11, C12 and C44), while underestimating the value of C44.
From the results of the elastic constants, the anisotropy coefficient A of the InAs was determined using the relation (5) 24, which represents a measure of the anisotropy of the crystal. A perfectly isotropic material is one for which A has a value of 1, therefore, values smaller or greater than the unity represent a degree of anisotropy in the crystal. The calculated values for A were 0.48 for the LDA and 0.5 for the GGA, therefore, InAs is not perfectly isotropic in its elastic properties, which agrees with Ellaway et al.9 and Louail et al.10. These authors found that A is pressure independent and equal to 0.5 in the zinc-blende phase of the InAs.
If the aim is to calculate the isotropic elastic properties for polycrystalline materials, such as volumetric modulus (B0), shear modulus (G), Young's modulus (Y), and Poisson's ratio (v), when using the elastic constants of an anisotropic crystal, the averaged methods of Voigt-Reuss-Hill 25-28 are useful. For cubic systems, the volumetric modulus (B0) is the same for the averaged methods of Voigt and Reuss and is given by equation (6) 25-28:
The calculated value of B0 from the elastic constants had almost the same value as the one obtained from the adjustment of the Murnaghan equation of state (Table 1), which can be a good indicator of the reliability and accuracy of the elastic constants calculated for the InAs.
With the Voigt method, the shear modulus (G) in the cubic system is calculated using relation (7) 25-28, which provides maximum theoretical values for the shear modulus; whereas the Reuss method, given by (8) 25-28, obtains minimum theoretical values.
Generally, the arithmetic mean, G - (Gv + GR)/2, is taken as the estimate of the shear modulus; hence the value of G must be between those of Voigt and Reuss 26.
The Young's modulus (Y) and Poisson's ratio (v) can be expressed by (9) and (10) respectively.
The shear modulus (G), the Young's modulus (Y), and the Poisson's ratio (v) are important for engineering and technological applications. The first two provide a measure of the rigidity of the solid, that is, the higher the values of G and Y, the more rigid the material. The Poisson's ratio (v) is a measure of the crystal's shear strength and provides information about the characteristics of the binding forces. Values of v between 0.25 and 0.50 are given for solids with central forces 26. The calculated values of the shear modulus (G), the Young's modulus (Y) and the Poisson's ratio (v) are presented in Table 1, next to their respective theoretical (7) and experimental results 11. The predicted values of v are close to 0.3, indicating that the interatomic forces in the InAs are predominantly central forces. In this table, it can be observed that the values of the elastic properties mentioned above present some discrepancy with the experimental values. Similar results were reported by
Uesugi et al.25 when studying the elastic properties of AlLi. These authors assume that this behavior is due to the sensitivity of the elastic properties (except the volumetric modulus) of the actual polycrystalline materials, to the number of grains, and to the texture of the material. This was demonstrated experimentally by Kuriyama et al.29,30 by determining the Young's modulus of InLi. These authors showed that its value varied from 38.75 GPa to 67.8 GPa, which is about 75 % different; therefore, in the theoretical calculations, where elastic properties of monocrystalline crystals are predicted, this type of disagreement with the experiment is expected.
Table 1 Lattice parameter (a (Å)), cohesive energy (Ecoh) and enthalpy of formation (ΔHf) (per cation-anion pair), el astic constants (C11, C12 y C44), volumetric modulus B0 and its derivative B’0 shear modulus (G), Young’s modulus (Y), Poiss on’s ratio (v), spee d of a longitudinal wave in the direc tion [110] , spee d of a polarized shear wave in the direction [001] (V1), spee d of a polarized shear wave in the direc tion [110] ( Vs2 ) and band-gap energy Egap for InAs, calculated with LDA and GGA.
Due to the anisotropy of the InAs, the speed of sound in this material strongly depend on the direction of propagation. If the density (p) and elastic constants (C11, C12 and C44) of the cubic crystal are known, three independent speeds of sound can be calculated through relations (11-13) 31.
Where 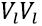 is the speed of a longitudinal wave in the direction (110),
is the speed of a longitudinal wave in the direction (110), 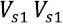 is the speed of a polarized shear wave in the direction (001), and
is the speed of a polarized shear wave in the direction (001), and 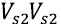 is the velocity of a polarized shear wave in the direction (110). The values for p were calculated with the LDA (5,747 g/ cm3) and the GGA (5,320 g/cm3); these results concur with the experimental value (5,680 g/cm3) reported by other authors 32. Table 1 presents the speeds of sound in the different directions of propagation along with their respective error percentages for each approximation with respect to the experimental values 6. The comparison between our calculations and the experiment indicates that the computational approach used to determine the vibrational properties of the system gives results consistent with the experimental values.
is the velocity of a polarized shear wave in the direction (110). The values for p were calculated with the LDA (5,747 g/ cm3) and the GGA (5,320 g/cm3); these results concur with the experimental value (5,680 g/cm3) reported by other authors 32. Table 1 presents the speeds of sound in the different directions of propagation along with their respective error percentages for each approximation with respect to the experimental values 6. The comparison between our calculations and the experiment indicates that the computational approach used to determine the vibrational properties of the system gives results consistent with the experimental values.
C. Electronic properties
Fig. 3 shows the partial states density of the InAs for each atomic orbital of the constituent elements, calculated with the LDA and the GGA. The zero energy has been placed at the Fermi level; below this level, the valence band (BV) is found between the energy range of -6 eV to 0 eV, formed with a higher contribution by electrons of the 4p-As states; the electrons of the 5p-In and 4d-In states have a lower contribution. The symmetrical distributions between the majority and minority spin regions show a nonmagnetic behavior in the InAs.
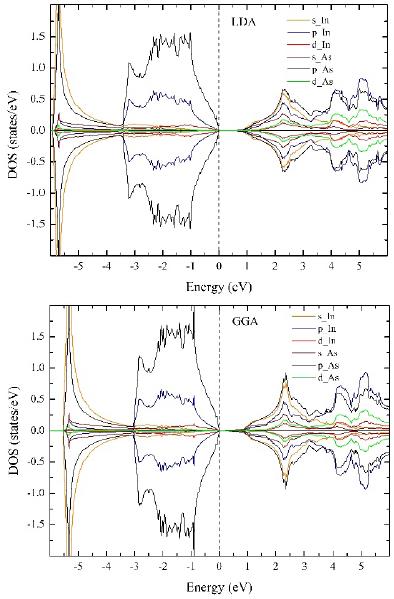
Fig. 3 Density of the partial states of the InAs compound, obtained with LDA (left) and GGA (right). The vertical discontinuous line indicates the Fermi level, which has been reduced to zero.
The calculated lattice parameter (α) is largely determined by the energy levels or layers of the outermost valence electrons. When the density of a state is calculated with the LDA, within the valence band, the states move toward lower energies and the orbitals near the Fermi level decrease considerably in height with respect to the band orbitals calculated with the GGA (Fig. 3), which could explain the decrease in the LDA lattice parameter in comparison to the GGA. Therefore, since the lattice parameter (α) in the LDA is of less value than in the GGA, the binding energy of the states of the valence electrons is overestimated, amplifying the coupling effects of the 4p-As and 5p-In orbitals. As a consequence of this strong coupling, there is an increase in the elastic properties obtained with the LDA when compared to the GGA (Table 1).
The conduction band (BC) is located above the Fermi level, and it receives a greater contribution from the 4p-As and 4s-In electrons and a smaller contribution from the other orbitals. The band-gap energy (Egap) is due to the interaction between the electrons that dominate the lower part of the conduction band and the electrons that dominate the upper part of the valence band, and its value was predicted by the aforementioned approximations (Table 1), which shows the tendency of the LDA and the GGA to underestimate the value of the band-gap energy in the semiconductors. Therefore, in figure 3, it is not possible to observe the semiconductor character of the InAs. Nevertheless, the Tran-Blaha-modified Becke-Johnson (TB-mBJ) potential 33 was used to correct the band-gap energy. TB-mBJ potential can give larger band-gap energy values than PBE or LDA functional, due to the fact that TB-mBJ is strictly an exchange-correlation potential. The band-gap energy value obtained is 0.28 eV, which is closer to the experimental data (0.418 eV) 5.
D. Thermal properties
The thermal properties of the InAs were calculated using the quasi-harmonic Debye model, in a temperature range from 0 to 1650 K, where this model is completely valid. In order to determine the thermal behavior of the compound, first-principles calculations were initially performed with the LDA and the GGA to obtain the energy-volume data, which are the inputs to the Gibbs2 program. Recently, the Gibbs2 code was used to study the thermal behavior of the compounds CSi2N4 and SCxYi-x34,35.
Figure 4 shows the volume (V), the volumetric modulus (B0), the Debye temperature (θD) and the heat capacity at constant volume (CV) as a function of the temperature and at 0 GPa of the InAs, calculated
with the entry data from the LDA and the GGA. In this figure, it can be observed that the volume (volumetric module) for each approximation increases (decreases) with an increase in temperature. However, it can be noted that the volume (volumetric modulus) is almost constant from 0 to 100 K and has a nonlinear increase (decreases) with the temperature for T > 100 K. It should be highlighted that the LDA (GGA) maintains the tendency to underestimate and overestimate (overestimate and underestimate) the volume and volumetric modulus, respectively, with the increase in temperature. On the other hand, the Debye temperature as a function of temperature and at 0 GPa remains unchanged with the increase in temperature in the range of 0 to about 100 K (Fig. 4c). When T > 100 K, the magnitude of θD decreases non-linearly, indicating the change in the vibration frequency of the particles with the temperature. Since θD is associated with the maximum crystal vibration frequency (ωD), according to relation (14) 36, it is expected for ù)D to be related to the oscillation frequencies of the InAs atoms, whose vibration frequencies are associated with the bonding forces, which in turn are related to the elastic properties, in particular with B0. Therefore, in observing the behavior of B0 with the temperature (Fig. 4b), a similar behavior was expected for 0d with a higher and near constant value at low temperatures (T <100 K), due to the rigidity of InAs within this temperature range; and lower at high temperatures (~ 1670 K for LDA and ~ 1150 K for PBE) where B0 tends to zero, implying that the material is softer.
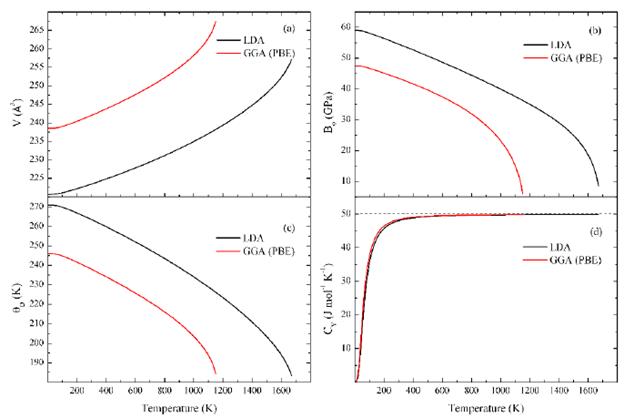
Fig. 4 Volume (V), volumetric modulus (ß0), Debye temperature (θD) and heat capacity at constant volume (Cv) as a function of temperature and at 0 GPa of the InAs.
The heat capacity at constant volume is another essential parameter used to describe the thermal properties of the InAs. At T = 0 K, the heat capacity tends to zero, and at low temperatures, it increases with T3 to approximately 200 K, due to the inharmonic approximation of the Debye model; then it gradually increases with the increase in temperature and converges to the constant limits of the Dulong-Petit law, where it does not depend on temperature (Fig. 4d). This is common for all solids at high temperatures.
IV. Conclusions
In the present research the structural, elastic, electronic and thermal properties of the InAs compound in its zinc-blende (ZB) phase were studied from first-principles calculations. Regarding the results of the structural parameters α, B0 and B'0, the LDA and the GGA generally agreed with the experimental data; however, the LDA tended to underestimate the value of the lattice parameter a, while overestimating the volumetric modulus and its derivative. On the other hand, the GGA approximation, even though corrected the underestimation (overestimation) of the lattice parameter α (volumetric module and its derivative), it tended to overestimate (underestimate) that value.
With respect to the elastic properties, the predicted elastic tests (C11, C12 and C44) were in line with those obtained experimentally and theoretically. Nevertheless, the shear modulus (G), the Young's modulus (Y) and the Poisson's ratio (v) showed some discrepancy with respect to the experimental values, although the obtained values were reasonable. The results obtained for the thermal properties with the Gibbs2 code, from the energy-volume data of the LDA and the GGA, showed that the volume (V), the volumetric modulus (B0), the Debye temperature (θD) and the heat capacity at constant volume ( CV ) are slightly sensitive as the temperature increases. According to the stability criteria and the negative value of the enthalpy of formation, the InAs is mechanically and thermodynamically stable. This work can be used as a future reference for theoretical and experimental studies based on InAs, since it covers the lack of data resulting from the few published reports on the thermal properties of this compound.