I. Introduction
The transport system is one of the crucial elements of the supply chain, and its management is one of the key activities of logistics. According to 1, the logistical costs can represent between 5 % and 18 % of the organization's sales volume. Among these costs, transport can represent between a third and two thirds of the total; therefore, one of the most important decisions regarding transport is the planning and programming of routes.
The decisions over programming distribution routes in their basic context have been mathematically modeled, using different approximations of the vehicle routing problem with capacities or VRP (Vehicle Routing Problem), which is considered a NP-hard problem 2. Some variants of the VRP include restrictions such as simultaneous delivery and collection, time windows, routes length, multiple warehouses, heterogeneous fleet, different objective functions, and stochastic elements, among others. All these variations give rise to multiple research problems in the area of transport in logistics. In particular, this article considers the variant of the VRP with heterogeneous fleet (HFVRP), in which each vehicle has assigned a load capacity, a maximum traveling time, a variable travelling cost, and a fixed acquisition cost. The main objective of the HFVRP is to determine the group of developed routes that minimize the total costs of the travelled distance.
The HFVRP considers that each customer must be attended by a unique vehicle that provides all their demands; that the sum of the route customers' demands must not exceed the capacity of the assigned vehicle; that the length of a route, contemplating the travel and service time, should not exceed the maximum time set per trip; that the available vehicles are limited; and finally, that each route begins and finishes in the warehouse. The study of the HFVRP is of big interest for the scientific community, because it allows solving a lot of real cases of programming routes for different companies 3.
This paper compares different granular neighborhoods (called granular because the search is restricted only to a part of the complete graph (G)) inside a Tabu Search algorithm (TS) for the vehicle routing problem with heterogeneous fleet (HFVRP). In particular, this study aimed at evaluating different operators to determine the best design of routes, considering the quality of the solution as a way of comparison. The main contribution of this article is the comparative analysis of the neighborhoods in algorithms of local search, efficient for solving route design problems such as the HFVRP. In addition to the studies by 4 and 5, the articles that compare the use of granular neighborhoods for vehicle routing problems are limited.
Section 2 reviews the literature on HFVRP, whereas section 3 details the general diagram of the algorithm and the neighborhoods used; finally, section 4 describes the computational results, and sections 5 lists the conclusions of the analysis.
II. Literature review
The vehicle routing problem with heterogeneous fleet has diverse variants, depending on whether the fleet is fixed or unlimited, and whether the costs are variable or fixed 6-7. Due to the computational complexity of the HFVRP, most of the technical proposals are framed within the heuristic and metaheuristics 8; nevertheless, some authors have proposed exact algorithms to resolve the HFVRP 9-11.
Heuristic algorithms based on Tabu Search (TS) for the HFVRP have been proposed in the literature 12-14. Brandão 12 introduced an algorithm based on TS that included strategic oscillation, perturbation procedure, and memory based on frequencies. Previously, the same author proposed a TS deterministic that used different heuristic procedures to generate the initial solution 13. Finally, an algorithm based on TS that included mutations and different procedures of local search was proposed by 14.
Diagrams of solution based on evolution strategies (ES) for the HFVRP have been developed by 15 and 16: 15 proposed a hybrid heuristic that combines genetic algorithms (AG) with a scatter search (SS); and 16 developed an algorithm designated approximated for the solution of the HFVRP. Additionally, hybrid algorithms to solve the HFVR have been proposed by 4,17-22: 17 proposed an algorithm of iterated local search (ILS), combined with a search of variable neighborhoods decline (VND) and a randomly neighborhood ordering (RVND); 18, an algorithm based on a variable neighborhood search (VNS) with several neighborhoods in the phase of local search; 19, an algorithm based on the development of a series of classical heuristics for the traditional VRP, followed by a local search (SDLS) and a TS; 20, an algorithm based on a procedure of adaptive memory with multi-start (multi-start AMP) and a modification of the traditional TS; 21, a method called threshold of acceptance (Threshold Accepting Approach), which adapts the procedure of simulated annealing (SA); and finally, 22 proposed a combination of the algorithm record-to-record with the method of the threshold of acceptance to solve the two variants of the HFVRP.
The comparative analysis developed in this study complements the state of the art, in terms of the efficiency of using granular neighborhoods within metaheuristics algorithms based on path. In the revised literature, with the exception of the work proposed by 3, there are no algorithms that apply the granular idea introduced by 4 for the HFVRP.
III. General diagram of the algorithm based in Tabu Search
In this section, we detail the principal aspects related to the proposed algorithm and the neighborhoods used in the comparative analysis for the HFVRP.
A. Granular space search
The concept of granularity, which was originally introduced by (4), consists in reducing the computation time when exploring neighborhoods, keeping solutions of high quality for heuristic algorithms based on local searches. In particular, the goal is to obtain "promising neighborhoods" (neighboring solutions of high quality) by means of using a list of candidates (incomplete graph G'), which contains the "short" arches of the complete graph G ; the arches incident to the warehouses, and the arches that belong to the best solutions found during the search 4. In this way, the local search is intelligently conducted, generating neighborhoods with the pertaining arches to the graph G'. The "short" arches are defined base on a threshold of granularity  . An arch can be defined as "short" if its distance is lower than
. An arch can be defined as "short" if its distance is lower than 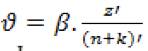 ; where
; where 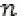 is the number of customers,
is the number of customers, 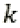 is the number of routes obtained in the initial solution of the algorithm,
is the number of routes obtained in the initial solution of the algorithm, 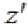 is the value of the objective function of the initial the vehicle routing problem with heterogeneous solution, and ß is a dynamic sparsification parameter that is adjusted during the search.
is the value of the objective function of the initial the vehicle routing problem with heterogeneous solution, and ß is a dynamic sparsification parameter that is adjusted during the search.
In procedures of intensification of the algorithm, β is small and near to zero; whereas in stages of diversification, ß takes higher values. Initially, the sparsification factor ß is adjusted to a small value ß0, and the resultant arches of the graph G' are stored in a matrix. If the best feasible solution has not improved after Iterß iterations, the sparsification factor ß is increased to a value ßf. Afterwards, the graph G' is recalculated and stored in a new structure.
In this way, the search begins again by Changeß iterations, beginning from the best feasible solution. Finally, the sparsification factor takes again its original value ß0 and the search continues, ßo, Iterß, ßf and Changeß are given parameters. Successful applications of the idea of granularity to different vehicle routing problems can be consulted in 23-30.
B. Algorithm based on Tabu Search
The proposed algorithm includes the generation of an initial solution through a heuristic procedure, and the improvement of such solution through TS, considering neighborhoods that follow the granularity idea mentioned above. Particularly, we considered four operators that generate granular neighborhoods, which will be detailed in section 3.3.
The pseudocode of the proposed algorithm is the following:
Pseudocode 1. Algorithm proposed.
In the pseudo code 1, we can observe that after generating the initial solution S0 a TS is applied for improving the routes, defining the size of the tabu list (magic) and the movements to be used (op). The magic parameter is randomly defined in a rank 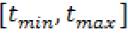 . The evaluation of neighborhoods begins with the generation of the list of candidates. Each granular neighborhood is obtained through the execution of simple movements (op) applied on the current solution (S’). Finally, during the search, the algorithm permanently updates both S* and the tabu list.
. The evaluation of neighborhoods begins with the generation of the list of candidates. Each granular neighborhood is obtained through the execution of simple movements (op) applied on the current solution (S’). Finally, during the search, the algorithm permanently updates both S* and the tabu list.
The initial solution is generated through a heuristic procedure (CW) based on the savings algorithm. The pseudo code of the procedure of initial solution (CW) is shown below:
Pseudocode 2. Procedure of Initial Solution CW.
The algorithm of initial solution allows the constant update of routes and allocation of trucks, attaining a balance between demand and capacity. The algorithm is an extension of the original procedure of the savings algorithm, applied to a vehicle routing problem with heterogeneous fleet, assigning trucks of elder to lower capacity.
C. Granular neighborhoods
Granular neighborhoods can be defined as enclosed feasible solutions generated by simple and promising G’ movements with the arches that belong to the graph G (See Section 3.1.). The computational time is drastically reduced, because the granular neighborhoods can be evaluated in less time than with an exhaustive local search, and without affecting the quality of the solution. The TS implemented is inclined to the use of these neighborhoods. In particular, a granular neighborhood (S") is generated through r - intercambios of arches of the solution S’’. In other words, to generate S’’ r arches of the current solution S’ are stirred up, replacing them with other r new arches that must be in the list of candidates. In this case, it is said that S" is a granular neighborhood of S'. According to 11, as the value of r increases, the computational time required to examine the neighborhoods increases as well. This characteristic is called neighborhood cardinality and can be measured as 0(nr). in this study, we have considered small values of (r ≤ 4). The four operations considered to generate granular neighborhoods were insertion, double insertion, exchange, and double exchange (24, 25).
IV. Computational results
A. Instances and resources used to execute the algorithm
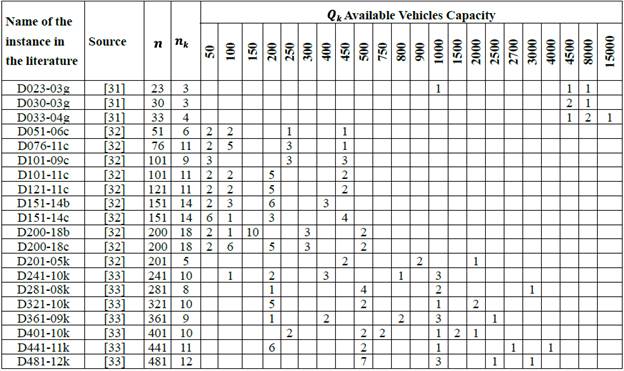
The proposed algorithm was executed on a group of instances of benchmarking obtained from the literature. Table 1 summarizes the main characteristics of the considered instances, taking into account n number of customers and nk number of available vehicles in the warehouse.
The algorithm was programmed in C++ using the compiler Dev-C++ version 4.9.9.2, in an environment Windows 7 Home Premium. The computational experiments were executed in an Intel Core i5 (2.3 GHz) with 4 GB of RAM.
B. Parameterization
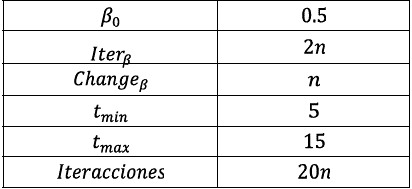
The success of the proposed algorithm directly depends on the precision in the parameter estimation; this is why extensive computational proofs were executed on the group of instances. Such experimentation determined that the critical parameter that directly affects the quality of the solution found by the granular neighborhoods is the value of ßf. In a first instance, to establish a rank of potential values of ßf, we used suggested values for similar problems 4. In this way, values of ßf were considered from 0.5 to 2.5 with increases of 0.25. According to 4, the quality of the solutions found for the routing problems is not directly proportional to the increase of the sparsification parameter ß, which is associated to a greater computational effort. We would expect that roughly selecting between 10 % and 20 % of the arches of the complete graph G, we could obtain solutions of high quality in a reduced computation time 4.
The value of the sparsification parameter ßf was adjusted in the analysis of every operator that generates the neighborhoods. In this way, a comparative analysis in terms of efficiency and quality of the solution was carried out. The other parameters were adjusted through the implementation of extensive computational proofs, fixing the operator that generates the solutions of best quality. Table 2 shows the parameter values obtained
without considering the parameter value ßf, which is analyzed in the following section.
C. Results
Several tests (180 runs) were performed to analyze each neighborhood. Indeed, 20 instances multiplied by 9 times the value of sparsification parameter ßf were executed. In this way, it was possible to determine the quality of the solutions found during the search and the most efficient operator in terms of the solution's quality. In the subsequent tables, the shaded values reflect an improvement of the objective function in relation to the initial solution S0.
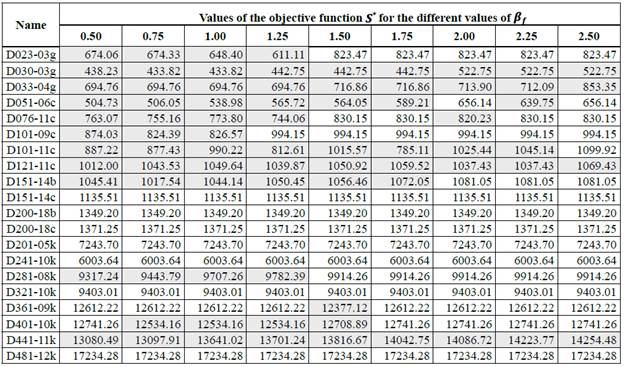
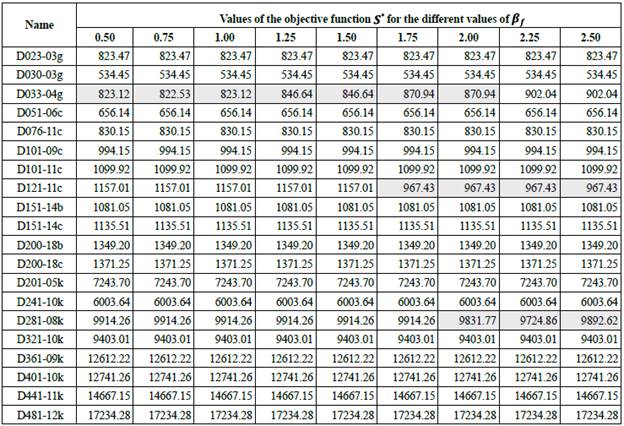
1) Neighborhood insertion: Table 3 shows the results obtained by the operator insertion for each possible value of ßf.
The greatest number of improvements was observed for ßf = 0.75 and ßf = 1.25 (Table 3). In particular, about 10 % and 20 % of the edges of the complete graph G were selected by considering these values of the parameter beta. The value of ßf was fixed to 0.75, based on the percentage of improvements in relation to the initial solution. By applying the neighborhood insertion, we obtained 12 improvements in the value of the objective function of the initial solution S0. Of this number of improvements, the greatest proportion was found in the two first subsets of instances.
2) Neighborhood double insertion: Table 4 shows the results obtained by the operator double insertion for each possible value of ßf.
The greatest number of improvements of the initial solution was obtained implementing the algorithm with ßf = 0.75. However, neighborhood insertion obtained better solutions than the double insertion (Table 6).
3) Neighborhood exchange: Table 5 shows the results obtained by the neighborhood exchange for each possible value of ßf.
In the case of the exchange operator, the number of improvements of the initial solution was minimum. The greatest number of improvements was seen when ßf = 2.0. Furthermore, the average improvement of the final solution was minimum in comparison with the results obtained by the neighborhood previously described (Table 5).
4) Double operator exchange: This neighborhood obtained the worst results for the problem and set of considered instances. In fact, the granular neighborhoods generated by this operator did not improve the initial solution. Therefore, this operator was not included in the comparative analysis of the different neighborhoods shown in Table 6.
D. Analysis of the results
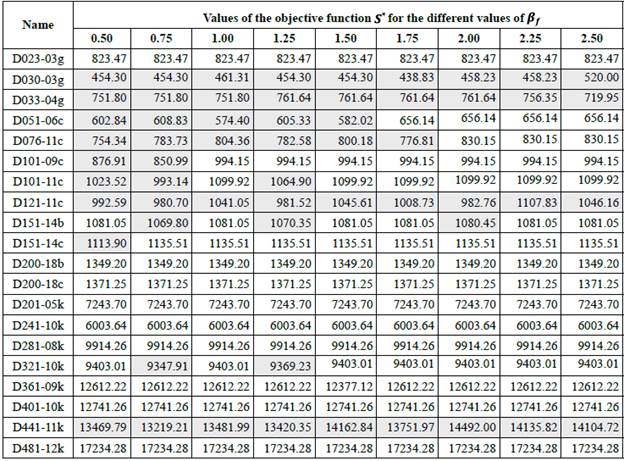
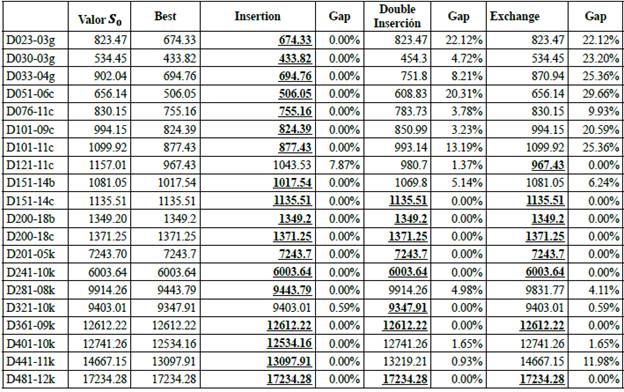
Table 6 summarizes the best results per operator, for the set of instances. Column "Best" shows the best results of the value of the objective function S* , obtained by the total of operators for each instance; whereas column "Gap" shows the percentage variation of the results found by each operator in relation to the value in column "Best". When the operator was able to find the best result (Best), the result is in bold and underlined.
The worst result for the set of selected HFVRP instances was obtained from the granular neighborhoods generated by the exchange operator (Table 6). However, this operator was able to find the best solution in 8 of 20 instances, and was the only operator able to find the best solution for the instance D101-11c.
The granular neighborhoods obtained through the double insertion operator allowed to obtain good results. In fact, the algorithm was able to find the best results in 8 of 20 instances. Likewise, the best result for the instance D321-10k was obtained through this operator (Table 6).
Finally, insertion was the neighborhood that allowed to reach the best results in 18 of 20 instances considered for the HFVRP. The reason for this could be that the insertion operator allows to easily readjust routes with a simple movement. On the other hand, the double insertion operator, when keeping the arch that connects to the two nodes that go to transfer to another route, generated too many infeasible granular neighborhoods that were not included by the algorithm. Finally, in the exchange neighborhood, four new edges must belong to the candidates list, which causes that a large quantity of neighborhoods are excluded by considering the granularity criteria. Obviously, it is important to mention that the efficiency of the operators in the generation of neighborhoods is determined by the quality of the initial solution S0 the value of the considered parameters, and the implementation form in the programming language.
v. conclusions and future investigations
In this article, we compared granular neighborhoods inside a Tabu Search (TS) for the vehicle routing problem with heterogeneous fleet and variable costs (HFVRP). In particular, the proposed algorithm is inclined to using granular neighborhoods and strategies of diversification and intensification based on the change of a dynamic sparsification parameter that is updated during the search. The TS proposal accepts only feasible solutions that are obtained through the different neighborhoods.
The comparative analysis was carried out considering a group of instances of benchmarking for the HFVRP. The computational experiments showed the efficiency and effectiveness of implementing the insertion neighborhood in the proposed algorithm.
The use of granular neighborhoods led to a substantial improvement in relation to the transport costs of the used fleet and the total distance travelled. The results obtained suggest that the implementation of the insertion neighborhood in algorithms of search based on path could be applied to other problems of similar distribution. We proposed the following future research:
Evaluation of the proposed methodology considering different objective functions, such as the minimization of the quantity of vehicles or the minimization of the environmental impact generated by the vehicles.
Consideration of fixed costs of using the vehicles in the objective function.
Generation of candidates lists that take into account the quantity of near customers, given selected customers. For each customer is considered that another is neighbor if it is inside the nearest customers no matter the distance that they are.
Inclusion of dynamic probabilistic operators that change during the search, privileging the neighborhoods that generate better solutions 34-35.