I. INTRODUCTION
The ammonia-water mixture (AWM) has been successfully used in many absorption refrigeration systems (ARS). AWM has played an important role in the use of heat pumps or as ARS applied or coupled to diverse external systems, such as distillation towers [1], Kalina cycles, which have higher pressures than a conventional system [2,3], air conditioning systems, and combustion air cooling for gas turbines and streams in extractive industries such as coal and petroleum [4]. Most of the design and analysis of ARS until a little after the first half of the last century was based on graphical predictions. However, the range of pressures was small, and based only on few experimental data points and theoretical-empirical deductions [5,6,7].
The precise thermodynamic properties of the ammonia-water mixture are very important for the calculations in the design of ARS equipment and the prediction of their behavior; this also applies to the operation of existing systems and their possible improvements. In the past few decades, the analysis of these systems has covered their performance based on both the first and the second law of thermodynamics; this analysis involves the use of the specific entropy value, which is fundamental to improve the prediction and optimization of cycle performance [1,3,8,42]. The more than forty-five published methods for predicting the thermodynamic properties of AWMs have been classified into seven main groups according to Thorin et al. [9]. In these groups, there are combinations of cubic equations of state, excess Gibbs energy, corresponding states, perturbation theory, group contributions, and polynomial functions. Other developed methods are the Helmholtz free energy [14], the PC-SAFT equation [26], neural networks [19,27], and others that mix two or more groups [10-13,15-18,20-25,28-30].
Due to the above, in most cases, the precise estimation of the water concentration in the generator exit (desorber and rectifier) results in over or under design of these components [5,31]. The disadvantage of some models is the restricted range over which they are valid, and in other cases is the lack of entropy prediction [32]. Currently, due to the need of predicting exergy balances, the cubic equations of state, which are incorporated in commercial process simulators for such systems analyses, have been used [1,8]. However, because the mixture in question is highly non-ideal, these equations of state lack the necessary adjustments to accurately predict its properties at ammonia concentrations close to unity. For this reason, many researchers have taken on the task of modifying or generating specialized equations. Nevertheless, there are few models with a wide range of applicability [9,26,33].
Here, an ARS has been evaluated according to both the first and the second law of thermodynamics, and the energy and irreversibility, with the aim of finding differences between three mathematical models for predicting thermodynamic properties [14,18,35]. A base case from the literature [34], in which the thermodynamic properties were calculated via a mathematical model based on Gibbs free energy, was employed to compared to the results obtained from the three methods herein considered.
II. METHODOLOGY
We used three different methods to obtain the thermodynamic properties of the operating conditions given in the proposed base case [34]. M1, a model developed by Ibrahim and Klein [35], is implemented in the commercial program Engineering Equation Solver (EES); M2, proposed by Tillner-Roth and Friend [14], is implemented in REFPROP v.8.0 developed by the National Institute of Standards and Technology (NIST); and M3, proposed by Xu and Goswami [18], was developed from work by Ibrahim and Klein, El-Sayed and Tribus, and Ziegler and Trepp [35-38,40]. To carry out this analysis, the latter methodology [18] was programmed and validated [5,12,39,43].
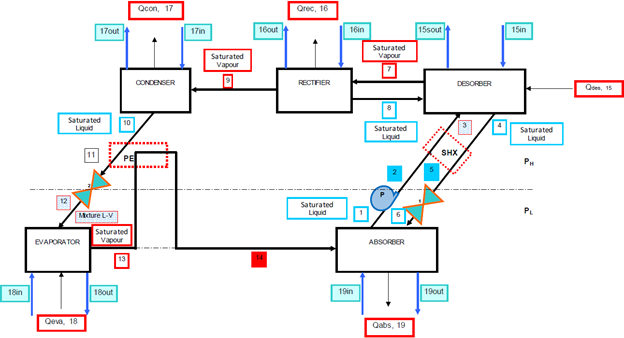
The analysed ARS [34] consisted of a simple single effect ammonia-water cycle with a solution heat exchanger and a pre-cooler (super heater), which had fourteen streams and ten components (Fig. 1).
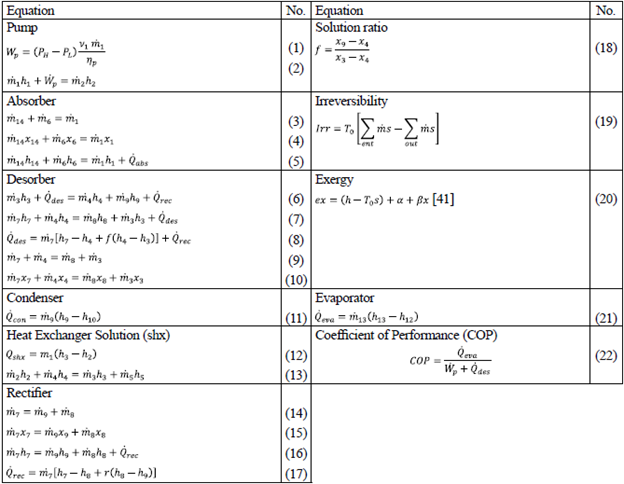
The initial conditions and mass and energy balance equations for the corresponding analyses under the first and second laws of thermodynamics are given in tables 1 and 2.
Table 1 Considerations For The Analyses With The Three Models Employed
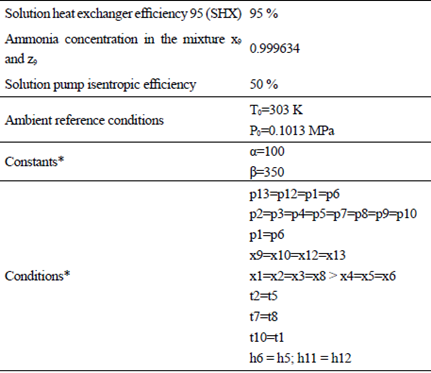
*Where α and β are random constants; x is the mass fraction of ammonia in the corresponding stream [41].
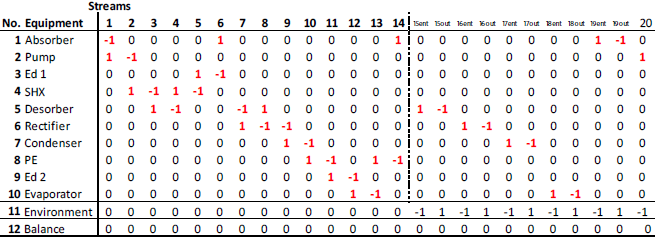
The matrix shown in Fig. 2 was used to solve the system mass, energy and exergy balances with vectors corresponding to the streams in the system.
III. RESULTS AND DISCUSSION
A. First law analysis
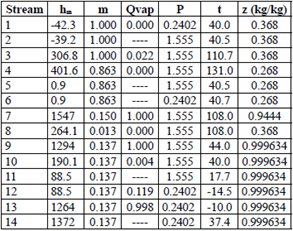
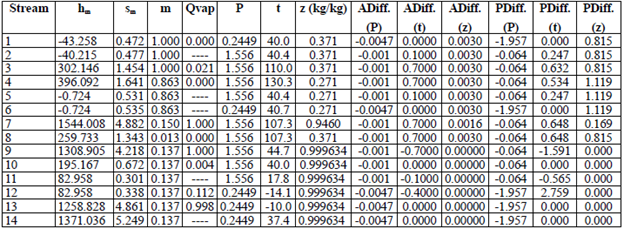
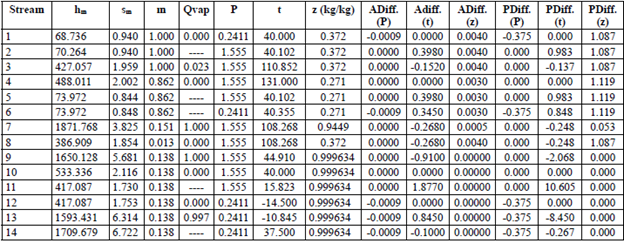
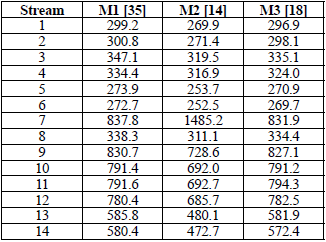
Tables 3 through 6 show the thermodynamic properties for each stream. Table 3 reports the data from the base case, which were compared to the other models: M1, M2 and M3. The data obtained from Model 1 (EES) showed differences with respect to the base case; however, no property (P, t, z) differed by more than 3 % (Table 4). Table 5 shows the data obtained using M2, implemented in the REFPROP NIST software.
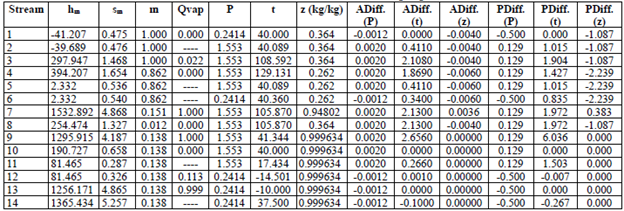
The differences in hm and sm compared to the base case and M1 (Table 5) are mainly due to the fact that the reference properties from which the predictive model works are different [33]; nonetheless, when these properties (P, t, z) were compared, the percentage difference in pressure reached more than 10 %. For M3 (Table 6), the values were very similar to the base case and M1. Notwithstanding, there were differences in enthalpy and entropy in relation to M2 due to the reasons given above. The maximum percentage difference in P, t and z was in pressure, which was 6.036 %. The differences in temperature and concentration did not exceed 3 % in any of the models. M1, M2 and M3 have an extra column that corresponds to the entropy vector values (sm).
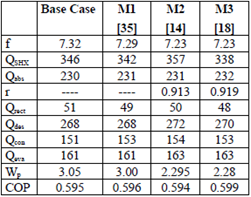
The results from the first law analysis of the system showed slight variations compared to the base case (Table 7). The overall differences were of little significance, even though the solution heat exchanger and the solution pump showed greater variations. In the case of the solution pump, the simulations using REFPROP and M3 had the least difference between each other, compared with their differences from the base case. For the solution heat exchanger, the differences with respect to the base case were the lowest for the EES method and M3, compared to the results with REFPROP. Despite the differences among the various models, the coefficient of performance was substantially the same for all models; hence, any of the models is adequate for first law analysis of the system.
B. Second law analysis
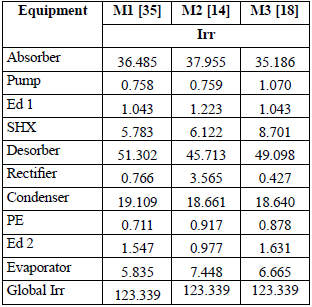
The irreversibility analysis did not include the base case since no entropy values were reported (Table 8).
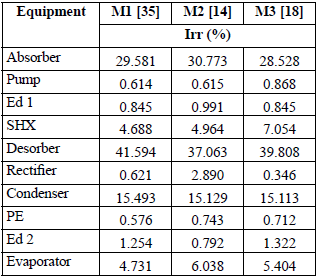
Table 9 shows the size of the irreversibilities (Irr) for each component (kW), while Table 10 gives the representativity of these irreversibilities as a percentage for each component. All the models gave the same total irreversibility (Overall Irr = 123.339 kW). However, the solution heat exchanger, the desorber, the rectifier and to a lesser degree the absorber were remarkable, since for them there were significant differences among the models and the resulting values of exergy loss. This is due to the differences in the specific entropy calculated by each model in the vapor phase when the ammonia concentration was close to unity. For the other components, the results were very similar and, therefore, they can be considered generally acceptable for a second law analysis and design decisions. The components with the greatest exergy destruction were the desorber, followed by the absorber and the condenser.
IV. CONCLUSIONS
The values of the properties calculated by the three methods (M1, M2 and M3) compared to the base case showed significant differences for only some of the streams, and particularly for the pressure prediction in the case of nearly pure ammonia in the vapour phase. However, when the overall system heat and mass balances were analysed, the differences were small, and in particular, the coefficient of performance was reasonably consistent. When the second law analysis was considered, differences were found in the exergy values for the process streams calculated by the models used in this study. The orders of magnitude of the percentage contributions to the overall irreversibility of the system were consistent among models; that is, desorber, absorber, and condenser were the components with the greatest irreversibilities. Notwithstanding, the observed differences in the overall irreversibility were the same in all cases.