I. INTRODUCTION
The design of tubes with extended surface has been important due to the necessity of cooling electronic devices and/or engines through free convection [1,2,3], and handling oxidation reactions based on heat transfer in hybrid vehicles [4]. The research in this area has allowed avoiding heating problems, and the subsequent potential failures or mechanical problems [1]. This research is based on the analysis of finite elements, to study the thermal-mechanical behavior, through simulations of continue thermal variations and energy absorption [5,6].Likewise, artificial neural networks have been used to observe the times in convection processes in plain but small diameter tubes [7].
The analysis of finite elements requires knowing the materials used to construct the tubes, such as graphite and carbon used for nanotubes of different diameters [1,8], brass [6] and its alloys [9], reinforced plastic fiber [5], which has good thermal properties and mechanical strength, and iron alloys with chrome [10]. Therefore, the relationships between materials and design of mechanical parts have improved the performance in industrial mechanisms [4,11,12]; for example, new structural designs, such as thin origami tubes have been created to improve energy absorption [6] and heat transfer (e.g., Vipertex tubes) [13], and to optimize extended surfaces that reduce costs and improve heat flow [9]. Another variation in the design of extended surfaces is found on how the toothed fins are handled, that is, the height, thickness, and number of fins vary to evaluate the heat transfer flow between the environment and the fast reactors [10]; additionally, internal fins can be used to perform high-fast cooling [14,15] in the same way ultrasonic vibrations are used [16].
The graphical concept of fractal geometry has been introduced to the design of physical structure of mechanical parts to take advantage, in the industrial process, of the structures observed in nature [17]; for example, to evaluate supports and their structural strength [18,19], and to interpret porous microstructures to improve the thermal conductivity efficiency of electrical circuits [20].
In this paper, we begin by describing the methodology used to design the tubes with fractal extended surfaces, then explain the Koch snowflake and Cesaro curve as the fractal structures that were taken into account for the design, and then detail the flow analysis with finite elements. After obtaining a clear relation between the extended surfaces of a tube and its heat flow variation, we show the results of subjecting the tube to different internal and external temperatures. Finally, we analyze the results and present the conclusions obtained from the heat transfer analysis.
II. METHODOLOGY
In order to design and analyze the tube with fractal extended geometry, first, we compared the fractal geometries similar to the longitudinal surfaces (Fig. 1). These types of tubes are commonly used in applications such as air coolers, dry coolers, evaporators, and condensers that transfer energy from a main liquid or refrigerant medium to the air [21]. The longitudinal surfaces are fins elaborated in thin aluminum plates, considered good conductors because they increase the heat transfer by increasing the main tube surface.
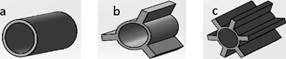
FIG. 1 Tube surfaces: a) Main smooth surface tube; b) extended surface tube with three longitudinal fins; c) extended surface tube with six longitudinal fins.
The heat transfer analysis for this kind of tubes corresponds to observing the thermal interaction between the fluid inside the tube and the external medium surrounding the extended surface. First, equation (1) calculates the thermal difference (Θ) between the fluid surrounding the fins (Tc) and the specific point temperature over the fin (t).
Then, equation (2) takes into account the variation of the temperature along the height of the fin 
Equation (3) estimates the heat (Q) through the cross section by conduction, where a x is the cross-section area of the fin, and k is the conductivity thermal coefficient. According to Newton's law, it is possible to improve the heat exchange to increase the a x.
To obtain the heat variation with respect to the height (dQ/dl), the derivate of equation (3) is obtained, resulting in equation (4).
We used the geometry of the Koch snowflake to increase surface, and thus improve the heat transfer of a tube with conventional extended surface. The Koch snowflake sketch was built up to generation 12 to preserve the self-similarity configuration from the location of three copies of the Koch curve (Fig. 2). The Koch curve can be found as the division of three same parts of a line, with the middle line being replaced by an equilateral triangle; this process is repeated for each generation, at each segment obtained in the previous generation [22].
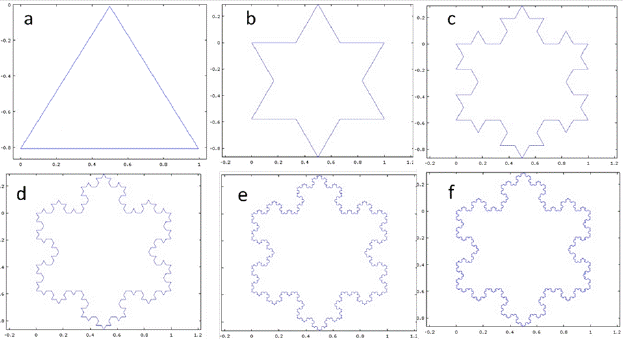
FIG. 2 Koch snowflake fractal geometry: a) Germen, b) Generation 1 c) Generation 2, d) Generation 3, e) Generation 4, and f) Generation 6.
Equation (5) calculates the length of each line segment (L) at each generation (n); here, the initial length (L 0) corresponds to the lengths of the sides of the initial equilateral triangle.
After sketching the Koch snowflake, we initiated the CAD design of the tube with extended fractal surface (Fig. 3). The elaboration of this design was limited to the sketch of the third generation, due to the increase of the tube surface, which might decrease the heat transfer.

FIG. 3 CAD design of the tube with Koch snowflake extended surface: a) Initial generation, b) Generation 1, c)
The Cesaro curve is considered a similar geometry to the Koch snowflake, with big affinities to extended surfaces of longitudinal fins (Fig. 4). To obtain the Cesaro curve, equation (6) is necessary, as well as the following steps: 1) draw a line with length L0, 2) draw a line from the middle of the previous line, and 3) build an isosceles triangle with length L. Therefore, to join the Cesaro curve as an extended surface of the tube for heat exchangers, we start by using a hexagon where each side has a length Lo and the maximum fractal geometry iteration correspond to the third generation.
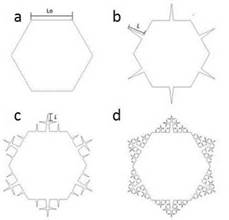
FIG. 4 Cesaro curve geometry: a) Initial generation, b) Generation 1, c) Generation 2, and d) Generation 3.
Similarly, we elaborated the CAD design by adding the Cesaro curve (Fig. 5), where the tube with each generation as an extended surface can be appreciated.
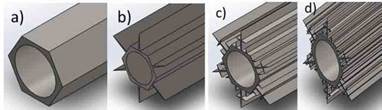
FIG. 5 CAD design of the tube with Cesaro curve as extended surface for heat transfer: a) Initial generation, b) Generation 1, c) Generation 2, and d) Generation 3.
We used SolidWorks software to design each CAD, and ANSYS software to initiate CAE finite element analysis, in order to observe the variation of heat transfer inside the tube, and the interaction between the tube with extended surface and the environment. For the simulations, we adjusted the air flow to room temperature (22 °C), indicating an internal temperature of 200 °C, and assigned to the tube a copper material with thermal conductivity of 400 W/(m°C).
III. RESULTS
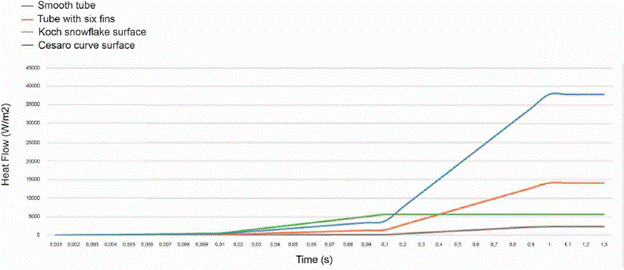
Figure 6 shows the results obtained from the analysis of finite elements, particularly the behavior of the heat flow (W/m2) in the different types of tubes.
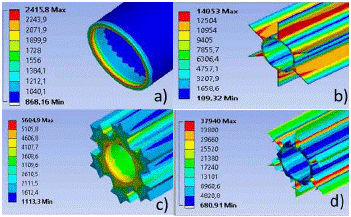
FIG. 6 Thermal flux behavior: a) smooth tube, b) tube with extended surface of six longitudinal fins, c) tube with extended surface of Koch snowflake of second generation, and d) tube with extended surface with the Cesaro curve of second generation.
Figure 7 explains the results better, showing the variation of the heat flow in each of the tubes, arranged for thermal transfer.
IV. DISCUSSION
The results showed that the tube with extended surface of the Cesaro curve increased the heat transfer from the inside of the tube to its surroundings; this is because the contact area of the external fluids increased, and the tube's geometry facilitated the turbulence that favors the early change of the internal and external temperatures of the tube. Although the tube with extended surface with the Koch snowflake did not surpass the heat transfer of a tube with extended surface of longitudinal fins, it would be useful when a faster heat transfer is required.
V. CONCLUSIONS
This study showed that it is possible both to integrate fractal geometries to the field of mechanical engineering, specifically to the area of heat transfer, and to make viable designs with the support of CAD and CAE tools. Likewise, the results of this study serve as foundations to continue the research in this area, oriented toward the application in devices that exchange heat at industrial, automotive, and household level, such as heaters, boilers, and radiators; and with the goal of offering to the market new devices able to handle high temperature in short times.