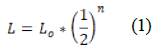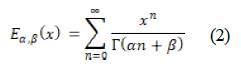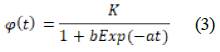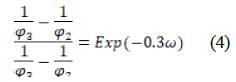I. INTRODUCTION
A. Fractal geometry and its applications
Fractal geometries are those geometric relationships that are responsible for interpreting and representing the various forms of nature [2]; in addition, they allow measuring the irregularity of the objects, the natural processes and the physiology of the human body [3]. Among the most representative fractal geometries are the Koch snowflake, the rug of Sierpinski and the Cesàro curve [4]. Similarly, the structure of irregular objects (e.g., the organs of the human body) [5], the micro-organisms, the growth of normal and carcinogenic cells [6], and the cerebral blood flow in people with Alzheimer's have been analyzed. Previous research has been able to develop tissues from biocompatible materials from fractal biomimeticas geometries, which seek to obtain tissues similar to those of the living organisms [7].
In geology, calculations aimed at determining the level of a geological fault in an area have been done from the fractal dimension [2,8]; likewise, geo-forms such as planets or drainage basins have been analyzed [9]. In engineering, nano-level antennas have been developed with fractal geometries [10,11]. The fractal exponent of Hurst has been proposed as an application in mechanical engineering; it allows analyzing signals in the process of machining to avoid system failures [12,13] and visualizing the behavior of the scaling of fracture surfaces in composite materials, using fractal fractures [14]. In mathematics, software has been developed as a winch with fractal foundation, to identify numerical patterns and improve the transition from arithmetic to algebra [15].
B. Heat exchangers and heat transfer
The industry has developed mechanisms that improve heat transfer, like designing stoves with a combination of materials that reduce heat loss [16]. Other variable considered is the convective coefficient, which facilitates the exchange of temperature during heating, cooling or freezing [17]. An example of such mechanisms is the one developed for minimizing the entropy in the heat transfer of electrical circuits, which raises the need to design cooling devices to avoid possible damages to the elements that make up the circuit [18]. Therefore, it is necessary to continue studying heat transfer in elements such as tubes, from their length to the number of Reynolds, for adjusting the pipe bench [19]. In this sense, software that exposes the dynamics and control of heat exchangers of tubes and armor, of interactive use between the student and the same one, have been developed [20].
Implementing combustion gases to heat air is one of the commonly used methods [21]; in other cases, various pipe configurations have been developed to improve the storage of fluids at high temperatures. A main element in the heat transfer process is the extended surface tube, which generated great interest in the field of mathematical modeling to improve the efficiency of heat generation [22]. In this case, the type of fin determines the characteristics of the flow and the resulting transfer coefficient, whose studies have focused on numerical analyses from commercial software [23].
In this study, we first explain the methodology used to design and analyze the extended surface of the Cesàro curve for tubes arranged for heat exchangers. In this case, the piece was developed with the computer-aided design (CAD) SolidWorks, to conduct the analysis with the finite elements computeraided engineering (CAE) ANSYS. Second, we compare the commercial longitudinal extended surface tube with the results obtained, showing that the flow in the heat transfer process is better.
II. METHODOLOGY
The design of the tube with extended fractal tree surface began by elaborating a sketch (Fig. 1). To perform the geometry that corresponds to the Cesàro curve, a hexagon was made, assigning its function as base geometry, then the procedure was implemented to obtain a fractal tree, where the idea was to draw the base of the tree and in each iteration replicate the tree with its branches on its corresponding scales [24].
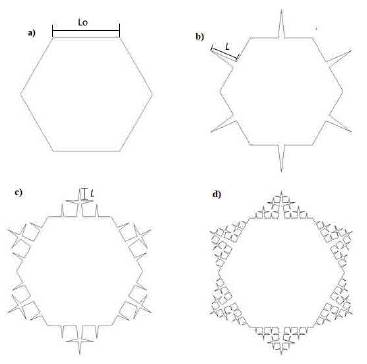
FIG. 1 Design and elaboration of fractal tree to implement on extended surfaces, where a) is the base geometry, b) is associated to each side of the base of the tree, c) is placed at the base and the branches and d) is a replica of the base of tree the branches on a smaller scale.
To understand better how to obtain each fin of the tube with the Cesaro curve, we considered equation (1), which indicates the length corresponding to each branch from the initial length of the fin (L) and the iteration to be replicated.
After making the sketch to implement the fractal tree on the extended surface of a tube for heat exchangers, we designed the tube with the computer-aided design (CAD) SolidWorks (Fig. 2). The initial design of the tube with extended surface allowed performing the analysis by finite elements with the computer-aided engineering (CAE) ANSYS, to evaluate the rate of heat transfer and its behavior.

FIG. 2 CAD design of the tubes for the analysis by finite elements of the heat transfer, where each of the figures correspond to the solid developed from the proposed sketches.
The analysis was carried out by finite elements, where it was necessary to enter and adjust the internal surface at a temperature of 200 °C, assigning to the copper tube a coefficient of thermal conductivity of400 W/(M * °C), then a room temperature (22 °C) was assigned with a thermal convection coefficient of 5 W/(M2* °C). The development of CAE analysis tools, from logistical models, can be estimated with the so-called fractional or fractional model [25], of the type Mittag-Leffler generalized, developed from the equation (2), where 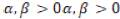 .
.
When α=β=1, you get a function Exp(x)=e 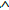 x, which leads to the conclusion that the generalized function of Mittag-Leffler resembles the widespread exponential function; therefore, it was possible to estimate the generalized logistic models [26]. To conduct a mathematical approximation, the model of the smooth tube was adjusted with equation (3), starting from the conditions suggested in [27].
x, which leads to the conclusion that the generalized function of Mittag-Leffler resembles the widespread exponential function; therefore, it was possible to estimate the generalized logistic models [26]. To conduct a mathematical approximation, the model of the smooth tube was adjusted with equation (3), starting from the conditions suggested in [27].
III. RESULTS
After designing the tubes to be evaluated, we analyzed the Steady State Thermal in ANSYS, which allows evaluating the temperature variation and heat flow by convection, conduction and radiation between different media, like solids and fluids. For this case, we obtained the thermal flow or heat transfer that is shown in Fig. 3.
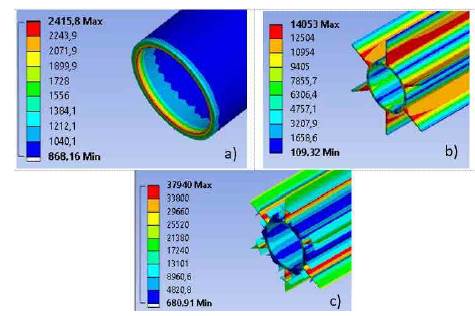
FIG. 3 Thermal flow between a fluid with a temperature of 200 °C in the interior of the tube and 22 °C on the outside, posing the analysis for a) smooth tube, b) extended surface tube of longitudinal fins, c) tube with extended surface of longitudinal fractal tree.
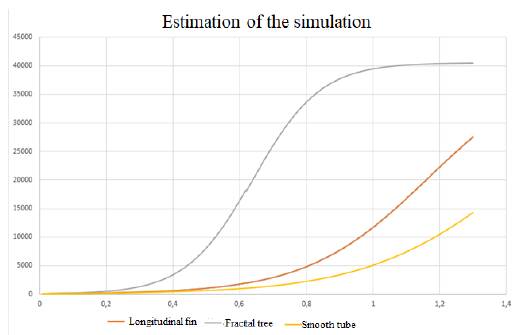
Fig. 4 shows that the finned tube extended with fractal tree geometry presents a better behavior, suggesting that a greater heat flux may be possible. For the comparison shown in Fig. 4, we took three equally spaced values of the simulation: 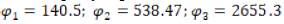
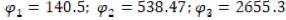 which were replaced in equation (4) to get
which were replaced in equation (4) to get 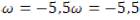 .
.
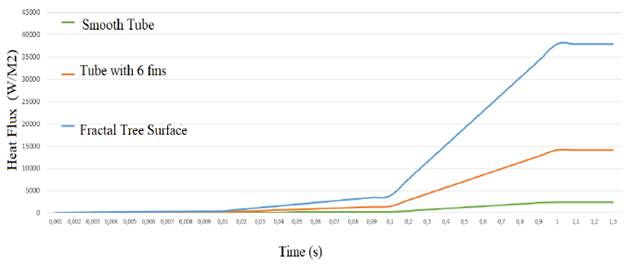
FIG. 4 Heat flow comparison between the smooth tube (green line), the tube with an area of longitudinal fins (orange line), and the tube with an extended surface with fractal tree (blue line).
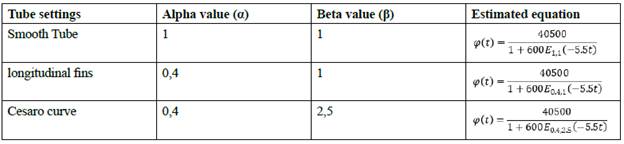
Subsequently, to obtain the parameters for the other extended surfaces, we considered the data shown in Table 1.
The results of graphing 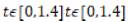 are shown in Fig. 5.
are shown in Fig. 5.
IV. DISCUSSION
The results obtained lead us to conclude that implementing fractal tree as an extended surface in tubes arranged for heat exchangers allows a greater transfer of heat between the fluid in the inside and the outside of the tube. The evaluated extended surface increases the contact surface and expands the edges of the extended surface, which facilitates the heat exchange, because it improves the turbulence of the fluid and thus the transfer of heat.
V. CONCLUSIONS
Implementing fractal geometries of mechanic areas has generated great interest for developing materials, and improving their internal structure to enhance mechanical properties such as maximum effort and durability. In this case, by implementing the fractal tree at the macro level, as an extended surface, it is possible to improve heat transfer, which can favor thermal processes in heat exchangers in capacitors and refrigerants, among others.
As a future work we are working on assigning application designs to industrial and domestic devices, which will allow demonstrating real-time behavior to meet the three main design lines: CAD, finite element analysis and item production. This process is proposed with the aim of reaching the market and increasing the handling capacity of high and low temperatures depending on their application.