I. Introducción
En este artículo se aborda el problema del pronóstico de la demanda de asignaturas, que se asemeja en gran medida al problema genérico del pronóstico de la demanda de un servicio. Sin embargo, existen una serie de diferencias interesantes entre ambos problemas. El problema del pronóstico de la demanda de asignaturas ocurre en el contexto de las universidades y centros educativos en donde los alumnos solicitan inscribirse en un conjunto de materias cada uno de ellos y se requiere conocer de antemano un estimado de la demanda para poder presentar una cantidad apropiada de oferta de asignaturas.
Este problema se considera relevante, ya que para poder realizar una planeación acertada o relativamente acertada se requiere tener la mejor aproximación de los datos reales necesarios para poder planificar el próximo período. Esto impacta, no solo a las personas que desarrollan los horarios y apartan cada una de las aulas y laboratorios, sino a la parte administrativa de los centros educativos; que se encarga del apartado del recurso económico requerido para pagar a los profesores contratados y en caso de ser necesario, realizar las convocatorias necesarias para solicitar nuevos profesores, siendo este último un proceso que requiere de mucha anticipación al nuevo período de clases.
En este contexto la planeación del próximo período incluye, y no está limitado a asignar los profesores que impartirán cada asignatura, definir los horarios de clase, definir las aulas/laboratorios a utilizar, identificar la necesidad de actualización de profesores e identificar la necesidad de realizar nuevas contrataciones como ya se describió anteriormente.
Además de lo anterior, el mayor problema radica en cumplir todas las restricciones de la planeación, tal es el caso de evitar asignar dos asignaturas diferentes al mismo grupo de alumnos en la misma hora, o asignar a dos grupos de alumnos diferentes en la misma aula a la misma hora, o asignar al mismo profesor a dos asignaturas diferentes a la misma hora, por mencionar algunas de ellas.
El objetivo final del software propuesto es el de tener un pronóstico de la demanda de los estudiantes a asignaturas lo más cercano posible a la realidad. Considerando que existe una seriación de las asignaturas y que los alumnos no pueden solicitar asignaturas indiscriminadamente.
En este sentido, existe una forma de calcular la demanda futura de asignatura ai,t +1, esto es una asignatura a de una seriación i en el siguiente período t+1 como se observa en (1):
Donde: aprobación(ai −1,t ) representa la cantidad total de alumnos que aprobarán la asignatura subsecuente en la seriación de materias, reprobación(ai,t ) representa la cantidad total de alumnos que reprobarán la asignatura a la que se le desea calcular la demanda (ai ), y alumnos_en_espera(ai ) representa aquellos alumnos que quisieron tomar la asignatura ai pero no pudieron inscribirse en el período actual. Todos estos datos son datos obtenidos a partir del período actual (t).
Por otra parte, solamente se puede conocer el número de alumnos_en_espera(ai ), mientras que para aprobación(ai −1,t ) y reprobación(ai,t ) se requiere de un porcentaje estimado de aprobación, ya que el porcentaje estimado de reprobación se puede obtener del complemento del anterior (100 - aprobación(ai −1,t )). De tal forma que se puede utilizar un porcentaje fijo generalizado de aprobación (75%, 80%, 85%, etc.) para todas las asignaturas o utilizar alguna otra técnica para realizar un pronóstico más ajustada a la realidad, dado que es difícil que se produzca el mismo índice de aprobación para todas las materias.
II. Propuesta de solución
En este artículo se plantea un proyecto que tiene como principal objetivo el desarrollo de un software para el pronóstico de la demanda de asignaturas basado en el análisis de índices de aprobación históricos. Chambers, Mullick & Smith [1] presentan un análisis de los métodos de pronóstico disponibles y la forma en que estos son seleccionados dependiendo del contexto, la disponibilidad de los datos y su relevancia, el nivel de precisión deseado y el tiempo requerido para realizar el pronóstico entre otros.
Por otra parte, Armstrong [2] recomienda el uso de métodos cuantitativos sobre métodos de criterio siempre y cuando se tengan suficientes datos, esto es un requisito para todos los trabajos relativos a métodos del pronóstico cuantitativos presentados en este artículo. En este sentido, en Bailey & Gupta [3] se recomienda tener ocho observaciones como mínimo para considerar los métodos cuantitativos como una alternativa que pueda proporcionar mejoras sobre los métodos de criterio. Además de lo anterior, los métodos cuantitativos son más propensos a mostrar mejor desempeño cuando se presentan grandes cambios en los datos. En términos generales, si se tienen suficientes datos es preferible utilizar un método cuantitativo.
Una vez decididos en utilizar métodos cuantitativos se recomienda utilizar métodos causales en vez de métodos simples, especialmente si se esperan grandes cambios en el pronóstico. Sin embargo, también se establece el principio de parsimonia en el que se establece que son preferibles los métodos simples sobre métodos más complejos a menos de que exista evidencia sustancial que indique que la complejidad del método ayude al pronóstico [4].
Dadas las características del estudio a realizar en este trabajo consideramos el uso de análisis cuantitativos, y como es recomendado, modelos causales. Como parte inicial de este trabajo de investigación, se presenta un análisis y estudio del desempeño de un modelo estadístico contra un modelo causal con el fin de presentar evidencia en contra del principio de parsimonia.
A. Datos
Los datos utilizados en este trabajo son datos reales tomados de la Facultad de Ingeniería de la Universidad Autónoma de Tamaulipas y se planea que sean datos que sirvan tanto para el método estadístico como para el método causal.
De forma general, antes de realizar cualquier proceso de análisis de datos es recomendable realizar un preprocesamiento el cual incluye la selección, depuración y normalización de datos entre otros procesos. En este trabajo se realizarán los procesos de selección y depuración para conservar los datos relevantes las causas de los resultados presentados y evitar incluir datos que podrían introducir información irrelevante y perjudicar el desempeño de los métodos a utilizar.
Después de analizar los posibles datos de entrada, se considera emplear los siguientes datos:
Nombre/código de la asignatura: Se seleccionó este dato debido a que la asignatura como tal es una parte importante del porcentaje de aprobación.
Nombre/código del profesor: Se considera relevante debido a que los índices de aprobación dependen fuertemente del profesor que imparte las asignaturas.
Semestre de la asignatura: El semestre de la asignatura puede servir para identificar la complejidad del semestre, ya que es de conocimiento común que hay semestres que son más complicados que otros.
Carrera cursada: Se ha encontrado visualmente una tendencia importante en el índice de aprobación de ciertas asignaturas dependiendo de la carrera de los alumnos.
Año y período: Este dato de entrada se requiere para llevar la continuidad de las tendencias históricas de los índices de aprobación.
-
centaje de acreditación: El porcentaje de acreditación mostrado por los alumnos para un caso en particular (Nombre/código de la asignatura, Nombre/código del profesor, Semestre de la asignatura, Carrera cursada, Año y período).
Porcentaje de acreditación: El porcentaje de acreditación mostrado por los alumnos para un caso en particular (Nombre/código de la asignatura, Nombre/código del profesor, Semestre de la asignatura, Carrera cursada, Año y período).
Con estos datos se realizó la construcción de un registro de casos, sobre el cual se realizarán las operaciones necesarias para realizar el pronóstico por los modelos propuestos en este trabajo.
B. Promedios como modelo estadístico
Actualmente, este problema es resuelto asignando un porcentaje genérico de aprobación, el cual podría ser del 80%, 85% o algún otro valor. Sin embargo, para efectos de esta investigación se realizarán subdivisiones del total de las asignaturas para realizar promedios parciales, con el objetivo de permitir una mejor obtención de promedios por grupos y evitar los grandes errores porcentuales que podrían ocurrir al emplear un solo promedio global.
De tal forma que los datos mostrados anteriormente serán seccionados en 6 grupos de 89 elementos aproximadamente, para posteriormente evaluar el promedio del porcentaje de acreditación y calcular el porcentaje de error promedio con respecto de la media, el cual será mostrado en detalle en la Sección III.
C. Red neuronal como modelo causal
Las redes neuronales son una rama de la inteligencia artificial, estas son utilizadas en múltiples áreas del conocimiento y son utilizadas comúnmente como clasificadores, para aplicaciones de visión por computadora, como controladores o como mecanismos de pronóstico. Estas redes pretenden simular el comportamiento de neuronas biológicas a base de funciones matemáticas.
Una de las características más importantes de las redes neuronales es que son capaces de aprender a través de la experiencia, que también se puede apreciar como aprendizaje a partir de un conjunto de datos de entrenamiento.
El aprendizaje es el proceso mediante el cual la red neuronal ajusta sus conexiones para producir los resultados deseados. Como se mencionó anteriormente, una red neuronal simula el comportamiento de las neuronas biológicas y estas realizan su procesamiento basado en las conexiones que tienen entre ellas. De tal manera que el aprendizaje en una red neuronal artificial es el proceso por el cual las conexiones de la red neuronal son modificadas para responder apropiadamente a la información presentada.
Las redes neuronales han sido utilizadas satisfactoriamente para otros problemas relacionados con el pronóstico [6,7,8] tal es el caso del pronóstico de la demanda del turismo, cadenas de suministro, consumo de energía, y del pronóstico de cargas entre otros.
Una de las principales ventajas de las redes neuronales como modelos causales, es que pueden llegar a pronosticar datos de los que no se tiene información previa, como por ejemplo cuando un profesor imparte una asignatura que nunca había impartido. En estos casos, las redes neuronales utilizan la información aprendida de ese profesor, independiente de sus asignaturas, para proponer índices de aprobación aproximados.
III. Resultados
En este apartado se describen los resultados obtenidos de la comparación de un método estadístico y un método causal para el pronóstico de los porcentajes de aprobación de los alumnos. El método estadístico se realizó obteniendo el promedio del porcentaje de aprobación de los alumnos de los datos históricos del registro de casos, mientras que el método causal es implementado a través de una red neuronal de tipo perceptrón multicapa tomado de las librerías de WEKA.
A partir de esta experimentación se desea identificar el método de pronóstico que posea menor error para ser utilizado en el desarrollo final.
Las pruebas fueron realizadas con un reducido conjunto de datos (noventa y tres registros), el cual fue utilizado tanto para entrenamiento como para el pronóstico.
La comparación se llevó a cabo mediante el cálculo del MAPE (Min Average Porcentage Error) para las distintas pruebas realizadas a ambos modelos.
El MAPE se calculó empleando la ecuación (2):
Donde:
n = Cantidad de casos que se encuentran en el registro de casos (fin de la Sección 2.A).
P_Acri = Porcentaje de acreditación histórico del elemento i del registro de casos.
ValEstimadoi = Porcentaje de acreditación obtenido por el modelo empleado para el elemento i del registro de casos.
A. Modelo estadístico
Este modelo fue aplicado para seis secciones del registro de casos, para cada sección se calculó el promedio de la cantidad de aprobación de los alumnos para todos los casos de cada sección. Cada uno de los promedios calculados para cada una de las secciones es utilizado como ValEstimado para calcular el MAPE, el cual se muestra en la Tabla 1.
De acuerdo con estos resultados, se calculó el promedio, desviación estándar, valor máximo, valor mínimo listado en la Tabla 2.
B. Modelo causal
El uso de una red neuronal con una configuración aleatoria no se considera conveniente para el objetivo de nuestro trabajo. Es recomendable realizar un estudio de la configuración de los parámetros de la rede neuronal para tomar una decisión informada al respecto del mejor modelo a utilizar. Por lo que se realizó una selección de valores (Tabla 3) para distintos parámetros de la red neuronal.
Donde N = Cantidad de iteraciones, E = Errores antes de la detención, y, H = Configuración de las capas ocultas.
De forma natural, se producirían noventa configuraciones distintas para estos parámetros. Sin embargo, se utilizaron Covering Arrays de tamaño 2 para reducir el número de configuraciones a treinta [9]. En la Tabla 4 se muestran seis configuraciones representativas distribuidas uniformemente según el desempeño producido de menor a mayor MAPE.
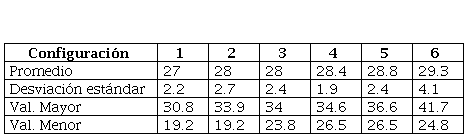
Para corroborar el desempeño de cada una de las configuraciones de los parámetros, se realizó el cálculo del MAPE para treinta ejecuciones (con semilla aleatoria) de cada una de las treinta configuraciones de parámetros generados por la técnica de covering arrays. Posteriormente se calculó el MAPE promedio, su desviación estándar, el valor máximo y mínimo para cada configuración de parámetros y de esta manera se obtuvieron las seis configuraciones representativas mostradas en la Tabla 4. La Tabla 5 contiene el MAPE promedio, la desviación estándar el máximo valor y el menor de las treinta ejecuciones del entrenamiento.
IV. Discusión
De acuerdo con los resultados obtenidos de la comparación del modelo estadístico y el modelo causal para el pronóstico de los porcentajes de aprobación de los alumnos, se puede considerar que el modelo causal produce resultados más consistentes (de 27 a 29.3) que el modelo estadístico (de 26.48 a 77.18).
Sin embargo, una prueba no paramétrica de Mann-Whitney aplicada a ambos conjuntos de datos arroja un p-value de 0.335 que es mayor a un valor de alpha de 0.05, lo cual indica que no se considera que ambos métodos sean estadísticamente diferentes.
Por otra parte, se considera que el resultado de la prueba estadística puede ser debido que el conjunto de elementos comparados es pequeño, solamente de seis elementos, y para obtener un resultado que indique una diferencia significativa se requeriría que uno de los métodos mejore al otro para prácticamente todos los casos.
V. Conclusiones
En este trabajo se pretende realizar un estudio para identificar el mejor método para realizar pronósticos de los índices de aprobación de los alumnos para predecir la demanda de asignaturas para el siguiente período académico. Los resultados muestran que el modelo causal produce mejores resultados en promedio y más consistentemente que el modelo estadístico. Sin embargo, las pruebas estadísticas indican que no hay una diferencia significativa entre ambos modelos. Se considera como parte de un trabajo futuro, realizar una mayor cantidad de pruebas para volver a realizar este estudio estadístico y obtener mayor precisión en los resultados.
Con la intención de identificar la existencia de algún otro modelo causal que produzca un menor porcentaje de error que las redes neuronales de retropropagación, se plantea como trabajo futuro el análisis de otras redes neuronales o máquinas de soporte vectorial como posibles alternativas de modelo causal. Adicionalmente se considera realizar pruebas con un registro de casos de mayor tamaño para las pruebas finales.
Contribución de los autores
Jesús David Terán Villanueva, Salvador Ibarra Martínez, Julio Laria Menchaca realizaron las secciones de propuesta de solución, redes neuronales como modelo causal, datos de entrenamiento, resultados del modelo causal y parte de las conclusiones.
José A. Castán Rocha y Alejandro Humberto García-Ruiz realizaron pruebas del modelo estadístico y el contenido de la sección de discusión y parte de conclusiones.
José Eduardo Martínez Infante y Mayra Guadalupe Treviño Berrones realizaron contenido de la introducción y cálculo del pronóstico de la demanda.